Y a ti, ¿cómo te llamamos?
Recientemente se ha descubierto un nuevo mineral cerca de Moaña, un municipio localizado en la provincia de Pontevedra, que ha recibido el nombre de ermeloita.
 Muestra del nuevo mineral ermeloita siendo analizada en los laboratorios de la Universidad de Santiago de Compostela (USC). Fuente: USC.
Muestra del nuevo mineral ermeloita siendo analizada en los laboratorios de la Universidad de Santiago de Compostela (USC). Fuente: USC.Si habéis intentado pronunciar dicho nombre en voz alta un par de veces seguidas, es probable que se os haya trabado un poco la lengua y estéis pensando ahora mismo: Pero, ¿cómo se les ha ocurrido ponerle ese nombre tan raro?
Esta pregunta nos la podríamos hacer para todos y cada uno de los minerales que conocemos hoy en día. Y es a la que voy a tratar de dar respuesta en este artículo.
Aunque no lo creáis, hay un organismo internacional que se encarga de vigilar tanto la nomenclatura como la correcta clasificación sistemática de los minerales de todo el mundo, la Commission on New Minerals, Nomenclature and Classification (CNMNC) of the International Mineralogical Association (IMA). O, en castellano, la Comisión de Nuevos Minerales, su Nomenclatura y Clasificación de la Asociación Mineralógica Internacional. Vamos, que si descubrimos un mineral desconocido por la ciencia hasta ese momento y queremos ponerle un nombre, tenemos que seguir sus reglas.
Y es entonces cuando tenemos dos caminos que podemos seguir a la hora de elegir dicho nombre. O bien lo hacemos de una manera más formal y aludimos a alguna propiedad o característica de ese nuevo mineral, tales como su composición química o su color, o nos convertimos en espíritus libres y le damos una denominación que no nos aporta ninguna información propia del mineral.
 Venas de calcita (color blanco) recristalizadas en una baldosa de la roca ornamental “Negro Markina” empleada en un soportal de Bilbao. Fuente: Blanca María Martínez
Venas de calcita (color blanco) recristalizadas en una baldosa de la roca ornamental “Negro Markina” empleada en un soportal de Bilbao. Fuente: Blanca María MartínezComo ejemplos de nombres más formales e informativos, podemos encontrarnos con la calcita, llamada así porque tiene calcio en su composición, o la magnesita, que incluye el magnesio. Y seguro que os suenan la cianita, que es de un color azul brillante, y el oropimente, que presenta un color amarillento dorado.
Pero es por la vía más informal de nomenclatura donde aparecen los nombres de minerales más curiosos e, incluso, divertidos.
Es aquí donde podemos incluir el granate. Puede que penséis que me he confundido al no ponerlo junto a la cianita y el oropimente creyendo que su nombre procede del color rojo oscuro al que conocemos, precisamente, como granate, pero es que el origen de su nombre es muy particular. El granate mineral se denomina así porque recuerda a las semillas, o granos, de la granada, la fruta del árbol conocido como granado.
 Muestra de goethita exhibida en el “Paseo Geológico de Bizkaia”, situado en el Arboretum del Campus de Leioa de la Universidad del País Vasco UPV-EHU. Fotografía de Ana Pascual (Departamento de Geología, UPV-EHU)
Muestra de goethita exhibida en el “Paseo Geológico de Bizkaia”, situado en el Arboretum del Campus de Leioa de la Universidad del País Vasco UPV-EHU. Fotografía de Ana Pascual (Departamento de Geología, UPV-EHU)Un segundo grupo de nombres hace mención o sirve como homenaje a personas famosas, no siempre relacionadas con la Geología o la Mineralogía. Como ejemplos tenemos la goethita, dedicada al filósofo alemán Johann Wolfgang von Goethe. O la livingstonita, nombrada en honor al explorador escocés David Livingstone, al que Stanley saludó con su famosa frase “el doctor Livingstone, supongo” cuando lo encontró en el corazón de África. O la smithsonita, llamada así en homenaje a James Smithson, el mineralogista inglés con cuya herencia se fundó la Institución Smithsonian.
Y hay un tercer grupo de nombres que se refieren a localidades geográficas. Entre ellos nos encontramos con la jarosita, cuya nomenclatura se refiere al Barranco Jaroso, situado en la Sierra Almagrera, provincia de Almería. También tenemos el aragonito, que hace alusión a Molina de Aragón, localidad de la provincia de Guadalajara y que se ha elegido como imagen central del logotipo del Geoparque Mundial Unesco de Molina de Aragón-Alto Tajo. O la villamaninita, que se refiere a Villamanín, villa de la provincia de León.
Pues es en este último grupo donde también podemos incluir al nuevo mineral ermeloita, ya que su nombre procede de la zona donde se ha descubierto, el Monte Ermelo.
Aquí solo os he puesto unos pocos ejemplos, pero hay miles de minerales descubiertos hasta la fecha con los que podéis pasar un buen rato buscando el origen de sus nombres. Algunos son muy, pero que muy curiosos.
Referencia:
Zaragoza Vérez, G., Rodríguez Vázquez, C. J., Fernández Cereijo, I., González del Tánago, J., Jiménez Martínez, R., Dacuña Mariño, B., Barreiro Pérez, R., Vázquez Fernández, E., Gómez Dopazo, M., and Lantes-Suárez, O. (2022). Ermeloite, IMA 2021-017a, in: CNMNC Newsletter 68, Eur. J. Mineral., 34, doi: 10.5194/ejm-34-385-2022.
Para saber más:
Introducción histórica a la mineralogía
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo Y a ti, ¿cómo te llamamos? se ha escrito en Cuaderno de Cultura Científica.
Alison Hartcourt y Ailsa Land, dos matemáticas unidas por la programación lineal
Alison Hartcourt yAilsa Land definieron en 1960 un algoritmo para resolver problemas de programación discreta. El influyente artículo en el que introdujeron este algoritmo ha tenido un enorme impacto en la literatura académica y en la resolución práctica de problemas económicos y sociales. Muchas personas desconocen que dos mujeres son las autoras de ese trabajo: ellas ocultaron deliberadamente sus nombres.
 Fuente: Jstor
Fuente: JstorAlison Hartcourt (1929)
“La estadística es números con contexto, y el contexto siempre ha sido importante para mí”.
 Alison Harcourt. Fuente: U. de Melbourne.
Alison Harcourt. Fuente: U. de Melbourne.
Alison Doignació el 24 de noviembre de 1929 en Colac (Victoria, Australia). Su madre, Louie Grant, y su padre, el médico Keith Doig, eran de ascendencia escocesa. Tenía una hermana y dos hermanos.
Tras su educación escolar, Alison se matriculó en la Universidad de Melbourne, donde obtuvo un bachillerato universitario en letras con mención en matemáticas y, posteriormente, un bachillerato universitario en ciencias con mención en física. Como muestra de sus habilidades científicas, mientras realizaba un máster para especializarse en estadística, desarrolló una técnica para la programación lineal entera.
Precisamente gracias a sus conocimientos en programación lineal, a finales de los años 1950 comenzó a trabajar en el London School of Economics (LSE). En 1960, junto a Ailsa Land, publicó un artículo histórico en la revista Econometrica en el que describía un algoritmo de optimización de ramificación y poda para resolver problemas NP-complejos. Este algoritmo tiene aplicaciones en diversos campos, que van desde la logística de transporte hasta la optimización del ángulo del haz de partículas en los tratamientos por radioterapia. Las dos investigadoras publicaron el artículo escondiendo sus nombres, tan solo con sus iniciales, para evitar que su trabajo fuera considerado “de segunda” por el hecho de ser mujeres.
En 1963, Doig regresó a Australia, siendo contratada como profesora titular de estadística en la Universidad de Melbourne.
A mediados de la década de 1960 se unió al equipo liderado por el sociólogo Ronald Henderson (1917-1994) que intentaba cuantificar el alcance de la pobreza en Australia. Este grupo desarrolló en 1973 la llamada Línea de Pobreza Henderson, el ingreso mínimo requerido para cubrir las necesidades básicas de una familia formada por dos adultos y dos niños. Las técnicas desarrolladas por el equipo de Henderson han sido utilizadas desde 1979 por el Instituto de Investigación Económica y Social Aplicada de Melbourne para actualizar regularmente el umbral de pobreza en Australia.
En 1970, Alison pidió una licencia de estudios para viajar a Suecia, donde fue coautora de dos artículos sobre química teórica junto a su marido, el químico Richard Harcourt, con el que se había casado en 1968 y con el que tuvo dos hijos.
En 1975, tras la destitución del Primer ministro de Australia, el laborista Gough Whitlam, Alison Harcourt y el estadístico Malcolm Clark notaron irregularidades en la distribución del orden de los partidos en las papeletas electorales del Senado para las elecciones federales de 1975. Lo descubrieron al observar que, en todos los estados, los partidos de la coalición ocupaban siempre una de las dos primeras posiciones.
Harcourt y Clark presentaron un informe al Comité Selecto Conjunto sobre la Reforma Electoral, dosier que en 1984 terminó en una enmienda a la Ley Electoral de la Commonwealth para introducir un nuevo método de asignación aleatoria doble a la hora de establecer las posiciones de los partidos políticos en las papeletas de votación. Este sistema todavía se usa en la actualidad. Harcourt y Clark publicaron un artículo sobre su estudio, con recomendaciones, en 1991.
Harcourt se jubiló en 1994, aunque continuó como asesora estadística durante varios años.
Entre otros muchos reconocimientos, en junio de 2019, Alison Harcourt fue nombrada Oficial de la Orden de Australia en reconocimiento a “su servicio distinguido a las matemáticas y la informática a través de la investigación pionera y el desarrollo de la programación lineal entera”.
Ailsa Horton Land (1927-2021)“Optamos por presentarlo [el artículo] solo con nuestras iniciales y apellidos de manera deliberada. Una elección que no creo que parezca apropiada hoy en día”.
 Ailsa Land. Fuente: Wikimedia Commons.
Ailsa Land. Fuente: Wikimedia Commons.
Ailsa Dicken nació el 14 de junio de 1927 en West Bromwich (Staffordshire, Inglaterra). Era la única hija de Elizabeth Greig y Harold Dicken.
Ailsa tenía un gran interés por la ciencia, pero tuvo malos resultados en la escuela primaria local por motivos de disciplina. Su familia decidió entonces enviarla a un pequeño internado mixto en Hastings durante un año. Este centro escolar tenía un enfoque especial en matemáticas, y su cincuentena de estudiantes trabajaba a su propio ritmo.
Cuando estalló la Segunda Guerra Mundial, Ailsa y su madre emigraron a Canadá para pasar una guerra más tranquila en casa de unos parientes. El padre fue llamado a filas y no pudo reunirse con ellas.
Tras tres años en Toronto, en 1943, Ailsa y su madre decidieron unirse al Cuerpo del Ejército de Mujeres Canadienses; Ailsa mintió sobre su edad para ser admitida. En 1944, las dos colaboraban en trabajos administrativos en el Cuartel General de la Defensa Nacional en Ottawa, una unidad compuesta únicamente por personal femenino que reemplazaba a los hombres enviados a Inglaterra para apoyar al ejército aliado.
Tras finalizar la guerra, en 1946, ya en Inglaterra, Ailsa ingresó en la LSE para estudiar una licenciatura en economía; como militar desmovilizada tuvo preferencia en el acceso y consiguió una beca. Durante su primer año ganó el premio Bowley por un artículo de estadística aplicada a la economía. Tras graduarse en 1950, pasó el resto de su carrera en esta institución, siendo la primera profesora de investigación operativa de Gran Bretaña.
En 1956 defendió su tesis doctoral bajo la supervisión de George Morton, con un trabajo que aplicaba técnicas de programación lineal al transporte de carbón.
Y, como hemos comentado antes, trabajó junto a Alison Doig en ese novedoso método de optimización que fue patrocinado por la empresa British Petroleum; la compañía deseaba mejorar los modelos de programación lineal existentes para las operaciones de refinería. Las dos matemáticas carecían de ordenador para realizar su tarea, pero desarrollaron un algoritmo que el personal de la empresa pudo convertir posteriormente a Fortran.
A finales de la década de 1950, Ailsa Land también trabajó con la economista Helen Makower y George Morton en una serie de problemas de programación entera, entre los cuales se encontraba el conocido problema del viajante, que es precisamente un problema NP-complejo.
Ailsa también trabajó en el desarrollo de herramientas computacionales; en 1973 publicó con Susan Powell el libro Fortran Codes for Mathematical Programming: Linear, Quadratic and Discrete.
En 1953 se casó con el especialista en sistemas de información Frank Land, también profesor de la LSE, con quien tuvo dos hijas y un hijo.
En 1994 recibió el Premio Harold Larnder de la Sociedad Canadiense de Investigación Operativa por sus aportaciones en esta área. Y, en 2019, la Sociedad de Investigación Operativa le otorgó la Medalla Beale.
El Premio Ailsa Land de la LSE se otorga cada año en su honor al estudiante más destacado en el Máster de Investigación y Análisis de Operaciones.
Alisa Land falleció el 16 de mayo de 2021, a los 93 años.
Bonus
“Sigan adelante, mujeres en matemáticas. Sigan adelante, mujeres en todas las materias STEM”.
Con este inspirador alegato de Alison Hartcourt finaliza el siguiente video producido en 2019. Sin duda, con modelos como ella y Ailsa Land, es más fácil seguir adelante.
Referencias
-
Val Silberberg, Richard and Alison Harcourt, Profile, February-March 2019, 4-5.
-
Lauren Day, ‘I’ve always loved numbers’: Meet the ground-breaking grandmother of Australian mathematics, ABC News, 8 octubre 2018.
-
Alison Harcourt, The University of Melbourne
-
Alison Hartcourt, Wikipedia
-
Ailsa H. Land, The Institute for Operations Research and the Management Sciences
-
Ailsa Land, Wikipedia
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Alison Hartcourt y Ailsa Land, dos matemáticas unidas por la programación lineal se ha escrito en Cuaderno de Cultura Científica.
Einstein y Robert Millikan
Robert Millikan fue uno de los científicos más famosos de su época. Ganó el premio Nobel de física en 1923 por la medición de la carga del electrón y por el trabajo experimental que confirmó la teoría de Einstein de que la luz estaba constituida por partículas. Irónicamente, la intención de Millikan era demostrar que la teoría era falsa, e insistió durante años en que su trabajo confirmaba simplemente que las teorías de Einstein eran valiosas herramientas matemáticas, pero solo eso, no que probase la existencia de los fotones.
 Robert Millikan y Albert Eisntein en el Instituto de Tecnología de California en 1932. Fuente: Wikimedia Commons
Robert Millikan y Albert Eisntein en el Instituto de Tecnología de California en 1932. Fuente: Wikimedia CommonsEn 1896, Millikan fue contratado por la Universidad de Chicago, y estaba todavía allí en 1905 cuando Einstein publicó un artículo en el que afirmaba que la única manera de explicar cómo la luz cede energía a los electrones es asumiendo que la luz está compuesta de partículas, de forma análoga a la corriente eléctrica. Einstein encontró que la energía de una partícula de luz es igual a su frecuencia multiplicada por una constante, h, que terminó llamándose constante de Planck. Millikan ya tenía una reputación de gran experimentador, tras haber sido capaz de medir la carga del electrón, demostrando así que los electrones eran realmente entes físicos con propiedades consistentes, y que la electricidad es un fenómeno atómico. Pero solo porque aceptase que los electrones eran partículas no significaba que creyese que la luz podía ser algo parecido. Millikan conocía muy bien los experimentos en los que se demostraba que la interacción de dos rayos de luz tenía como resultado lo que uno podía esperar si fuesen ondas. Los científicos llevaban 50 años convencidos de que la luz era una onda, y Millikan era uno de ellos. Por lo que se dispuso a demostrar que la teoría de Einstein era errónea.
El experimento de Millikan medía la energía de los electrones que eran emitidos por una placa sobre la que incidía un rayo de luz. Sin embargo, para su sorpresa, los resultados parecían confirmar la teoría de Einstein de la naturaleza corpuscular de la luz. No solo eso, el experimento permitió la determinación más precisa hasta la fecha del valor de la constante de Planck. Décadas más tarde, cuando Millikan describía su trabajo, todavía asomaba un punto de frustración: “Empleé diez años de mi vida comprobando la teoría de Einstein de 1905 y, en contra de todas mis expectativas, me vi forzado a afirmar su verificación sin ambages a pesar de lo irrazonable que era”.
Con todo, Millikan todavía no aceptaba que su experimento probase que la luz estuviese compuesta por cuantos; solo admitiría que las matemáticas de Einstein correspondían con sus experimentos. En su artículo sobre el efecto fotoeléctrico, Millikan escribió: “la ecuación fotoeléctrica de Einstein […] parece que predice exactamente en todos los casos los resultados observados […] Sin embargo, la teoría semicorpuscular [sic.] por la que Einstein llegó a su ecuación parece actualmente completamente insostenible”. Millikan también describió la teoría de Einstein sobre las partículas de luz como una “hipótesis atrevida, por no llamarla insensata”. Millikan era consciente de que sin las ecuaciones de Einstein no se podía explicar el fenómeno de la fotoelectricidad usando el punto de vista clásico sobre la luz, por lo que sabía que algo tenía que cambiar, pero la introducción arbitraria de los fotones no era, para su gusto, la respuesta. Además Millikan trabajaba con Michelson (su director de tesis), que creyó toda su vida en la existencia de un éter a través del que las ondas de luz viajaban (a pesar de que sus propios experimentos demostraban su no existencia), por lo que se reforzaban mutuamente en su creencia en la naturaleza ondulatoria de la luz como la única posible.
Mientras la comunidad científica seguía estos desarrollos, en 1919 Einstein y Millikan aparecieron mencionados juntos en la prensa popular. Ese noviembre se hizo público que las observaciones astronómicas del eclipse solar de ese año confirmaban la teoría general de la relatividad de Einstein, lo que le dio fama instantánea y motivó una serie de artículos en el The New York Times. En alguno de ellos aparecía un Einstein altanero que afirmaba que sólo doce personas en el mundo comprendían su teoría. Días después de esto hubo, como era de esperar, una reacción furibunda, y un editorial del propio periódico, del 13 de noviembre, decía: “La gente que se ha sentido un poco molesta porque se les ha dicho que no podrían entender la nueva teoría, ni siquiera si se les explicase con todo cuidado y amabilidad, sentirán alguna clase de satisfacción al saber que la solidez de la deducción de Einstein ha sido puesta en cuestión por R.A. Millikan”.
A pesar de todo, mientras Millikan continuaba negando la existencia de los fotones, su “confirmación” fue un factor que ayudó a que Einstein recibiese el premio Nobel en 1921. En 1923, Millikan recibiría él mismo el premio “por su trabajo sobre la carga elemental de la electricidad y sobre el efecto fotoeléctrico”. En su conferencia con motivo de la recepción del premio, sin embargo, Millikan volvió a mencionar que “el concepto de cuantos de luz localizados a partir del cual Einstein consiguió su ecuación debe ser considerado aún como lejos de estar establecido”.
Nunca hubo, sin embargo, animosidad personal entre los dos científicos, y se respetaban muchísimo el uno al otro. En 1921, Millikan aceptó un trabajo en lo que llegaría a llamarse Instituto de Tecnología de California (Caltech), y se dispuso a convertirlo en una institución puntera en investigación. Millikan ofreció a Einstein un puesto en el Caltech en 1923, pero el físico alemán lo rechazó. Einstein sí aceptó una invitación a visitar los Estados Unidos y Millikan actuó como su anfitrión. Finalmente (y todavía no está muy claro por qué, aunque puede que influyese el creciente antisemitismo en Alemania), en 1931 Einstein aceptó un puesto para enseñar a tiempo parcial en el Caltech.
En 1950, a los 82 años, Millikan escribió su autobiografía. Para entonces toda la comunidad científica había aceptado la existencia de los fotones, incluido Millikan. En el libro, Millikan no menciona que tardó décadas en aceptar las teorías de Einstein. Probablemente nunca sabremos si lo que Millikan contaba era realmente cómo recordaba los acontecimientos o fue la vanidad la que venció y se negó a reconocer lo que claramente había sido un error.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Una versión anterior de este artículo se publicó en Experientia Docet el 22 de nombre de 2009.
El artículo Einstein y Robert Millikan se ha escrito en Cuaderno de Cultura Científica.
¿Por qué el estómago no se digiere a sí mismo? Bueno, a veces, sí lo hace
 Imagen de Robystarm en Pixabay
Imagen de Robystarm en PixabayEl jugo gástrico es una solución extremadamente ácida. Su pH normal se encuentra entre 1,5 y 3, lo que significa que es más ácido que el vinagre y está más o menos al mismo nivel que el zumo de limón. Este pH tan bajo se debe al ácido clorhídrico (HCl) que liberan las células parietales, situadas en la pared del estómago. El HCl, más conocido como salfumán, tiene multitud aplicaciones en la vida diaria, desde productos de limpieza para el hogar hasta infinidad de usos industriales (para desatascar, desincrustar, fabricar diferentes materiales…).
Cada día, se producen en torno a 1,5-2,5 litros de jugo gástrico (compuesto principalmente por agua, HCl, enzimas digestivas y electrolitos), esencial para la digestión de los alimentos y para prevenir infecciones por diferentes agentes patógenos. ¿Cómo es posible que el estómago se libre de los efectos corrosivos del jugo gástrico, si resulta tan ácido? A grandes rasgos, intervienen cuatro elementos defensivos que protegen a este depósito muscular de ser víctima de sus propios fluidos. En primer lugar, la superficie interna del estómago está recubierta por una espesa y viscosa capa de moco alcalino gracias a la presencia de bicarbonato, Este moco actúa como una barrera tanto física como química que protege al estómago de su propio jugo y permite que en su superficie interna se dé un pH prácticamente neutro (7).
Si vamos más allá de la capa de moco, las células que recubren la superficie interna del estómago, las células epiteliales, están unidas entre sí de forma hermética a través de un complejo entramado de proteínas. Esta barrera física es muy compacta e impide el paso del jugo gástrico entre las células gástricas, lo que sería un grave problema porque provocaría la digestión del tejido más profundo del estómago.
Además de los mecanismos anteriores, las células epiteliales se renuevan constantemente a lo largo de la vida para garantizar la protección del estómago. Estas células tienen una vida media de tan solo 3-6 días, lo que implica que cada minuto que pasa se eliminan en torno a 500.000 células epiteliales que van a parar al jugo gástrico. Por último, la secreción del ácido en el estómago está regulada con suma precisión para que la acidez nunca sea excesiva en este órgano y que esta dependa, sobre todo, de la ingesta de alimentos. De ello se encargan tanto el sistema nervioso simpático y parasimpático como las hormonas gastrina, histamina, somatostatina y acetilcolina.
Por supuesto, en condiciones normales, estas cuatro medidas de protección del estómago funcionan a la perfección y no llegamos a ser conscientes de que tenemos un depósito de ácido en nuestro interior. Sin embargo, multitud de factores pueden alterar el delicado equilibrio entre los elementos protectores gástricos y el corrosivo jugo. El consumo excesivo de alcohol, la ingesta frecuente de ciertos fármacos (como los antiinflamatorios no esteroideos) o la bacteria Helicobacter pylori (que sobrevive en el medio ácido gracias a la liberación de amoníaco), entre otras muchas causas, pueden lesionar la mucosa del estómago y hacer que sufra daños por su contenido ácido. Cuando este fenómeno ocurre hablamos de úlceras pépticas: llagas que provocan un dolor sordo o ardor en la zona del estómago, que se acentúa entre comidas.
¿Qué hacemos entonces para curar las úlceras, en las que el ácido del jugo gástrico está «digiriendo» una zona del estómago? En primer lugar, lo primero es tratar la causa que ha desbaratado el delicado equilibrio en el estómago. Por ejemplo: antibióticos contra H. pylori, sustitución de medicamentos que provocan daño en la mucosa gástrica por otros que no lo hagan, abstinencia de alcohol….
Además, también hay que atenuar la liberación de HCl en el estómago, para disminuir la acidez y así dar tiempo al estómago para que se cure así mismo (por suerte, la mucosa es un portento en renovarse a sí misma). Esto lo conseguimos con los medicamentos llamados inhibidores de la bomba de protones. Entre ellos, el más popular es el omeprazol. Se conocen (mal) como «protectores gástricos», aunque en realidad lo que hacen es disminuir el ácido del estómago al bloquear los canales de las células parietales que producen el HCl.
Hoy en día, gracias a estos fármacos, el pronóstico de las úlceras es excelente. Es muy raro que una úlcera péptica evolucione y llegue a atravesar la pared del estómago, provocando la perforación de este órgano. Esto supondría una emergencia médica de gran riesgo para la vida, porque la liberación del jugo gástrico a las zonas colindantes del estómago provocaría graves daños en el cuerpo humano. Por suerte, casos así son excepcionales.
Para saber más:
El estómago (u órgano equivalente)
H. pylori crea túneles en la mucosa del estómago
Sobre la autora: Esther Samper (Shora) es médica, doctora en Ingeniería Tisular Cardiovascular y divulgadora científica
El artículo ¿Por qué el estómago no se digiere a sí mismo? Bueno, a veces, sí lo hace se ha escrito en Cuaderno de Cultura Científica.
El afinador de Eratóstenes
José Manuel González Gamarro
La historia de la música de occidente se caracteriza por una gran riqueza de textos musicales, tanto de partituras como de libros analizando sus características y propiedades. Analizando los textos se puede saber cómo era la música de hace, por ejemplo, 500 años, no solo tocando la partitura, sino leyendo sobre cómo eran los instrumentos, la manera de componer o en qué contexto se escuchaba. Huelga decir que la música de hace cientos de años era muy diferente a la que se compone en la actualidad, ha ido transformándose, tanto en su forma como en su contenido. Una de las cosas que más ha variado a lo largo de la historia es la afinación. La palabra «afinación» tiene aquí una connotación muy amplia, pues no solo se refiere a cómo se templaban los instrumentos musicales, sino a cómo se concebían las consonancias y disonancias. Esto atañe también a la manera de cantar y a la percepción del oyente de cada época, es decir, hubo sistemas de afinación (incluso se daban con simultaneidad en el tiempo) que decidían lo que sonaba bien o mal, la delgada línea entre lo prohibido y lo permitido. Hay que tener en cuenta que la forma de concebir la afinación musical también ha variado a lo largo del tiempo, desde la mera comparativa hasta la estandarización de las vibraciones por segundo que le corresponde a cada nota.
La afinación pitagóricaUna de las afinaciones más usadas y de las que más literatura ha generado es la afinación pitagórica. Más allá de las leyendas e historias que se han ido difundiendo a lo largo de los años gracias a filósofos como Boecio, a la figura de Pitágoras se le atribuyen descubrimientos musicales en relación con las matemáticas que implican el inicio de la ciencia armónica.1 Estos descubrimientos, a través supuestamente de experimentos con vasos de agua, pesos o flautas, se ejemplifican claramente en el monocordio. Este instrumento se compone de una sola cuerda y una regla numerada. Las consonancias se calculan según la parte de la cuerda que vibra. Teniendo en cuenta que la tensión de la cuerda es constante, si se divide justo a la mitad, el intervalo entre el sonido que produce la cuerda sin dividir y el sonido de la mitad de la cuerda es de una octava, es decir, la razón es 2/1. En otras palabras, si la nota de esa cuerda es, por ejemplo, un Do, al hacer vibrar solo la mitad de la cuerda volverá a sonar otro Do, pero una octava más aguda. Esto es solo un ejemplo puesto que el nombre de las notas como tal no se establecería hasta bastantes siglos después. Este intervalo de octava y esta proporción es la que se ha intentado mantener constante a lo largo de la historia y los diferentes sistemas de afinaciones. Pitágoras también definió los intervalos de quinta con la razón 3/2 (dividir la cuerda en tres partes iguales y hacer sonar dos) y el intervalo de cuarta con la razón 4/3. Según Arístides Quintiliano en su De Musica, el matemático recomendaba encarecidamente usar el monocordio para poder desechar la apreciación sensorial, es decir, decidir cuando existe consonancia mediante la apreciación intelectual, con puro cálculo numérico. Teniendo en cuenta que para sumar intervalos se multiplican sus razones y para restarlos se dividen, se pueden calcular los demás intervalos. Por ejemplo, el tono (una supuesta distancia aproximada entre Do y Re) es la diferencia entre la quinta y la cuarta y se calcula de la siguiente manera: 3/2 : 4/3 = 9/8. La diferencia entre la cuerda «al aire» y el sonido producido por la razón 9/8 es un tono.
Con el devenir de la historia, la música y los instrumentos musicales fueron ganando en complejidad. Además, para los pitagóricos las consonancias eran la cuarta, la quinta, la octava, la doble octava y la octava más la quinta. Todos los demás intervalos había que calcularlos en función de estos. Una consecuencia es la especulación matemática acorde con la musical, ya que, excepto la octava, ninguna consonancia puede dividirse en dos partes iguales, además tampoco se pueden sumar consonancias iguales para obtener otra consonancia. La suma de dos cuartas, por ejemplo, da como resultado una séptima, que no era una consonancia. El problema principal viene cuando queremos realizar una escala, es decir, una sucesión de tonos hasta llegar a la octava. Seis tonos (9/8) sucesivos sobrepasan la octava, no se llega exactamente al mismo sonido. Hay una pequeña diferencia llamada comma pitagórica. Esta diferencia son 24 cents si escogemos esta unidad logarítmica para medir intervalos. No es algo desdeñable ya que un oído fino puede apreciar una diferencia de 3 cents. Este «pequeño» desajuste ha provocado diferentes sistemas de afinación que se han ido adaptando a la transformación de la música y los cambios en la concepción de los intervalos permitidos o consonantes. Ha habido sistemas de afinación circulares, que vuelven al mismo sonido (como el nuestro de la música occidental), repartiendo ese desajuste entre las notas de la escala, así como otros sistemas irregulares. De hecho, según Murray Barbour2 ha habido más de 180 sistemas de afinación a lo largo de nuestra historia.
 Ilustración 1. Dibujo de un círculo de terceras en una escala de 31 notas. Elementa musica, Quirimus van Blakenburg, 1739. Fuente: Goldaraz Gaínza, 1998.
Ilustración 1. Dibujo de un círculo de terceras en una escala de 31 notas. Elementa musica, Quirimus van Blakenburg, 1739. Fuente: Goldaraz Gaínza, 1998.
Toda esta complejidad tiene como consecuencia la creación de diferentes escalas y de diferentes instrumentos adaptados a estas escalas. Nuestra escala tiene siete notas (Do-Re-Mi-Fa-Sol-La-Si) que si las dividimos en semitonos iguales nos da la escala cromática de doce. Este es el límite de nuestra escala occidental. Sin embargo, a lo largo de la historia, debido a estos diferentes sistemas de afinación, han existido escalas de 31 o incluso de más de 50 sonidos diferentes. Para ello también se idearon instrumentos musicales acordes a las dificultades de la afinación, como el denominado Sambuca Lincea de los músicos Fabio Colonna o Scipione Stella con seis teclados en el mismo instrumento. Todo un desafío para los músicos de hoy en día.
 Teclado de la Sambuca Lincea de F. Colonna, 1618. Fuente: Goldaraz Gaínza, 1998. El mesolabio de Eratóstenes
Teclado de la Sambuca Lincea de F. Colonna, 1618. Fuente: Goldaraz Gaínza, 1998. El mesolabio de Eratóstenes
La supuesta insistencia de Pitágoras en evitar la apreciación sensorial deja insuficiente a la aritmética a medida que transcurre el tiempo debido a que, ya no solo hay que calcular quintas o cuartas, sino tonos y partes de comma. Esto último implicaría hallar medios, tercios, cuartos, etc. de esta distancia de 24 cents mediante sus razones por lo que habría que hallar la raíz cuadrada, cúbica, cuarta, etc. de la razón 81/80, dando cantidades irracionales. Esto propició la búsqueda de otras soluciones para algunos sistemas de afinación basadas en la geometría. Una de estas soluciones es utilizar un instrumento creado por Eratóstenes de Cirene (276-194 a. C.), el mesolabio. Esta especie de ábaco se compone de tres paralelogramos rectangulares que se mueven a lo largo de unas estrías, superponiéndose unos a otros. Se usa para hallar medias y proporciones y uno de sus primeros usos fue la duplicación del volumen de un cubo, como se explica en este vídeo, pudiéndose ver su funcionamiento a partir del minuto 10:00. Aunque el cálculo pueda parecer en un principio aproximado puesto que se trata de buscar los puntos de intersección, su uso evita las complicadas operaciones matemáticas que supone hallar distancias tan pequeñas. Moviendo rectángulos con diagonales trazadas y uniendo puntos con líneas rectas en las intersecciones, se calculan dos medias proporcionales en una razón superparticular, es decir, la razón de dos números enteros consecutivos. Esto encaja como anillo al dedo en las razones usadas en la música. Es un aparato que se usa muchos años después de su invención para el cometido de la afinación. Los músicos Gioseffo Zarlino y Pedro Salinas lo usarán y dejarán constancia de ello en sus tratados.
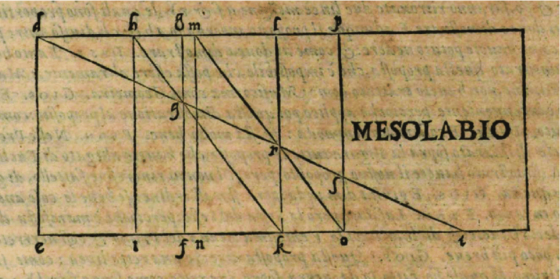 Dibujo del mesolabio en Dimostrationi Harmoniche, G. Zarlino, 1571.
Dibujo del mesolabio en Dimostrationi Harmoniche, G. Zarlino, 1571.
Aunque el cometido del mesolabio era encontrar dos medias, Zarlino indica que puede usarse para cualquier número de medias si se aumenta el número de paralelogramos. De hecho, este músico ilustra la división del mástil de un laúd mediante el mesolabio en el temperamento igual, doce partes iguales. También Pedro Salinas hace uso del añadido de paralelogramos para aumentar el número de medias, sin embargo, otros teóricos como el matemático Marin Mersenne sostienen que solo es posible su uso para dos medias.
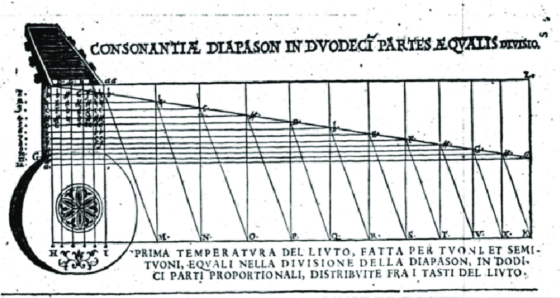 Explicación del uso del mesolabio, Sopplimenti musicali, G. Zarlino, 1588.
Explicación del uso del mesolabio, Sopplimenti musicali, G. Zarlino, 1588.Sea como fuere, Eratóstenes ideó un aparato que tuvo un uso muy prolongado en el tiempo y alejado de su primer cometido, otorgando una solución práctica a problemas que no existían en el tiempo en el que se concibió. Aunque su más conocida hazaña fue calcular la circunferencia de la Tierra, también fue capaz de inventar una especie de calculadora con un mecanismo muy sencillo y que fue muy significativo para el desarrollo de algunos sistemas de afinación de la música occidental. Este matemático que fue director de la Biblioteca de Alejandría tiene un papel primordial en la historia de esta disciplina, así como en la astronomía y la geografía, pero, aunque más discreto, también tiene un pequeño hueco en la historia de nuestra música.
Referencias:
1 Goldaraz Gaínza, J. Javier. Afinación y temperamento en la música occidental. Alianza, 1998
2 Barbour, J. M. Tuning and Temperament, a Historical Survey. Da Capo Press, 1972.
Sobre el autor: José Manuel González Gamarro es profesor de guitarra e investigador para la Asociación para el Estudio de la Guitarra del Real Conservatorio Superior de Música “Victoria Eugenia” de Granada.
El artículo El afinador de Eratóstenes se ha escrito en Cuaderno de Cultura Científica.
CienciaClip 2020 – Lo que verías al viajar a la velocidad de la luz

Ciencia Clip es un concurso de vídeos divulgativos de ciencia diseñados, producidos y protagonizados por estudiantes de Educación Secundaria.
El objetivo del concurso es fomentar el interés por la ciencia y la tecnología. Y ofrecer a los concursantes una oportunidad para ejercitar su creatividad y habilidades comunicativas usando herramientas que proporciona internet.
Ciencia Clip es una iniciativa de la Cátedra de Cultura Científica de la UPV/EHU y en la que colaboran Euskampus Fundazioa, Naukas, Scenio y Big Van.
Los ganadores de la edición 2022 ya están en la página web del concurso. La entrega premios y el anuncio del vídeo ganador del premio especial se realizarán durante el evento Naukas Bilbao. En la edición de 2020 resultó ganador en la categoría de 1º y 2º de de la ESO Javier Sirvent, de Alicante, con este vídeo:
Edición realizada por César Tomé López
El artículo CienciaClip 2020 – Lo que verías al viajar a la velocidad de la luz se ha escrito en Cuaderno de Cultura Científica.
Liberación controlada del fármaco con impresión 3D de almidones
Los métodos habituales producen medicamentos con determinados parámetros, pero en muchos casos sin satisfacer las necesidades individuales de los pacientes. De hecho, los medicamentos suelen basarse en la dosis para adultos, por lo que los pacientes pediátricos y de edad avanzada necesitan adaptarlos a las dosis adecuadas a su edad. Por otra parte, determinados pacientes o circunstancias necesitan alternativas de formas de dosificación específicas en la administración oral de los fármacos. En un extremo están los comprimidos de desintegración rápida, que se disuelven inmediatamente al colocarlos en la lengua. Pero, en el otro, está el reto de la liberación controlada del fármaco en el tiempo; sobre todo cuando el fármaco tiene un carácter hidrófobo, es decir, cuando resulta difícil que se disuelva en agua.
En esta línea, el Grupo ‘Materiales+Tecnologías’ (GMT) de la UPV/EHU desarrolla comprimidos basados en diferentes tipos de almidón mediante impresión 3D para terapias personalizadas. Han comprobado que la liberación del fármaco puede controlarse optimizando el tipo de almidón adecuado y la forma del comprimido.
 Fuente: UPV/EHU
Fuente: UPV/EHULa impresión 3D es una tecnología que consiste en la impresión de los productos capa por capa, en la que los materiales se depositan de acuerdo con el modelo digital dado por el software de diseño informático. Siguiendo una metodología rápida y sencilla y gracias a la impresión 3D, “hemos sido capaces de preparar comprimidos basados en tres tipos de almidón —dos tipos de almidón de maíz (normal y waxy) y un tipo de almidón de patata— con diferentes geometrías y cargadas con un fármaco no soluble”, indica Kizkitza González investigadora del GMT y primera autora del nuevo trabajo.
“El material que se produce hay que introducirlo en una jeringa antes de imprimirlo. Sin embargo, antes es fundamental asegurar que el material va a ser imprimible y que una vez imprimido va a mantener su forma. Para ello, hay que realizar un análisis reológico detallado”, explica la investigadora de la UPV/EHU. Los tres tipos de almidón han mostrado propiedades reológicas apropiadas, a pesar de que en el caso del almidón de patata el proceso de impresión resultó ser más laborioso debido a sus propiedades.
Asimismo, “hemos observado la importancia que tiene el origen botánico del almidón prácticamente en todas las propiedades como son la microestructura porosa, la formación de una red estable o la liberación del fármaco. En el caso del almidón de maíz normal la liberación del fármaco es instantánea y el medicamento se libera por completo en 10 minutos; en el caso del almidón de maíz waxy y el almidón de patata la liberación se da de una forma más continua, pudiendo tardar hasta 6 horas en liberarse por completo. Además, hemos podido demostrar la importancia que tiene la geometría del comprimido en la liberación del fármaco”, indica Kizkitza González.
Por último, “también se imprimieron comprimidos que combinaban diferentes tipos de almidón. En este caso, se consigue que la liberación tenga lugar en dos etapas. Por ejemplo, en el caso de una infección, en una primera etapa, con el almidón de maíz normal se podría liberar de inmediato un medicamento para paliar el dolor, y en una segunda etapa, con cualquiera de los otros dos tipos de almidón liberar un antibiótico de forma más continua”, cuenta la investigadora de la UPV/EHU.
Kizkitza González es consciente de que este trabajo es solo una primera etapa de un largo proceso, pero asegura que “los comprimidos impresos en 3D a base de almidón obtenidos mostraron propiedades prometedoras de cara a futuras aplicaciones de liberación de fármacos personalizadas”.
Referencia:
Kizkitza González, Izaskun Larraza, Garazi Berra, Arantxa Eceiza & Nagore Gabilondo (2022) 3D printing of customized all-starch tablets with combined release kinetics International Journal of Pharmaceutics doi: 10.1016/j.ijpharm.2022.121872
Para saber más:
Prótesis biocompatibles por impresión 3D
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Liberación controlada del fármaco con impresión 3D de almidones se ha escrito en Cuaderno de Cultura Científica.
Helmholtz, el físico que enseñó a los diapasones a hablar
Vivimos en el tiempo de las voces virtuales, un tiempo en el que uno casi tiene miedo de decir la palabra incorrecta, no vayan Siri, o Google, o Alexa, o Cortana a darse por aludidos. Podemos “oír” nuestro correo electrónico mientras cocinamos, escuchar libros que nunca nadie ha leído en voz alta, abrir las voces que nos esperan en nuestro buzón, o incluso preguntarle a un coche cuál es la mejor ruta a seguir. Las voces virtuales se han convertido en un lugar común, que ya casi no reparamos en ellas. Pero para poder sintetizarlas, grabarlas, transmitirlas o digitalizarlas, fue necesario entender primero cómo funciona nuestra propia voz y un físico capaz de enseñar a hablar a los diapasones.
Empecemos por lo básico: ¿dónde dirías que se forman las palabras cuando hablas? Sin pensarlo demasiado, ¿en el pecho, la boca, en la garganta quizás?
Hasta finales del siglo XVIII, esta pregunta no tenía una fácil respuesta. Muchos pensadores creían que el habla tiene su origen en las cuerdas vocales, quizás porque es lo primero que activamos y notamos vibrar al hablar. Otros argumentaban, en cambio, que la boca es lo que se mueve para pronunciar las distintas letras del lenguaje. Con el fin de aclarar esta disputa, en 1778 la Academia de Ciencias de Rusia lanzó un concurso dirigido a la comunidad científica. El premio recaería en aquella persona capaz de explicar la mecánica de las vocales humanas. Dos años más tarde, el profesor Christian Kratzenstein fue anunciado como ganador. No solo había logrado explicar por primera vez las diferencias acústicas entre los sonidos A E I O U, sino que además había fabricado una máquina capaz de producirlos artificialmente.
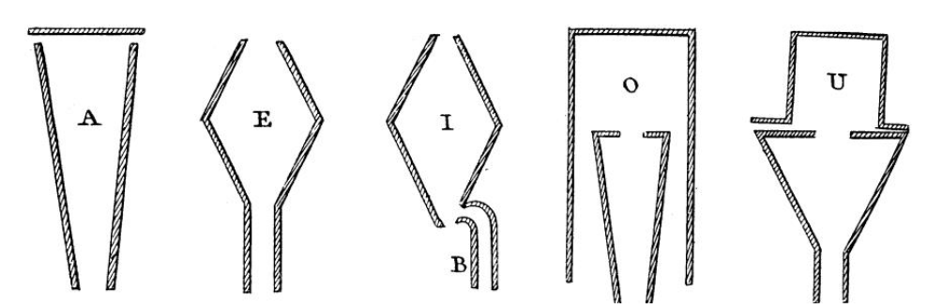 Las formas de los tubos de Kratzenstein para las cinco vocales. Fuente: F. Brackhane (2015) Kempelen vs. Kratzenstein –
Las formas de los tubos de Kratzenstein para las cinco vocales. Fuente: F. Brackhane (2015) Kempelen vs. Kratzenstein –Researchers on speech synthesis in times of change, ISCA-Speech.com
El invento consistía en una serie de tubos, parecidos a los de un órgano pero con formas mucho más variopintas. Estos tubos filtraban una nota producida por una lengüeta (parecida a la de una armónica) y daban lugar a los timbres de las vocales A E I O U. Era un mecanismo sorprendentemente sencillo. Pero así es como funciona nuestra propia voz. Puedes comprobarlo en primera persona: si yo ahora te pido que cantes una “u” y a continuación una “a”, ¿qué es lo que sucede exactamente en tu garganta, y en tu cara? Aunque sostengas todo el rato la misma nota con tu voz, la forma de tu tracto vocal (tu boca, en este caso) cambia para dar lugar a distintos timbres, igual que los tubos de la máquina de Kratzenstein.
Para entender cuál era la naturaleza de estos timbres de manera precisa, fue necesario esperar un siglo más. De hecho, la misma palabra “timbre” es difícil de definir y a menudo crea confusión. El timbre es lo que distingue a dos sonidos que tienen el mismo tono y la misma intensidad. Es decir, si yo cojo un violín, una trompeta, y una guitarra, y hago que toquen la misma nota (pongamos, un la 400 Hz), con la misma intensidad y la misma duración, la cualidad sonora que me permite distinguirlos es el timbre. La diferencia entre una “a” y una “u” es una diferencia tímbrica también. Ahora bien, desde un punto de vista físico, el timbre no es nada fácil de desentrañar.
En la segunda mitad del siglo XIX, Hermann von Helmholtz se empeñó en destilar esta propiedad del sonido. El físico alemán quería entender de qué estaban hechas las vocales del lenguaje1, y por extensión, el sonido de los instrumentos musicales. Lo que descubrió es que el timbre tiene mucho que ver con la complejidad de un sonido. Todo tono está compuesto por un montón de frecuencias. Esa composición (lo que en física conocemos como su espectro), y la manera en que cambia con el tiempo, es lo que determina en gran medida eso que percibimos como “timbre”.
Para demostrarlo, al igual que Kratzenstein, Helmholtz no se contentó con presentar simplemente su explicación. Con ayuda de Rudolph Koenig, construyó una máquina capaz de sintetizar esas mismas letras a partir de sus componentes fundamentales. Constaba de un conjunto de diapasones que se mantenían en constante vibración gracias a pulsos electromagnéticos. Cada diapasón producía una frecuencia pura de una serie armónica (frecuencias proporcionadas por números enteros 1, 2, 3, 4…). Al hacerlos vibrar con distintas intensidad relativa, era posible escuchar el sonido de las vocales. ¡Los diapasones, habían aprendido hablar!
 Sintetizador de Helmholtz. Fuente: Harvard Brain Tour
Sintetizador de Helmholtz. Fuente: Harvard Brain Tour
Aquel primitivo sintetizador ayudó a comprender mejor la naturaleza del habla y los sonidos de las vocales. Pero además, al otro lado del Atlántico, los diapasones de Helmholtz inspiraron a un joven Alexander Graham Bell, que empezó a soñar con convertir la voz humana en frecuencias eléctricas, capaces de recorrer enormes distancias a través un cable de cobre2. Un siglo después, las tataranietas de aquel extraño sueño, nos ofrecen ayuda desde nuestros dispositivos móviles. Sus voces digitales nos recuerdan que nuestras palabras, en último término, también están hechas de números.
Notas y referencias:
1Hermann von Helmholtz (1863) “On the Sensations of Tone”, traducido por Alexander J. Ellis. Via: Internet Archive.
2Cuento esta historia en más detalle en Almudena Martín Castro (2022). “La Lira Desafinada de Pitágoras”. HarperCollins.
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo Helmholtz, el físico que enseñó a los diapasones a hablar se ha escrito en Cuaderno de Cultura Científica.
El problema de los 17 caballos
 Foto: Louise Pilgaard / Unsplash
Foto: Louise Pilgaard / UnsplashEn ocasiones, cuando estoy pensando sobre qué escribir para la nueva entrada del Cuaderno de Cultura Científica, acudo a un libro que me gusta mucho, se trata del libro Famous Puzzles of Great Mathematicians (Rompecabezas famosos de grandes matemáticos), de Miodrag S. Petkovic. Hace poco revisaba algunos de los problemas de los que se habla en el libro cuando me topé con un clásico de la matemática recreativa, el problema de los 17 caballos, que también recibe otros nombres, como el problema de los 17 camellos, que es el nombre con el que yo lo conocía, o el problema de la herencia. El problema, en su forma más directa y sencilla, dice lo siguiente.
Problema de los 17 caballos: Un hombre muere y deja una herencia de diecisiete caballos que tiene que repartirse entre sus tres hijos en las proporciones 1/2 : 1/3 : 1/9 ¿Pueden los tres hermanos cumplir la voluntad de su padre?
Una rápida mirada a este problema nos dice que es un problema paradójico, o al menos problemático, puesto que 17 no se puede dividir ni por 2, ni por 3, ni por 9, luego la solución no va a ser inmediata si asumimos que los caballos no se pueden partir en trozos (por este motivo en algún texto matizan que los caballos tienen que repartirse vivos).
Este problema me recuerda a un problema chiste de una obra de teatro de los Hermanos Marx, de 1910, titulada Fun in High Skule:
Groucho: Si tuvieses 10 manzanas y quisieras repartirlas entre seis personas ¿qué harías tú?
Gummo: Haría compota de manzana.
Groucho: ¿Cuál es la forma de la Tierra?
Harpo: Pues no lo sé.
Groucho: Bien, veamos, ¿cuál es la forma de mis gemelos?
Harpo: Cuadrada.
Groucho: No los gemelos de diario, sino los que yo visto los domingos.
Harpo: Ah, redonda.
Groucho: Muy bien, ¿cuál es la forma de la Tierra?
Harpo: Cuadrada entre semana y redonda los domingos.
 Foto publicitaria, realizada por la Metro-Goldwyn-Mayer, de los Hermanos Marx en 1946
Foto publicitaria, realizada por la Metro-Goldwyn-Mayer, de los Hermanos Marx en 1946
Volviendo a la solución del problema de los 17 caballos, por una parte, tenemos la cuestión de que 17 no se puede dividir entre 2, 3 y 9, pero además si la herencia se repartiese completamente la suma de las proporciones 1/2, 1/3 y 1/9 debería ser 1, pero resulta que no es así:
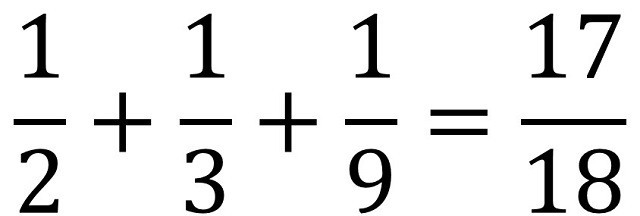
Es decir, la suma de las proporciones es menor que 1 y no se puede ejecutar toda la herencia. Por lo tanto, si nos vamos a una solución aritmética pura del problema, sin importarnos de qué estamos hablando, que es como muchas veces se resuelven los problemas matemáticos en la clase de esta signatura, tendríamos que la solución es 8,5 (17/2), 5,67 (en realidad, 17/3) y 1,89 (en realidad, 17/9) y se quedaría sin repartir el resto que es 0,94 (en realidad, 17 / 18), puesto que
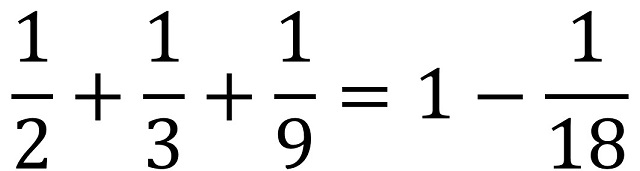
Si entendemos que la solución al problema de los 17 caballos tiene que ser siguiendo al pie de la letra las indicaciones de la herencia, que es como seguramente se entendía este problema matemático en sus orígenes, entonces tenemos dos opciones, o la solución puramente aritmética, como acabamos de describir, o pensar que es un problema imposible, en el sentido de que ni se puede dividir 17 entre 2, 3 y 9, ni la suma de esas partes, 17/2, 17/3 y 17/9 es toda la herencia, 17 caballos.
Según muchos textos, como el mencionado Famous Puzzles of Great Mathematicians, de Miodrag S. Petkovic o el texto The Penguin Dictionary of Curious and Interesting puzzles de David Wells, fue el matemático italiano Niccolo Fontana (1499 o 1500 – 1557), conocido como Tartaglia, quien sugirió la solución moderna de pedir prestado un caballo extra, así tener 18 caballos para repartir en tres partes de 9 (que es 18/2), 6 (que es 18/3) y 2 (que es 18/9) caballos, por lo que sobra 1, que se devuelve a la persona que lo había prestado.
Este problema, junto con su solución, se suele presentar como una legenda árabe, que dice lo siguiente (siguiendo la versión recogida por el matemático David Singmaster, en su libro Aventuras en las Matemáticas Recreativas, un interesante libro sobre la historia de la matemática recreativa).
Un jeque árabe murió dejando un rebaño de camellos como herencia completa para repartir entre sus tres hijos. En su testamento, especificó que el hijo mayor recibiría la mitad de la herencia; el segundo hijo, un tercio de la misma; y el tercero, una novena parte. Los hijos fueron a examinar el rebaño y descubrieron que había 17 camellos. Ahora bien, diecisiete no es divisible por dos, ni por tres, ni por nueve, y los hijos quedaron perplejos. Los camellos son valiosos y no querían cortar uno en pedazos.
Después de discutirlo, decidieron consultar al mullah Nasruddin y enviaron a buscarlo. El mullah se acercó con su camello y escuchó el dilema de los hijos del jeque. Después de reflexionar un poco, dijo que les prestaría un camello. El rebaño contaba ahora con 18 camellos y el mullah asignó la mitad de los camellos al hijo mayor, es decir, nueve camellos; luego un tercio de los camellos al segundo hijo, es decir, seis camellos; luego un noveno de los camellos al tercer hijo, es decir, dos camellos. Entonces, quedó un camello, el que les había prestado el mullah, así que este reclamó su camello y cabalgó hacia la puesta de sol.
 Imagen del problema de los 17 caballos, con el título Un legado inmanejable, perteneciente al libro Brandreth Puzzle Book (1896), que era a la vez un panfleto publicitario de las Pastillas de Brandreth y una colección de rompecabezas
Imagen del problema de los 17 caballos, con el título Un legado inmanejable, perteneciente al libro Brandreth Puzzle Book (1896), que era a la vez un panfleto publicitario de las Pastillas de Brandreth y una colección de rompecabezas
En general, podemos plantearnos el reparto de una cierta cantidad n de caballos en tres proporciones 1/a, 1/b y 1/c, donde a, b, c son números naturales distintos, tales que necesitemos el préstamo de un caballo para realizar el reparto, es decir, que se verifique la ecuación
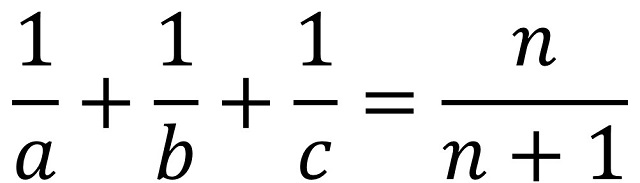
Por lo tanto, para construir todos los problemas de este tipo debemos de resolver la anterior ecuación diofántica (recordemos que las ecuaciones diofánticas son ecuaciones polinómicas de dos o más variables para las que se estudian las soluciones con números enteros, es decir, los naturales, el cero y los negativos). Existen siete soluciones (n; a, b, c) posibles, que mostramos a continuación:
(7; 2, 4, 8), (11; 2, 4, 6), (11; 2, 3, 12), (17; 2, 3, 9), (19; 2, 4, 5), (23; 2, 3, 8) y (41; 2, 3, 7),
con las cuales se pueden plantear problemas similares al problema de los 17 caballos, como así ha ocurrido con alguna de estas soluciones. Por ejemplo, Philip E. Bath en el problema El jardín del vicario de su libro Fun with Figures (Diversión con números) plantea el reparto de 7 chelines en las proporciones 1/2, 1/4 y 1/8; o S. E. Clark en el problema Los herederos y las ovejas de su libro Mental Nuts (Locuras mentales), que podéis encontrar en Internet Archive, plantea dividir una herencia de 19 ovejas en las proporciones 1/2, 1/4 y 1/5.
Si se permite que los números a, b y c no necesariamente son distintos, entonces se pueden obtener más soluciones, como (5; 2, 6, 6), (5; 3, 3, 6), (9; 2, 5, 5), (11; 3, 3, 4) o (3; 4, 4, 4).
 Portadas de los volúmenes 1 y 2 de Adventures in Recreational Mathematics, de David Singmaster
Portadas de los volúmenes 1 y 2 de Adventures in Recreational Mathematics, de David Singmaster
El matemático David Singmaster, en su libro Aventuras en las Matemáticas Recreativas, nos cuenta que este tipo de problemas son una versión moderna de algunos problemas antiguos de reparto donde las proporciones no sumaban uno. Problemas de este tipo son muy antiguos, ya aparecían en el Papiro de Rhind (escrito por el escriba Ahmes en el siglo XVI a.n.e.), que es el documento matemático más importante conservado del Antiguo Egipto.
 Fragmento del Papiro matemático de Rhind, o de Ahmes, perteneciente a la sección EA10057, British Museum
Fragmento del Papiro matemático de Rhind, o de Ahmes, perteneciente a la sección EA10057, British Museum
Terminemos esta entrada con el problema 63 del Papiro de Rhind que consiste en repartir 700 barras de pan para cuatro personas, en las proporciones 2/3 : 1/2 : 1/3 : 1/4, pero el total de las partes suma 7/4, que es mayor que 1.
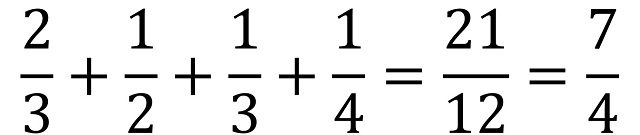
La solución al problema que se ofrece en el texto matemático egipcio es que, si 700 barras se corresponden con 7/4, entonces, la unidad es 4/7 de 700, es decir, 400 y se realiza el reparto de 2/3, 1/2, 1/3 y 1/4 de la unidad, es decir, que la cantidad de panes se reparte en 266,7 (2/3 de 400) barras de pan –o podríamos decir que 266 barras enteras y dos terceras partes de una barra-, 200 (1/2 de 400) barras, 133,3 (1/3 de 400) barras –podríamos decir que 133 barras de pan y una tercera parte de una- y 100 (1/4 de 400) barras.
Bibliografía:
1.- Miodrag S. Petrovic, Famous Puzzles of Great Mathematicians, AMS, 2009.
2.- David Wells, The Penguin Dictionary of Curious and Interesting puzzles, Penguin, 1992.
3.- Martin Gardner, Fractal Music, Hypercards and more, W. H. Freeman & Co, 1991.
4.- David Singmaster, Adventures in Recreational Mathematics (Problem Solving in Mathematics and Beyond, 21), vol. 1 y 2, World Scientific, 2021.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo El problema de los 17 caballos se ha escrito en Cuaderno de Cultura Científica.
Einstein y Johannes Stark
Johannes Stark fue un físico alemán, ganador del premio Nobel en 1919 por el descubrimiento de que en un campo eléctrico la luz se separa en líneas espectrales, fenómeno conocido en su honor como efecto Stark. Conforme comenzaba su ascenso a la fama Einstein se carteó con regularidad con Stark. En 1913 Stark modificó la ley de fotoequivalencia de Einstein, que actualmente se llama ley de Stark-Einstein o segunda ley de la fotoquímica. Tras la Primera Guerra Mundial, sin embargo, Stark abrazó fervientemente los ideales nazis, promoviendo una ciencia nueva completamente “aria” y orquestando toda una campaña de descrédito de la “judía” teoría de la relatividad de Einstein.
 Johannes Stark. Foto: nobelprize.com
Johannes Stark. Foto: nobelprize.comEn 1907, Stark, que era entonces profesor en la Technische Hochschule de Hannover, pidió a Einstein que escribiese un artículo de revisión sobre la relatividad para el Jahrbook für Radioaktivität und Elekronik (Anuario de radioactividad y electrónica). Durante esta época y en los años siguientes, Einstein y Stark mantuvieron una correspondencia bastante cordial. Solamente una excepción. Ocurrió cuando Einstein estaba viviendo en Praga y escribió un artículo sobre procesos fotoquímicos que Stark creyó que plagiaba directamente uno de sus escritos. Stark atacó a Einstein en las páginas de Annalen der Physik, a lo que Einstein respondió contundentemente en la misma revista demostrando que Stark no había entendido su trabajo.
1913 fue el annus mirabilis particular de Johannes Stark. Ese año Stark modificó una teoría sobre los fotones publicada por Einstein en 1906. La versión definitiva, conocida actualmente como ley de Stark-Einstein, o segunda ley de la fotoquímica, afirma que cada molécula implicada en una reacción fotoquímica absorbe solamente un único fotón de la radiación o luz que causa la reacción. Ese año, Stark también descubrió un efecto de la luz que ha llevado su nombre desde entonces.
Los científicos ya conocían lo que se llamaba el efecto Zeeman, en el que los campos magnéticos dividen la radiación procedente de partículas en las denominadas líneas espectrales. Estas líneas dependen de la velocidad a la que un átomo o ión dado está oscilando y pueden ser útiles a la hora de identificar exactamente qué partícula es la que está oscilando. Stark se las arregló para producir líneas espectrales similares usando un campo eléctrico en vez de uno magnético. En última instancia, el efecto Stark es más complejo a la hora de analizar la información obtenida, por lo que hoy día se prefiere usar el efecto Zeeman para el análisis de la estructura atómica.
En cualquier caso este era un trabajo que merecía un Nobel; Stark recibió el premio en 1919. En su discurso de aceptación ya aparecieron los primeros indicios de lo que más tarde serían sus posiciones políticas. El discurso comienza con la idea de que los alemanes continúan con el trabajo de los antiguos griegos de comprender la estructura atómica. A lo largo del discurso su argumentación, una y otra vez, es siempre cómo su trabajo se enmarca y contribuye a la física alemana. Las semillas del nacionalismo están enraizadas y comienzan a verse sus primeros brotes.
Tras el premio Nobel, Stark, si se me permite la expresión, pasa definitivamente al lado oscuro. No se le recuerda por sus contribuciones a la ciencia en la segunda mitad de su vida, sino por su política. Qué acontecimientos o influencias pudieron hacer que Stark se volviese contra los que hasta entonces habían sido sus colegas no están claros, pero lo cierto es que en los años veinte Stark absorbió y aceptó plenamente la retórica nazi de la gloria de la raza aria y comenzó una campaña para socavar la física moderna, lo que incluía un rencoroso ataque contra Einstein.
En 1922, cuando era profesor en la Universidad de Wurzberg, Stark escribió un libro denunciando la física moderna llamado La crisis actual en la física alemana. Afirmaba en él que materias como la relatividad eran obviamente subversiones, subversiones judías además, del pensamiento racional puro. Si bien el nazismo y su antisemitismo estaban creciendo en Alemania, todavía no eran mayoritarios y este tipo de comentarios le valió el ostracismo por parte de sus colegas. Sus afirmaciones le llevaron a tener que renunciar a su cátedra y tuvo que ganarse la vida creando una empresa de porcelana.
En 1924, Stark declaró públicamente su completa lealtad a Hitler y continuó atacando a la física “judía”, afirmando que era una ciencia que ignoraba los experimentos objetivos o la observación de los hechos. En los años 30 trabajó con Philipp Lénárd, otro premio Nobel con tendencias nacionalistas extremas que también la había tomado con Einstein, intentando crear una ciencia alemana “pura”, de forma similar a como Hitler estaba tratando de crear una raza alemana “pura”.
Stark fue nombrado presidente del Instituto Imperial de Física y Tecnología tras la llegada al poder de Hitler en 1933, cargo que ocuparía hasta 1939. En esta posición disponía de una plataforma inmejorable para la difusión de su retórica de que toda la ciencia debía dedicarse a apoyar las filosofías nazis. Afirmó que los judíos, por su evidente falta de respeto a la verdad, no eran adecuados para la física.
O lo que era peor desde su punto de vista, no se limitaban a los canales apropiados. Escribió, aparentemente con Einstein en mente, en su libro Nacionalsocialismo y Ciencia, publicado en 1934: “el celo dogmático e impulso propagandístico del científico judío le lleva a informar de sus descubrimientos no sólo en publicaciones científicas sino también en la prensa diaria o en conferencias públicas”.
En general, los ataques de Stark a la ciencia moderna no tenían una base racional: se limitaba a declarar que la relatividad era tan contraria a la experiencia diaria y al sentido común que tenía que ser errónea. Cuando Werner Heisenberg salió en defensa de Einstein, Stark lo tildó, en un artículo en el periódico oficial de la SS, Das Schwarze Korps, de “judío blanco” que debería “desaparecer” (Heisenberg se salvó usando sus contactos familiares con el Reichführer-SS Heinrich Himmler, pero esta es otra historia).
Tras la Segunda Guerra Mundial, el tribunal de desnazificación de Baviera juzgó a Stark. Einstein, viendo el panorama que se cernía sobre Alemania y el peligro real que corría su vida, la había abandonado en 1933 para no volver. Pero aún quedaban científicos para atestiguar en contra de Stark: Max von Laue, Werner Heisenberg y Arnold Sommerfeld entre ellos. Stark fue considerado “major offender” (nivel 5, el más alto de los cinco posibles niveles de colaboración con el régimen nazi, según la clasificación seguida en los tribunales constituidos en la Alemania ocupada por los Estados Unidos). Fue condenado a 4 años de trabajos forzados. La sentencia fue suspendida y Stark se retiró al campo, donde trabajó solo y aislado en su laboratorio privado hasta su muerte en 1957.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Una versión anterior de este artículo se publicó en Experientia Docet el 6 de septiembre de 2009.
El artículo Einstein y Johannes Stark se ha escrito en Cuaderno de Cultura Científica.
De casquetes polares y hielo de dióxido de carbono
Una de las cosas que quizás más sorprenden de Marte, cuando lo vemos a través de un potente telescopio o en las imágenes que nos llegan de las misiones espaciales, es la presencia de sus casquetes polares, que destacan por su color blanco, a veces inmaculado, en contraste con el color rojo de su superficie.
Nos es más llamativo todavía porque los vemos crecer y menguar con las estaciones, al igual que en nuestro planeta, aunque con un ciclo prácticamente restringido a la sublimación y a la formación de los hielos por condensación desde la atmósfera debido a las bajas temperaturas y ligera presión atmosférica.
Desde el punto de vista de la geología, el hielo es un importante agente de modelado y transporte, ya que los hielos son capaces de viajar cientos e incluso miles de kilómetros, erosionando la superficie y encajándose, formando grandes valles.
Además, las acumulaciones de hielo pueden ser estudiadas como los estratos de la roca, lo que nos aporta una valiosa información sobre el clima de un planeta a lo largo del tiempo, estudiando las burbujas de aire atrapadas y las capas de polvo, que, si me permiten la metáfora, se alternan como una inmensa tarta de chocolate y galleta.
 Un escarpe en el casquete del polo norte de Marte. Se pueden apreciar algunas de sus capas, especialmente donde se encuentran intercaladas por otras de polvo. Imagen cortesía de NASA/JPL-Caltech/UArizona.
Un escarpe en el casquete del polo norte de Marte. Se pueden apreciar algunas de sus capas, especialmente donde se encuentran intercaladas por otras de polvo. Imagen cortesía de NASA/JPL-Caltech/UArizona.Pero, además, se da la casualidad de que precisamente el hielo, junto con el viento, es uno de los agentes de modelado del relieve más activos en el planeta Marte en la actualidad, por lo que conocer la dinámica glacial del planeta es un asunto de gran interés para geólogos y climatólogos. Aunque eso sí, hoy nos centraremos solo en los casquetes de hielo, en otra ocasión hablaremos sobre los cinturones glaciales que hay en latitudes más bajas.
Hace varias décadas los científicos pensaban que estos casquetes polares estaban formados principalmente por hielo de dióxido de carbono, mientras que ahora sabemos que, probablemente, al menos en el polo sur, esa cifra esté más cerca del 1%, y que el resto sea hielo de agua, de tal manera que si se fundiese todo este hielo una importante parte de la superficie de Marte quedaría sumergida bajo las aguas.
 Casquete polar sur del planeta Marte. Se aprecia perfectamente el color blanco del hielo, así como zonas más rojizas cubiertas por el polvo. Cortesía de ESA/DLR/FU Berlin / Bill Dunford.
Casquete polar sur del planeta Marte. Se aprecia perfectamente el color blanco del hielo, así como zonas más rojizas cubiertas por el polvo. Cortesía de ESA/DLR/FU Berlin / Bill Dunford.A pesar de ese porcentaje tan bajo de dióxido de carbono, el volumen total de hielo de dióxido de carbono que alberga el casquete del polo sur es de unos 16000 kilómetros cúbicos, suficiente como para llenar el lago Superior, el lago más grande de los Grandes Lagos de Norteamérica -valga la redundancia-, de este hielo, y que en algunos lugares llega a formar capas de más de un kilómetro de potencia o espesor, mientras que el casquete en su conjunto tiene un espesor total de unos cuatro kilómetros.
Y bueno, ¿cómo conocemos estos datos? En las últimas dos décadas hemos podido hacer perfiles de la estructura de los polos marcianos gracias a dos instrumentos conocidos como MARSIS, que viaja en la sonda europea Mars Express, y SHARAD que equipa a la misión Mars Reconnaissance Orbiter, que no son más que dos radares que nos permiten «ver» con sus ondas hasta cierta profundidad, ayudándonos a estudiar las capas más someras del subsuelo marciano y cuáles son las relaciones entre estas.
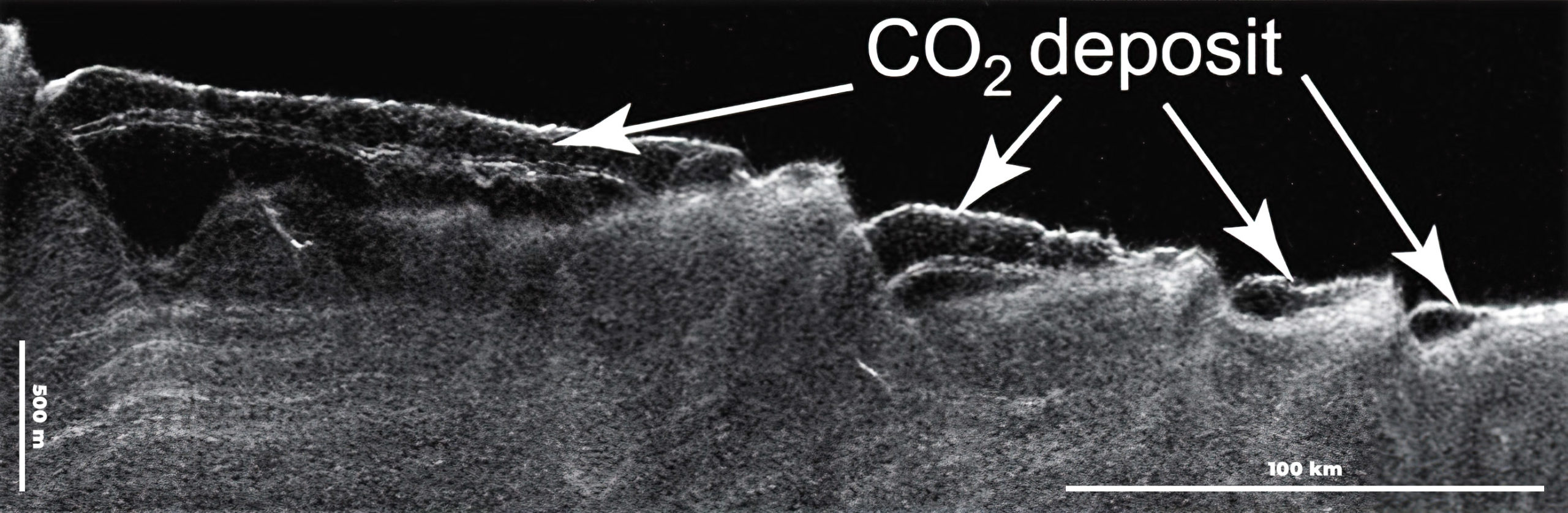 Perfil de radar tomado por el instrumento SHARAD, que se encuentra a bordo de la Mars Reconnaissance Orbiter. Se aprecian perfectamente las acumulaciones de hielos de dióxido de carbono ocupando depresiones que favorecen su depósito. Imagen cortesía de NASA/JPL-Caltech/Sapienza University of Rome/Southwest Research Institute.
Perfil de radar tomado por el instrumento SHARAD, que se encuentra a bordo de la Mars Reconnaissance Orbiter. Se aprecian perfectamente las acumulaciones de hielos de dióxido de carbono ocupando depresiones que favorecen su depósito. Imagen cortesía de NASA/JPL-Caltech/Sapienza University of Rome/Southwest Research Institute.Pero el poder ver la estructura interna de las capas de hielo nos solo no resolvió nuestras dudas, sino que nos hizo enfrentarnos a nuevas preguntas… y es que la condensación de dióxido de carbono atmosférico que da lugar a los hielos que se acumulan en los polos va depositando capas muy finas, algo parecido a nuestras escarchas invernales, relacionada además con los ciclos climáticos de Marte, que dependen en gran medida de la inclinación de su eje con respecto al Sol: cuanto menos esté inclinado, menor insolación llegará a los polos y, por lo tanto, el clima será lo suficientemente frío como para favorecer las acumulaciones de dióxido de carbono.
Aun así, en primavera y verano el aumento de las temperaturas podría provocar la sublimación de las capas de hielo más superficiales, haciendo que la acumulación de este hielo de dióxido de carbono fuese muy lenta incluso en largos periodos de tiempo. Entonces, ¿qué provoca esos grandes espesores que vemos en las capas de hielo de dióxido de carbono y la forma de las acumulaciones? Un estudio publicado el pasado mes de abril intenta resolver estas cuestiones aplicando nuestro conocimiento de los glaciares en la Tierra, adaptando los modelos que usamos hoy día para estudiar el movimiento glacial y adaptándolo a las observaciones realizadas en Marte y a sus condiciones de gravedad, tipos de hielo y clima.
Los resultados indican que los depósitos de hielo de dióxido de carbono se habrían formado por la existencia de glaciares de este compuesto, capaces de moverse por la superficie a una velocidad de unas cien veces superior a la que lo hace el hielo de agua en el planeta Marte.
 Erosión provocada por la sublimación del hielo de dióxido de carbono en el casquete polar del hemisferio sur de Marte. Imagen cortesía de NASA/JPL-Caltech/UArizona.
Erosión provocada por la sublimación del hielo de dióxido de carbono en el casquete polar del hemisferio sur de Marte. Imagen cortesía de NASA/JPL-Caltech/UArizona.Esto permite al hielo de dióxido de carbono avanzar y e ir cayendo sobre depresiones donde lentamente va acumulándose y formando estos espesores que observamos, como una enorme pero lenta cascada de hielo, al mismo tiempo evitando que en primavera y verano se sublime la mayor parte.
De hecho, muchas de las morfologías glaciares que vemos en el casquete de hielo del polo sur en realidad están formadas por los hielos de dióxido de carbono, mientras que los hielos de agua prácticamente podríamos decir que se encuentran en una situación estática en comparación con la dinámica de estos hielos.
Es cierto que este tipo de hielo nos puede parecer exótico, pero no podemos olvidar que, además del hielo de agua, en el Sistema Solar hay un tercer tipo, el de nitrógeno, que se descubrió en Plutón. Y es importante que sigamos estudiando los hielos, por su papel en el modelado del paisaje, pero también porque nos cuentan una apasionante historia de ciclos climáticos de otros planetas que quizás en algún futuro seremos capaces de descifrar.
Referencias:
Smith, I. B., Schlegel, N.-J., Larour, E., Isola, I., Buhler, P. B., Putzig, N. E., & Greve, R. (2022). Carbon dioxide ice glaciers at the south pole of Mars. Journal of Geophysical Research: Planets, 127, e2022JE007193. 10.1029/2022JE007193
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo De casquetes polares y hielo de dióxido de carbono se ha escrito en Cuaderno de Cultura Científica.
Somos simios caros
 Foto: Sasha Freemind / Unsplash
Foto: Sasha Freemind / UnsplashEs cosa sabida que los seres humanos tenemos un encéfalo comparativamente más grande que el del resto de los mamíferos, y también que el de los grandes simios -bonobos, chimpancés, gorilas y orangutanes- que son nuestros parientes evolutivos más próximos. En parte por esa razón y en parte por su elevado nivel de actividad metabólica, nuestro encéfalo resulta ser un órgano caro. Consume del orden del 20% de la energía que gastamos en condiciones de mínima actividad física.
No solo gastamos más en tejido nervioso. En poblaciones en las que no se ejerce control artificial alguno sobre la reproducción, los seres humanos tienen más crías y las tienen de mayor tamaño que las de cualquiera de los demás homínidos. También vivimos más años, bastantes más de los que cabría esperar de un mamífero de unos 60 kg de masa; para vivir más hace falta dedicar más recursos energéticos al mantenimiento y reparación de los tejidos.
Nuestro sistema digestivo, gracias al consumo de alimentos de digestión más fácil -carne y productos cocinados, principalmente- se ha reducido mucho con relación al de nuestros ancestros, y gasta por ello mucha menos energía. Además, nos desplazamos de forma más eficiente que esos otros homínidos. Pero esos factores no tienen un efecto de la entidad suficiente como para compensar las consecuencias de poseer un encéfalo cuyo gasto se ha elevado tanto, así como de los costes asociados a una mayor intensidad reproductiva y una longevidad más prolongada.
El metabolismo es el conjunto de procesos químicos que sustentan las actividades que desarrolla un ser vivo. Por tanto, el gasto metabólico total es el que resulta de agregar el correspondiente a cada una de esas actividades. Están, por un lado, aquellas cuya finalidad es el mantenimiento de los sistemas vitales; a estas corresponde un nivel de actividad metabólica que denominamos basal. Viene a ser el mínimo nivel metabólico necesario para mantenernos con vida. Tenemos, por otro lado, las implicadas en la defensa frente a patógenos, las que lleva a cabo el sistema inmunitario; cuantas más enfermedades infecciosas se sufren, más energía hay que gastar para combatirlas. Otras sirven para hacer reparaciones. Están también el crecimiento y la reproducción, actividades que comportan la producción de nuevos tejidos y que son, por ello, bastante costosas, muy especialmente para las madres. Y tenemos, por último, las que implican una cierta acción sobre el entorno, como son el desplazamiento o el trabajo.
Cuando se compara el gasto metabólico diario total de las diferentes especies de homínidos, se observa que la nuestra es la que, para un ejemplar de la misma masa (sustraída la grasa corporal), experimenta un mayor gasto de energía. Y ello se debe a que el metabolismo basal de órganos y tejidos es, en general, más elevado (encéfalo, sistema digestivo e hígado son órganos con un gasto comparativamente alto) que el de otros homínidos. Y también, aunque en una medida menor, a que somos más activos que los miembros de esas especies.
Los individuos de nuestra especie gastamos más energía que nuestros parientes evolutivos más próximos para mantenernos con vida, crecer y reproducirnos. También somos más activos, en parte para conseguir la energía que necesitamos para afrontar ese mayor gasto. Y esto explica un dato poco conocido: los seres humanos almacenan, especialmente las mujeres, mucha más grasa que los demás simios. Es lógico que así sea; al gastar tanto, conviene dotarse de reservas abundantes porque, antes o después, vendrán mal dadas y cuando eso ocurra serán necesarias para sobrevivir. Y esto explica en parte que, una vez almacenada esa grasa, sea tan difícil deshacerse de ella.
Fuente: Pontzer, H., Brown, M., Raichlen, D. et al. Metabolic acceleration and the evolution of human brain size and life history. Nature 533, 390–392 (2016).
Para saber más:
La estufa interior
Las actividades animales
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Somos simios caros se ha escrito en Cuaderno de Cultura Científica.
CienciaClip 2021 – Cristalizaciones: cómo hacer el mejor cristal

Ciencia Clip es un concurso de vídeos divulgativos de ciencia diseñados, producidos y protagonizados por estudiantes de Educación Secundaria.
El objetivo del concurso es fomentar el interés por la ciencia y la tecnología. Y ofrecer a los concursantes una oportunidad para ejercitar su creatividad y habilidades comunicativas usando herramientas que proporciona internet.
Ciencia Clip es una iniciativa de la Cátedra de Cultura Científica de la UPV/EHU y en la que colaboran Euskampus Fundazioa, Naukas, Scenio y Big Van.
Los ganadores de la edición 2022 ya están en la página web del concurso. La entrega premios y el anuncio del vídeo ganador del premio especial se realizarán durante el evento Naukas Bilbao. En la edición de 2021 resultó ganador en la categoría de 1º y 2º de Bachillerato Marina Faura, de Madrid, con este vídeo:
Edición realizada por César Tomé López
El artículo CienciaClip 2021 – Cristalizaciones: cómo hacer el mejor cristal se ha escrito en Cuaderno de Cultura Científica.
Lo que los sedimentos de hace 56 millones de años nos dicen del cambio climático
El Departamento de Geología de la UPV/EHU ha investigado sedimentos de hace 56 millones de años en la cuenca de Tremp-Graus (en el límite entre Lérida y Huesca). Del estudio se deduce que el calentamiento global de entonces tuvo tres fases en las que la distribución de las precipitaciones fue diferente. Los datos del estudio pueden servir para ajustar los modelos matemáticos utilizados para predecir los efectos del cambio climático actual.

Hace 56 millones de años se produjeron grandes emisiones de carbono a la atmósfera y a los océanos, lo que provocó un fuerte calentamiento global, denominado Máximo Térmico del Paleoceno-Eoceno, y es considerado un análogo antiguo del actual calentamiento antropogénico. “A pesar de que el origen o la causa del calentamiento de aquella época era diferente, el proceso fue muy similar al calentamiento global actual. Se sabe que el clima se calentó, pero con un cambio climático pueden darse otras alteraciones aparte del calentamiento. En concreto, hemos querido analizar cómo cambiaron entonces las condiciones hidroclimáticas en cuanto a precipitaciones”, ha señalado Aitor Payros, primer autor del estudio.
El Departamento de Geología de la UPV/EHU ha investigado los cambios aluviales e hidroclimáticos en latitudes medias registrados en la cuenca de Tremp-Graus (en el límite entre Lérida y Huesca) durante el Máximo Térmico del Paleoceno-Eoceno, y ha llegado a la conclusión de que lo que entonces ocurrió podría ser algo similar a lo que ya está sucediendo en la actualidad en el sudeste de la península ibérica. Para ello, han recopilado datos históricos de la región, y han encontrado similitudes tanto geográficas como hidroclimáticas.
Según Aitor Payros, “hemos visto que el calentamiento global modificó la distribución estacional de las precipitaciones y que además se modificó en varias fases. Al principio, las precipitaciones se concentraron en unos pocos meses, en torno al otoño; posteriormente, se distribuyeron de forma más homogénea a lo largo del año. Y, sin embargo, la última fase tendió a una mayor sequía”. En opinión de Payros, “no podemos decir que el calentamiento global provoca un aumento de las temperaturas o que las precipitaciones son más fuertes, simplemente. Las cosas no son tan simples. Se producen cambios, pero estos no se mantienen durante todo el periodo de calentamiento global. Dentro del calentamiento global pueden existir varias fases”.
Mirar al pasado para predecir el futuro“Hemos observado que al inicio de aquel calentamiento global se produjo un aumento de los contrastes estacionales en cuanto a las precipitaciones. Es decir, las precipitaciones se concentraban en torno al otoño (con frecuentes tormentas e inundaciones de gran magnitud) y en el resto de los meses se registraban periodos de sequía. Y eso es precisamente lo que está sucediendo en las últimas décadas, y en el último siglo, en el sudeste de la península ibérica: las lluvias intensas son cada vez más frecuentes en torno al otoño y al final del verano, y eso no ocurría hace 100 o 200 años”, explica Payros.
El investigador señala que no se puede saber qué es lo que ocurrirá en el futuro en el sudeste de la península ibérica, “pero si suponemos que la Tierra responde de forma similar a los mismos fenómenos o similares, podríamos pensar que en el futuro la distribución anual de las precipitaciones podría ser más homogénea en el sudeste peninsular o en otras regiones de clima similar”.
Payros reivindica el valor que puede tener el estudio de los paleoclimas: “Nosotros vemos lo que ocurrió hace millones de años. Y si aquello que ocurrió se repite una y otra vez, es decir, si la Tierra responde siempre de la misma manera a ciertos fenómenos, podemos pensar que en el futuro también seguirá funcionando de la misma manera”. Este tipo de investigaciones pueden servir para hacer previsiones de futuro: “Cuando los modelos informáticos o matemáticos utilizados para predecir el clima sean capaces de reproducir los fenómenos que tuvieron lugar durante los antiguos calentamientos globales, entonces serán capaces de prever los cambios que se producirán en el futuro. Dichos modelos informáticos y matemáticos pueden ajustarse con nuestros datos”.
Referencia:
Aitor Payros, Victoriano Pujalte, Birger Schmitz (2022) Mid-latitude alluvial and hydroclimatic changes during the Paleocene– Eocene Thermal Maximum as recorded in the Tremp-Graus Basin, Spain Sedimentary Geology doi: 10.1016/j.sedgeo.2022.106155
Para saber más:
Los misterios que rodean al máximo térmico de hace 56 millones de años
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Lo que los sedimentos de hace 56 millones de años nos dicen del cambio climático se ha escrito en Cuaderno de Cultura Científica.
El rugido de las rocas costeras
En Geología también tenemos nuestros bufones particulares. Y no me estoy refiriendo a que haya profesionales de las Ciencias de la Tierra que se dediquen con ahínco a hacer bromas para echarnos unas risas de vez en cuando, aunque generalmente tenemos buen humor y acabamos buscando la cara divertida y sarcástica de los fósiles, rocas o estructuras con las que estemos trabajando. Me estoy refiriendo a otra acepción de la palabra bufón, a una muy geológica.
 Bufón de Santiuste, Monumento Natural del litoral de la localidad de Llanes, Asturias.Fuente: turismoasturias.es (CC-by 3.0)
Bufón de Santiuste, Monumento Natural del litoral de la localidad de Llanes, Asturias.Fuente: turismoasturias.es (CC-by 3.0)Si durante este verano habéis pasado unos días de relax en alguna zona litoral, principalmente en el norte de la Península Ibérica, y os habéis lanzado a dar un buen paseo por encima de los acantilados rocosos de estas costas, es posible que os hayáis llevado algún pequeño susto cuando un chorro de aire y agua marina brotando con furia del suelo os haya cortado el camino. Pues eso es un bufón.
Como definición rápida, un bufón es una estructura geológica que se genera en acantilados costeros formados por rocas que son susceptibles de sufrir disolución por la acción del agua, tales como las rocas carbonatadas. Pero no es un proceso sencillo, ya que es necesario que la disolución producida por el agua actúe a dos niveles diferentes: tanto en la parte superficial del terreno como en el interior de las propias rocas del acantilado.
En superficie, el agua de lluvia disuelve las rocas carbonatadas formando unos conductos que se adentran hacia el interior del terreno de forma más o menos vertical, dando lugar a unas estructuras que reciben diversas denominaciones de acuerdo a su tamaño y morfología, como son las simas o las dolinas. Ya en el interior, esta agua subterránea va a circular en dirección al mar, provocando la disolución de las rocas con una orientación próxima a la horizontal, dando lugar así a unas estructuras que conocemos como galerías.
Pero el agua del mar no se va a quedar como una simple espectadora silenciosa en todo este proceso, también va a tomar parte de la magia geológica. Y esto es debido a que la acción continua del oleaje provoca la erosión del acantilado rocoso y el retroceso del litoral, pudiendo llegar a conectar alguna de esas galerías subterráneas directamente con el mar.
Ahora es cuando todas las piezas del puzle encajan, ya que tenemos una sima vertical que está conectada con una galería subterránea que, a su vez, está conectada directamente con el mar. La geología ya ha hecho su trabajo, a partir de aquí entra en juego la física de fluidos.
 Estructura de un bufón litoral. Fuente: Wikimedia Commons
Estructura de un bufón litoral. Fuente: Wikimedia CommonsCuando se dan ciertas condiciones de oleaje, muchas veces favorecidas por la marea alta, el agua del mar puede penetrar en el interior de los acantilados a través de las galerías subterráneas. Ahí es canalizada y circula a presión por las simas verticales, llegando a salir a superficie como un chorro de espuma, aire y agua vaporizada.
Esta salida a la superficie del agua a presión genera, a su vez, un efecto sonoro muy particular, ya que parece que se produjese un tremendo resoplido o bramido. Es decir, un bufido. Y es precisamente de esta palabra de donde procede el nombre de este proceso geológico.
 Campo de bufones de Arenillas, Monumento Natural del litoral de la localidad de Llanes, Asturias. Fuente: turismoasturias.es (CC-by 3.0)
Campo de bufones de Arenillas, Monumento Natural del litoral de la localidad de Llanes, Asturias. Fuente: turismoasturias.es (CC-by 3.0)Aunque podemos encontrarnos con bufones aislados en ciertas áreas costeras, lo más habitual es que se produzcan varias estructuras más o menos agrupadas en una misma zona, dando lugar a lo que conocemos como campos de bufones. Además, los podemos encontrar de todos los tamaños que podamos imaginarnos, ya que, dependiendo de la longitud vertical y el diámetro de la sima o conducto por el que asciende el agua marina y de la presión de la misma, el chorro expulsado puede alcanzar varios metros de altura.
Esto convierte a los bufones en unas maravillas naturales con una belleza hipnótica, llegando a ser un auténtico espectáculo en momentos de temporal y mar muy picada, pero también se pueden transformar en unas estructuras peligrosas. No es recomendable acercarse mucho al litoral cuando el mar está embravecido, porque la fuerza del oleaje puede provocar que el agua expulsada por los bufones tenga la fuerza suficiente para hacer mucho daño a una persona adulta. Es mejor disfrutar del espectáculo a cierta distancia, por si acaso.
En el vídeo, Peine del Viento, en San Sebastián / Donostia. En primer término se ven y oyen 7 bufones artificiales en acción.
Para saber más:
La geodiversidad que nos rodea
El Peine del Viento de Chillida: materia, forma y lugar
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo El rugido de las rocas costeras se ha escrito en Cuaderno de Cultura Científica.
Maryna Viazovska, la matemática que empaqueta esferas
Profesora en la Cátedra de Teoría de Números en el Instituto de Matemáticas de la Escuela Politécnica Federal de Lausana (EPFL), Maryna Viazovska fue galardonada con la Medalla Fields en julio de 2022. Se premiaba su trabajo sobre el empaquetamiento de esferas: resolvió en 2016 el problema del empaquetamiento en dimensión 8 y, en colaboración con otros investigadores, en dimensión 24.
Los tiranos no pueden impedir que hagamos matemáticas. Al menos hay algo que no nos pueden quitar.
 Maryna Viazovska. Fuente: EPFL/Fred Merz.
Maryna Viazovska. Fuente: EPFL/Fred Merz.
Nacida en Kiev el 2 de diciembre de 1984, Maryna Viazovska es la mayor de tres hermanas en una familia muy cercana a la ciencia: su madre es ingeniera y su padre, químico. Casada con el físico ucraniano Daniil Evtushinsky, el matrimonio tiene un hijo y una hija.
Maryna eligió las matemáticas desde pequeña, se le daban especialmente bien en la escuela. En una de las entrevistas concedidas tras recibir la Medalla Fields, comentaba que era rápida para las matemáticas, pero no tanto para la lengua, aunque le gustaba leer, especialmente libros de ciencia ficción.
En 1998 ingresó en el Liceo de Ciencias Naturales de Kiev no. 145, una institución de enseñanza secundaria especializada en matemáticas, física y computación. Su alumnado se selecciona entre personas destacadas, como Maryna, cuyo rendimiento en matemáticas era superior a la media. Tras graduarse en 2001, ingresó en la Universidad Nacional Taras Shevchenko de Kiev para estudiar matemáticas; allí obtuvo su licenciatura en 2005. Después viajó a Alemania para cursar una maestría en la Universidad Técnica de Kaiserslautern, graduándose en 2007. En mayo de 2010 defendió su tesis de Candidato de Ciencias en el Instituto de Matemáticas de la Academia Nacional de Ciencias de Ucrania.
Después de obtener este título viajó, al Instituto Max Planck de Matemáticas en la Universidad de Bonn, donde realizó la tesis doctoral bajo la supervisión del especialista en teoría de números Don Zagier (1951). Defendida en 2013, esta memoria trataba sobre funciones modulares.
Después de un tiempo como investigadora postdoctoral en el Institut des Hautes Études Scientifiques en Francia, en 2014 Viazovska se mudó a Berlín donde trabajó en la Escuela Matemática de Berlín y la Universidad Humboldt de Berlín.
En enero de 2018 consiguió la cátedra que actualmente ocupa en la EPFL.
El problema de empaquetamiento de esferasLa conjetura de Kepler fue enunciada por Johannes Kepler (1571-1630) en su ensayo Strena seu de nive sexangula de 1611. El astrónomo comenzó a interesarse por los ordenamientos de esferas gracias a su correspondencia con el matemático y astrónomo Thomas Harriot (1560-1621). El marino Walter Raleigh (1552-1618) había planteado a Harriot el problema de encontrar la mejor manera de amontonar balas de cañón en la cubierta de sus barcos. Y Harriot se lo comentó a Kepler, quien conjeturó que la manera óptima de apilarlas era mediante un arreglo piramidal de caras centradas.
 Diagrama de Strena seu de nive sexangula ilustrando la conjetura de Kepler. Fuente: Wikimedia Commons.
Diagrama de Strena seu de nive sexangula ilustrando la conjetura de Kepler. Fuente: Wikimedia Commons.
En la primavera de 2016 Maryna Viazovska anunció que había conseguido resolver un caso particular del problema de empaquetamiento de esferas, que generaliza en cualquier dimensión la conjetura de Kepler. Lo explicaba de esta manera en una entrevista concedida en 2017:
La pregunta es: ¿cuántas bolas de ocho dimensiones caben en un espacio de ocho dimensiones? Es decir, ¿con qué densidad se pueden empaquetar allí? […] En dimensión tres, este es el famoso problema de Kepler formulado ya en 1611. Se resolvió a finales del siglo XX con ayuda de computadoras. Existen innumerables maneras de colocar bolas tridimensionales, incluso con un ordenador es imposible verificar todos los casos. Pero surgió la idea de reducirlo a un cierto cálculo finito, aunque todavía muy largo y complicado. Es una historia bastante dramática. Un matemático anunció la solución, pero luego encontró muchos errores en ella. A principios de la década de 1990, otro científico de China hizo una declaración similar, pero también se encontraron muchos fallos. Y solo Tom Hales, después de pasar varios años, señaló la respuesta correcta en 1998. Se ha prestado una meticulosa atención a este trabajo, se ha revisado durante mucho tiempo, se ha revisado por pares durante cinco años, y se ha debatido si debiera considerarse como una solución matemática porque depende en gran medida de cálculos informáticos. Pero decidieron que todo era correcto. Y, recientemente, Hales también escribió una solución formal que se puede probar usando un programa de ordenador que, de hecho, está diseñado para validar tal evidencia. […] Resulta que hay una especie de atajo en el espacio de ocho dimensiones, por lo que podemos ir por un camino más fácil. En 2003, hubo novedades que indicaban que esto podía probarse. Me las arreglé para terminar este argumento de una manera lógica. Luego, trabajando con colegas, resolvimos el problema en dimensión 24.
En el artículo The sphere packing problem in dimension 8 Viazovska demostraba que el empaquetamiento óptimo de esferas de dimensión 8 era una configuración del espacio de ocho dimensiones denominada retículo E8. Su prueba involucraba una determinada función que Viazovska construía de manera explícita utilizando técnicas de teoría de números (formas modulares y casimodulares) y de análisis de Fourier.
Poco tiempo más tarde, junto a sus colaboradores habituales y el matemático Henry Cohn, resolvió el problema en dimensión 24. En este caso, esa configuración especial es el denominado retículo de Leech, que permite colocar 196 560 esferas de dimensión 24 tangentes a una esfera central. Tras el largo proceso que llevó a Viazovska a resolver el caso en dimensión 8, Cohn se dio cuenta de que la ingeniosa estrategia usada por Maryna podía utilizarse también en dimensión 24: en pocos días, este segundo caso se solucionó.
La medalla Fields llega en 2022La matemática iraní Maryam Mirzakhani (1977-2017) se convirtió en 2014 en la primera mujer en ganar la Medalla Fields, el prestigioso premio que otorga cada cuatro años la Unión Matemática Internacional (IMU) durante el Congreso Internacional de Matemáticos (ICM).
En 2018, Maryna Viazovska era una de las personas candidatas a recibirla, aunque tuvo que esperar otros cuatro años para que ese sueño se cumpliera. Es la segunda mujer que recibe este galardón; en los 86 años de existencia del premio, 62 hombres –aunque Grigori Perelman (1966) rehusó aceptarla en 2006– y dos mujeres han obtenido la Medalla Fields.
El gran mérito de Viazovska reside en haber sabido relacionar disciplinas muy distintas –el análisis de Fourier y la teoría de formas modulares– para descubrir “estructuras muy simples, naturales, profundas, cosas que nadie esperaba y que nadie más había podido encontrar”, como comentaba Henry Cohn en la laudatio que le dedicó durante el ICM para celebrar su trabajo.
La técnica descubierta por Viazovska para resolver el problema de empaquetamiento de esferas está estrechamente vinculada a las dimensiones 8 y 24. Para el resto de las dimensiones (mayores que 3) será necesario buscar nuevos métodos para encontrar esas configuraciones óptimas.
Como la propia Maryna Viazovska comenta, ella es una matemática teórica que desconoce la posible utilidad “práctica” (al margen de las matemáticas) de los objetos con los que trabaja. ¡Cuántas veces le habrán preguntado para qué sirven esas complejas estructuras que manipula!
El topólogo algebraico Jaume Aguadé escribía hace 30 años un hermoso artículo titulado Cien años de E8.; en él habla precisamente de las insólitas aplicaciones que poseen esas matemáticas que centran la investigación de Maryna Viazovska:
[…] ¿Para qué puede servir –se preguntará– empaquetar esferas de dimensión 8? Sirve para llamar por teléfono, para escuchar Mozart en un Compact Disc, para enviar un fax, para ver televisión vía satélite, para conectar, mediante un módem, con una red de ordenadores. Sirve en todos aquellos procesos en que se exija la transmisión eficiente de información digital. La teoría de la información nos enseña que los códigos de transmisión de señales son más fiables en dimensiones elevadas y el retículo de E8, con su sorprendente simetría y dada la existencia de un decodificador apropiado (Conway 1982), es un instrumento fundamental en la teoría de la codificación y transmisión de señales. […]
Referencias
-
Página personal, EPFL
-
Maryna Viazovska, The sphere packing problem in dimension 8, Ann. of Math. 185 (2017), no. 3, 991-1015
-
Henry Cohn, Abhinav Kumar, Stephen D. Miller, Danylo Radchenko and Maryna Viazovska, The sphere packing problem in dimension 24. Ann. of Math. 185 (2017), no. 3,1017-1033
-
Henry Cohn, The work of Maryna Viazovska, ICM 2022
-
Davide Castelvecchi, Ukrainian mathematician becomes second woman to win prestigious Fields Medal, Nature 607 (2022) 224-225
-
Davide Castelvecchi, ‘Mathematics is an unknown land’: meet Fields Medal winner Maryna Viazovska, Nature 607 (2022) 649
-
Thomas Lin and Erica Klarreich, In Times of Scarcity, War and Peace, a Ukrainian Finds the Magic in Math, Quanta Magazine, 5 julio 2022
-
Jaume Aguadé, Cien años de E8, La Vanguardia, 8 junio 1991
-
O’Connor, John J.; Robertson, Edmund F., Maryna Viazovska, MacTutor History of Mathematics archive, University of St Andrews
-
Francisco R. Villatoro, Medallas Fields 2022 para Maryna Viazovska, James Maynard, June Huh y Hugo Duminil-Copin, La ciencia de la mula Francis, 5 julio 2022
-
Wikipedia, Maryna Viazovska
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Maryna Viazovska, la matemática que empaqueta esferas se ha escrito en Cuaderno de Cultura Científica.
Einstein y la equivalencia masa-energía
E = mc2 es la ecuación más famosa del mundo. Dice que la energía es igual a la masa multiplicada por la velocidad de la luz al cuadrado. Pero Einstein no fue el primero en sugerir que existe una relación entre masa y energía. En 1905 los físicos ya sabían que la energía de un electrón le confería “masa electromagnética”. Así, J.J. Thomson en 1893 y Wilhem Wien en 1900 llegaron a la expresión m = (4/3) E/c2; Max Abraham (1902) y Hendrik Lorentz (1904) llegaron a expresiones similares. Einstein sí fue el primero en afirmar que esta equivalencia era una regla general, aplicable a todas las masas y no solo a casos especiales, que la energía puede “transportar” inercia, y que la masa puede “convertirse” en energía.
 A las 05:29 del 16 de julio de 1945 tenía lugar la demostración más terrorífica de la realidad de la equivalencia masa-energía: la detonación de la primera bomba atómica, nombre enclave para el Ejército de los Estados Unidos «Trinity».
A las 05:29 del 16 de julio de 1945 tenía lugar la demostración más terrorífica de la realidad de la equivalencia masa-energía: la detonación de la primera bomba atómica, nombre enclave para el Ejército de los Estados Unidos «Trinity».Einstein descubrió esta conexión a partir de un experimento mental partiendo de las ideas de la teoría especial de la relatividad. En la base de esta teoría está la afirmación de que las leyes de la física deben ser las mismas en cualquier marco de referencia, es decir, tanto si te estás moviendo como si estás quieto. Además, la teoría afirma que esas leyes son las mismas sin importar cómo sean percibidas desde cualquier otro marco de referencia. Einstein calculó que un cuerpo que emitiese luz, que es una forma de energía, al ser observado desde otro marco de referencia parecería estar perdiendo momento lineal. Mirándolo desde este marco de referencia la única explicación para esta pérdida de momento es que estuviese perdiendo masa. Dado que las leyes de la física deben ser iguales para todos los observadores (para todos los marcos de referencia) entonces, si esto es lo que está pasando en un marco de referencia, debe ser lo que está pasando en todos. Debe ser cierto que cuando un cuerpo pierde energía también está perdiendo masa, y la cantidad de masa que pierde está relacionada con la energía emitida por la expresión m = E/c2. Einstein escribió. “La masa de un cuerpo es una medida de su contenido en energía”.
De hecho E = mc2 es la versión simplificada de la ecuación completa, dado que se refiere solamente a la masa en reposo de un objeto, m0, la masa que contiene cuando está en reposo. Cuando un objeto se mueve se añaden términos adicionales y entonces la ecuación completa queda E2= (m0c2)2+ (pc)2, donde p es el momento lineal del objeto. Si el objeto está en reposo pes cero y obtenemos la versión simplificada.
Einstein descubrió la fórmula E = mc2porque las matemáticas le llevaron a ella. La ecuación de equivalencia entre masa y energía surge de forma natural del desarrollo matemático de leyes conocidas de la física. Pero Einstein sabía que su conclusión era asombrosa, y escribió una nota a su amigo Conrad Habitch. “No puedo saber si el querido Dios no se ríe de esto y me ha gastado una broma”. Además no estaba seguro si la idea podría comprobarse experimentalmente alguna vez. En el artículo en el que la daba a conocer sugería que quizás el estudio de la energía emitida durante la desintegración de las sales de radio podría ser una forma de probar su predicción.
La tecnología necesaria para medir con precisión los cambios en masa y energía simplemente no existía en 1905. La primera comprobación experimental de E = mc2no tuvo lugar hasta 1932 y se hizo por un método muy diferente. John Cockcroft y Ernest Walton eran dos físicos que trabajaban en los laboratorios Cavendish de Cambridge (Reino Unido). A principios de los años 30 del siglo pasado construyeron lo que era, en esencia, el primer acelerador de partículas y comenzaron a estudiar las colisiones entre ellas. Lanzaron protones a alta velocidad contra átomos de litio y estudiaron los resultados de la fisión: dos partículas alfa. El litio y el protón iniciales tenían más masa que las partículas alfa, pero éstas se movían mucho más rápido. Usando la última tecnología disponible, Cockcroft y Walton hicieron mediciones precisas y determinaron que la energía de las partículas alfa cuando se sumaba a su masa se correspondía con el valor de la energía más la masa del litio y protón originales. Por lo tanto, si bien la masa no se conservaba, la masa y la energía sí.
Un año después, en París (Francia) en 1933, Irène y Frédéric Joliot-Curie estudiaron el fenómeno en la dirección opuesta, cómo la energía se puede convertir en masa. Ese año, tomaron fotografías de partículas moviéndose a través de una cámara de niebla y demostraron cómo un fotón sin masa pasaba a ser partículas con masa y energía equivalentes a la cantidad de energía del fotón. La masa y la energía eran dos caras de la misma moneda.
Para saber más:
Gustave le Bon y la equivalencia masa-energía
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Una versión anterior de este artículo se publicó en Experientia Docet el 11 de julio de 2010.
El artículo Einstein y la equivalencia masa-energía se ha escrito en Cuaderno de Cultura Científica.
La evolución en mosaico de «Homo sapiens»
El estudio del genoma de nuestros parientes más cercanos, los neandertales y los denisovanos, ha abierto nuevas vías de investigación para comprender mejor nuestra historia evolutiva. Un estudio liderado por la Universidad de Barcelona ha estimado cuándo surgieron algunas de las variantes genéticas que caracterizan a nuestra especie a partir del análisis de mutaciones que son muy frecuentes en las poblaciones humanas modernas, pero no en estas otras especies de humanos arcaicos. Los resultados aportan nuevos indicios de la evolución en mosaico para nuestra especie. Además, muestran dos momentos en los que se concentran las mutaciones: uno temprano, de hace alrededor de 40.000 años, asociado al crecimiento de la población de Homo sapiens y su salida de África, y otro más antiguo, de hace más de 100.000 años, relacionado con la etapa en la que más tipos de Homo sapiens había en África.
«La comprensión de la historia profunda de nuestra especie es cada vez más completa. Aun así, es difícil determinar cuándo surgieron las variantes genéticas que nos distinguen de otras especies humanas. En este estudio hemos colocado variantes específicas de nuestra especie en una línea cronológica. Así, hemos descubierto de qué manera se concentran estas variantes en el tiempo, lo que ha reflejado eventos como el punto de divergencia del Homo sapiens respecto a otras especies humanas hace cerca de 100.000 años», explica Alejandro Andirkó, primer autor de este artículo, que ha surgido de su tesis doctoral en la UB.
 Imagen: Rob Mulally / UnsplashPredominio de variaciones relacionadas con la conducta y la anatomía facial
Imagen: Rob Mulally / UnsplashPredominio de variaciones relacionadas con la conducta y la anatomía facial
Los resultados de la investigación también muestran diferencias entre periodos evolutivos. En concreto, han constatado el predominio de variaciones genéticas relacionadas con la conducta y la estructura anatómica facial —características clave en la diferenciación de nuestra especie respecto al resto de las humanas— hace más de 300.000 años, una datación que coincide con la evidencia fósil y arqueológica disponible. «Hemos descubierto conjuntos de variantes genéticas que afectarían a la evolución de la cara y que hemos datado entre los 300.000 y los 500.000 años, justo el período anterior a la datación de los fósiles más tempranos de nuestra especie, como los descubiertos en el yacimiento arqueológico de Jebel Irhoud, en Marruecos», destaca Alejandro Andirkó.
Los investigadores también han analizado las variantes relacionadas con el cerebro, al que consideran el órgano que mejor puede ayudar a explicar las características clave del rico repertorio de comportamientos asociados con el Homo sapiens. En concreto, han datado variantes que se han relacionado con el volumen cerebral del cerebelo, el cuerpo calloso y otras estructuras en estudios médicos con humanos actuales. «Hemos descubierto que los tejidos cerebrales tienen un perfil de expresión genómica particular en distintos momentos de nuestra historia; es decir, ciertos genes relacionados con el desarrollo neuronal se expresaban más en ciertos momentos», resalta el investigador.
Reforzada la hipótesis de la evolución en mosaicoEstos resultados se complementan con una idea que es dominante en la antropología evolutiva hoy en día: que la historia de las especies humanas no es lineal, sino que distintas ramas de nuestro árbol evolutivo convivieron y muchas veces se cruzaron. «La amplitud del rango de diversidad de humanos en el pasado ha sorprendido a los antropólogos. Incluso dentro de los Homo sapiens existen fósiles, como los que he comentado antes de Jebel Irhoud, que debido a sus rasgos se llegó a pensar que pertenecían a otra especie. Por eso decimos que el ser humano ha vivido una evolución en mosaico», detalla Andirkó.
«Nuestros resultados —continúa el investigador— ofrecen una imagen de cómo cambió nuestra genética que se ajusta a esa idea, ya que no hemos encontrado evidencia de cambios evolutivos que dependieran de una mutación clave o de un puñado de ellas», subraya.
La metodología para llevar a cabo este estudio se ha basado en un método de estimación genealógica de edad de variantes (genealogical estimation of variant age) desarrollado por investigadores de la Universidad de Oxford. A partir de esta estimación, se ha aplicado una herramienta de aprendizaje automático para predecir qué genes han cambiado más en ciertos períodos y en qué tejidos estos genes pueden haber tenido un impacto mayor. En concreto, han utilizado ExPecto, una herramienta de aprendizaje profundo que usa una red convolucional —un tipo de modelo computacional— para predecir niveles de expresión de un gen y su función desde una secuencia de ADN.
«Como no existen datos sobre la expresión genómica de variantes en el pasado, esta herramienta es una aproximación a un problema que no se había podido responder hasta ahora. Aunque la predicción por aprendizaje automático es cada vez más común en el mundo clínico, que sepamos, no se había intentado usar para predecir las consecuencias de cambios genómicos a lo largo del tiempo», subraya Andirkó.
La importancia de la fase perinatal en el desarrollo del cerebro de nuestra especieEn un estudio previo, el mismo equipo de la UB, junto con el investigador Raül Gómez Buisán, también había utilizado la información genómica de los humanos arcaicos. Se trata de una investigación en la que analizaron los desiertos genómicos, regiones del genoma de nuestra especie donde no hay fragmentos genéticos de neandertales o denisovanos, y que, además, han sido sometidas a presión positiva en nuestra especie, es decir, que han acumulado más mutaciones de lo esperado por evolución neutral. Los investigadores estudiaron la expresión de genes —qué proteínas codifican para llevar a cabo diferentes funciones— hallados en estas regiones desérticas a lo largo del desarrollo del cerebro, desde fases prenatales hasta la etapa adulta, y cubriendo dieciséis estructuras cerebrales. Los resultados mostraron diferencias en la expresión génica del cerebelo, el cuerpo estriado y el tálamo. «Estos resultados ponen el foco en la relevancia de estructuras del cerebro más allá de la neocorteza, la cual ha sido tradicionalmente predominante en la investigación de la evolución del cerebro humano», explica Juan Moriano.
Además, las diferencias más notorias entre estructuras cerebrales se encontraron en las etapas prenatales. «Estas conclusiones suman nuevos indicios a la hipótesis de una trayectoria del desarrollo del cerebro específico de nuestra especie que tiene lugar en etapas perinatales —el período que comprende desde la semana 22 de gestación hasta las primeras cuatro semanas de vida neonatal—, lo que daría lugar a una forma más globular de la cabeza en los humanos modernos, en contraste con la forma más alargada en neandertales», concluye Juan Moriano.
Referencia:
Andirkó, A.; Moriano, J.; Vitriolo, A.; Kuhlwilm, M.; Testa, G., y Boeckx, C. (2022) Temporal mapping of derived high-frequency variants supports the mosaic nature of the evolution of Homo sapiens Scientific Reports doi: 10.1038/s41598-022-13589-0
Para saber más:
¿Qué factores han impulsado la evolución cognitiva en el linaje humano?
Edición realizada por César Tomé López a partir de materiales suministrados por la Universidad de Barcelona
El artículo La evolución en mosaico de «Homo sapiens» se ha escrito en Cuaderno de Cultura Científica.
Qué es y qué no es inteligencia artificial
Victor Etxebarria Ecenarro
 Detalle de «Ragazza de Trieste» de Joseph Ayerle. Muestra la imagen del rostro de la actriz Ornella Mutti tratada por una «inteligencia artificial» que ha sido entrenada para reproducir el estilo y las técnicas pictóricas que empleó Rafaello Sanzio (Rafael) (1483-1520) en su obra «La Fornarina» (1518/19). Fuente: Wikimedia Commons
Detalle de «Ragazza de Trieste» de Joseph Ayerle. Muestra la imagen del rostro de la actriz Ornella Mutti tratada por una «inteligencia artificial» que ha sido entrenada para reproducir el estilo y las técnicas pictóricas que empleó Rafaello Sanzio (Rafael) (1483-1520) en su obra «La Fornarina» (1518/19). Fuente: Wikimedia CommonsEn los últimos años el término inteligencia artificial y todo lo que tiene que ver con ello está adquiriendo un gran protagonismo y sobredimensionamiento. La expresión inteligencia artificial está siendo abusada y utilizada de forma básicamente incorrecta diariamente y en múltiples ámbitos cotidianos, desde el político al empresarial.
¿Existen realmente máquinas inteligentes, similares a las personas? Si respondemos a esta pregunta con cierto rigor, desde las bases de las ciencias fundamentales que soportan los pilares de este área –matemáticas y física–, la respuesta es que no. Y muchos científicos conjeturan y argumentan seriamente que probablemente nunca existirán.
Computar no es lo mismo que pensarPartamos de las áreas de conocimiento adyacentes a las matemáticas y la física que se expandieron desde los años 30 y 40 del siglo XX, como la ciencia de la computación, la electrónica, la automática o el propio área de inteligencia artificial. En el año 1937 vieron la luz dos publicaciones científicas de enorme importancia: la primera, Sobre los números computables, con una aplicación al Entscheidungsproblem del matemático Alan Turing, y la segunda, Análisis simbólico de relés y circuitos de conmutación, del matemático e ingeniero electrónico Claude Shannon. Estos trabajos fundaron la forma inicial de crear máquinas electrónicas capaces de computar, manejar información y manipular símbolos mediante programación algorítmica.Sin embargo, la inteligencia artificial, entendida como aquella que pretende replicar capacidades intelectuales similares a animales o personas (llamada inteligencia general o inteligencia fuerte) no se ha demostrado en absoluto. Esto es: no hay evidencia ni matemática, ni física, ni se conoce la existencia de ningún prototipo equivalente a las capacidades pensantes de un cerebro humano.
Decisión vs. elección
En 1966 el matemático y profesor de Ciencias de la Computación en el Instituto Tecnológico de Massachusetts (MIT) Joseph Weizenbaum creó en su laboratorio un programa llamado ELIZA capaz de realizar procesamiento de lenguaje natural.
Esta sencilla herramienta reconocía palabras clave en las frases del usuario para elegir una frase modelo de su base de datos con la que contestar.
ELIZA era capaz de entablar una conversación con seres humanos simulando a una psicóloga empática. Weizenbaum modeló su estilo de conversación como preguntas abiertas para animar a los pacientes a comunicarse más eficazmente con la terapeuta, y le sorprendió que su programa fuera tomado en serio por muchos usuarios.
A la vista de que gran número de admiradores consideraron el programa como verdadero precursor de las máquinas pensantes, el propio autor se vio obligado a dejar claro que consideraba esta interpretación totalmente errónea e intentó vehementemente corregir en sus intervenciones posteriores estas ideas.
Entre otros muchos escritos, Weizenbaum publicó en 1976 el libro El poder informático y la razón humana: del juicio al cálculo. Con él trataba de explicar al público en general su trabajo y sus consecuencias desde la filosofía de la ciencia, sin incluir turbadoras fórmulas matemáticas en el texto.
En el libro, el autor distingue entre las capacidades de los computadores y el razonamiento humano, y establece una distinción crucial entre decidir y elegir. Lo mismo que en la automática la decisión y control de un proceso industrial se implementa con un circuito o un computador como controlador programado de dicho proceso, Weizenbaum explica que decidir es una actividad computacional, algo que en última instancia puede programarse y, sin embargo, la elección es el producto del juicio, no del cálculo.
El papel de la mecánica cuánticaEn 1989, el físico, matemático y Premio Nobel en el año 2020 Roger Penrose publicó su influyente libro La nueva mente del emperador en el que demuestra que el pensamiento humano no es básicamente algorítmico.
A caballo entre las matemáticas, la filosofía de la ciencia y la física, el texto incorpora tanto demostraciones matemáticas como ilustradas discusiones de los famosos exámenes de inteligencia (como el test de Turing y el experimento de la habitación china). Además conjetura la posible necesidad de las leyes de la mecánica cuántica para poder explicar correctamente nuestras mentes.
La obra fue devastadora para la tradicional inteligencia artificial fuerte. Inspiró contestaciones de múltiples autores en diversas áreas de conocimiento, pero sus tesis no pudieron ser refutadas convincentemente.
Penrose avanzó aún más en sus ideas con el segundo de sus libros sobre la conciencia humana, publicado en 1994: Las sombras de la mente. En él incluye una propuesta detallada sobre cómo podrían implementarse esos procesos cuánticos en el cerebro.
Las nuevas conjeturas, en colaboración con la biología y la neurociencia médica sugeridas por Penrose, incluyen en particular el citoesqueleto de las neuronas. En concreto los microtúbulos, importantes componentes del citoesqueleto, son lugares plausibles para el procesamiento cuántico y, en última instancia, para la conciencia.
Estas ideas pueden perfectamente ser incorrectas, tal y como el propio Penrose argumenta. Muchos investigadores multidisciplinares en estos campos intentaron refutar parte de estas propuestas, pero actualmente siguen en vigor.
Sin inteligencia artificial a la vistaDesde un punto de vista global, sabemos que se han estudiado múltiples enfoques desde hace décadas para tratar de expandir la inteligencia artificial. Las redes neuronales, los sistemas expertos, la lógica fuzzy y en los últimos tiempos el deep learning y el big data han dado lugar a útiles herramientas para resolver problemas con fines específicos.
Estas herramientas pueden ser impresionantes, pero debemos tener muy claro que no nos hemos acercado al desarrollo de la inteligencia artificial general. La llamada inteligencia débil (o inteligencia estrecha) corresponde con las aplicaciones que hoy tenemos, pero las afirmaciones exageradas sobre sus éxitos, de hecho, dañan la reputación de la inteligencia artificial como ciencia.
En más de ochenta años de investigación en este área no se ha producido ninguna prueba firme de niveles humanos de inteligencia artificial general. Sabemos que los circuitos artificiales son incapaces de modelar los sistemas nerviosos incluso de los invertebrados más simples. Aún con computadores muy rápidos y con enormes bases de datos, confiar en que el razonamiento, la inteligencia y la conciencia surjan de alguna manera simplemente aumentando más y más la complejidad no parece más que un camino sin salida.
Las herramientas informáticas son muy útiles, pero aunque una máquina gane a los ajedrecistas profesionales o sea capaz de proponer un recurso legal buscando jurisprudencia en su gran base de datos, no es una máquina pensante. Es importante no banalizar, diferenciar entre herramientas tecnológicas y entes inteligentes, así como dejar a la ciencia seguir trabajando con rigor en esta apasionante materia.![]()
Sobre el autor: Victor Etxebarria Ecenarro es Catedrático de Ingeniería de Sistemas y Automática en la Universidad del País Vasco (UPV/EHU)
Este artículo fue publicado originalmente en The Conversation. Artículo original.
Para saber más:
Máquinas inteligentes (II): Inteligencia artificial y robótica
En el control de la inteligencia artificial nos jugamos el futuro
El séptimo ángel
El artículo Qué es y qué no es inteligencia artificial se ha escrito en Cuaderno de Cultura Científica.
CienciaClip 2021 – ¿Qué pasaría si el permafrost se derritiera en 24h?

Ciencia Clip es un concurso de vídeos divulgativos de ciencia diseñados, producidos y protagonizados por estudiantes de Educación Secundaria.
El objetivo del concurso es fomentar el interés por la ciencia y la tecnología. Y ofrecer a los concursantes una oportunidad para ejercitar su creatividad y habilidades comunicativas usando herramientas que proporciona internet.
Ciencia Clip es una iniciativa de la Cátedra de Cultura Científica de la UPV/EHU y en la que colaboran Euskampus Fundazioa, Naukas, Scenio y Big Van.
Los ganadores de la edición 2022 se anunciarán en la página web del concurso a principios de septiembre. La entrega premios y el anuncio del vídeo ganador del premio especial se realizarán durante el evento Naukas Bilbao. En la edición de 2021 resultó ganador en la categoría de 3º y 4º de la ESO Irene León, de Barcelona, con este vídeo:
Edición realizada por César Tomé López
El artículo CienciaClip 2021 – ¿Qué pasaría si el permafrost se derritiera en 24h? se ha escrito en Cuaderno de Cultura Científica.
Orriak
- « lehenengoa
- ‹ aurrekoa
- …
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- …
- hurrengoa ›
- azkena »

