¿Entendiendo la cuarta dimensión?
Flatland: A Romance of Many Dimensions –Planilandia: Una novela de muchas dimensiones– es una novela satírica publicada en 1884 bajo el seudónimo de A Square –Un cuadrado–. Su autor era en realidad Edwin Abbott Abbott (1838-1926).
 Portada de Flatland (sexta edición). Imagen: Wikimedia Commons.
Portada de Flatland (sexta edición). Imagen: Wikimedia Commons.La historia está narrada por un cuadrado que vive en un mundo bidimensional. Abbott critica la jerarquía social de la época victoriana mediante la descripción de las diferentes castas a las que pertenecen los habitantes de Planilandia. En este mundo, cada nueva generación nace con una arista más que la anterior. Las mujeres ocupan el lugar más bajo en la jerarquía –son simples líneas y no evolucionan–, les siguen los triángulos, los cuadrados, etc., subiendo de categoría social a medida que se añaden aristas a los polígonos. Los círculos –bueno, ‘casi’ círculos, son polígonos con ‘muchos’ lados– son los sumos sacerdotes…
Independientemente de la crítica social contenida en la novela, Planilandia es un texto que ayuda a entender y explicar los conceptos de múltiples dimensiones. En particular, el narrador –el cuadrado– llega a entender el concepto de dimensión tres cuando recibe la visita de una esfera tridimensional que atraviesa su mundo. Las diferentes secciones que genera la esfera al traspasar Planilandia son circunferencias que van creciendo de radio hasta llegar al ecuador, momento en el que las secciones circulares comienzan a disminuir hasta desaparecer.
Las siguientes tiras cómicas del ilustrador Rob Nance pueden ayudar a comprender mejor el anterior argumento. En este caso es Bucky –no es una esfera, pero es un ser de dimensión 3– quien llega a Planilandia. Varias figuras geométricas –triángulos, rectángulos, un hexágono y varios círculos– conversan en el bar Isósceles. Un cuadrado, con cigarrillo en la boca, entra y pide una cerveza. De repente, una enorme sombra invade el bar… un gigantesco pie aparece.
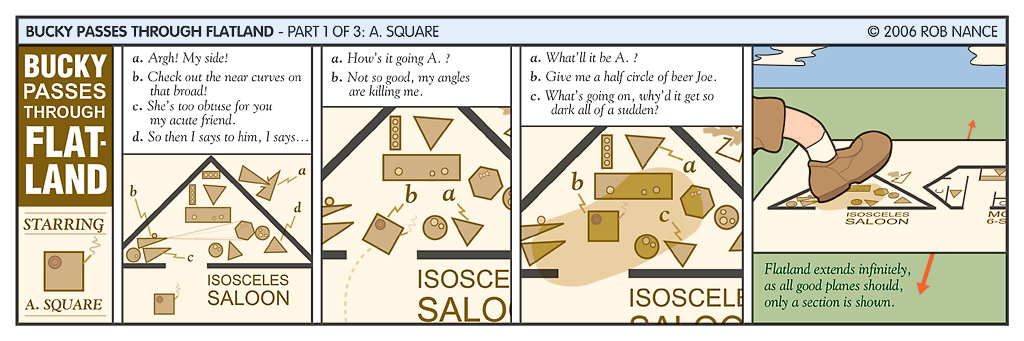 En el bar Isósceles (parte 1 de 3). © Rob Nance.
En el bar Isósceles (parte 1 de 3). © Rob Nance.Es el pie de Bucky que ha pisado varias figuras-clientes del bar: algunas se han roto, otras han reventado, un círculo se ha dividido en dos semicírculos, un rectángulo –el mostrador del bar– se ha partido en dos paralelogramos… Y lo más curioso del caso es que ha aparecido otro objeto: es circular, de color rosáceo y con un círculo central de color blanco. ¿Qué es? La última viñeta de esta tira lo aclara. Es la pierna de Bucky que ha atravesado Planilandia justo por encima del bar Isósceles. Ese objeto extraño de color rosáceo es la intersección de su pierna y el plano del bar –la carne es la parte rosácea y el hueso la porción blanca–.
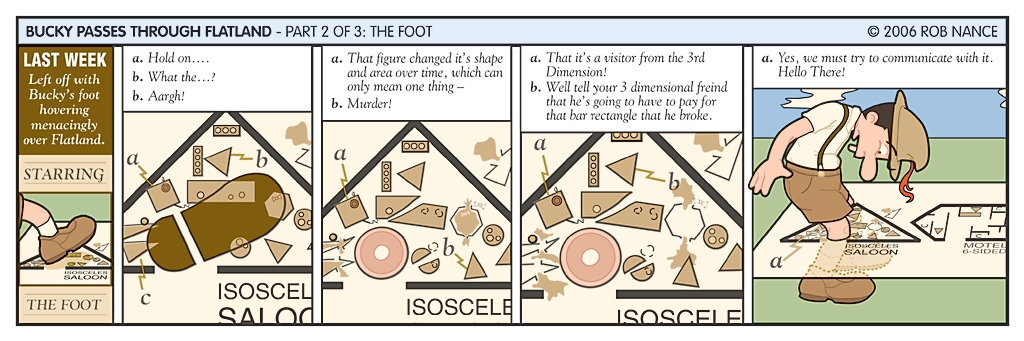 El pie de Bucky… y mucho más. © Rob Nance.
El pie de Bucky… y mucho más. © Rob Nance.El cuadrado increpa a Bucky, quien saca al polígono de cuatro lados del plano de Planilandia en el que vive… Bucky se lo come –el juego de palabras de ‘square meal’ no tiene sentido en castellano, cuya traducción sería ‘comida completa’– terminando de manera trágica –al menos para el cuadrado– la historia.
 El desenlace. © Rob Nance.
El desenlace. © Rob Nance.De manera análoga se puede explicar el concepto de dimensión 4: si un objeto de dimensión 4 estuviera cerca de nuestro mundo, no lo detectaríamos a no ser que nos atravesara. ¿Y cómo lo veríamos? Al ver pasar –como objetos de dimensión 3– las diversas secciones de su cuerpo en nuestro mundo. Esto ya lo explicaba Raúl Ibáñez en Hipercubo, visualizando la cuarta dimensión (y 2).
Por cierto, en esa cuarta dimensión podrían pasarnos cosas muy raras a unos simples habitantes de un mundo de tres dimensiones, como le sucede al pobre Gottfried Plattner en La historia de Plattner narrada por H.G. Wells…
Bonus
Flatland: The Movie (2007) es una película de animación, un corto inspirado en la novela de Edwin A. Abbott, en el que la protagonista es Hex –un hexágono que habita en Planilandia–, nieta de Arthur Square, que desea demostrar la existencia de la tercera dimensión. Al final del corto se alude a la posible existencia, incluso, de ¡una cuarta dimensión! Debajo puede verse el tráiler oficial.
Flatland2. Sphereland (2012) es la continuación de Flatland: The Movie. Han pasado veinte años y Hex es ahora es una científica. Este corto se basa, de nuevo, en la novela de Edwin A. Abbott y en Sphereland:A Fantasy About Curved Spaces and an Expanding Universe (1965) del físico Dionys Burger (1892-1987), una secuela de Flatland que continúa explicando la tercera dimensión a las criaturas que habitan en un mundo plano. En esta aventura aparecen incluso objetos fractales, como un Mandelbulb y otros objetos extraordinarios que provienen de universos de dimensiones arbitrariamente grandes… Debajo puede verse el tráiler oficial de esta extraordinaria aventura.
Para saber más:
Marta Macho Stadler, Flatland: The Movie, ZTFNews.org, 10 mayo 2013
Marta Macho Stadler, Flatland 2: Sphereland, ZTFNews.org, 12 mayo 2013
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo ¿Entendiendo la cuarta dimensión? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Cristalografía (14): Generación X

En el discurso que dio con motivo del aniversario de la Sociedad de Física de Berlín a comienzos de 1896 su presidente no se mostró demasiado ilusionado con el futuro de esta ciencia. Poco después, cuando conoció el descubrimiento que había realizado Wilhelm Röntgen, a la sazón en la Universidad de Würzburg, el 8 de noviembre del año anterior y que había publicado el 28 de diciembre, cuando su discurso ya estaba listo, mostró su entusiasmo porque este descubrimiento suponía que “los segundos cincuenta años de esta institución habían comenzado tan brillantemente como los primeros”.
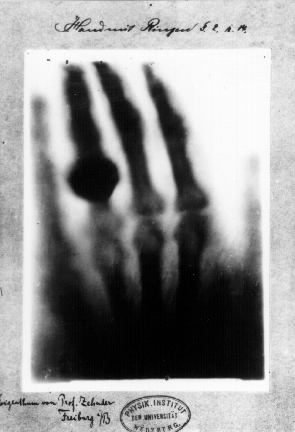
Su reacción fue representativa: desde el momento en que los científicos empezaron a tener noticia del descubrimiento de los rayos X, supieron que estaban ante un tónico revitalizante de una ciencia envejecida: suponía un reto para la teoría, incitaba a realizar nuevos experimentos, creó sensación entre el público general y le daba de golpe y porrazo a los médicos una nueva herramienta diagnóstica increíblemente potente. De hecho, hubo un tiempo, hasta que los médicos dispusieron de sus propios aparatos, en el que la gente que se tragaba un alfiler o recibía una perdigonada era derivada a los laboratorios de física para localizar estos objetos.
Los rayos X se resistían a ser clasificados en las categorías existentes. No se curvaban en presencia de campos magnéticos o eléctricos, por lo que no estaban constituidos por partículas cargadas; y, desde el momento en el que no se observaba reflexión o refracción, no parecían ser radiación electromagnética estándar. Muchos físicos empezaron a hablar de una nueva física en la que los rayos X eran una forma desconocida de radiación electromagnética. Sin embargo, las peculiaridades de los rayos X hacían que no terminasen de encajar con el concepto de onda,a pesar de la teoría que al respecto había desarrollado Arnold Sommerfeld. Así, por ejemplo, un tal William Henry Bragg, profesor en ese momento en la Universidad de Leeds, llamaba la atención sobre el hecho de que los rayos X eran capaces de suministrar a un electrón casi tanta energía como la empleada en la producción de los rayos; pero claro, razonaba WH Bragg, si los rayos X fuesen una onda tendrían que propagarse desde el punto de origen, difundiendo su energía, ¿cómo era posible entonces que una pequeña sección del frente de onda portase casi toda la energía original? Todo indicaba que los rayos X eran algún tipo de partícula desconocida. Y entonces llegó 1912.

El hijo de de WH Bragg, William Lawrence, fue con sus padres a la costa de Yorkshire a pasar sus vacaciones de verano. Lawrence se acababa de graduar en física y matemáticas con excelentes calificaciones en Cambridge y estaba en su primer año como investigador bajo la dirección de J.J. Thomson. Estando allí WH recibió una carta en la que se detallaba una conferencia espectacular dada por el físico teórico Max Laue. En ésta Laue daba cuenta de una observación hecha por sus colegas Walter Friedrich y Paul Knipping (los tres del departamento de Sommerfeld en la Universidad de Munich), una observación que hizo que WH se pusiese en pie de un salto y empezase a gritar llamando a su hijo: esos alemanes decían que habían comprobado la existencia de un patrón de difracción de rayos X en un cristal de sulfuro de cinc (ZnS): ¡los rayos X eran una onda! Se acabó la discusión sobre la naturaleza de los rayos X, aparentemente.

Padre e hijo no podían estar sin hacer nada con aquella información. Así que pasaron el resto del verano en el laboratorio de Leeds haciendo experimentos de difracción con rayos X como locos. En el viaje de vuelta a Cambridge al final de sus vacaciones, Lawrence no podía dejar de darle vueltas a los resultados que habían obtenido. Y al poco de llegar la idea revolucionaria había tomado forma: los resultados de Laue y sus colegas podrían interpretarse fácilmente con sólo suponer que se producían por la reflexión de los ratos X en los distintos planos atómicos del cristal. Lawrence fue un paso lógico más allá: la difracción de rayos X podía dar información a partir de la cual podría deducirse la disposición de los átomos en el cristal.
Para explicar los patrones que habían encontrado Laue et al habían asumido que la fuente de rayos X era policromática (en concreto que contenía 6 ó 7 longitudes de onda, no más) y que la estructura del ZnS consistía en una disposición tridimensional de pequeños cubos con los átomos de zinc y azufre ocupando vértices alternos.
Pero Lawrence examinó con detalle las fotografías de rayos X y se dio cuenta de que algunos puntos de difracción eran elípticos y que tenían diferentes intensidades. En un artículo leído por su supervisor, Thomson, ante la Sociedad Filosófica de Cambridge el 11 de noviembre de 1912, Lawrence hacía dos importantes propuestas para justificar estos hechos. Propuestas de un jovenzuelo de 22 años cuyas consecuencias están hoy en todos los libros de texto que traten la estructura de la materia y que le valdrían un Nobel con 25.
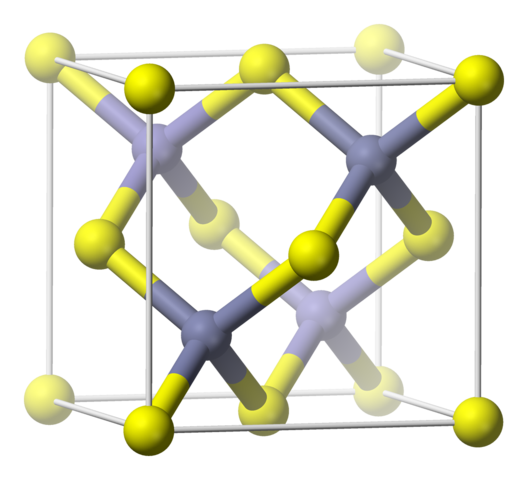
En primer lugar sugirió que los resultados de Laue et al eran la consecuencia de la reflexión de un continuo de longitudes de onda por los planos atómicos dentro del cristal. La cuantificación de esta idea le llevó a lo que hoy conocemos como ley de Bragg, a saber, nλ = 2d sen θ, donde θ es el ángulo de incidencia de los rayos X de longitud de onda λ, d es la separación de los planos reflectantes y n es un número entero. En segundo propuso que el patrón de difracción del ZnS era característico de átomos no sólo colocados en los vértices de una disposición tridimensional de cubos, sino también en las caras de dichos cubos: una red centrada en las caras.
Aquella conferencia fue el inicio de una reacción en cadena que llega hasta nuestros días. Y es que entre la audiencia estaba CTR Wilson. Pero de esto hablaremos en la próxima entrega.
No podemos terminar esta, sin embargo, sin nombrar a dos investigadores habitualmente olvidados en la historia de la difracción de rayos X que llegaron independientemente a resultados equivalentes a los de W Lawrence Bragg. Por una parte el teórico GV Wulf , de la Universidad de Moscú, derivó la ley de Bragg y la publicó en 1913.; y por otra Torahiko Tareda, de la Universidad de Tokyo, que como consecuencia de sus estudios con varios minerales, llegó a la conclusión de que los puntos de difracción obtenidos se correspondían a la reflexión de los rayos X en los distintos planos reticulares, algo antes que Bragg (su manuscrito, enviado antes desde Japón, alcanzó la redacción de Nature después de la conferencia de Thomson).
Referencias generales sobre historia de la cristalografía:
[1] Wikipedia (enlazada en el texto)
[3] Molčanov K. & Stilinović V. (2013). Chemical Crystallography before X-ray Diffraction., Angewandte Chemie (International ed. in English), PMID: 24065378
[4] Lalena J.N. (2006). From quartz to quasicrystals: probing nature’s geometric patterns in crystalline substances, Crystallography Reviews, 12 (2) 125-180. DOI:10.1080/08893110600838528
[5] Kubbinga H. (2012). Crystallography from Haüy to Laue: controversies on the molecular and atomistic nature of solids, Zeitschrift für Kristallographie, 227 (1) 1-26. DOI: 10.1524/zkri.2012.1459
[6] Schwarzenbach D. (2012). The success story of crystallography, Zeitschrift für Kristallographie, 227 (1) 52-62. DOI: 10.1524/zkri.2012.1453
Este texto es una revisión del publicado en Experientia docet el 13 de febrero de 2014
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Cristalografía (14): Generación X se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Formas moleculares de excreción de restos nitrogenados

Como apuntamos en la primera anotación de esta serie, la mayor parte de los animales eliminan sus restos nitrogenados a través de los sistemas de excreción y osmorregulación. En las anotaciones anteriores nos hemos ocupado de los mecanismos mediante los que esos sistemas producen la orina y la forma en que los tubos excretores mantienen los equilibrios hídrico y salino. Ha llegado el momento de referirnos de manera específica a las moléculas que se utilzan para eliminar los restos nitrogenados.
El metabolismo animal da lugar a la formación de productos tales como H2O y CO2. El agua metabólica pasa a formar parte de los elementos que intervienen en el balance hídrico, por lo que no ha de ser eliminada. El CO2, sin embargo, sí ha de ser expulsado, por las razones que expusimos en su día. Y el metabolismo de proteínas y ácidos nucleicos da lugar a la producción de restos nitrogenados.
Amonio
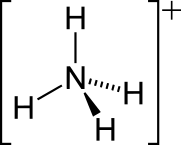
El producto terminal mayoritario del metabolismo de las sustancias nitrogenadas es el amoniaco (NH3), aunque en condiciones fisiológicas suele encontrarse en forma de ión amonio (NH4+). De hecho, lo más probable es que esta sea la molécula de excreción primitiva de los animales. Pero el amonio es una molécula muy tóxica. Entre otros efectos negativos, interfiere con el funcionamiento de la ATPasa de Na+/K+, lo que provoca una grave alteración de la integridad funcional de las membranas celulares. Esa es la razón por la que los efectos tóxicos del amonio se manifiestan, sobre todo, en el funcionamiento de las neuronas, que es muy dependiente de los fenómenos transmembrana. Concentraciones de amonio tan bajas como 2 mM en peces y 0,5 mM en mamíferos perjudican seriamente la función neuronal. Por esa razón el amonio ha de ser o bien eliminado o mantenerse muy diluido. Los animales acuáticos (en este caso ha de precisarse: animales que respiran en agua) no suelen tener mayores problemas. De hecho, no es raro que eliminen el amonio directamente a través de la pared corporal o de los epitelios branquiales. Así lo hacen la mayor parte de invertebrados marinos, peces teleósteos (tanto dulceacuícolas como marinos) y anfibios (larvas y adultos de vida acuática). A todos estos animales se les denomina amoniotélicos y a la forma de excreción, amoniotelismo.
Hay muy pocos animales terrestres que sean amoniotélicos, ya que para eliminar amonio hace falta mucha agua. De hecho, los pocos que eliminan amonio, o bien son animales de hábitats muy húmedos o lo hacen directamente en forma de NH3 gaseoso, como algunos isópodos terrestres. Algunos caracoles también, aunque no son amoniotélicos, eliminan parte de sus restos nitrogenados en forma gaseosa. Al parecer, esa forma de excreción está relacionada con la deposición de carbonato cálcico en el exoesqueleto.
Urea
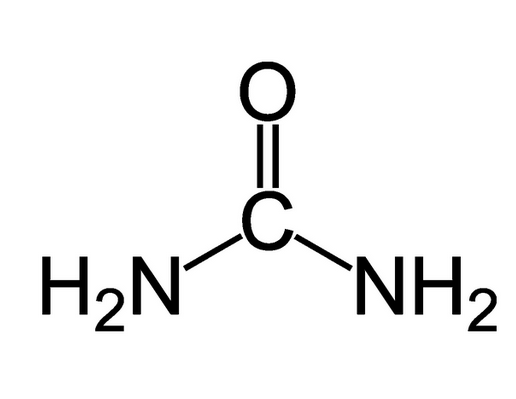
Otra molécula de excreción muy frecuente en el dominio animal es la urea. Es muy soluble y atraviesa con facilidad las membranas biológicas, aunque también tiene cierta toxicidad. De hecho, las concentraciones sanguíneas humanas se mantienen entre 3 y 7 mM, aunque pueden llegar a valores muy superiores. Por lo tanto, la excreción de restos nitrogenados en forma de urea necesita mucha menos agua que la excreción de amonio. En contrapartida, así como el amonio no requiere de un esfuerzo metabólico especial porque es el producto terminal que resulta de una secuencia de transaminaciones y desaminaciones de aminoácidos y sustancias similares, la urea ha de ser sintetizada y su síntesis requiere gasto de ATP (4 o 5 moléculas de ATP por molécula de urea). Este gasto es, pues, el coste que pagan los organismos que excretan sus restos nitrogenados en forma de urea a cambio de un importante ahorro de agua.
Ese ahorro explica el hecho de que la mayor parte de los animales que recurren a la urea como molécula mayoritaria de excreción sean vertebrados terrestres. Son ureotélicos los anfibios de vida adulta terrestre, algunas tortugas y todos los mamíferos. Sin embargo, apenas hay invertebrados que recurran al ureotelismo. Lo más probable es que este rasgo surgiera en los vertebrados que colonizaron el medio terrestre. Eso es lo que cabe deducir del hecho de que los peces de agua dulce –el grupo del que surgen los tetrápodos- sean mayoritariamente amoniotélicos. Del mismo modo, los anfibios terrestres transitan del amoniotelismo, característico de su fase larvaria acuática, al ureotelismo, propio de la vida adulta terrestre. La transición ocurre en paralelo a la metamorfosis y se produce al activarse –por efecto hormonal- la síntesis de las cinco encimas que catalizan las reacciones del ciclo de la urea. Los peces pulmonados y otras especies de peces también empiezan a sintetizar urea y dejan de producir amonio cuando se ven expuestos a estrés hídrico con carácter transitorio.
Como vimos aquí, además de ser usada como molécula de excreción, los condrictios y celacantos acumulan urea en su medio interno con fines osmóticos. Este dato indica que probablemente todos los vertebrados disponen de los genes necesarios para contar con un ciclo de la urea funcional; es la hipótesis que mejor explica el hecho de que la capacidad para sintetizar la molécula se encuentre tan extendida en este grupo y ocurra bajo circunstancias tan diversas.
Ácido úrico
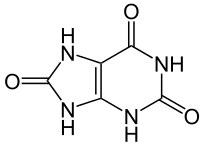
El ácido úrico y algunas formas químicas derivadas constituyen el tercer gran producto o grupo de productos de excreción de restos nitrogenados. Se suelen incluir en el grupo al ácido úrico, el ácido úrico dihidrato y los uratos, todas ellas purinas. Tienen una característica que las hace muy interesantes como moléculas de excreción: su baja solubilidad. Un litro de agua a 37ºC puede contener 0,4 milimoles de ácido úrico (lo que viene a ser 65 mg); por encima de esa concentración precipita. Por esa razón, en muchas ocasiones esas sustancias se eliminan en forma sólida o semisólida, de manera que se produce un gran ahorro de agua.
La baja solubilidad del ácido úrico es muy útil cuando un animal experimenta fuertes restricciones hídricas. Bajo esas circunstancias, en vez de aumentar su concentración, que es lo que ocurriría con la urea, una vez alcanzada la saturación, las cantidades adicionales precipitarían, acumulándose de forma sólida y, por lo tanto, evitando ejercer efectos tóxicos. Además del ácido úrico y los uratos, otras purinas, como la guanina o derivados del úrico, como la alantoína o el ácido alantoico, también son utilizados como molécula de excreción.
No hay acuerdo entre los especialistas acerca de los costes que conlleva la síntesis de ácido úrico. Algunos sostienen que son similares a los de la urea, aunque según otros pueden llegar a triplicar aquellos. No obstante, aunque la diferencia no llegue a ser tan importante, lo más probable es que, efectivamente, los costes sean mayores. Las ventajas que se derivan de su baja solubilidad, sin embargo, parecen compensar esa diferencia, por el gran ahorro de agua que conlleva su excreción. Eso explica que la mayor parte los animales terrestres sean uricotélicos. Lo son las aves, los lagartos, las serpientes, las tortugas que ocupan medios muy secos (ácido úrico), los arácnidos (guanina), la mayoría de insectos terrestres (ácido úrico, alantoína o ácido alantoico) y, en general, la mayoría de invertebrados terrestres.
Las reacciones metabólicas que posibilitan el uricotelismo son variantes de la vía de síntesis de las purinas, lo que explica el hecho de que hayan aparecido en tantos grupos animales. No está clara cuál es la razón por la que los mamíferos no son uricotélicos, aunque podría ser por la gran capacidad que han desarrollado para concentrar la orina en la urea gracias a su excepcional nefrona. Ello les permite un importante ahorro de agua a pesar de todo.
Para terminar, conviene reparar en el hecho de que todos los animales uricotélicos tienen desarrollo cleidoico, por lo que la posibilidad de almacenar úrico de forma sólida en el interior del huevo ha podido ser un factor determinante para la aparición del uricotelismo.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Formas moleculares de excreción de restos nitrogenados se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:La enmarañada historia de los cerdos

Si dejamos a los canes a un lado, los primeros animales domesticados fueron muflones asiáticos y cabras de Beozar, hace unos once mil años, jabalíes, hace unos diez mil quinientos, y uros, quinientos después. Todos ellos fueron domesticados en el norte del Creciente Fértil, en una zona que se superpone aproximadamente al actual Kurdistán.
El jabalí procede de las islas del Sudeste Asiático y a partir de su zona de origen se expandió por toda Eurasia. Hasta hace pocos años toda la información con la que contábamos sobre su origen, distribución y domesticación procedía de estudios arqueológicos. A partir de esos estudios se habían identificado dos focos de domesticación, uno en el Extremo Oriente, en China, y el otro en Oriente Próximo, en la zona geográfica en la que se domesticaron las especies antes citadas.
Sin embargo, gracias al espectacular desarrollo de las técnicas de genética molecular, se han podido obtener abundante información acerca de los linajes genéticos a los que pertenecen las variedades de cerdos existentes en la actualidad. Además, la secuenciación de ADN antiguo a partir de restos óseos ha permitido establecer relaciones entre los linajes identificados en los cerdos actuales y los de diferentes lugares de Eurasia en periodos anteriores.
El panorama que dibujan estos estudios es mucho más complejo. Y si bien se sigue aceptando que hubo dos focos principales, hay especialistas que proponen la existencia de hasta siete episodios de domesticación independientes en los albores del Neolítico y los milenios inmediatamente posteriores. La mayor parte, quizás hasta cuatro, de esas domesticaciones independientes se habrían producido en Oriente Próximo, otras dos en China, y el resto en otros lugares de Eurasia.
Los cerdos llegaron a Europa de la mano de pueblos que, procedentes del Creciente Fértil, expandieron la agricultura y la ganadería hasta nuestro subcontinente. Y aunque no es seguro, es posible que en Europa también se domesticasen jabalíes autóctonos y que estos acabasen sustituyendo parcialmente a los linajes procedentes de Asia. Aunque resulte paradójico, los cerdos que hay en Oriente Próximo en la actualidad no proceden de los que fueron domesticados allí originariamente. Como es sabido tanto el Judaísmo como el Islam prohíben el consumo de cerdo, tabú que quizás surgió en el antiguo Egipto y se extendió posteriormente hacia Israel y la Península Arábiga.
La cría del cerdo tuvo un gran éxito también en Asia, por donde se extendió, principalmente a partir de las variedades criadas en China. Desde el Extremo Oriente y el Sudeste asiático también se expandieron hacia la Polinesia. Los chinos seleccionaron cerdos muy prolíficos, hasta tal punto que en los siglos XVIII y XIX se importaron a Europa ejemplares de la variedad Meishan, procedentes del sur de ese país. Los cerdos europeos actuales tienen en parte ascendencia china por esa razón.
Es difícil identificar con precisión los linajes presentes en la actualidad en las diferentes variedades de cerdos que hay en el Mundo. Más difícil aún es atribuir el origen de esos linajes a ubicaciones geográficas y momentos concretos. Pudo haber varios episodios de domesticación al comienzo del Neolítico y quizás ocurrieron en lugares diferentes; además, ha podido haber domesticaciones posteriores. Por otro lado, no ha dejado de haber cruzamientos entre ejemplares salvajes y domesticados, por lo que ha habido un flujo genético permanente entre jabalíes y cerdos hasta que la estabulación plena lo ha limitado o impedido. Durante siglos los cerdos han vivido en relativa libertad en fincas y dehesas, o se han mantenido en corrales de no muy difícil acceso. Y es que tampoco para los gorrinos ha tenido puertas el campo.
—————————————————————–
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
————————
Una versión anterior de este artículo fue publicada en el diario Deia el 15 de julio de 2018.
El artículo La enmarañada historia de los cerdos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Javier S. Burgos: “Frankenstein siempre ha estado vivo”
Fue en verano de 1816, un verano tan gélido en Europa que más bien parecía invierno, cuando el poeta inglés Lord Byron, su médico personal, John Polidori, y sus amigos escritores Percy y Mary Shelley coincidieron en una villa suiza.
El rigor meteorológico impedía las actividades al aire libre así que los cuatro pasaron horas y horas leyendo y compartiendo sus vastos conocimientos en temas tan apasionantes y variados como las novelas de terror, la neurociencia o las teorías sobre la generación de electricidad cerebral de Luigi Galvani. Los experimentos de Galvani dieron lugar a numerosos y macabros ensayos en los que se trataba de reanimar cadáveres a través de la aplicación de corrientes eléctricas.
En ese escenario, tan oscuro como fascinante, Lord Byron propuso el reto de que los cuatro amigos escribieran una historia de miedo y Mary Shelley alumbró nada más y nada menos que Frankenstein. Una obra de ficción plagada de referencias científicas, que aborda una de las grandes obsesiones de la medicina: la generación de la vida.
 Imagen: Javier S. Burgos, director de la Fundación para la Investigación del Hospital Universitari i Politècnic La Fe de València, durante su charla en Naukas Bilbao 2018. (Fotografía: Iñigo Sierra)
Imagen: Javier S. Burgos, director de la Fundación para la Investigación del Hospital Universitari i Politècnic La Fe de València, durante su charla en Naukas Bilbao 2018. (Fotografía: Iñigo Sierra)Esta historia fue el punto de partida con el que el neurocientífico Javier S. Burgos inició su charla en la última edición de Naukas Bilbao, una intervención en la que repasó las tentativas del ser humano por devolver el aliento a los órganos inertes.
“La ciencia siempre ha querido generar vida donde no la hay. El concepto de que la ciencia pueda crear vida siempre ha estado encima de la mesa”, aseguró Burgos durante el evento de divulgación científica, celebrado entre el 13 y el 16 de septiembre en el Palacio Euskalduna de Bilbao.
Pero desde la atmósfera romántica en la que escribió su novela Mary Shelley a la actualidad han pasado muchas cosas. ¿Se sigue ocupando la ciencia moderna de crear vida? La respuesta es afirmativa.
Desfibriladores, marcapasos, exoesqueletos, prótesis, cultivos celulares para la obtención de nuevos tejidos, órganos artificiales, tejidos biónicos o trasplantes de órganos vitales. El experto demostró que el espíritu del doctor Frankenstein está más vivo que nunca, aunque la ciencia todavía se enfrenta con dificultades a los enigmas del misterioso sistema nervioso central.
“Excepto el cerebro, hemos conseguido la sustitución de los órganos mediante trasplantes”, aseguró Burgos.
En opinión del experto esa posibilidad, la de llevar a cabo el trasplante de un cerebro completo, es más que remota, por más que algún científico haya manifestado su intención de conseguirlo. Así que aunque haga un verano frío y les de por leer historias de terror, absténganse de hacer experimentos en casa.
Sobre la autora: Marta Berard, es periodista, responsable de contenidos de la agencia de comunicación GUK y colaboradora de la Cátedra de Cultura Científica de la UPV/EHU.
El artículo Javier S. Burgos: “Frankenstein siempre ha estado vivo” se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Polímeros biocompatibles para integrar dispositivos electrónicos en nuestro cuerpo
“En el campo de la bioelectrónica existe la necesidad de crear una nueva generación de materiales con propiedades mecánicas blandas, conductividad iónica y electrónica, y compatible con los tejidos biológicos”, indica Isabel del Agua López autora del estudio. El polímero conductor más exitoso en aplicaciones bioelectrónicas hoy en día es el PEDOT (poli 3,4-etilendioxitiofeno), comúnmente dopado con PSS (Poli(3,4-etilendioxitiofeno)-poli(estireno sulfonato)) dada su gran conductividad tanto electrónica como iónica, su biocompatibilidad, así como la estabilidad, etc.
Actualmente, “el PEDOT se comercializa dopado con PSS, pero uno de los inconvenientes es que así no es biofuncional. Por este motivo, para mejorar su biocompatibilidad este estudio se ha centrado en la fabricación de nuevos materiales de PEDOT estabilizado con polisacáridos como la goma xantana y la goma guar en lugar de con PSS, con el fin de que el material se integre mejor en nuestros tejidos”, explica del Agua López.
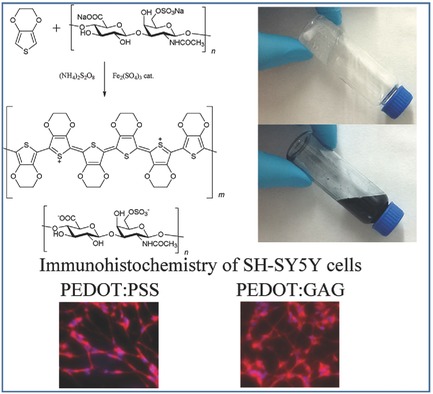
Partiendo de las combinaciones PEDOT:polisacárido que han sido realizadas en este trabajo por primera vez, se han creado dos nuevos materiales. Por un lado, los geles iónicos de PEDOT, que son únicos ya que nunca antes se había fabricado un gel iónico que a su vez contuviese PEDOT. “Este material presenta propiedades únicas que surgen de la combinación de materiales del que está hecho. Presenta conductividad electrónica dada por el PEDOT, conductividad iónica por el líquido iónico y la elasticidad impartida por el polisacárido goma guar”, explica la investigadora de la UPV/EHU. En general, “este material supera a los hidrogeles de PEDOT que ya existen, ya que no se seca, es más estable y no pierde ni sus propiedades mecánicas ni su conductividad”, añade. En la actualidad se están investigando sus propiedades y aplicaciones en bioelectrónica entre las que destaca su uso como electrodos cutáneos para electrofisiología. Sobre la piel, estos materiales transmiten la actividad eléctrica de nuestro cuerpo a los electrodos para su registro. Así se consigue registrar, por ejemplo, la actividad de nuestro corazón (electrocardiografía) o la de nuestros músculos (electromiografía).
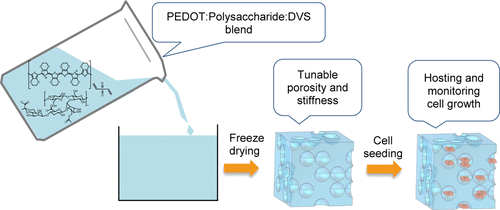
Por otro lado, “el segundo material que hemos fabricado —señala del Agua López— a partir de la combinación de PEDOT:polisacárido son las estructuras tridimensionales porosas denominadas scaffolds que sirven de soporte para el crecimiento tridimensional de células y formación de tejidos”. Gracias al contenido del polisacárido y a sus poros interconectados, las células presentan una especial afinidad por estos andamios. “Se ha demostrado que tanto la porosidad como las propiedades mecánicas de estos materiales se pueden modificar muy fácilmente dependiendo de la aplicación para la que se los quiere usar. Variando el contenido de PEDOT y de polisacárido los poros pueden tener mayor o menor diámetro y el andamio en su conjunto ser más blando o más duro”, indica. “El desarrollo de scaffolds basados en PEDOT pretende no solo facilitar el crecimiento celular sino también controlarlo”, añade Isabel del Agua.
A la vista de los resultados obtenidos, “las propiedades únicas de estos materiales poliméricos pueden llevar al campo de la bioelectrónica hacia nuevas aplicaciones, ya que estos materiales consiguen integrar dispositivos electrónicos con nuestro cuerpo e incluso a mejorar las aplicaciones actuales”, subraya la autora del trabajo.
Referencias:
Mantione, D. , del Agua, I. , Schaafsma, W. , Diez‐Garcia, J. , Castro, B. , Sardon, H. and Mecerreyes, D. (2016) Poly(3,4‐ethylenedioxythiophene):GlycosAminoGlycan Aqueous Dispersions: Toward Electrically Conductive Bioactive Materials for Neural Interfaces. Macromol. Biosci. doi:10.1002/mabi.201600059
Isabel del Agua, Sara Marina, Charalampos Pitsalidis, Daniele Mantione, Magali Ferro, Donata Iandolo, Ana Sanchez-Sanchez, George G. Malliaras, Róisín M. Owens, and David Mecerreyes (2018) Conducting Polymer Scaffolds Based on Poly(3,4-ethylenedioxythiophene) and Xanthan Gum for Live-Cell Monitoring ACS Omega doi: 10.1021/acsomega.8b00458
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Polímeros biocompatibles para integrar dispositivos electrónicos en nuestro cuerpo se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Sin moda no hay futuro

Soy periodista especializada en moda. Me licencié en periodismo, cursé un máster en moda y posteriormente me doctoré. Empecé a publicar mis artículos en conocidas revistas de moda mientras hacía mi tesis doctoral. Para obtener el doctorado era imprescindible tener al menos un artículo publicado en alguna de las revistas de más impacto del momento, o al menos, varios artículos en revistas medianamente buenas y reconocidas dentro del sector.
Por aquel entonces, mientras hacía el doctorado, yo disfrutaba de una beca estatal. Era una beca insuficiente, apenas me permitía hacer frente al alquiler, así que en ocasiones tuve que pedir ayuda a mi familia y compaginarlo con trabajos que poco tenían que ver con la moda. Todo muy precario. El gobierno nos había dado financiación a un grupo de periodistas para llevar a cabo un proyecto de investigación en moda. Con ese dinero hacíamos toda nuestra labor investigadora y cubríamos los gastos que generaba, desde la asistencia a la Fashion Week de Madrid, Milán o París, cosa que era todo un logro curricular, a todos los materiales que necesitásemos para llevar con éxito la investigación. Finalmente conseguí mi ansiado doctorado.
Yo tenía muy claro que quería seguir trabajando como periodista de moda. Desgraciadamente es un mundo muy competitivo y que destaca por la precariedad laboral, especialmente para jóvenes y para mujeres, y yo era ambas cosas. Pero mi sueño era seguir en el mundo de la moda. La moda es súper importante, todo el mundo lo sabe.
Conseguí seguir investigando en moda. Estuve trabajando en universidades públicas, en centros de investigación, incluso hice varias estancias en el extranjero. Puse todo mi empeño en ello y tuve que sortear obstáculos muy complicados durante años, sobre todo largos periodos de incertidumbre, poca estabilidad laboral, y un bajo nivel de ingresos. Todo lo hice por la moda.
La concesión de becas gubernamentales y financiación depende en gran medida de la calidad de las revistas de moda para las que escriba y de la cantidad de veces que mis artículos sean citados por otros compañeros de profesión en sus respectivos artículos. Cuantas más veces publique en revistas como Vogue, Harper’s Bazaar, Elle o InStyle, más opciones tengo de seguir en esto de la moda. Y cuantas más veces se citen esos artículos, más prestigio tendré dentro del mundo de la moda y, por tanto, más probabilidades de seguir viviendo de esto y de obtener financiación.
Por eso, en cuanto escribo un artículo sobre moda que creo que puede ser suficientemente bueno para alguna de estas revistas, lo envío. Estas revistas son empresas privadas. Se encargan de reenviar mi artículo a otros periodistas especializados en moda que revisan la calidad de mi trabajo y evalúan si, efectivamente, se trata de un artículo que merece ser publicado. Pueden ocurrir tres cosas, que acepten el artículo tal cual, que lo rechacen, o que lo acepten con correcciones. Es decir, los revisores trabajan como editores. Como la moda es súper importante, estos editores no cobran a las revistas por hacer su trabajo de revisión de artículos. Revisar artículos gratis es algo que todos hacen por el buen funcionamiento de la moda.
Si la revista acepta el artículo, fenomenal. Si no, pues pruebas con otras revistas menos conocidas, a ver quién lo quiere. También puedes pagarles para que lo publiquen. De lo que se trata es de publicar.
Las revistas tampoco nos pagan por nuestros artículos. Investigamos sobre moda y todo lo que sale de ahí se lo damos a las revistas de forma gratuita. De hecho, muchas revistas incluso nos cobran por publicar. Lo hacen porque pueden, porque mi sueldo depende de lo que yo haya publicado. Ningún organismo público financiaría mis investigaciones en moda si luego no se publican en las revistas. Así que hay revistas que llegan a pedir varios miles de euros a cambio de publicar tu trabajo. Se destina el dinero público no solo a la moda en sí, si no a publicar, y a veces esto representa un porcentaje muy alto de los fondos del proyecto.
En los años 90 estas revistas al menos hacían el trabajo de maquetación y diseño del artículo. Ahora no hacen ni eso. Somos los propios periodistas de moda los que tenemos que adaptarnos a un manual de estilo y entregar el artículo tal cual como aparecerá en la revista, incluyendo fotografías e infografías. Ahora muchas de ellas ni siquiera hacen distribución en papel. Eso sí, la suscripción a estas revistas, aunque solo existan online, sí te la cobran y es muy cara, pero claro, para cualquier periodista especializado en moda como yo es fundamental estar al tanto de todas las tendencias y de todo lo que se cuece en el mundo de la moda. Así que, o bien se paga individualmente por cada artículo que quiera leer, o bien la institución en la que trabajo paga la suscripción para que todos tengamos acceso a ella. Es decir, para acceder a la revista que haya publicado mi artículo, también tengo que pagar. Y cualquier otra persona que quiera comprarse la revista, obviamente también tendrá que pagarla de su bolsillo.
Estas revistas tienen unos ingresos anuales superiores a 22 mil millones de euros y un margen de beneficios cercano al 40%, muy superior al de Apple, Google o Amazon. No es de extrañar, porque es un negocio redondo.
En el caso de España se negocia una licencia nacional y por ejemplo, simplemente para que las universidades y los centros de investigación puedan estar suscritos a la Vogue, el coste para nuestras arcas públicas asciende a 24 millones de euros al año.
Los gobiernos son clientes cautivos de estas revistas. Y si quieres ser un país realmente puntero en el mundo de la moda, tienes que estar suscrito y pagar el acceso a ellas con fondos públicos. Sin embargo, no todos los gobiernos pueden pagarlo. Como en el caso de Perú, que no ha renovado la suscripción a la Vogue desde el año pasado. Por ese motivo surgieron repositorios piratas de artículos y es común que algunas personas compartan sus claves de acceso a las revistas online. La suscripción a la Vogue es cada año más cara, igual que la de InStyle o Harper’s Bazaar, y no todas las instituciones pueden costear la suscripción a todas ellas.
Así es como funciona la moda. Y la moda hay que hacerla.

Sobre la autora: Déborah García Bello es química y divulgadora científica
El artículo Sin moda no hay futuro se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:‘Imago mundi’, finalmente 9 retratos más del mundo
Con esta entrada termina la serie Imago Mundi de la sección Matemoción del Cuaderno de Cultura Científica, que hemos dedicado a mostrar diferentes retratos del mundo, realizados con diferentes proyecciones cartográficas (matemáticas). En la primera entrega, ‘Imago mundi’, 7 retratos del mundo, las 7 proyecciones cartográficas utilizadas fueron: la proyección cilíndrica conforme de Mercator, la proyección pseudo-cilíndrica isoareal de Mollweide, la proyección pseudo-cilíndrica isoareal de Eckert IV, la proyección isoareal interrumpida homolosena de Goode, la proyección convencional de Van der Grinten, la proyección central, que preserva los caminos más cortos, y la proyección estereográfica, que es conforme.
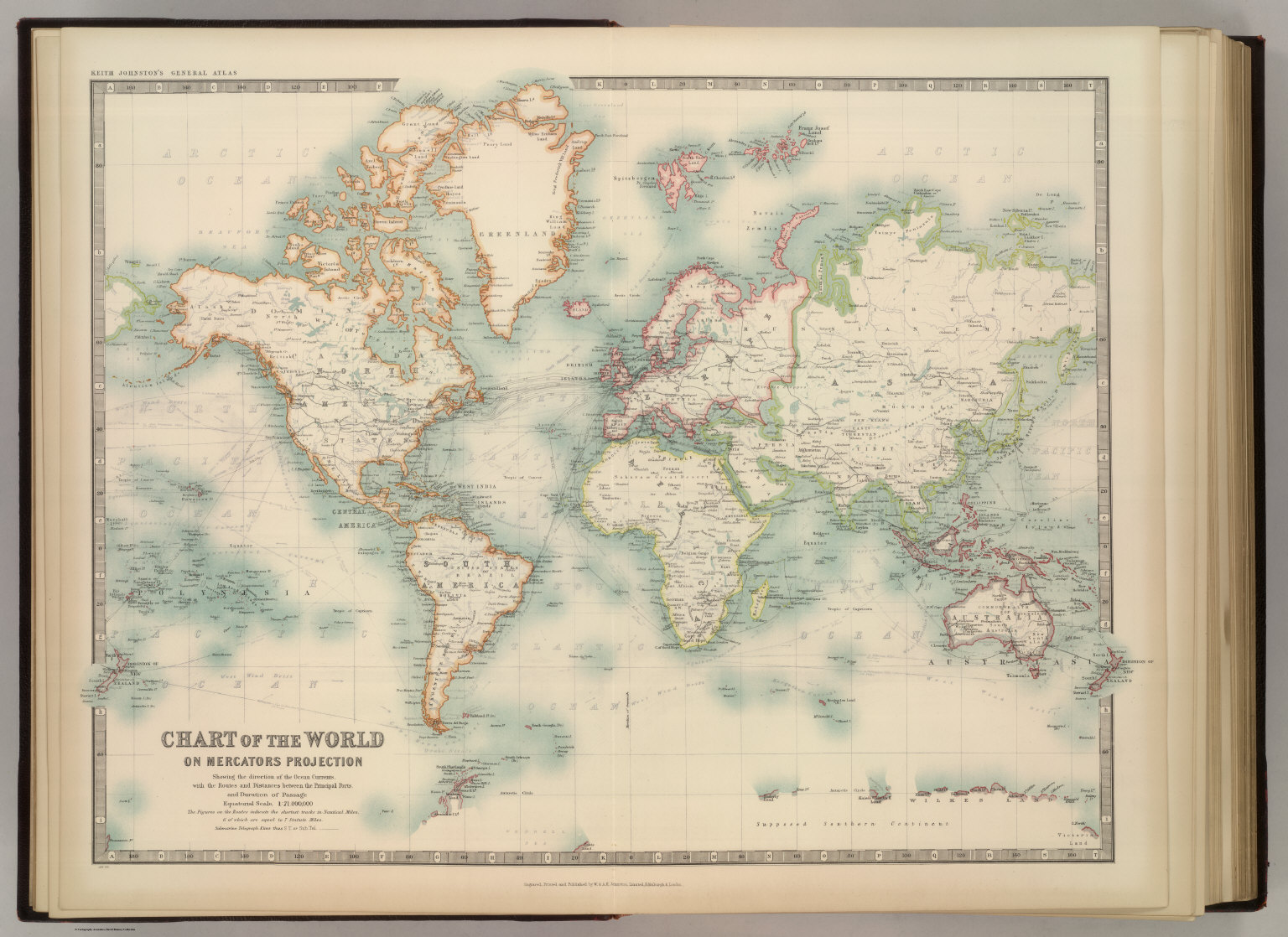 Mapa de mundo realizado con la proyección de Mercator, mostrando las corrientes oceánicas, así como las rutas y distancias entre los puertos más importantes, perteneciente a la publicación “The Royal Atlas Of Modern Geography Exhibiting”, W.& A.K. Johnston, 1912. Imagen de [1]Mientras que, en la segunda entrega, ‘Imago mundi’ 2, otros 6 retratos del mundo las proyecciones eran: la proyección rectangular o carta plana, la proyección cilíndrica de Miller, la proyección de Gall-Peters, con toda la familia de proyecciones cilíndricas isoareales a la que pertenece esta, la proyección de Robinson, la proyección de Winkel tripel y la proyección acimutal equidistante.
Mapa de mundo realizado con la proyección de Mercator, mostrando las corrientes oceánicas, así como las rutas y distancias entre los puertos más importantes, perteneciente a la publicación “The Royal Atlas Of Modern Geography Exhibiting”, W.& A.K. Johnston, 1912. Imagen de [1]Mientras que, en la segunda entrega, ‘Imago mundi’ 2, otros 6 retratos del mundo las proyecciones eran: la proyección rectangular o carta plana, la proyección cilíndrica de Miller, la proyección de Gall-Peters, con toda la familia de proyecciones cilíndricas isoareales a la que pertenece esta, la proyección de Robinson, la proyección de Winkel tripel y la proyección acimutal equidistante.
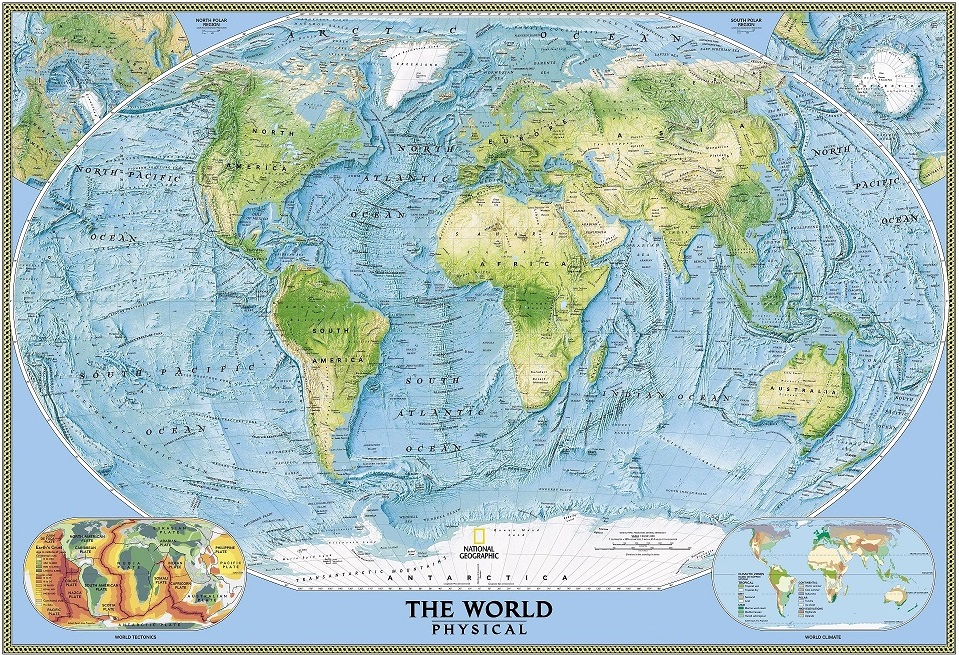 Mapa físico del mundo de National Geographic, realizado con la proyección de Winkel tripel, en 2005, revisado en 2007
Mapa físico del mundo de National Geographic, realizado con la proyección de Winkel tripel, en 2005, revisado en 2007Pero vayamos directamente a los retratos de esta tercera, y última, entrega de la serie.
Retrato 1: La proyección en perspectiva general
Si preguntáramos a la gente por la forma correcta de representar la superficie terrestre en un plano, muchas personas nos dirían que es realizando un retrato, o fotografía, desde un punto cualquiera del espacio. Esta es la conocida como proyección en perspectiva general.
La proyección en perspectiva general es una proyección geométrica azimuthal, que consiste en proyectar la superficie de la Tierra sobre un plano desde un punto de proyección mediante las rectas o “rayos” de proyección, es decir, como si estuviesemos mirando desde ese punto. Dependiendo de la posición del plano de proyección hablamos de perspectiva vertical o inclinada. La perspectiva es vertical si el plano es perpendicular a la recta que une el punto de proyección con el centro de la superficie terrestre, en otro caso, es inclinada.
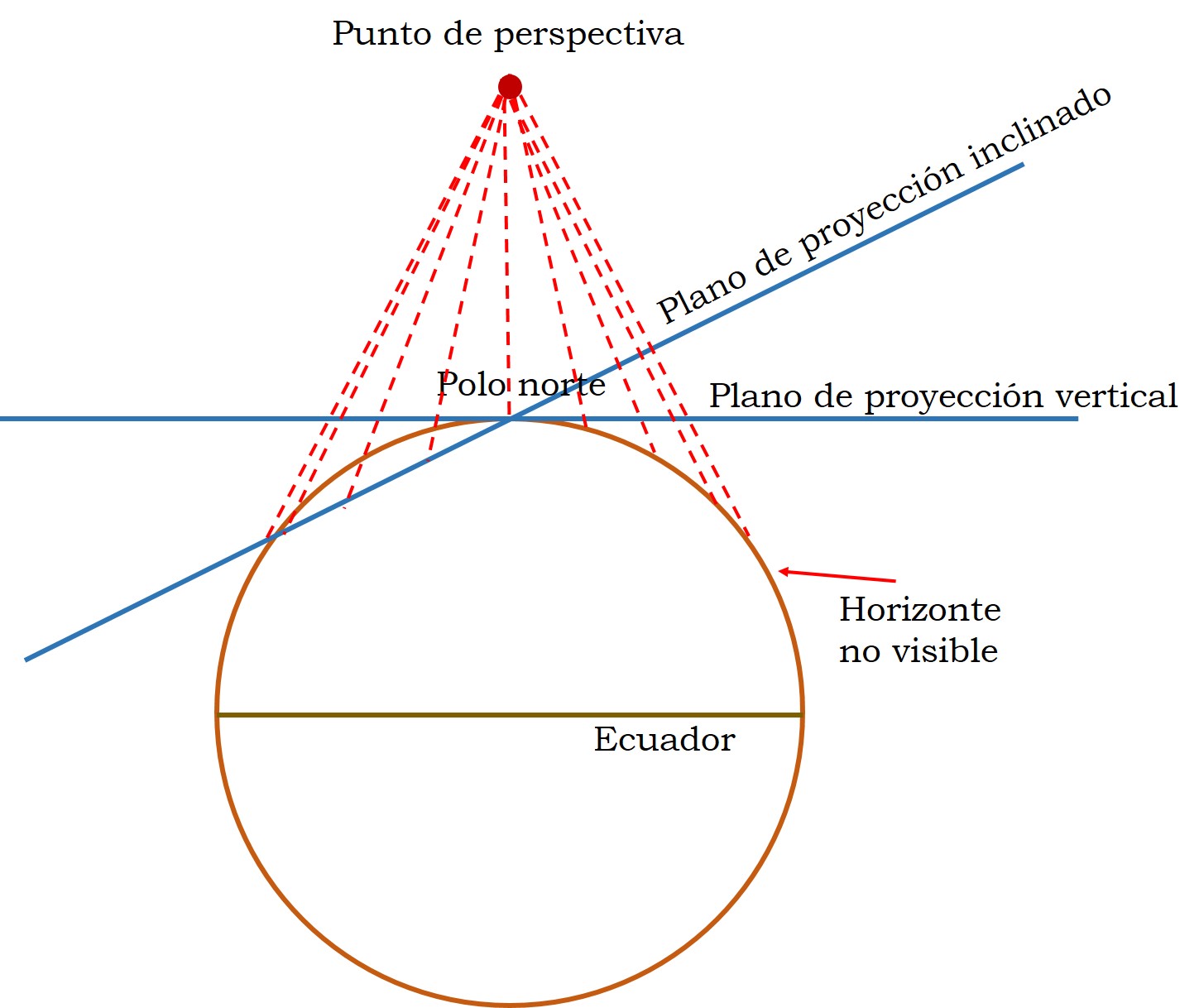 Esquema de la proyección en perspectiva general, verical o inclinada, desde un punto que está en la vertical del polo norte
Esquema de la proyección en perspectiva general, verical o inclinada, desde un punto que está en la vertical del polo norte
Dependiendo de lo lejos que esté el punto de proyección la imagen será más amplia o más reducida.
 Mapas realizados con la proyección en perspectiva vertical, con imágenes reales del proyecto “The Blue Marble New Generation” de la NASA, con el centro de proyección sobre el Ecuador, cerca de la desembocadura del río Amazonas, y con el punto de proyección a 590 km (la distancia a la que está la órbita del telescopio Hubble, aunque este no mira hacia la Tierra), a 35.786 km (altura a la que suelen estar los satélites) y a 378.000 km (más o menos la órbita de la Luna). Imagen de [6]
Mapas realizados con la proyección en perspectiva vertical, con imágenes reales del proyecto “The Blue Marble New Generation” de la NASA, con el centro de proyección sobre el Ecuador, cerca de la desembocadura del río Amazonas, y con el punto de proyección a 590 km (la distancia a la que está la órbita del telescopio Hubble, aunque este no mira hacia la Tierra), a 35.786 km (altura a la que suelen estar los satélites) y a 378.000 km (más o menos la órbita de la Luna). Imagen de [6]
Pero estamos hablando de proyecciones matemáticas, y no de fotografía, por lo que podemos proyectar desde cualquier punto, incluso que esté en el interior del globo terrestre, y con el plano de proyección situado en cualquier posición, por ejemplo, en el lado opuesto, al punto de perspectiva, de la Tierra (lo que se llaman mapas en perspectiva vertical lejanos). Las proyecciones gnomónica, estereográfica y ortográfica (que veremos en el siguiente retrato) son casos particulares de la familia de proyecciones en perspectiva. Los siguientes diagramas nos muestran las diferentes opciones.
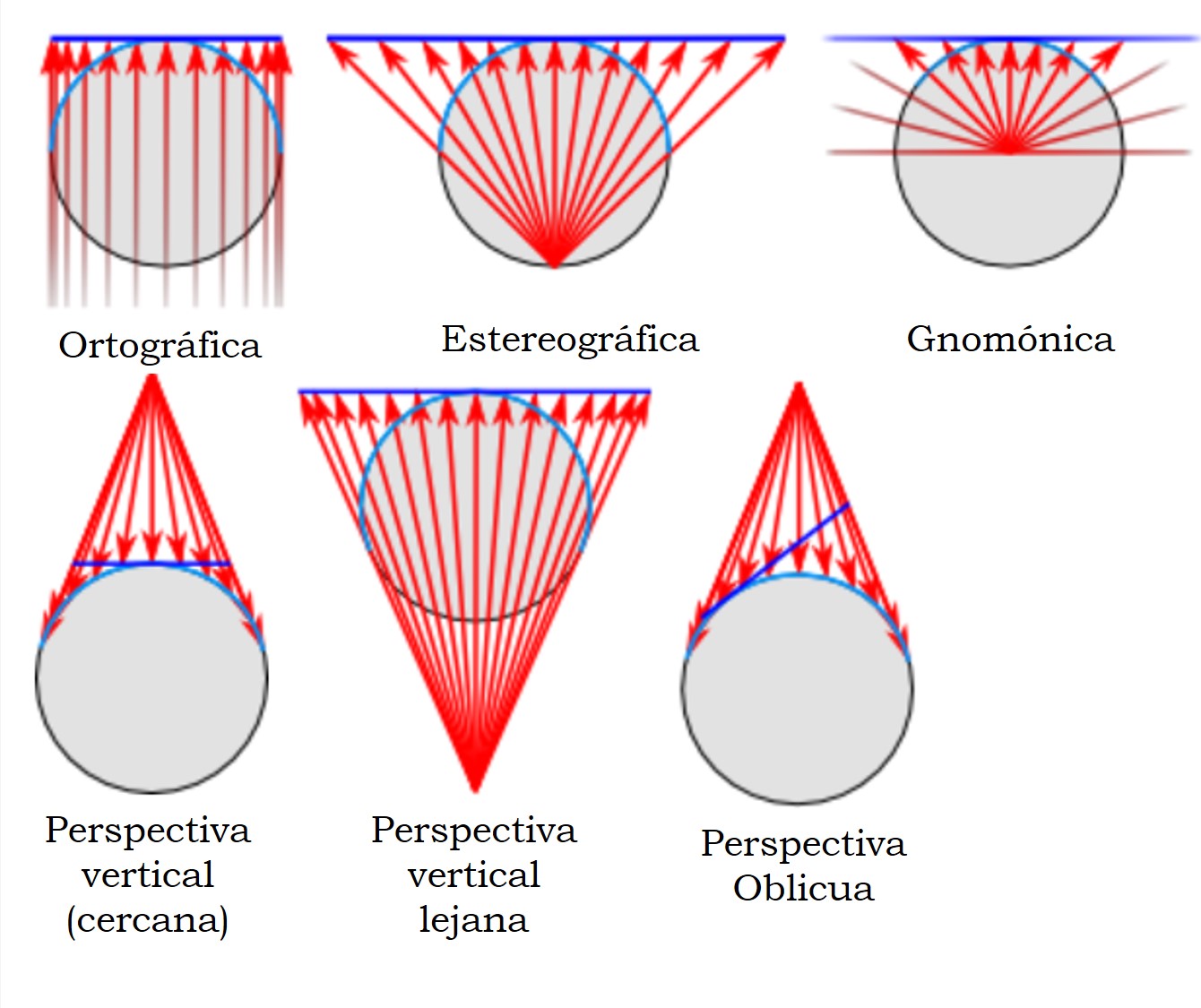 Diagramas de las diferentes proyecciones pertenecientes a la familia de proyecciones en perspectiva, dependiendo de la situación del punto de proyección y del plano sobre el que se proyecta. Imagen de [6]Para esta proyección, el meridiano y paralelo centrales se transforman en rectas, mientras que los demás meridianos y paralelos se transformarán en rectas, arcos de circunferencia o elipses, incluso en parábolas e hiperbolas, dependiendo del aspecto de la proyección (polar, ecuatorial u oblicua). No se preservan las propiedades métricas y existe una menor distorsión cerca del centro de proyección y una deformación exagerada en los bordes. Esta proyección, en su caso general, no fue prácticamente utilizada más que para representar la Tierra vista desde el espacio.
Diagramas de las diferentes proyecciones pertenecientes a la familia de proyecciones en perspectiva, dependiendo de la situación del punto de proyección y del plano sobre el que se proyecta. Imagen de [6]Para esta proyección, el meridiano y paralelo centrales se transforman en rectas, mientras que los demás meridianos y paralelos se transformarán en rectas, arcos de circunferencia o elipses, incluso en parábolas e hiperbolas, dependiendo del aspecto de la proyección (polar, ecuatorial u oblicua). No se preservan las propiedades métricas y existe una menor distorsión cerca del centro de proyección y una deformación exagerada en los bordes. Esta proyección, en su caso general, no fue prácticamente utilizada más que para representar la Tierra vista desde el espacio.
Mientras que las imágenes en perspectiva vertical general (con el plano cercano) nos muestran solo una parte de uno de los hemisferios, mediante el uso de un plano “lejano”, en la parte opuesta, de la superficie terrestre, al punto de proyección, se pueden obtener mapas que cubran más que un hemisferio.
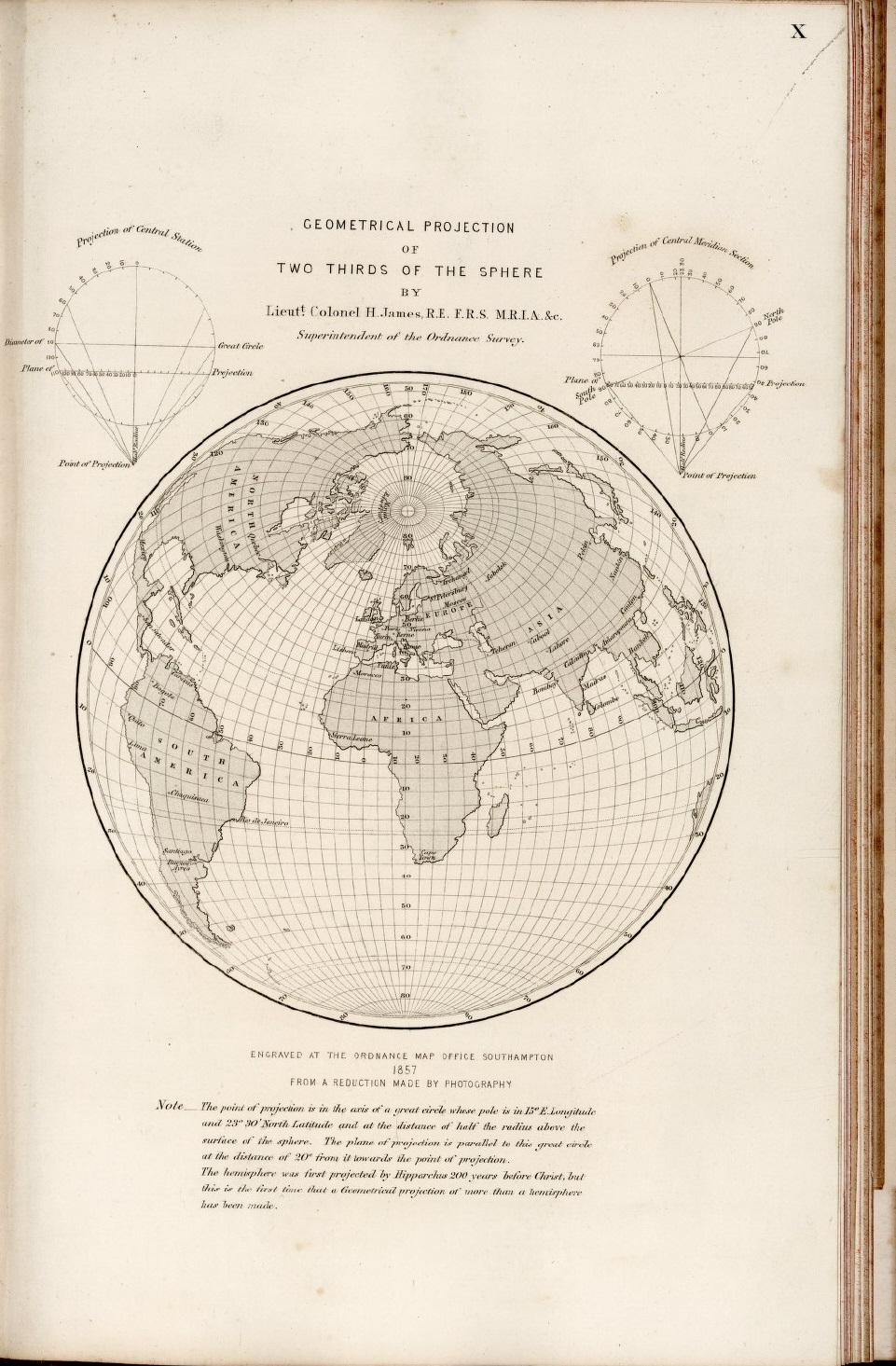 Mapa de dos tercios de la superficie terrestre, realizado en 1857 por el coronel Henry James, con la proyección en perspectiva vertical lejana, con una distancia de 1,5 veces el radio de la Tierra, desde el centro y en dirección opuesta al plano de proyección. Imagen de [1]
Mapa de dos tercios de la superficie terrestre, realizado en 1857 por el coronel Henry James, con la proyección en perspectiva vertical lejana, con una distancia de 1,5 veces el radio de la Tierra, desde el centro y en dirección opuesta al plano de proyección. Imagen de [1]
Por este motivo, la proyección en perspectiva vertical lejana fue utilizada por varios autores. El matemático francés Phillipe de La Hire (1640-1719) en 1701 con una distancia del punto de proyección de 1,7 veces el radio de la Tierra, desde el centro y en dirección opuesta al plano de proyección, el coronel británico Henry James (1803-1877), quien fuera director general de la agencia de mapas de Gran Bretaña, con una distancia de 1,5 veces el radio terrestre en 1857, el geodesta británico Alexander R. Clarke (1828-1914), junto con Henry James, a una distancia de 1,368 veces, en 1862, o solo, en su famosa “proyección crepúsculo”, con el plano a una distancia de 1,4 veces el radio de la Tierra, en 1879.
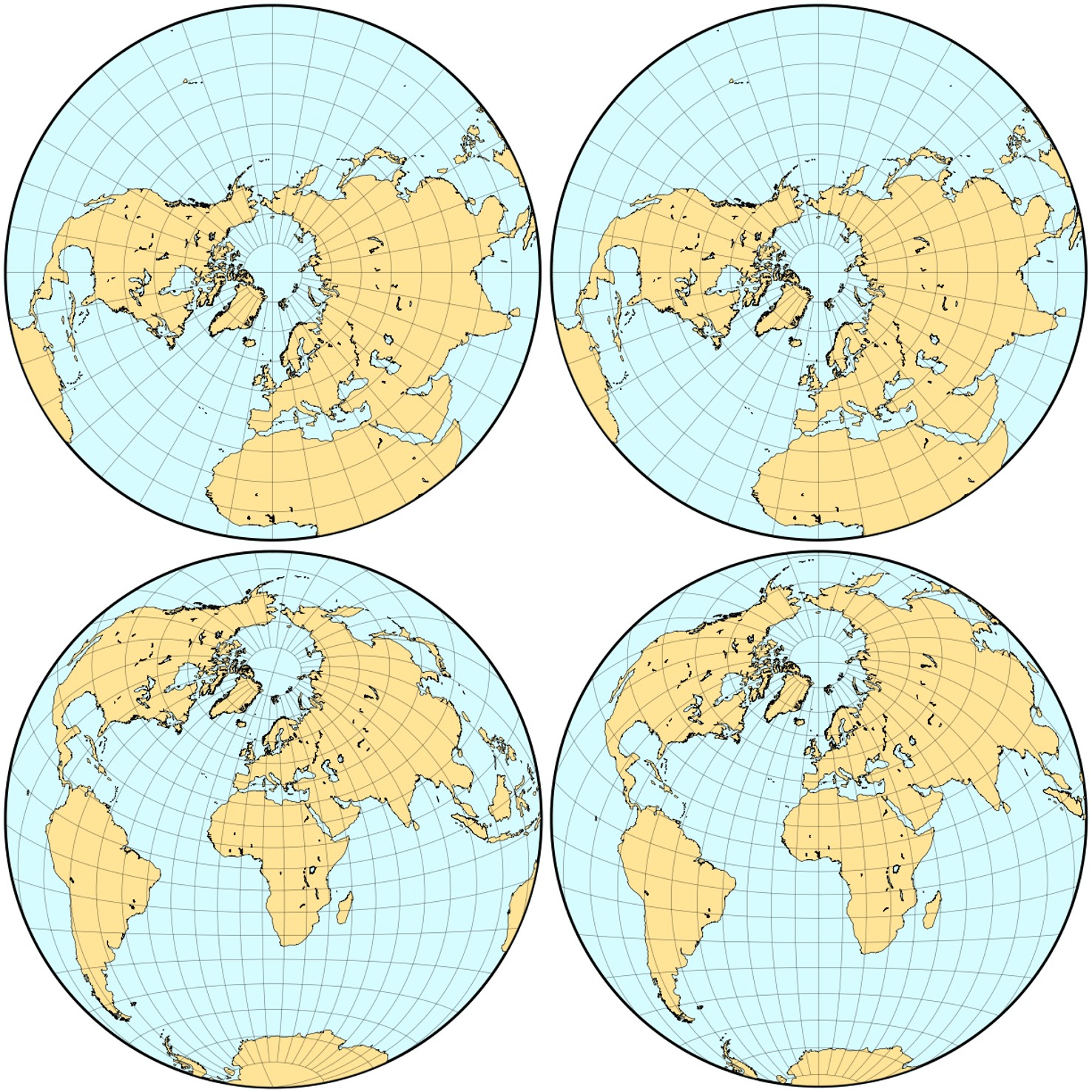 Reproducción de Carlos A. Furuti [6] de los mapas de Phillipe de La Hire (1701), Henry James (1857), Alexander R. Clarke (1862), junto con Henry James, o solo, en su famosa “proyección crepúsculo” (1879), realizados con proyecciones en perspectiva vertical lejana
Reproducción de Carlos A. Furuti [6] de los mapas de Phillipe de La Hire (1701), Henry James (1857), Alexander R. Clarke (1862), junto con Henry James, o solo, en su famosa “proyección crepúsculo” (1879), realizados con proyecciones en perspectiva vertical lejana
Retrato 2: La proyección ortográfica
La proyección en perspectiva es un caso particular de la anterior familia, si consideramos que el punto de proyección está lejos, en el infinito, luego los rayos de proyección van paralelos entre sí y perpendiculares al plano de proyección.
 Mapa del mundo, de la zona del Atlático, realizado con la proyección ortográfica, publicado por Richard E. Harrison como suplemento de la revista Fortune, en junio de 1942, el primero de una serie de tres mapas ortográficos. Imagen de [1]
Mapa del mundo, de la zona del Atlático, realizado con la proyección ortográfica, publicado por Richard E. Harrison como suplemento de la revista Fortune, en junio de 1942, el primero de una serie de tres mapas ortográficos. Imagen de [1]
Esta proyección ya era conocida desde la antigüedad. Seguramente la era conocida por los egipcios y el matemático y astrónomo Hiparco de Nicea (aprox. 190-120 a.n.e.) la utilizó para sus cálculos de astronomía. En la antigüedad se conocía con el nombre de “analema”, que sería reemplazado por “ortográfica” en 1613, por el matemático francés Francois d’Aguillon (1567-1617). Aunque fue utilizada por primera vez para mapas del mundo en el siglo XVI, por el cartógrafo austriaco Johannes Stabius (1450-1522) y el artista renacentista alemán Alberto Durero (1471-1528).
 Grabado coloreado de Alberto Durero de un mapa de Johannes Stabius, de 1515. Imagen de Media Storehouse
Grabado coloreado de Alberto Durero de un mapa de Johannes Stabius, de 1515. Imagen de Media Storehouse
Esta proyección se suele utilizar por su aspecto similar al aspecto que tiene el planeta visto desde el espacio. No es una proyección que se haya utilizado en muchos atlas, pero sí en algunos, cuando se quiere mostrar la imagen de la Tierra desde el espacio exterior, como en The Global Atlas, A New View of the World from Space, publicado por Frank Debenham en 1958, en varios de los atlas de Rand McNally o por la US Geological Survey, USGS. Y volvió a utilizarse cuando empezó la carrera espacial.
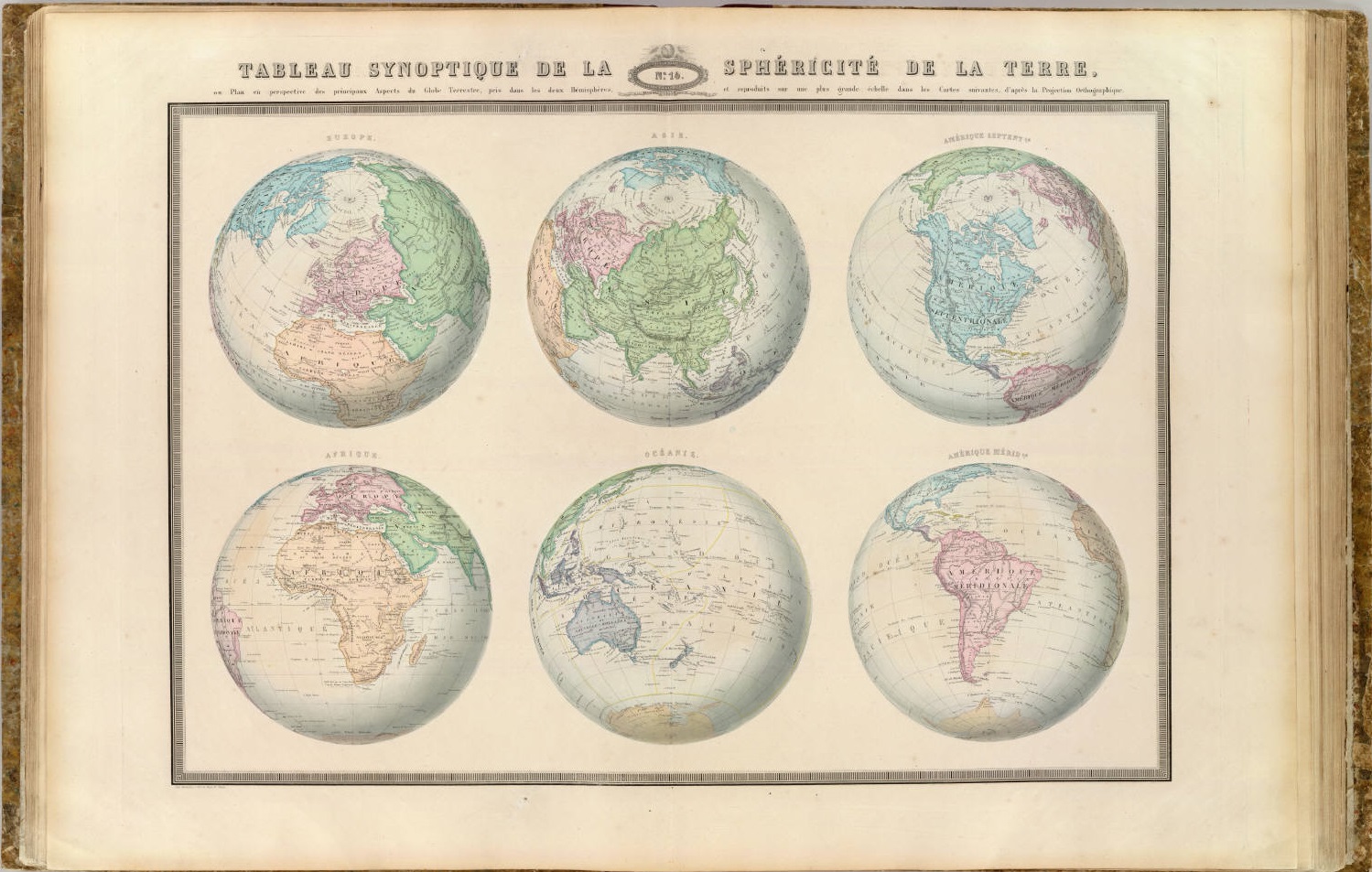 “Tabla sinóptica de la esfericidad de la Tierra”, con seis mapas hemisféricos, realizados con la proyección ortogonal, de la Tierra: Europa, Asia, Norteamérica, África, Oceanía y América del Sur, perteneciente a la publicación de M.F.A. Garnier, Atlas spheroidal et universel de geographie dresse a l’aide des documents officiels, recemment publies en France et a l’etranger (1862). Imagen de [1]
“Tabla sinóptica de la esfericidad de la Tierra”, con seis mapas hemisféricos, realizados con la proyección ortogonal, de la Tierra: Europa, Asia, Norteamérica, África, Oceanía y América del Sur, perteneciente a la publicación de M.F.A. Garnier, Atlas spheroidal et universel de geographie dresse a l’aide des documents officiels, recemment publies en France et a l’etranger (1862). Imagen de [1]
Retrato 3: La proyección cónica conforme de Lambert
Tanto en las dos primeras entregas de esta serie de retratos del mundo, Imagi Mundi, como en los dos primeros retratos de esta tercera entrega, solamente hemos presentado proyecciones cilíndricas y acimutales, o generalizaciones de estas. Ahora vamos a presentar algunas proyecciones cónicas, es decir, cuya superficie auxiliar de proyección es el cono. Es decir, en el caso de las proyecciones geométricas, se proyecta primero la esfera terrestre básica sobre un cono, tangente (la intersección es una circunferencia, que será un paralelo en el caso normal, esto es, si el eje del cono coincide con el de la esfera terrestre básica) o secante (con dos circunferencias de intersección, que serán paralelos en el caso normal), a la esfera y luego este se despliega, cortando por una de sus rectas generadoras, en un plano.
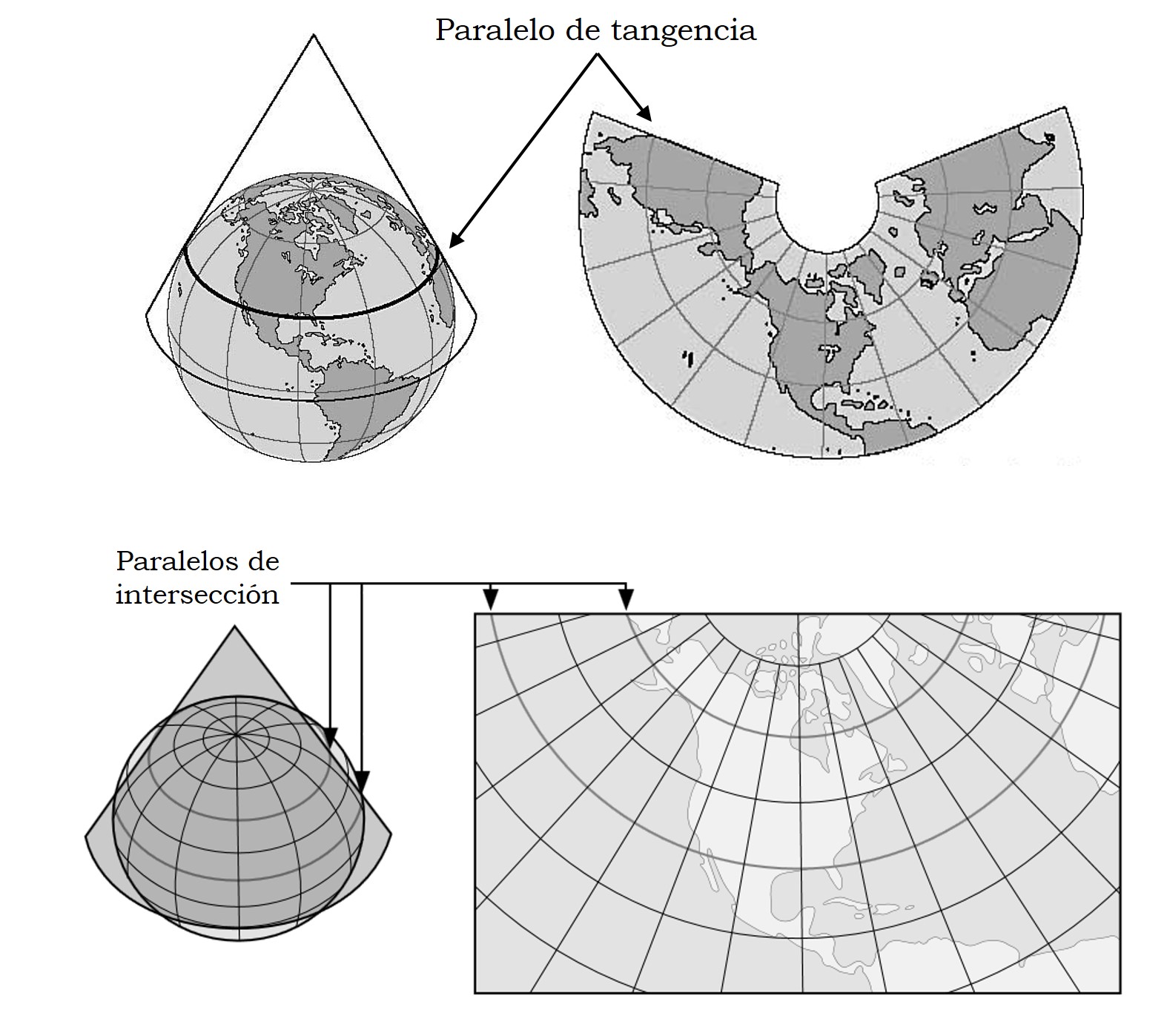 Esquemas de las proyecciones cónicas en el caso normal (el eje del cono y la esfera es el mismo), tangentes (con un paralelo de tangencia) y secantes (con dos paralelos de intersección)
Esquemas de las proyecciones cónicas en el caso normal (el eje del cono y la esfera es el mismo), tangentes (con un paralelo de tangencia) y secantes (con dos paralelos de intersección)La proyección cónica conforme de Lambert es una de las siete proyecciones presentadas por el matemático alemán, aunque de origen francés, Johann H. Lambert (1728-1777) en su trabajo Notas y comentarios sobre la composición de mapas terrestres y celestes (1772). Lambert utilizó las herramientas matemáticas en su poder (cálculo, geometría, álgebra y trigonometría) para construir una familia de proyecciones conformes intermedias entre la proyección estereográfica (que es acimutal) y la proyección de Mercator (que es cilíndrica), para los casos tangentes (con un paralelo de tangencia) y secantes (con dos paralelos de intersección).
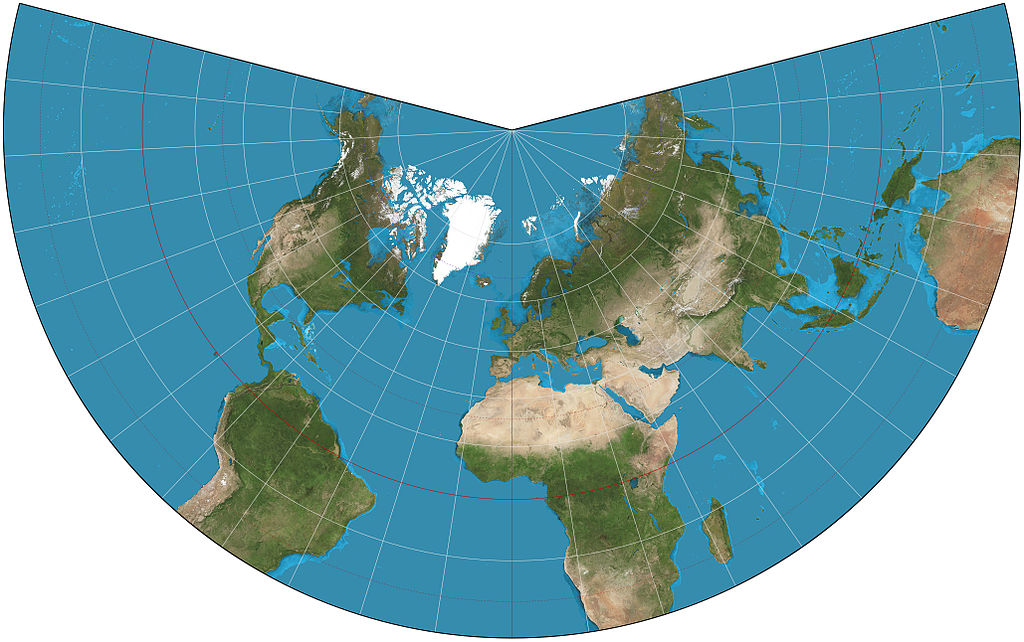 Mapa del mundo realizado con la proyección cónica conforme de Lambert, cuyos paralelos de tangencia a 20º N y 50º N, con imágenes del proyecto “Blue Marble” de la NASA. Imagen de Wikimedia Commons
Mapa del mundo realizado con la proyección cónica conforme de Lambert, cuyos paralelos de tangencia a 20º N y 50º N, con imágenes del proyecto “Blue Marble” de la NASA. Imagen de Wikimedia Commons
Como hemos comentado, esta proyección es conforme, preserva los ángulos, los rumbos, y para regiones pequeñas también las formas. La deformación es pequeña cerca de los paralelos de tangencia o intersección, y mayor al alejarse de ellos. Por este motivo, la proyección es muy útil para mapas de territorios en la dirección este-oeste, que se desarrollen alrededor del paralelo de tangencia o entre los dos paralelos de intersección, no estando estos muy alejados.
Hasta que fue utilizada por Francia durante la primera guerra mundial, esta proyección había permanecido olvidada. Después se ha convertido en una de las proyecciones más utilizadas para mapas de “escala grande” (esto es, es factor de proporcionalidad de la escala es pequeño), es decir, mapas de territorios pequeños. La utiliza la USGS de Estados Unidos, así como muchas otras agencias internacionales, para mapas topográficos. La Comisión Europea la recomienda para mapas conformes de Europa al completo de escalas mayores o iguales a 1:500.000 (como 1:100.000 o 1:25.000), y es común en países como Francia, Estados Unidos, Canada o México. También se emplea mucho para cartas náuticas.
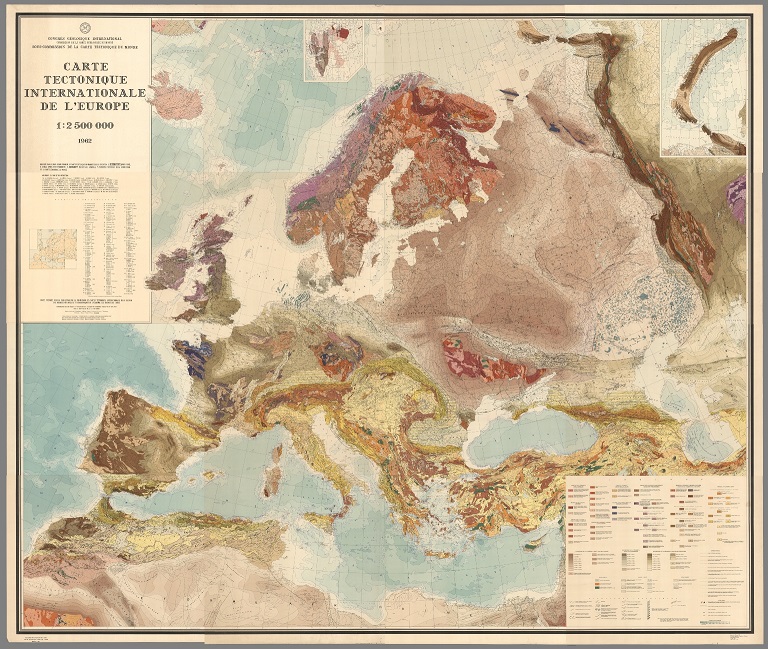 “Carta tectónica internacional de Europa”, realizada con la proyección cónica conforme de Lambert, por el Congreso Internacional de Geología, Academia de Ciencias de la URSS, 1962. Imagen de [1]
“Carta tectónica internacional de Europa”, realizada con la proyección cónica conforme de Lambert, por el Congreso Internacional de Geología, Academia de Ciencias de la URSS, 1962. Imagen de [1]
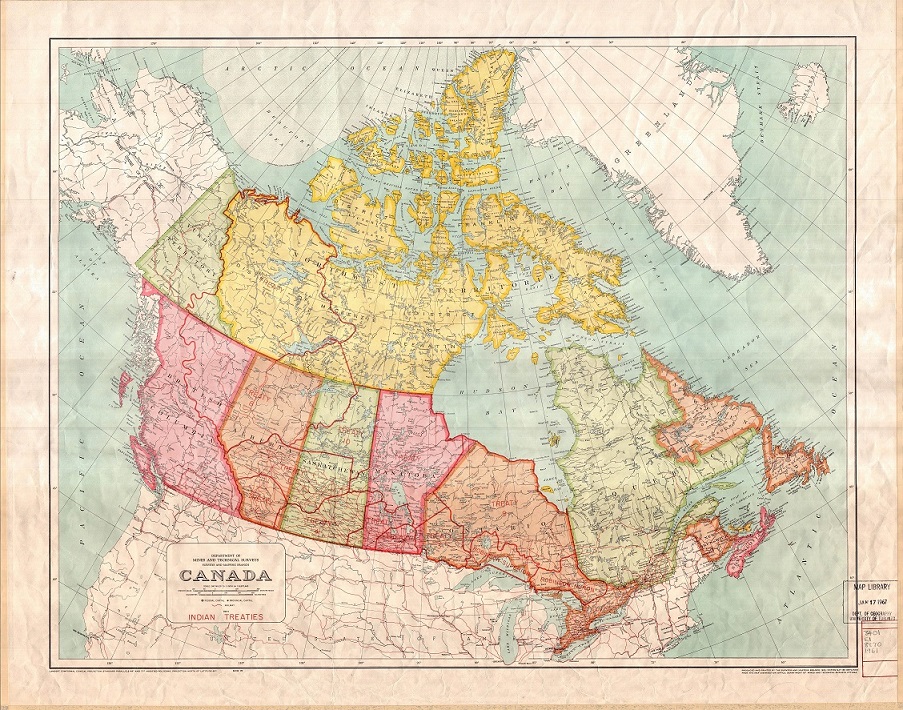 “Mapa de tratados indios de Canada”, realizado con la proyección cónica conforme de Lambert, del “Department of Mines and Technical Surveys” de Canada, 1961. Imagen de University of Toronto Libraries
“Mapa de tratados indios de Canada”, realizado con la proyección cónica conforme de Lambert, del “Department of Mines and Technical Surveys” de Canada, 1961. Imagen de University of Toronto Libraries
Retrato 4: La proyección cónica isoareal de Albers
En su monografía de 1772, Johann Lambert también propuso una proyección cónica isoareal, que sería generalizada por el cartógrafo alemán Heinrich C. Albers (1773-1833) en 1805, también con uno o dos paralelos de intersección, que son aquellos en los que la escala es real (luego son llamados paralelos estándar). Como en el caso de la proyección cónica conforme de Lambert, los paralelos son arcos de circunferencias concéntricas y los meridianos son radios –rectas- de esas circunferencias igualmente espaciados, que cortan perpendicularmente a los paralelos. Los polos son arcos de circunferencia, el interior y el exterior, mientras que en la cónica conforme de Lambert era un punto (el norte o el sur, dependiendo de la versión), y el infinito.
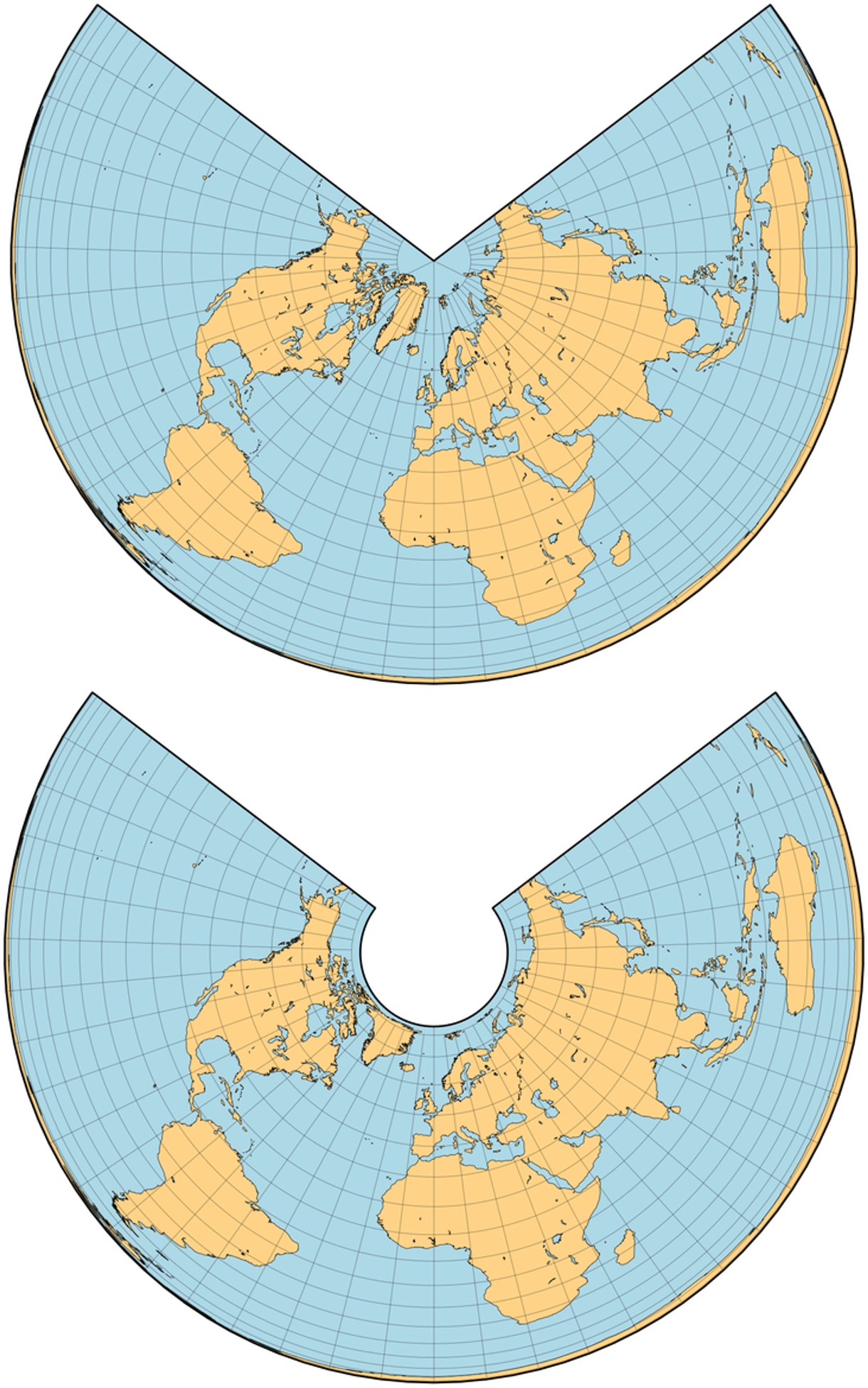 Mapas del mundo realizados con las proyecciones cónica isoareales de Lambert (con paralelos estándar a 90ºN y 24º 28’ 11’’N) y Albers (con paralelo estándar a 45ºN). Imagen de [6]
Mapas del mundo realizados con las proyecciones cónica isoareales de Lambert (con paralelos estándar a 90ºN y 24º 28’ 11’’N) y Albers (con paralelo estándar a 45ºN). Imagen de [6]
De nuevo, la deformación es pequeña cerca de los paralelos de tangencia o intersección, y mayor al alejarse de ellos, por lo que también es útil para mapas este-oeste. En particular, es una proyección, con deos paralelos estándar, muy utilizada para los mapas de Estados Unidos.
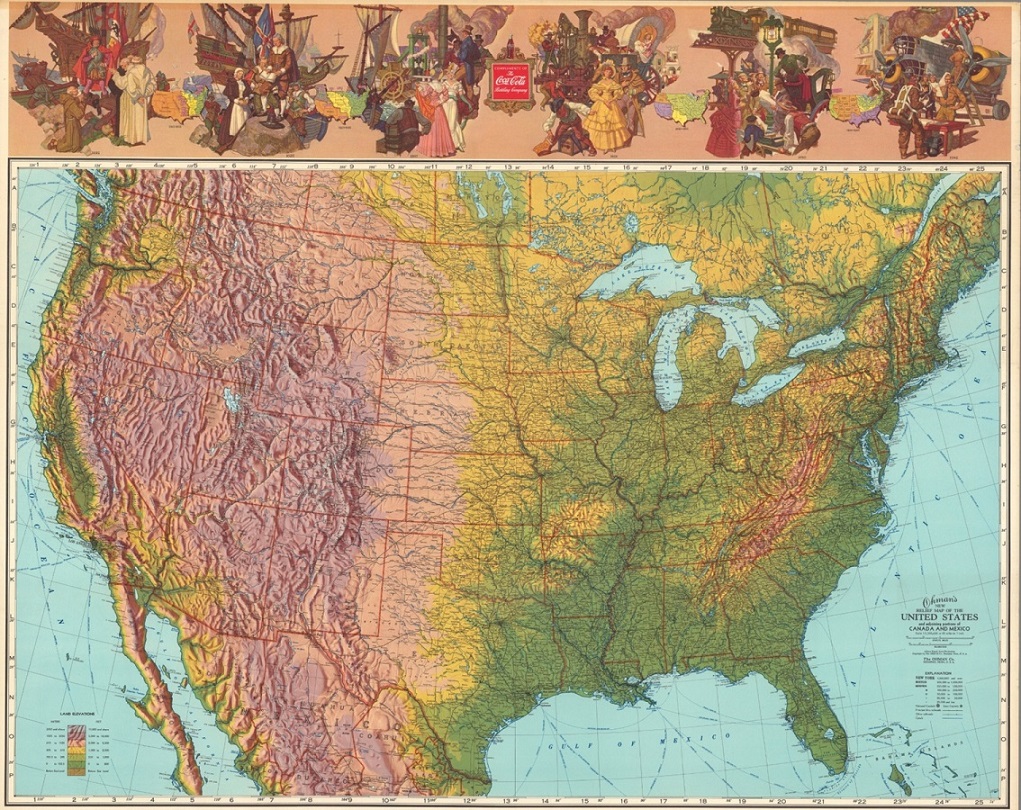 Mapa en relieve de Estados Unidos, realizado con la proyección cónica isoareal de Albers, publicado por la Ohman Company en 1942. Imagen de [1]
Mapa en relieve de Estados Unidos, realizado con la proyección cónica isoareal de Albers, publicado por la Ohman Company en 1942. Imagen de [1]
Retrato 5: La proyección de Bonne
En las proyecciones cónicas, ya sean geometricas puras o su generalización matemática, los meridianos (en la versión normal) se representan como radios (rectas), igualmente espaciados, de los arcos de circunferencias concéntricas que representan a los paralelos, mientras que en la generalización de estas proyecciones, las llamadas pseudo-cónicas, los meridianos siguen siendo arcos de circunferencia, mientras que los paralelos ya no son rectas.
Un ejemplo de proyección pseudo-cónica es la proyección de Bonne, que realmente es toda una familia de proyecciones pseudo-cónicas isoareales, en función de cual sea el paralelo estándar o central (correspondiente al paralelo de intersección con el cono).
 Mapamundis realizados con la proyección de Bonne, para los paralelos estándar de 45ºN, en el primero, y 15ºS, en el segundo
Mapamundis realizados con la proyección de Bonne, para los paralelos estándar de 45ºN, en el primero, y 15ºS, en el segundo
El autor de esta familia de proyecciones fue el cartógrafo e ingeniero francés Rigobert Bonne (1727-1795). Aunque la proyección de Bonne ya había sido utilizada con anterioridad. Por ejemplo, en el mapa Universalis Cosmographia del cartógrafo alemán Martin Waldseemüller (1470-1520) de 1507 que modifica la segunda proyección de Ptolomeo o en su generalización en el mapa del mundo de Petrus Apianus de 1520, así como en el mapa del mundo del cartógrafo italiano Bernardo Sylvanus de 1511.
 Mapa “Universalis Cosmographia” de Martin Waldseemüller (1507), en el que aparece, por primera vez en un mapa, la palabra “América”
Mapa “Universalis Cosmographia” de Martin Waldseemüller (1507), en el que aparece, por primera vez en un mapa, la palabra “América” Planisferio de Sylvanus (1511)
Planisferio de Sylvanus (1511)Los casos extremos son la proyección de Werner (o Stabius-Werner), cuando el paralelo estandar es 90ºN, que tiene forma de corazón y la proyección sinusoidal o de Sanson-Flamsteed, cuando el paralelo es 0º.
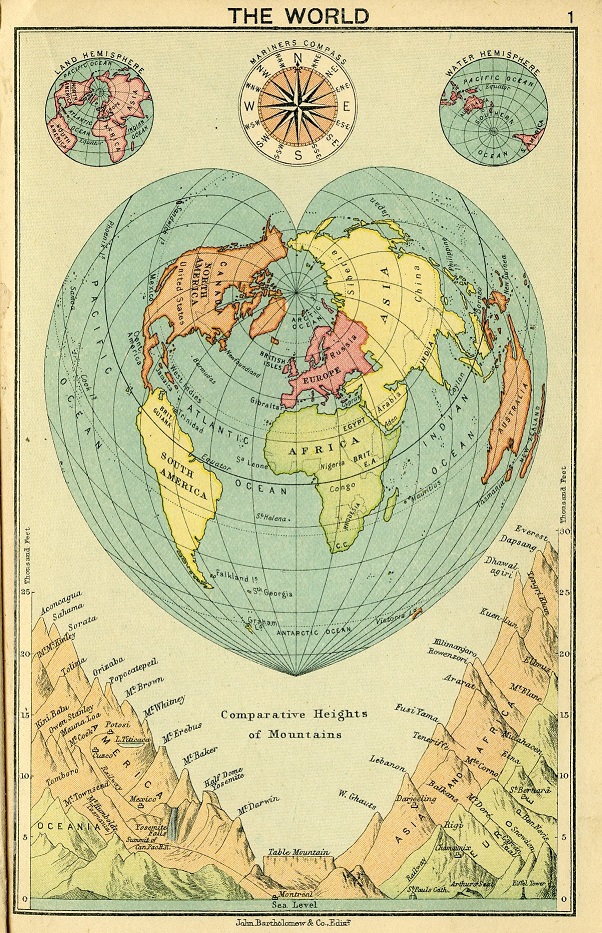 Mapa del mundo, realizado con la proyección de (Stabius-) Werner, perteneciente al “Atlas del mundo” (1913), de John Bartholomew. Imagen de University of Toronto Libraries
Mapa del mundo, realizado con la proyección de (Stabius-) Werner, perteneciente al “Atlas del mundo” (1913), de John Bartholomew. Imagen de University of Toronto Libraries
La proyección sinusoidal tiene este nombre ya que los meridianos son sinusoides, curvas de la función seno, mientras que los paralelos son rectas estándar, es decir, la escala es correcta a lo largo de los paralelos. Por este motivo, el mapa diseñado con la proyección sinusoidal se va encogiendo según los paralelos van acercándose a los polos, que son dos puntos. Para que la compresión no sea tan fuerte en los polos, se suele utilizar una versión cortada, o interrumpida.
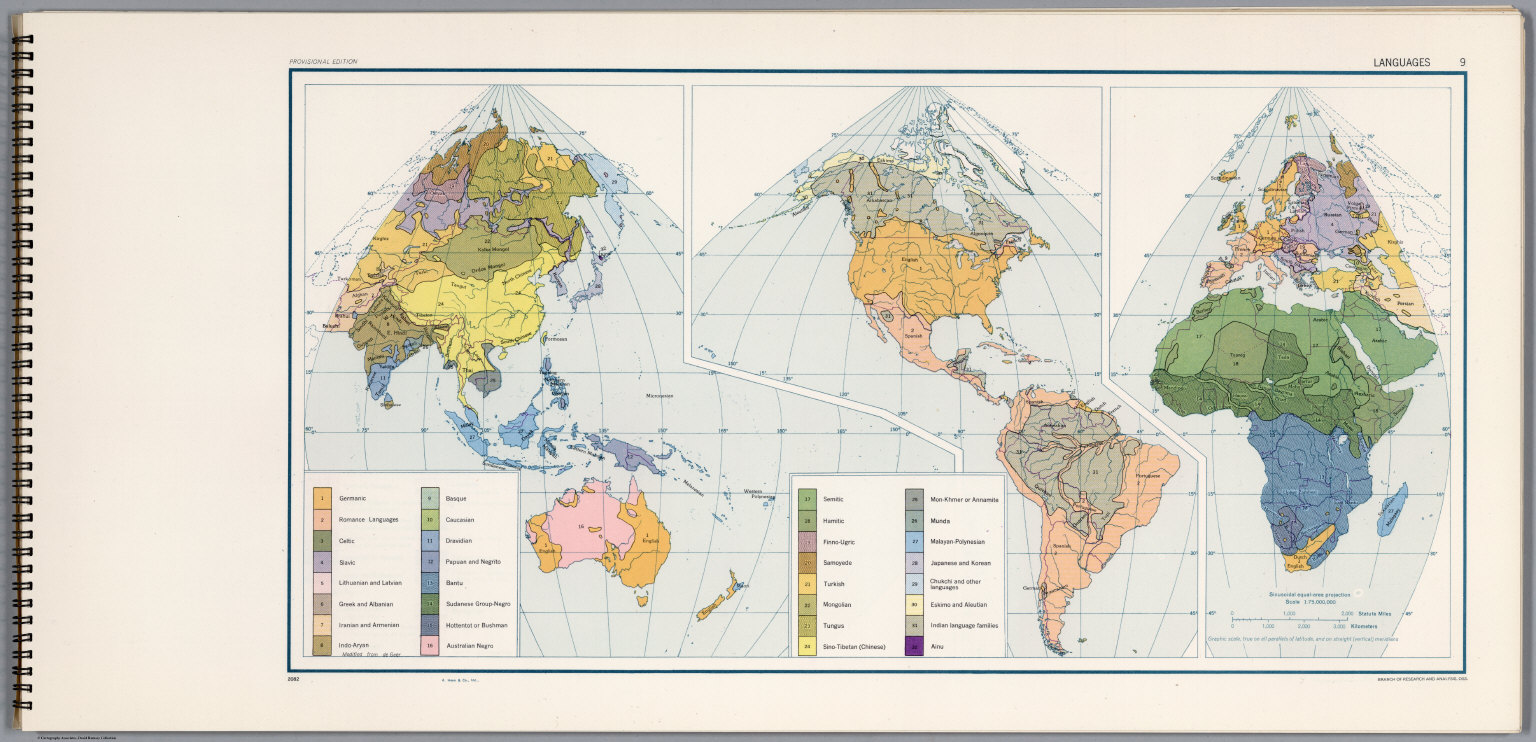 Mapa con las lenguas del mundo, realizado con la proyección sinusoidal interrumpida, perteneciente al “Atlas del mundo para el estudio de la Geografía en el Programa de Entrenamiento Especial del Ejército”, United States Army Service Forces, 1943. Aparecen el euskera (zona del País Vasco y Navarra) y el catalán (aunque solo señalado en las Islas Baleares). Imagen de [1]
Mapa con las lenguas del mundo, realizado con la proyección sinusoidal interrumpida, perteneciente al “Atlas del mundo para el estudio de la Geografía en el Programa de Entrenamiento Especial del Ejército”, United States Army Service Forces, 1943. Aparecen el euskera (zona del País Vasco y Navarra) y el catalán (aunque solo señalado en las Islas Baleares). Imagen de [1]
Retrato 7: La proyección armadillo
Como ya hemos comentado, existen tres familias principales de proyecciones, en función de si la superficie auxiliar de proyección no existe (acimulates), es un cilindro (cilíndricas) o es un cono (cónicas). También se podrían tomar otras superficies auxiliares intermedias no necesariamente desarrollables, aunque no suele ser lo habitual, como en la proyección armadillo, desarrollada en 1943 por el cartógrafo estadounidense, de origen húngaro, Erwin J. Raisz (1893-1968), que consiste en proyectar la superficie terrestre básica sobre un toro (recordemos que en las matemáticas un “toro” es la superficie que tiene la forma de un flotador) y luego proyectar ortogonalmente, según una cierta dirección, en un plano.
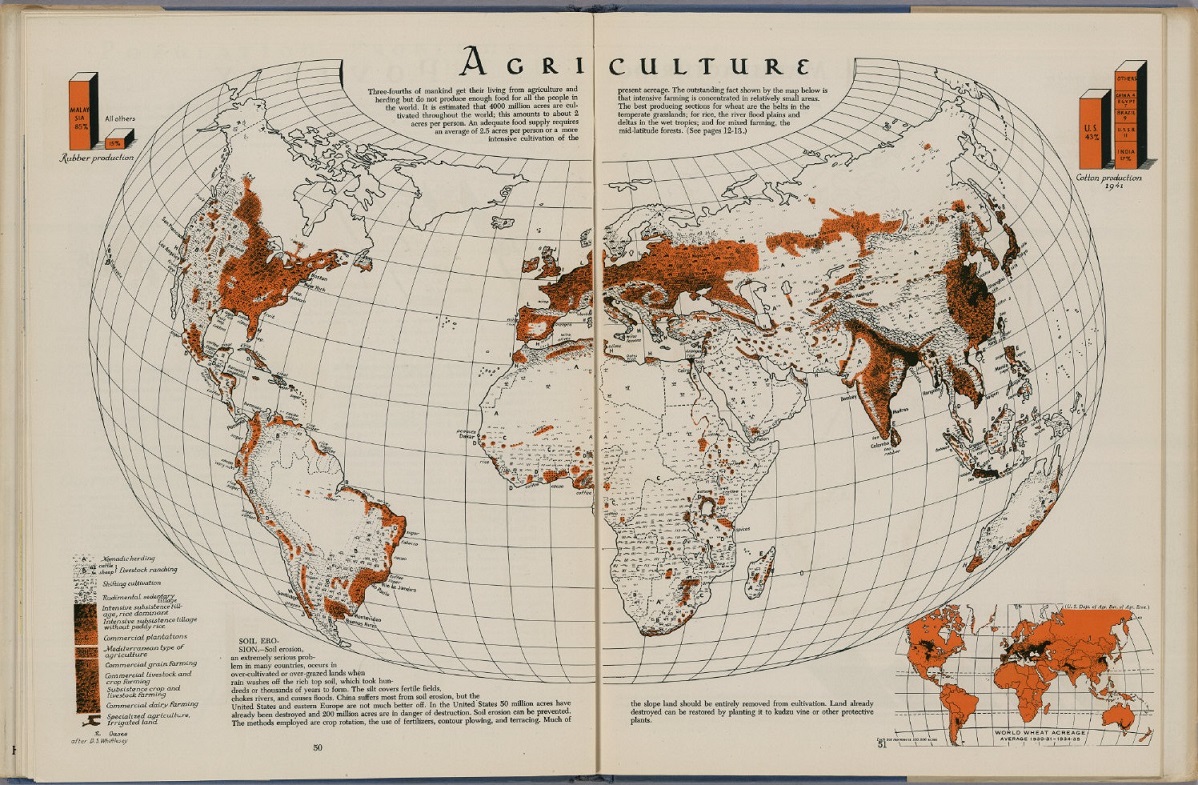 Mapa del mundo sobre agricultura, realizado con la proyección armadillo, perteneciente al “Atlas de geografía global” (1944), de Edwin Raisz. Imagen de [1]
Mapa del mundo sobre agricultura, realizado con la proyección armadillo, perteneciente al “Atlas de geografía global” (1944), de Edwin Raisz. Imagen de [1]
Retrato 8: La proyección globular de Nicolosi
Las proyecciones globulares son aquellas que pretenden representar la imagen esférica del globo terrestre, y contrariamente a las proyecciones acimutales, no son proyecciones geométricas, es decir, no están definidas a través de “rayos”, como ocurre en proyecciones acimutales como la gnomónica o la estereográfica, y en proyecciones cilíndricas como la proyección cilíndrica isoareal de Lambert. No preservan ni áreas, ni ángulos. Se limitan a un hemisferio, por lo que se necesitan dos mapas para cubrir toda la superficie terrestre.
Son proyecciones muy antiguas. Una de las proyecciones globulares más antiguas fue descrita por el filósofo inglés Roger Bacon (1214-1294) hacia 1265. La proyección globular conocida como de “Nicolosi”, que es una modificación de una proyección globular, la llamada primera, del jesuita, geógrafo y matemático francés Georges Fournier (1595-1652), fue realizada por el geógrafo italiano Giovanni Battista Nicolosi (1610-1670), aunque seguramente fue creada por el matemático persa Al-Biruni (973-1048).
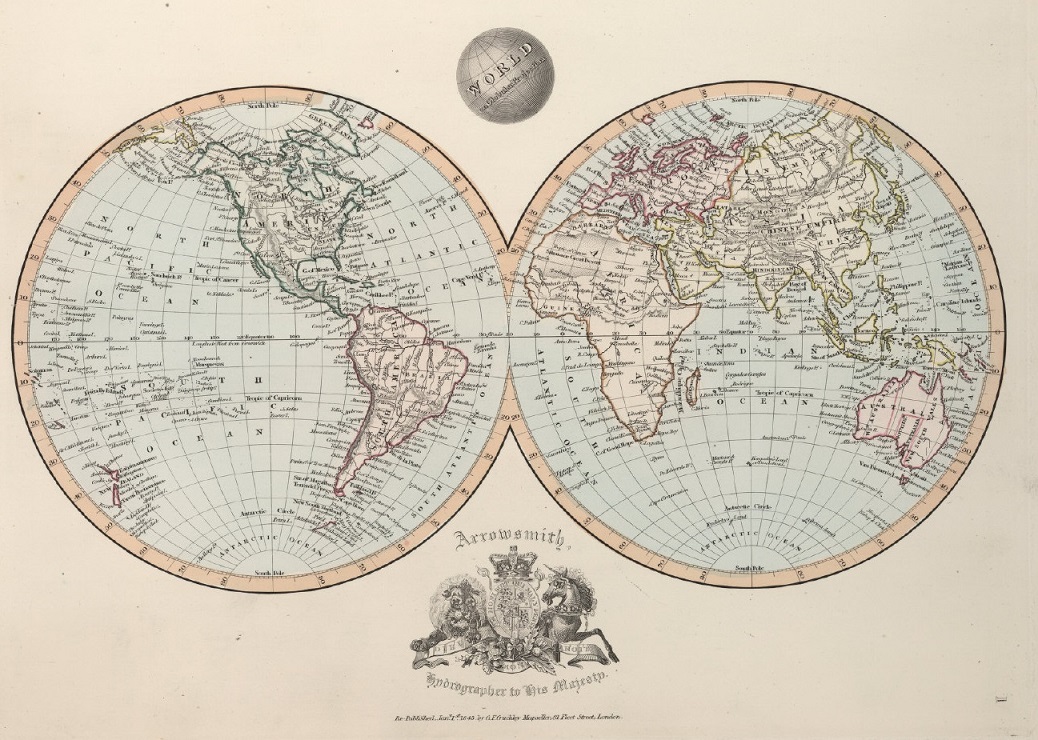 “El mundo en la proyección globular” (de Nicolosi), de la publicación Outlines of the World (1845), de Aaron Jr. Arrowsmith. Imagen de [1]
“El mundo en la proyección globular” (de Nicolosi), de la publicación Outlines of the World (1845), de Aaron Jr. Arrowsmith. Imagen de [1]
En el mapamundi diseñado con la proyección globular de Nicolosi los meridianos y paralelos son circulares. De las proyecciones globulares, esta es la que produce menos distorsión en las formas. En la mayoría de los mapas modernos en los cuales se menciona que han sido diseñados con la proyección globular, se están refiriendo a la proyección globular de Nisolosi.
Retrato 9: La proyección regional de Bartholomew
En 1958 el cartógrafo escocés John C. Bartholomew (1923-2008) combinó la proyección cónica equidistante (esta una proyección cónica sencilla, donde los meridianos son rectas estándar, es decir, la escala es correcta a lo largo de los meridianos, igualmente espaciadas y los paralelos son arcos de circunferencia, igualmente espaciados, además, los dos paralelos de intersección con el cono son también curvas estándar), para latitudes por encima del Trópico de Cáncer (22,5ºN), y la proyección de Bonne interrumpida para el resto de la superficie terrestre.
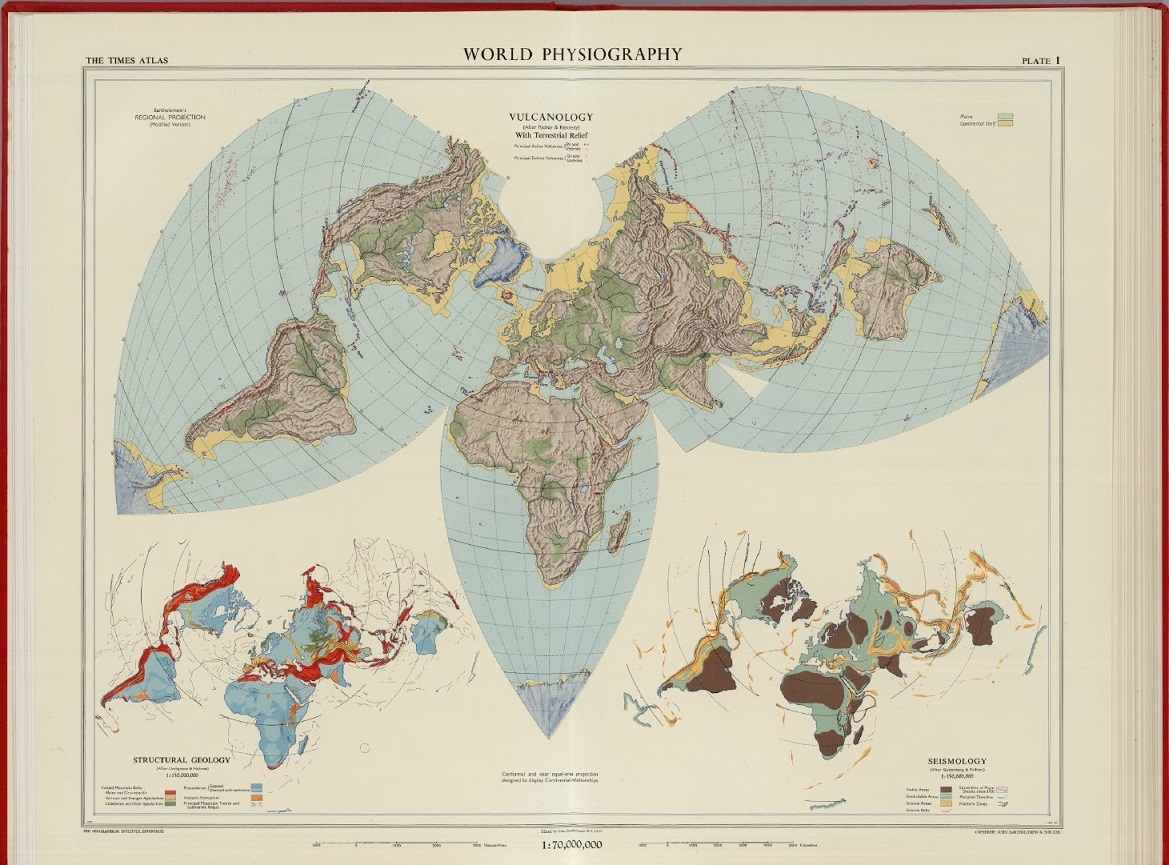 Mapa “Fisiografía del mundo”, realizado con la proyección regional de Bartholomew, perteneciente a la publicación “The Times Atlas of the World” (1958), de John C. Bartholomew (editor), Houghton Mifflin. Imagen de [1]
Mapa “Fisiografía del mundo”, realizado con la proyección regional de Bartholomew, perteneciente a la publicación “The Times Atlas of the World” (1958), de John C. Bartholomew (editor), Houghton Mifflin. Imagen de [1]
Existen muchas más projecciones cartográficas, pero parafraseando al matemático británico Andrew Wiles, “creo que lo dejaré aquí”.
 “Going Global”, de la serie “American History” (2004), de la artista estadounidense Joyce Kozloff, cuya obra artística está basada en la cartografía. Esta obra contiene un mapamundo realizado con la proyección homolosena de Goode. Imagen de [8]
“Going Global”, de la serie “American History” (2004), de la artista estadounidense Joyce Kozloff, cuya obra artística está basada en la cartografía. Esta obra contiene un mapamundo realizado con la proyección homolosena de Goode. Imagen de [8]
Bibliografía
1.- David Rumsey Map Collection
2.- National Geographic, Maps
3.- Raúl Ibáñez, El sueño del mapa perfecto; cartografía y matemáticas, RBA, 2010.
4.- Raúl Ibáñez, Muerte de un cartógrafo, Un paseo por la Geometría, UPV/EHU, 2002. Versión online en la sección textos-on-line de divulgamat
5.- J. P. Snyder, Flattening the Earth, Two Thousand Years of Map Projections, The University of Chicago Press, 1993.
6.- Carlos Furuti, Map projections
7.- J. P. Snyder, Map projections, A Working Manual, USGS Professional Paper 1395, 1987.
8.- Página web de la artista Joyce Kozloff
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo ‘Imago mundi’, finalmente 9 retratos más del mundo se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Cristalografía (13): Fiat Pasteur

Cuando el joven doctor Louis Pasteur, a la sazón profesor del instituto de secundaria de Dijon, se enfrentó a su primer proyecto de investigación en solitario pensó que lo primero que necesitaba era una profunda preparación en cristalografía práctica. Decidió que lo mejor que podía hacer era estudiar sistemáticamente las formas cristalinas, repetir todas las mediciones y comparar sus resultados con los publicados. Uno de los estudios cristalográficos que decidió repetir fue el de 1841 de Frédéric Hervé de la Provostaye.
Pasteur fue muy meticuloso en la repetición de los experimentos. Esta meticulosidad tuvo su premio en el descubrimiento de algo que aparentemente había escapado tanto al ojo de Mitscherlich como al del propio de la Provostaye: aparecían caras hemiédricas en los cristales de tartrato de sodio y amonio. Sin embargo los cristales del racemato también tenían caras hemiédricas; la muestra bruta estaba formada en realidad por una mezcla de caras hemiédricas izquierdas y derechas.
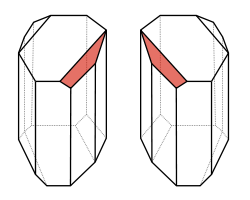
Pasteur, en vez de anotar el dato y seguir con otra cosa, decidió investigar un poco. Con ayuda de una lupa y unas pinzas separó los cristales diestros y los zurdos, y preparó disoluciones con ellos. Para su sorpresa la disolución de zurdos era levorrotatoria y la de los diestros dextrorrotatoria. Si disolvía cantidades iguales de zurdos y diestros la disolución resultante era ¡ópticamente inactiva!
A continuación Pasteur decidió que tenía que comprobar la composición química de los cristales zurdos y diestros. Para ello obtuvo los ácidos libres a partir de las sales: el diestro era idéntico en todo al tartárico, el zurdo era en todo el tartárico pero con actividad óptica inversa.
Con todos estos datos el investigador de 25 años llegó a las siguientes conclusiones:
a) El ácido racémico no es un compuesto puro, sino una mezcla de iguales cantidades de ácido tartárico zurdo y diestro, que se diferencian tan sólo en su actividad óptica. La rotación óptica de los dos compuestos se cancela y, por lo tanto, la mezcla es inactiva.
b) La actividad óptica de los compuestos orgánicos, sus disoluciones, y los líquidos es el resultado de la falta de simetría (Pasteur usaba la palabra disimetría) de las moléculas.
c) La actividad óptica de los cristales cuyas disoluciones (o fundidos) son ópticamente inactivos como, por ejemplo, el cuarzo o el clorato de sodio, se debe al empaquetamiento disimétrico de moléculas simétricas.
d) Al igual que sus cristales, las moléculas diestra y zurda del ácido tartárico eran imágenes especulares (enantiómeros).

Pasteur era muy consciente de la trascendencia de su descubrimiento y de su insignificancia dentro de la comunidad científica francesa. Por ello la forma en que decidiese comunicar sus resultados era de la mayor importancia. Así que, en vez de intentar publicar directamente, escribió a la única persona capaz de entender su trabajo y con influencia suficiente para conseguir una publicación con repercusión: Jean-Baptiste Biot, a la sazón con 74 años, a punto de dejar su cátedra en la Facultad de Ciencias de París y miembro de más de 20 academias científicas europeas y americanas.
Biot reconoció la importancia del descubrimiento inmediatamente y se mostró dispuesto a comunicarlo a la Academia de Ciencias de París a la primera oportunidad. Pero, y en esto Biot demostró ser un científico cabal, no antes de que se reprodujese el experimento en su laboratorio, ensayo al que invitó a asistir a Pasteur.
Biot proporcionó a Pasteur muestras de ácido racémico, preparada por él mismo y en la que había comprobado la inactividad óptica, hidróxido sódico y amoniaco y le pidió que preparase, a partir de ellas, en su presencia, la sal doble de sodio y amonio. Una vez preparada, Pasteur abandonó el edificio y la disolución se dejó evaporar en el laboratorio de Biot en el Collège de France. Cuando se habían separado algo más de 30 g de cristales, Biot convocó de nuevo a Pasteur para que separase los cristales en su presencia. Biot en persona preparó las disoluciones para comprobar la actividad óptica de los mismos. En cuanto colocó en el polarímetro la disolución que debía ser levógira y acercó su ojo al visor, Biot exclamó tomando la mano de Pasteur:
¡Mi querido hijo, he amado tanto durante toda mi vida esta ciencia que siento mi corazón latir de júbilo!
La comunicación a la Academia se produjo ese mismo año de 1848. En los años siguientes, ya profesor universitario en Estrasburgo, Pasteur continuó con sus estudios de la asimetría molecular y cristalina de muchos compuestos, incluyendo los aspartatos y malatos ópticamente activos y los inactivos que se comprobaba que eran “mezclas racémicas”.
En 1853, mismo año en el que se le haría caballero de la Orden Nacional de la Legión de Honor, Pasteur consiguió preparar el tercer isómero del ácido tartárico, ópticamente inactivo, hoy llamado meso-tartárico.
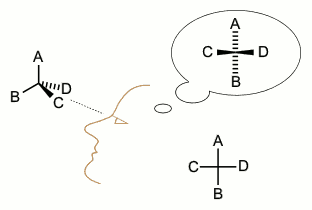
El descubrimiento de Pasteur de la quiralidad molecular (este nombre, ideado por Lord Kelvin en los años ochenta del XIX se acabaría imponiendo frente a las disimetrías de Pasteur) añadió la tercera dimensión a la química y fue el comienzo de la estereoquímica. En las décadas siguientes el concepto de molécula creció de una fórmula (1D), a un grafo (2D) y, finalmente, a finales del XIX, a un objeto 3D.
El modelo tetraédrico para los enlaces del carbono de van’t Hoff y le Bel (1874), el modelo octaédrico de coordinación de Werner (1893) y el trabajo monumental de Emil Fischer sobre la estereoquímica de los azúcares y las proyecciones moleculares (años noventa del XIX) toman como punto de partida el trabajo cristalográfico de Pasteur.
Referencias generales sobre historia de la cristalografía:
[1] Wikipedia (enlazada en el texto)
[3] Molčanov K. & Stilinović V. (2013). Chemical Crystallography before X-ray Diffraction., Angewandte Chemie (International ed. in English), PMID: 24065378
[4] Lalena J.N. (2006). From quartz to quasicrystals: probing nature’s geometric patterns in crystalline substances, Crystallography Reviews, 12 (2) 125-180. DOI:10.1080/08893110600838528
[5] Kubbinga H. (2012). Crystallography from Haüy to Laue: controversies on the molecular and atomistic nature of solids, Zeitschrift für Kristallographie, 227 (1) 1-26. DOI: 10.1524/zkri.2012.1459
[6] Schwarzenbach D. (2012). The success story of crystallography, Zeitschrift für Kristallographie, 227 (1) 52-62. DOI: 10.1524/zkri.2012.1453
Este texto es una revisión del publicado en Experientia docet el 6 de febrero de 2014
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Cristalografía (13): Fiat Pasteur se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Redes y arpones para cazar basura zombie en el espacio

El 4 de octubre de 1957, Sputnik 1 se convertía en el primer satélite artificial puesto en órbita de la historia. Desde entonces, son cientos los dispositivos que han seguido sus pasos. Tantos que a día de hoy, la órbita terrestre es un espacio atestado de cacharros espaciales en diverso grado de descacharramiento y la basura espacial se ha convertido en un problema que amenaza las actuales operaciones y misiones satelitales.
El pasado 2 de julio, un satélite destinado a medición y seguimiento del hielo de los polos, llamado CrioSat-2, operado por la Agencia Espacial Europea, orbitaba como de costumbre a unos 700 metros de altura de la superficie terrestre cuando los ingenieros al mando detectaron un trozo de chatarra espacial flotando en su dirección. Siguiendo la trayectoria de ambos objetos, comprobaron que las probabilidades de un impacto no hacían más que aumentar, así que una semana después decidieron poner en marcha su sistema de propulsión y colocar el CrioSat en otra trayectoria. 50 minutos después de completar la maniobra, la chatarra atravesaba su anterior posición a una velocidad aproximada de 4 kms por segundo.
Este tipo de maniobras para evitar accidentes se ha ido volviendo más y más común a medida que aumentaban los satélites, sondas y pedazos de ambos que pueblan nuestra órbita. En 2017, empresas, gobiernos y ejércitos, así como proyectos amateur, lanzaron al espacio 400 satélites, cuatro veces más que la media anual entre 2000 y 2010. Los números pueden incrementarse aun más si empresas como Boeing o SpaceX siguen adelante con planes ya anunciados para colocar ristras de satélites de comunicaciones que igualarán en cantidad a todos los enviados durante toda la historia de la exploración espacial.
Basura zombie, riesgo de colisión
No solo estamos llenando el espacio de basura igual que estamos haciendo con la Tierra. El problema más urgente es que esto puede convertirse en un peligro. En 2009 un satélite comercial estadounidense chocó con un satélite ruso de comunicaciones ya fuera de uso, creando miles de nuevos trocitos de basura con la que otros satélites pueden ahora chocar, y cada movimiento para evitarlos consume combustible que en teoría debe ser utilizado para la misión principal de cada satélite en cuestión. Es como un laborioso videojuego en el que cada vez es más difícil no chocar con algo mientras la fuente de energía, limitada desde el principio, se va agotando.
Basura espacial, un viaje hasta la Tierra. Fuente: ESA
El enemigo, además, tiene algo de zombi. En torno al 95% de los objetos en órbita son satélites inactivos o piezas rotas de los mismos, según Nature. Eso dificulta saber qué características tienen exactamente, algo que sería muy útil a la hora de evaluar riesgos y de navegar en torno a ellos para evitarlos. En esos casos, las agencias espaciales y los ejércitos utilizan los telescopios disponibles para recoger información durante un determinado periodo de tiempo antes de una posible colisión: si se mantiene estable o se mueve sin control, de qué materiales está hecho, si está afilado o es plano… Cuanto más sepan sobre esa chatarra zombi, mejor.
Así que diversos equipos de científicos están probando distintos enfoques para encontrar el modo de solventar el problema. Algunos han optado por hacer un detallado registro de todos los objetos que pululan por la órbita terrestre, en total unos 20.000, detallando su tamaño y forma de manera que los ingenieros de estos proyectos sepan cómo manejar sus satélites alrededor de cada uno en caso de topárselos. Otros están intentando situar todos esos objetos en su respectiva posición para trazar un mapa de la basura espacial. Otros quieren determinar órbitas y trayectorias seguras para los nuevos satélites.
Redes y arpones para pescar chatarra espacial
Algunos están buscando métodos para reducir la cantidad de chatarra que flota en la órbita terrestre, y uno de esos proyectos se ha planteado pescarla como si fuesen cachalotes y viviésemos en el siglo XIX: a base de redes y arpones. El proyecto se llama RemoveDEBRIS, ha sido desarrollado por la Universidad de Surrey, en Reino Unido, y va a realizar 4 experimentos en los que va a poner a prueba algunos conceptos y posibilidades que podrían ayudar a reducir la cantidad de escombros que pululan en la órbita más baja de la Tierra con un coste moderado.
RemoveDEBRIS, vídeo de la misión. Fuente: Universidad de Surrey.
Con un presupuesto de 15 millones de euros, esos experimentos se realizarán en un periodo de pocos meses. La nave será lanzada hacia la Estación Espacial Internacional en abril y colocada en posición en junio. El 16 o 17 de septiembre de 2019 pondrá en marcha la primera prueba, en la que utilizará una red: lanzará un satélite en forma de cubo, un cube sat, del tamaño aproximado de una caja de zapatos de la que luego saldrá un globo que se hinchará hasta alcanzar un diámetro aproximado de 1 metro. RemoveDEBRIS tratará luego de atraparlo lanzando una red con unos pesos para mantenerlo dentro.
El segundo experimento tendrá lugar a finales de octubre, y en este lanzará otro cubo y utilizará un sistema de rayos láser para escanearlo y aprender de él todo lo posible, además de encontrar la forma de navegar a su alrededor.
En el tercero, calculado para principios de febrero de 2020, RemoveDEBRIS extenderá un brazo robótico de un metro y medio, colocará un plato como objetivo y lanzará contra él un arpón para dejarlo enganchado.
El cuarto y último se espera que se realice en marzo. Para su última prueba, el satélite desplegará un mástil y una vela, que servirá como sistema de impulso para hacer descender al objeto hasta una altura menor, donde finalmente se desintegrará por la fricción contra la atmósfera.
Referencias
Satellite studying Earth’s diminishing ice swerves to avoid collision – Rocket Science Blog, ESA.
Kaputnik chaos could kill Hubble – Nature
The quest to conquer Earth’s space junk problem – Nature
Stand back, Aquaman: Harpoon-throwing satellite takes aim at space junk – Nature
RemoveDEBRIS – University of Surrey
Sobre la autora: Rocío Pérez Benavente (@galatea128) es periodista
El artículo Redes y arpones para cazar basura zombie en el espacio se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Javier Fernández Panadero: “La ciencia no te sirve en la vida cotidiana porque no la conoces”
La ciencia es difícil, a veces, muy difícil. Pero si te dicen que su conocimiento te puede salvar de morir por asfixia en un incendio o convertirte en la persona más habilidosa de la tierra cuando en realidad eres un patoso es posible que tu perspectiva cambie de forma sustancial.
Eso es justamente lo que se ha propuesto el físico Javier Fernández Panadero en su charla “Ha llegado el cacharrista”, desarrollada en la octava edición del evento de divulgación científica Naukas Bilbao, celebrado del 13 al 15 de septiembre en el Palacio Euskalduna de Bilbao.
 Imagen: El físico Javier Fernández Panadero durante su charla en Naukas Bilbao 2018. (Fotografía: Iñigo Sierra)
Imagen: El físico Javier Fernández Panadero durante su charla en Naukas Bilbao 2018. (Fotografía: Iñigo Sierra)La intervención de Fernández Panadero ha permitido comprobar como la combinación del conocimiento científico con la mirada de un ingeniero puede ser la solución a una situación de emergencia.
“La ciencia no me vale para nada porque yo no compro logaritmos de patatas, dicen algunos, pero en realidad la ciencia no te sirve en la vida cotidiana porque no la conoces”, ha asegurado Fernández, que ha convertido su intervención en la demostración empírica de que una persona corriente sumada a unos conocimientos científicos puede ser MacGyver.
Fernández, que es profesor de tecnología en secundaria y un apasionado de la divulgación científica, ha transformado un sujetador en una mascarilla contra humo y polvo que te puede salvar la vida si tienes la mala suerte de verte envuelto en un derrumbamiento o un incendio y ha demostrado que el papel de aluminio puede ser la solución cuando necesitas una pila grande y solo tienes baterías chiquitinas.
Estos experimentos, extraídos de su libro “Como Einstein por su casa”, tienen un mismo hilo conductor: “utilizar los experimentos no solo para ilustrar conceptos científicos, sino para encontrar soluciones a situaciones caseras”.
A través de sus exhibiciones, Fernández Panadero ha dejado claro que solo alguien que conoce bien las propiedades de la seda dental sabe que se trata de una herramienta perfecta para cortar un bizcocho con la precisión de un cirujano “y no desmenuzarlo como sucedería con un cuchillo romo”.
“A veces se confunde la ciencia básica, la que sirve para generar conocimiento, con el planteamiento de un ingeniero que busca su aplicación. Aunque uno no sea hábil si incorpora protocolos se convierte en alguien hábil”, razona.
Desde luego con “cacharrerismo” la física y la ciencia saben mucho mejor.
Sobre la autora: Marta Berard, es periodista en la agencia de comunicación GUK y colaboradora de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Javier Fernández Panadero: “La ciencia no te sirve en la vida cotidiana porque no la conoces” se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Moscas, pan de molde, plastilina y…¡Eureka!
La matemática Clara Grima explica qué son los escutoides en la primera jornada de Naukas Bilbao 2018.
Esta vez no ha sido en una bañera, como en el caso de Arquímedes, sino entre moscas de la fruta, figuras de plastilina y rebanadas de pan de molde, porque estas han sido las herramientas escogidas por la profesora de la Universidad de Sevilla Clara Grima para explicar ante una audiencia ávida de conocimiento científico qué son los escutoides y por qué su su descripción geométrica es tan relevante para la biología, la medicina y las matemáticas.
 Imagen: La matemática Clara Grima durante su charla en Naukas Bilbao 2018. (Fotografía: Iñigo Sierra)
Imagen: La matemática Clara Grima durante su charla en Naukas Bilbao 2018. (Fotografía: Iñigo Sierra)Todo ha sucedido en la primera jornada del evento de divulgación científica Naukas Bilbao, que este año ha celebrado su octava edición en el Palacio Euskalduna de Bilbao, un escenario en el que Grima ha conseguido unir en una misma charla moscas, diagramas matemáticos y biología celular.
“Hemos descrito la forma geométrica de las células epiteliales. Se creía que eran prismas que encajaban como piezas de lego, pero si eso fuera así en las superficies de forma curva saltarían”, ha asegurado Grima. Esas nuevas figuras, cuya geometría no había sido descrita hasta que el grupo de investigadores, liderados por el profesor del Departamento de Biología Celular de la Universidad de Sevilla Luisma Escudero, se puso manos a la obra, son los escutoides.
Pero para comprender su relevancia es clave definir el concepto de epitelio: se trata de un tejido grueso que recubre las superficies de los organismos vivos y que puede ser comparado a “una rebanada de pan de molde”.
Escudero, Grima y el resto del equipo, formado por biólogos, matemáticos y físicos, han conseguido describir cómo es la figura geométrica tridimensional que adoptan las células epiteliales para crear los órganos y generar vida. Y lo han hecho a través de la observación de la saliva de las moscas de la fruta y mediante el uso de una estructura matemática conocida como diagramas de Voronoi.
“La forma de las células epiteliales son los escutoides, que son como unos prismas retorcidos que se abrazan. Luisma los ha representado con la plastilina de su hija Margarita”, ha precisado Clara.
 Imagen: Escutoides. (Fuente: Naukas.com)
Imagen: Escutoides. (Fuente: Naukas.com)La nueva figura descrita explica que las células de los tejidos epiteliales se puedan plegar, adoptar distintas curvaturas y crear órganos que funcionen correctamente. Este hallazgo, que ha sido publicado en la prestigiosa revista científica Nature Communications, cobra relevancia porque contribuye al desarrollo de las ciencias de la salud y puede ayudar en el diseño de tejidos biónicos mediante tecnologías digitales.
Pero además, el descubrimiento permitirá establecer el dibujo de un epitelio sano y disponer de ese modelo resultará útil para compararlo con tejidos reales y detectar anomalías en el crecimiento de las células, lo que llevaría a disponer de nuevas herramientas para el diagnóstico de enfermedades.
“La propia geometría de la naturaleza es la que te dice que las cosas no van bien”, ha añadido Grima con entusiasmo.
Y así, entre moscas, rebanadas de pan y diagramas de Voronoi es como se han descubierto los escutoides. Los responsables de la investigación atribuyen el nombre a la similitud que la nueva figura descubierta tiene con el tórax del escarabajo, denominado scudum, pero Clara ha confesado: “la verdad, verdadera es que viene de (Luisma) Escudero, porque él fue el primero en reclamar que la teoría comúnmente aceptada no encajaba”. Eso y que la plastilina era de su hija.
Sobre la autora: Marta Berard, es periodista en la agencia de comunicación GUK y colaboradora de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Moscas, pan de molde, plastilina y…¡Eureka! se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Los ecosistemas acuáticos de África y el cambio climático
 Río Congo. Foto: Berto Saltori / Flickr Creative Commons
Río Congo. Foto: Berto Saltori / Flickr Creative CommonsEl cambio climático es ya una de las principales causas de la alteración y el deterioro de los ecosistemas y la biodiversidad. El Quinto Informe de Evaluación del Grupo Intergubernamental de Expertos sobre el Cambio Climático de las Naciones Unidas afirma que los ecosistemas africanos ya están viéndose afectados de manera importante por el cambio climático y que se espera que los impactos futuros sean aún más considerables. En este contexto, resulta necesario entender cómo la gestión y mejora de los servicios ecosistémicos, entendidos como la multitud de beneficios que la naturaleza aporta a la sociedad, puede fomentar la capacidad de una sociedad para adaptarse al cambio climático.
Las investigadoras Laetitia Pettinoti del Basque Centre for Climate Change (BC3), Amaia de Ayala de la UPV/EHU y BC3 y Elena Ojea de la Universidad de Vigo han realizado un estudio sobre la importancia que tienen los beneficios de los ecosistemas acuáticos en África para la adaptación al cambio climático.
Los servicios ecosistémicos acuáticos son aquellos que provienen o dependen del agua, ya sea salada o dulce. ‘Nuestro estudio se ha centrado en los ecosistemas de cuencas hidrográficas como los humedales, bosques ribereños, manglares, llanuras de inundación y ríos. Estos ecosistemas proporcionan distintos servicios como provisión de alimento, materias primas, agua y medicamentos, mantenimiento de la calidad del suelo y hábitats, control de inundaciones y promoción del ocio y la cultura’ explica Amaia de Ayala.
África, muy vulnerable al cambio climáticoEl estudio se centra en África por tres razones principales: los flujos de los ríos son esenciales para proveer servicios ecosistémicos necesarios para millones de medios de vida en el continente, África presenta una alta vulnerabilidad al cambio climático lo que conlleva la necesidad de una solución política, y la investigación sobre la relación entre los servicios de los ecosistemas y el cambio climático es escasa. “De esta manera los resultados obtenidos en nuestra investigación proporcionan orientación en el diseño de políticas de adaptación al cambio climático en el continente africano” señala Amaia de Ayala.
Las investigadoras han revisado hasta 36 estudios de valoración de la últimas tres décadas llevados a cabo en África y han creado una base de datos de 178 valores monetarios de servicios ecosistémicos acuáticos. Esto les ha permitido llevar a cabo por primera vez un meta-análisis para África.
El estudio concluye que los países más vulnerables al cambio climático presentan una mayor degradación de su biodiversidad y ecosistemas. Produciéndose, además, un círculo vicioso ya que a mayor degradación de sus ecosistemas, más vulnerables son a los efectos del cambio climático. El PIB per cápita está positivamente relacionado con el valor de los servicios ecosistémicos, mientras que el porcentaje de pobreza rural tiene un efecto negativo sobre ellos.
‘Por tanto, dado que los países menos vulnerables poseen por un lado, una brecha de adaptación menor y, por otro lado, valores de servicios ecosistémicos acuáticos mayores, este estudio sugiere que la adaptación basada en ecosistemas puede ser una medida clave para la adaptación al cambio climático en África’ concluye Amaia de Ayala.
La adaptación basada en los ecosistemas engloba el uso de la biodiversidad y los beneficios de los ecosistemas como parte de una estrategia general de adaptación para ayudar a las personas a adaptarse a los impactos adversos del cambio climático. Dicho de otra forma, utiliza la “infraestructura verde” y los beneficios que aportan los ecosistemas para fomentar la resiliencia de las sociedades humanas al cambio climático. De hecho, 25 países africanos ya han incorporado en sus Programas Nacionales de Acción para la Adaptación al cambio climático la adaptación basada en ecosistemas.
Referencia:
Laetitia Pettinotti, Amaia de Ayala and Elena Ojea (2018) Benefits From Water Related Ecosystem Services in Africa and Climate Change Ecological Economics DOI: 10.1016/j.ecolecon.2018.03.021
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Los ecosistemas acuáticos de África y el cambio climático se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:La ciencia y la guerra
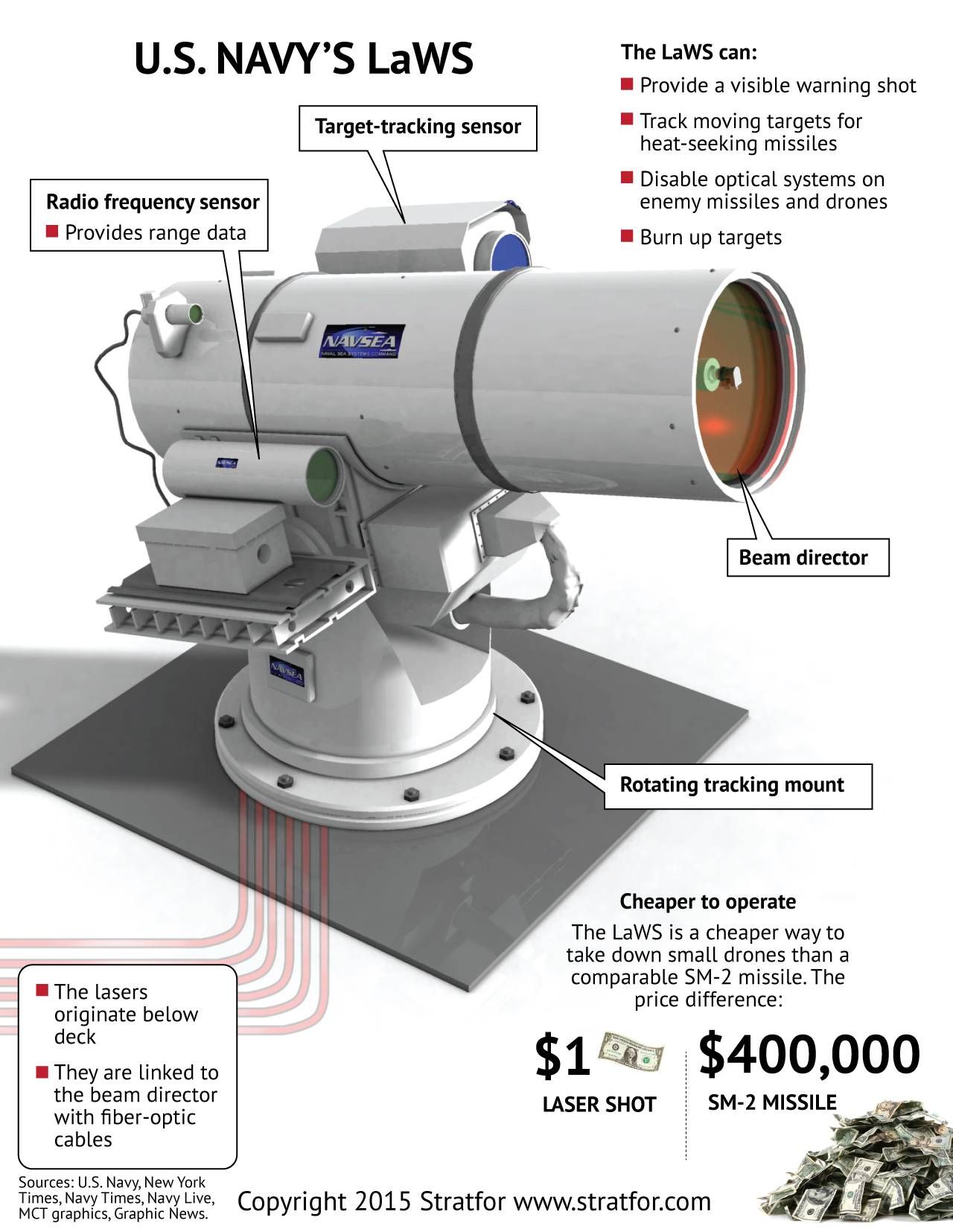
El conflicto bélico es uno de los múltiples ámbitos en los wue se han aplicado los conocimientos de la ciencia, desde tiempo inmemorial. Si el primer uso de la nueva tecnología de la piedra afilada fue destazar animales muertos seguro que el segundo fue abrirle la cabeza al congénere de la tribu de al lado. O viveversa. Y esto es porque, como demuestra la primatología, la guerra estaba con nosotros antes que el saber.
Nuestros parientes chimpancés son capaces de organizarse en bandos, combatir, matar e incluso de llevar adelante campañas de exterminio sin necesidad de lanzas, espadas o fusiles. Basta el fuerte sentido intragrupal y una causa, a veces no muy sólida, para iniciar el conflicto. Y nada de combates rituales o simulacros de batallas: se va a la masacre. Para lo cual no hace falta trigonometría, sino fuerza y mala leche.
No, la ciencia no provoca las guerras, aunque pueda hacerlas más ‘eficientes’ en destrucción y muerte o poner en marcha mecanismos políticos que la hagan inevitable. Quienes luchan contra el conocimiento para evitar las guerras se equivocan, porque ni siquiera la decisión de usar tecnología para matar se toda desde criterios científicos. Y existen alentadores ejemplos de técnicas concretas que se han limitado gracias a la presión de los científicos y el resto de la sociedad por los horrores que provocan. Las armas químicas o nucleares se han usado, aunque poco, por sus efectos: este es el camino.
Prohibir el desarrollo de nuevas áreas de la ciencia para evitar su uso bélico no sólo evita que aparezcan malos desarrollos, sino también buenos. Nunca hay modo de saber cuál será el destino de un nuevo conocimiento. Pero es que además es una forma de automutilación intelectual: lo que no se descubre no se conoce jamás. Es cierto que alunos rincones del universo albergan horrores, y es prudente acercarse y tratalos con precaución. Pero el sistema más seguro es ejercer la vuluntad y decidir no utilizar aquello que sea excesivo para nuestra compasión. Nunca la prohibición y la ausencia voluntaria de saber.
Sobre el autor: José Cervera (@Retiario) es periodista especializado en ciencia y tecnología y da clases de periodismo digital.
El artículo La ciencia y la guerra se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Un mapa del discernimiento
Creo que entre los muchos mapas de los que ha hablado Raúl Ibáñez en este cuaderno, se le ha olvidado al menos uno: el mapa del discernimiento.
 “Une carte du sens” –Un mapa del discernimiento– extraído de [1]. En la página 180 de [2] puede verse una versión en inglés.
“Une carte du sens” –Un mapa del discernimiento– extraído de [1]. En la página 180 de [2] puede verse una versión en inglés.
Pero empecemos por el principio. Prédire n’est pas expliquer –Predecir no es explicar (Editions Eshel, 1991)– es el título de una serie de entrevistas que el matemático René Thom (1923-2002) mantuvo con Emile Noël. En este texto, Thom explicaba la génesis de su teoría de las catástrofes y exponía sus posiciones filosóficas sobre la ciencia.
En una parte de este escrito, el Medalla Fields describía una comida que compartió con el psiquiatra Jacques Lacan (1901-1981). Durante ese almuerzo, el psicoanalista invitó a Thom a hablar sobre su percepción de las matemáticas, sobre la evolución de sus ideas y sobre su relación con el concepto de matema. Al final de la comida, René Thom lanzó este pensamiento: “La verdad no está limitada por la falsedad, sino por insignificancia”.
El matemático realizó posteriormente un dibujo intentando aclarar y matizar esta afirmación, el que aparece en la imagen que inicia este escrito.
Debajo se reproduce la traducción del texto que aparece en [1] en el que René Thom explica los lugares de este especial mapa:
En la base se encuentra un océano, el Mar de la Insignificancia. En el continente, la Verdad se sitúa a un lado, la Falsedad en el otro. Están separadas por un río, el Río del Discernimiento. De hecho, lo que separa la verdad de la falsedad es la facultad de discernimiento. Es una noción que se debe a Aristóteles: la capacidad para la contradicción. Es lo que nos separa de los animales: cuando ellos reciben una información, la aceptan instantáneamente y desencadena la obediencia a este mensaje. Los seres humanos, sin embargo, tienen la capacidad de retractarse y cuestionar su veracidad.
Siguiendo la orilla de este río, que desemboca en el Mar de la Insignificancia, se viaja a lo largo de una costa que es ligeramente cóncava: en un extremo se encuentra la Ciénaga de la Ambigüedad y en el otro extremo se halla el Pantano del Perogrullo. Al frente del delta del río, se ve la Fortaleza de la Tautología: Ese es el baluarte de los lógicos. Se sube una muralla hacia un pequeño templo, una especie de Partenón: estas son las Matemáticas.
A la derecha, se encuentran las Ciencias Exactas: en las montañas que rodean la bahía se sitúa la Astronomía, con un observatorio que corona su templo; en el extremo derecho se hallan las máquinas gigantes de la Física, los anillos del acelerador en el CERN; los animales en sus jaulas señalan los laboratorios de Biología. Fuera de todo esto emerge un arroyo que se alimenta en el Torrente de la Ciencia Experimental y que desemboca en el Mar de la Insignificancia.
A la izquierda hay un camino ancho que sube hacia el noroeste, llega hasta la Ciudad de las Artes y las Ciencias Humanas. Continuando a lo largo de ella, se llega a las laderas del Mito. Hemos ingresado en el reino de la Antropología. Arriba, en la parte superior, se encuentra la Altiplano del Absurdo. La columna vertebral significa la pérdida de la capacidad de discernir contrarios, algo así como un exceso de comprensión universal que hace que la vida sea imposible.
Según comenta el propio Thom en [1], Une carte du sens –este mapa del discernimiento– imita la Carte du Tendre, el mapa de un país imaginario llamado Tendre que aparece en la novela Clélie, histoire romaine de la escritora Madeleine de Scudéry (1607-1701). Este mapa es una ‘representación topográfica y alegórica de la conducta y de la práctica amorosa’…
 “Carte du Tendre” de François Chauveau. Wikimedia Commons.
“Carte du Tendre” de François Chauveau. Wikimedia Commons.Referencias
[1] The Map of Discernment, Futility Closet, 22 julio 2018
[2]Roy Lisker, René Thom. Interviews with Emile Noël, traducción de Prédire N’est Pas Expliquer, 2010
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo Un mapa del discernimiento se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Cristalografía (12): In vino veritas

Según la mitología griega fue el mismísimo dios Dionisios el que descendió del Monte Olimpo para enseñar a los hombres a fabricar vino. Según la arqueología moderna ese descenso, de haber existido, habría tenido lugar en Asia Menor (en lo que hoy es el este de Turquía) hace unos 7.000 años. Junto con el arte del vino, Dioniso donó otro regalo que pasó mucho tiempo sin ser reconocido como tal, el tártaro, que se encuentra en el fondo de, entonces, las ánforas y, hoy, las barricas de vino.
Tanto Lucrecio como Plinio el viejo estaban familiarizados con el tártaro. Lo que hoy sabemos que es tartrato ácido de potasio (formalmente hidrógeno tartrato de potasio) era descrito como de sabor agrio y que ardía con una llama de color púrpura, además de proporcionar recetas para una docena de remedios que lo contenían.
Se estudió con más detalle en la Edad Media. El alquimista persa Abū Mūsa Ŷābir ibn Hayyan al-Āzdī (conocido en Europa como Geber) fue el primero en dejar constancia por escrito, alrededor del año 800, de que el tártaro es una sal y aisló el ácido tartárico (y otra buena cantidad de compuestos orgánicos, pero esa es otra historia) aunque no con demasiada pureza. Hubo que esperar a 1769 para obtener el ácido tartárico químicamente puro, cosa que logró Carl Wilhelm Scheele (a la par que otra buena cantidad de compuestos orgánicos). El compuesto se empleaba en la fabricación de cosméticos y remedios medicinales, como la sal de la Rochelle o el tártaro emético, por lo que muchas bodegas se convirtieron de facto en fábricas de ácido tartárico.

Alrededor de 1818, Paul Kestner, un productor de tártaro de Thann (Francia) se dio cuenta de que, además de ácido tartárico se producía en sus barriles una pequeña cantidad de cristales de lo que parecía otra sustancia. Al principio pensó que podría ser ácido oxálico; sin embargo, al poco tiempo se dio cuenta de que era algo nuevo y empezó a producirlo en cantidades mayores a base de hervir disoluciones saturadas de ácido tartárico. En 1826, convencido completamente de que era algo desconocido para la ciencia, se decidió a llevar una muestra a Gay-Lussac, quien, después de repetidos experimentos, llegó a la conclusión de que su fórmula era C4H6O6, la misma del ácido tartárico. Llamó a este nuevo compuesto ácido racémico (del latín racemus, esto es, racimo de uvas).
Las diferencias químicas entre los ácidos tartárico y racémico (y entre sus sales , tartratos y racematos) eran pequeñas, pero suficientes como para tener intrigados a los químicos. Este fue uno de los casos de isomería conocidos en la época; además muchas de las sales de los dos ácidos eran isomorfas.

Un aspecto importante en lo trascendencia que llegaron a tener estos ácidos en el desarrollo de la ciencia fue su bajo coste y la facilidad de obtención en una época, principios del XIX, en la que la industria química estaba en su infancia y los productos químicamente puros eran una rareza. Además racematos y tartratos eran muy fáciles de preparar y conseguir cristales de tamaño apreciable no era nada complicado. Por lo tanto, era el sistema perfecto en el que estudiar dos conceptos nuevos pero que no se terminaban de entender, y que había indicios de que podían estar relacionados: isomería e isomorfismo.
En los años posteriores a 1830 Biot midió la actividad óptica del ácido tartárico y sus sales (dextrógiros todos ellos); el racémico y las suyas eran ópticamente inactivas. Berzelius, empeñado en encontrar una explicación al fenómeno, instó a Mitscherlich, ya una autoridad en la química cristalina, a que estudiase la simetría de tartratos y racematos.
Mitscherlich confirmó los hallazgos de Biot, el tartárico y sus sales eran todos dextrógiros y sus cristales hemiédricos; el racémico y las suyas inactivos ópticamente y sus cristales holoédricos. Había dos sales que no cumplían estas reglas generales: el tartrato de sodio y amonio y el racemato de sodio y amonio que formaban cristales idénticos pero de actividad óptica de signo opuesto. Mitscherlich estaba tan confundido por este hecho al que no era capaz de encontrar una explicación que no publicó sus resultados en más de una década. Sólo lo haría en 1844, después de que en 1841 Frédéric Hervé de la Provostaye publicase un estudio similar.
El misterio sería resuelto en 1848 por un joven y desconocido profesor de Dijon, recién doctorado, Louis Pasteur.
Referencias generales sobre historia de la cristalografía:
[1] Wikipedia (enlazada en el texto)
[3] Molčanov K. & Stilinović V. (2013). Chemical Crystallography before X-ray Diffraction., Angewandte Chemie (International ed. in English), PMID: 24065378
[4] Lalena J.N. (2006). From quartz to quasicrystals: probing nature’s geometric patterns in crystalline substances, Crystallography Reviews, 12 (2) 125-180. DOI:10.1080/08893110600838528
[5] Kubbinga H. (2012). Crystallography from Haüy to Laue: controversies on the molecular and atomistic nature of solids, Zeitschrift für Kristallographie, 227 (1) 1-26. DOI: 10.1524/zkri.2012.1459
[6] Schwarzenbach D. (2012). The success story of crystallography, Zeitschrift für Kristallographie, 227 (1) 52-62. DOI: 10.1524/zkri.2012.1453
Este texto es una revisión del publicado en Experientia docet el 30 de enero de 2014
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Cristalografía (12): In vino veritas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:La regulación de la diuresis en mamíferos
Al contrario que otros vertebrados, los mamíferos (salvo algunas especies, como los dromedarios) no ajustan la producción de orina modificando la tasa de filtración glomerular (GFR). De hecho mantienen esta relativamente constante y modifican la fracción de la orina primaria que es reabsorbida antes de su evacuación al exterior para regular el volumen y la concentración osmótica de los fluidos corporales.
Un porcentaje relativamente alto de la orina primaria –entre un 60% y 80% del volumen- es reabsorbido desde el túbulo contorneado proximal, para lo cual se reabsorben activamente porcentajes similares de NaCl. Además de la sal y el agua, glucosa, aminoácidos y bicarbonato son también reabsorbidos en ese segmento, estos prácticamente en su totalidad.
La reabsorción de Na+ se produce gracias a la actividad de una ATPasa de Na+-K+ de la membrana basolateral del epitelio (la que separa el líquido intersticial del interior celular). Ese transporte genera un gradiente electroquímico en la membrana apical (la que separa el interior celular de la luz del túbulo) que favorece la entrada de sodio desde el fluido tubular. La reabsorción de agua se produce a través de aquaporinas estructurales, que se hallan siempre presentes en esas células (su presencia apenas depende de factores externos).
Tras pasar por el túbulo proximal, la orina penetra en el asa de Henle. Lo hace con una concentración osmótica de unos 300 mOsm, pero tras su recorrido por ese segmento, puede alcanzar el túbulo distal con una concentración inferior a la anterior (puede llegar a ser de 100 mOsm). Como vimos, esa diferencia es debida al transporte activo de NaCl que tiene lugar en la rama ascendente, que lo retira de la orina, disminuyendo en ella su concentración, a la vez que aumenta la del líquido intersticial.
Tras el asa de Henle la orina accede al túbulo contorneado distal. El epitelio de ese segmento transporta NaCl activamente de la luz del túbulo al especio intersticial. Y aunque no es impermeable, es poco permeable al agua.
Lo que ocurre a continuación en el tubo colector depende de cuáles son las necesidades hídricas del organismo. Si necesita retener agua, el organismo se encuentra en estado de antidiuresis y el riñón producirá un volumen de orina muy limitado. Eso es consecuencia de una intensa reabsorción de agua en el tubo colector, reabsorción que se produce gracias a la presencia en la membrana apical de las células de la pared del tubo de numerosas moléculas de una forma de aquaporina (AQP-2) específica de ese epitelio. Recordemos que debido al transporte activo de NaCl que tiene lugar en la rama ascendente del asa de Henle y al equilibrio iónico y osmótico que se establece entre su rama descendente y el fluido intersticial de la médula renal, la concentración osmótica de ese fluido en el interior medular es muy alta. Por ello, la presencia de numerosos poros en las membranas apicales de las células de la pared del tubo colector permiten que el agua pase con gran facilidad de un fluido que se encuentra originariamente a una concentración osmótica muy baja (la orina que llega del túbulo distal) a otro con la concentración osmótica muy alta (el fluido intersticial medular). Y eso ocurre hasta que ambas concentraciones osmóticas se igualan, para lo que debe pasar un volumen muy importante de agua. Además, a lo largo del tubo colector se sigue reabsorbiendo activamente NaCl, lo que favorece aún más este proceso. Como consecuencia de esa reabsorción, la orina final puede llegar a representar tan solo un 1% del volumen de plasma filtrado en el glomérulo y alcanzar una concentración osmótica de 1200 mOsm, que es cuatro veces más alta que la del plasma. Pero en mamíferos con grandes restricciones hídricas esa concentración puede llegar a multiplicarse por diez o más. Producen mínimas cantidades de orina y evitan así perder agua por esa vía.
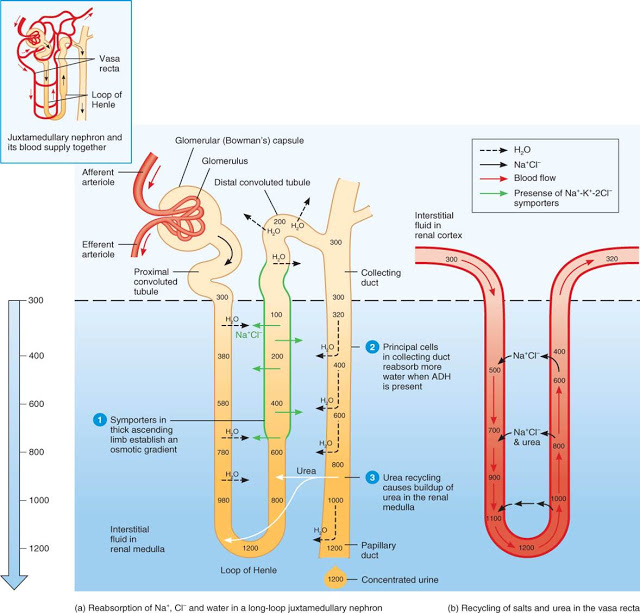
Ese estado de antidiuresis a que me he referido en el párrafo anterior es el que se produce cuando hay una alta concentración sanguínea de la hormona antidiurética (ADH), que en mamíferos es la arginina vasopresina (AVP). Es ella la responsable de la presencia en las células de la pared del ducto de numerosas unidades de aquaporinas AQP-21. Por ello, cuando las condiciones cambian y no hay necesidad de ahorrar agua o, incluso, conviene eliminarla, deja de secretarse ADH desde la neurohipófisis, baja su concentración sanguínea y, como consecuencia de ello, las aquaporinas son retiradas de la membrana apical de las células del epitelio del tubo colector. Disminuye así su permeabilidad al agua (llega a hacerse virtualmente impermeable) y deja de reabsorberse agua desde el interior del tubo hacia los espacios intersticiales. El volumen de orina es muy alto y su concentración osmótica, muy baja. De hecho, en seres humanos esa concentración puede ser tan baja como 50 mOsm, o sea, seis veces más baja que la plasmática, y el volumen de orina producido elevarse hasta representar un 15% del plasma filtrado en el glomérulo. Merece la pena reparar en el hecho de que una concentración osmótica de la orina tan baja no es solo el resultado de la supresión de la reabsorción de agua desde el tubo colector, sino que es necesario que se produzca una importante reabsorción de NaCl que no vaya acompañada de la correspondiente reabsorción de agua.
La ADH no es la única hormona implicada en la regulación de la función renal en mamíferos. La aldosterona y el péptido natriurético auricular cumplen también un importante papel. Antes de exponer brevemente en qué consiste, conviene advertir que tanto la aldosterona como, en general, las hormonas natriuréticas, o hormonas de similares naturaleza y efectos, se hallan en muchos otros grupos, además de mamíferos, pero su papel se entiende mejor en este contexto.
La aldosterona promueve la recuperación de Na+ desde la orina primaria y también la secreción de K+. Por ello, su efecto global más obvio es regular el contenido de esos iones en los fluidos corporales. Sin embargo, de forma indirecta también cumple un papel determinante en la regulación del volumen de los fluidos extracelulares, plasma sanguíneo incluido. La razón es que la concentración osmótica y de sales, como sabemos, se halla estrechamente controlada en los mamíferos y, en general, en el resto de los vertebrados. Por ello, el volumen de agua extracelular es muy dependiente de la cantidad de NaCl que hay en esos fluidos (no así en los intracelulares, cuyo catión principal es el K+), ya que Na+ y Cl– son los principales iones extracelulares. Así pues, si una hormona, como la aldosterona, promueve la reabsorción de Na+, también promueve la de Cl– y, por supuesto, la de agua. En otras palabras: cuanto más Na+ se reabsorbe en el riñón, también se reabsorbe más agua, por lo que su efecto neto es antidiurético.
La aldosterona es una hormona esteroidea, un mineralocorticoide producido por la corteza adrenal. Su secreción está controlada por otro sistema hormonal, el sistema renina-angiotensina que, a su vez, se encuentra parcialmente controlado por receptores de presión sanguínea y de volumen sanguíneo. Cuando la presión de la sangre baja y en virtud de varios mecanismos que actúan simultáneamente, las células yuxtaglomerulares (células especializadas del endotelio de la arteriola aferente) liberan renina. La acción (enzimática) de la renina sobre una molécula precursora de origen hepático (el angiotensinógeno) acaba dando lugar a que se produzca una sustancia denominada angiotensina II. Esta ejerce varios efectos: estimula la constricción (estrechamiento) de arteriolas sistémicas; promueve la sed; estimula la secreción de ADH y estimula la secreción de aldosterona. Todas las actuaciones provocadas por la angiotensina II causan la recuperación de agua y el reestablecimiento de la presión sanguínea y el volumen de líquidos extracelulares adecuados. Cuando la acción de la renina ha surtido sus efectos, ciertas sustancias paracrinas producidas por las células de la macula densa2 provocan que las células yuxtaglomerulares dejen de liberar renina.
La aldosterona actúa penetrando en sus células diana (a los efectos de lo que nos interesa aquí se trata de las células del epitelio del túbulo distal), llega al núcleo e inicia la transcripción de ADN para producir nuevas ATPasas de Na+-K+ y de canales de Na+ y de K+ para su inserción en la membrana celular. De esta forma se eleva la reabsorción tubular de Na+ y como consecuencia, la recuperación de agua y la restauración del volumen sanguíneo. Este mecanismo actúa, de hecho, en respuesta a situaciones –como las hemorragias- en las que se produce una importante pérdida de líquido sin que ello vaya asociado a una elevación de la concentración osmótica sanguínea.
Hay gran diversidad de péptidos natriuréticos en el dominio animal, y el mejor conocido es el péptido natriurético auricular (ANP, por sus siglas en inglés) de los mamíferos. El ANP se produce en determinadas zonas del encéfalo y en el corazón (de ahí su nombre “auricular”) y sus efectos son en gran parte opuestos a los de la aldosterona. Inhibe, de hecho, la liberación de aldosterona y promueve directamente la secreción de Na+, elevando la producción de orina y la concentración de Na+ en esta. La secreción de ANP es estimulada por el aumento del volumen de líquidos extracelulares, lo que es detectado a partir del estiramiento de las paredes de la aurícula en el corazón.
En definitiva, la función renal está sometida a un complejo sistema de regulación principalmente endocrino. Aquí hemos visto los tres sistemas principales, cada uno con sus especificidades. Gracias a ese sistema de efectos múltiples, los mamíferos, y demás vertebrados, son capaces de mantener estrechamente controlados tanto el volumen de los líquidos corporales, como sus concentraciones osmóticas e iónicas.
Notas:
1El mecanismo es muy similar al que vimos para la mayor parte de vertebrados, aunque en los otros grupos de vertebrados la ADH actúa en el túbulo distal y la molécula de efectos antidiuréticos en los demás vertebrados era algo diferente: arginina vasotocina (AVT).
2Grupo de células especializadas que se disponen en el punto en que el túbulo distal y la arteriola aferente se encuentran en posición adyacente.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo La regulación de la diuresis en mamíferos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La regulación osmótica e iónica en los teleósteos marinos
- La función del asa de Henle en el riñón de mamíferos
- La regulación osmótica de los animales de agua dulce
Una vida eterna
Sabíamos que en unas cuantas especies animales los individuos viven más y se encuentran en mejor estado de salud si se les reduce la ingesta de alimento. Pero no acabábamos de saber si esa misma forma de prolongar la vida sería aplicable a los seres humanos. Seguimos sin saberlo, pero una investigación cuyos resultados se publicaron hace unas semanas en la revista Cell Metabolism parece aportar algunas claves del mecanismo que permitiría que la (así llamada) restricción calórica pudiese alargar la vida de quienes la experimentan.
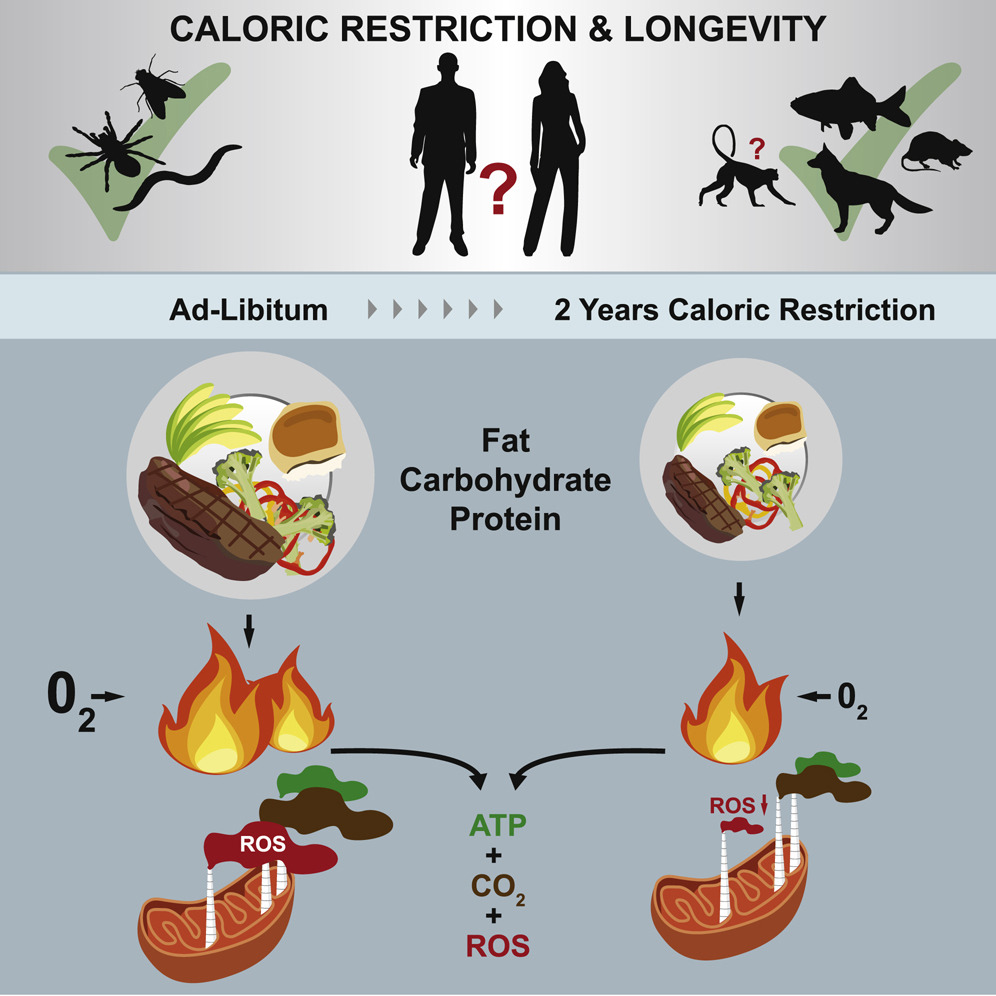
Fuente: Redman et al. (2018) / Cell Metabolism
En la investigación mencionada se limitó la ingestión de alimento a treinta y cuatro personas de ambos sexos, y a otras diecinueve que mantuvieron sus hábitos alimenticios se les monitorizó para que sirvieran de control. Todos los participantes en el estudio eran adultos, ninguno era obeso y, por supuesto, eran voluntarios. Redujeron su ingesta en un 15%, pero se aseguraron una toma adecuada de los nutrientes esenciales.
Dos años después de iniciado el experimento habían perdido 9 kg de peso, mientras que los controles habían ganado 2 kg. Junto con la pérdida de peso, los individuos sometidos voluntariamente a la restricción calórica experimentaron también una importante reducción del gasto metabólico: cada día gastaron entre 80 y 120 kcal menos que las que cabía esperar a partir de la pérdida de peso. O sea, a lo largo de ese periodo de tiempo, la actividad metabólica de los que redujeron la ingesta se adaptó, reduciéndose a niveles inferiores a los característicos de la situación anterior al experimento. Esa adaptación metabólica vino acompañada por una bajada en la actividad de las hormonas tiroideas, que son las principales encargadas de regular el metabolismo. Y también se redujo el denominado “estrés oxidativo”, que es una condición fisiológica perjudicial para las células -y por lo tanto para los órganos y el conjunto del organismo- que se produce como consecuencia de un desequilibrio entre la producción de sustancias oxidantes muy dañinas y la capacidad de los sistemas biológicos para neutralizar esas sustancias o reparar el daño que causan.
Estos resultados refuerzan dos hipótesis sobre las causas del envejecimiento que cuentan con amplia aceptación, la de la velocidad vital (rate of living) y la del daño oxidativo; como veremos, además, ambas son perfectamente compatibles. De acuerdo con la hipótesis de la velocidad vital, que se formuló inicialmente hace cerca de un siglo, la longevidad es inversamente proporcional a la tasa metabólica de un individuo; o sea, cuanto mayor es esa tasa y, por ende, la actividad biológica que refleja, menor es la duración de la vida. Y según la segunda hipótesis, sería el daño que causa el estrés oxidativo al ADN, las proteínas y otras macromoléculas, el responsable del acortamiento de la vida, pues el envejecimiento sería consecuencia de la acumulación de daños. Así pues, bien podría ocurrir que la relación negativa entre actividad metabólica y longevidad viniese mediada por el efecto dañino de las sustancias oxidantes sobre las estructuras biológicas.
En definitiva, el organismo humano se adapta a la privación de alimento reduciendo la velocidad a la que transcurren los procesos vitales. Comer menos conlleva una vida fisiológica más lenta y, en cierto modo, más eficiente. Además, otros estudios han encontrado que un metabolismo basal alto se asocia con un peor estado de salud y mayor riesgo de mortalidad temprana. Por lo tanto, aunque es cierto que este estudio no permite extraer conclusiones firmes y que los datos disponibles no son concluyentes, lo más probable es que comer menos alargue la vida. Eso sí, de lo que podemos estar seguros es de que nos la haría parecer eterna.
Fuente: Leanne M. Redman, Steven R. Smith, Jeffrey H. Burton, Corby K. Martin, Dora Il’yasova & Eric Ravussin (2018): Metabolic Slowing and Reduced Oxidative Damage with Sustained Caloric Restriction Support the Rate of Living and Oxidative Damage Theories of Aging Cell Metabolism 27 (4): 805-815
—————————————————————–
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
————————
Una versión anterior de este artículo fue publicada en el diario Deia el 6 de mayo de 2018.
El artículo Una vida eterna se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Andar puede salvarte la vida
- La historia de la vida
- En la ría palpita la vida, por José Ignacio Saiz Salinas
Nuevas tecnologías para el estudio del cerebro: Desde Cajal a nuestros días

Uno de los objetivos fundamentales de la neurociencia es comprender los mecanismos biológicos responsables de la actividad mental humana. En particular, el estudio de la corteza cerebral constituye el gran reto de la ciencia en los próximos siglos, pues representa el fundamento de nuestra humanidad.
La ciencia ha avanzado de un modo espectacular en las últimas décadas, permitiendo desentrañar algunos de los misterios que encierra el cerebro. Sin embargo, aún no tenemos respuesta a algunas de las principales preguntas de la neurociencia, como por ejemplo: ¿Qué nos hace a las personas humanas? ¿Qué tiene de especial la neocorteza humana? ¿Cómo se altera el cerebro y por qué se produce la esquizofrenia, el Alzheimer o la depresión?
El neurobiólogo y profesor de investigación en el Instituto Cajal (CSIC), Javier de Felipe Orquieta responde a estas cuestiones en la conferencia: “Nuevas tecnologías para el estudio del cerebro: Desde Cajal a nuestros días“. En esta charla Javier de Felipe muestra las distintas líneas de investigación que llevan a cabo proyectos como Blue Brain, Cajal Blue Brain, Human Brain Project o Brain Activity Map para el conocimiento del funcionamiento del cerebro.
La conferencia tuvo lugar el pasado 23 de abril en el Bizkaia Aretoa de Bilbao y forma parte del ciclo de conferencias Achucarro Forum que organiza el centro vasco de neurociencia del mismo nombre para la sensibilización social sobre la investigación de cerebro y sus enfermedades.
'Nuevas tecnologías para el estudio del cerebro:desde Cajal a nuestros día'Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Nuevas tecnologías para el estudio del cerebro: Desde Cajal a nuestros días se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- “La aplicación de las nuevas tecnologías en agricultura” por Pere Puigdomènec
- #Naukas14 Regenerar el cerebro
- Estudio de eficacia escolar en el País Vasco
La energía de las olas ha aumentado un 40 % en el último siglo.
Los convertidores de energía olamotriz son diseñados para generar la máxima energía posible en su ubicación, y toman como referencia un año típico del lugar. Investigadores de diferentes centros de la UPV/EHU han estudiado, junto con el Centro de Investigación de Energía Marina irlandés, la evolución de la energía marina en Irlanda durante el último siglo. Los resultados revelan un incremento de hasta un 40%, lo cual afecta directamente al rendimiento de los convertidores.

Foto: Pete Conroy / Stab Magazine
Los convertidores de energía olamotriz o undimotriz están específicamente diseñados para tener un rendimiento máximo en la ubicación que vayan a tener, es decir, para generar la mayor cantidad de electricidad posible del movimiento de las olas de su entorno. El diseño y adaptación se hace basándose en datos históricos, en la altura y periodo que presentaron las olas en el pasado. “Sin embargo, el espacio de tiempo que se tiene en cuenta suele ser bastante reducido, y, además, se considera el año típico de ese periodo. Así, los convertidores se ajustan en función del comportamiento que deberían tener en ese año típico”, explica Alain Ulazia, profesor de la Escuela de Ingeniería de la UPV/EHU en Eibar .
Teniendo en cuenta los cambios que se están produciendo como consecuencia del cambio climático en cuanto a la temperatura y otros parámetros meteorológicos, Ulazia y otros dos investigadores de la UPV/EHU, de los departamentos de IN y Mecánica de Fluidos y Física Aplicada II, así como de la Estación Marina de Plentzia, en colaboración con el Centro de Investigación de Energía Marina de Irlanda abordaron una investigación de mayor plazo. “Llevamos a cabo en Irlanda un estudio que anteriormente habíamos realizado en el Golfo de Bizkaia, dado que Irlanda es particularmente energética en cuanto a la energía de las olas, y quisimos analizar esa energía como recurso. Calculamos, mediante simulación, qué respuesta o comportamiento habría tenido un convertidor ante el nivel de energía registrado en el último siglo, dividido en periodos de 20 años, dado que los convertidores tienen una vida útil de 20 años de media”, detalla.
Para esta labor, han tenido como fuente de información dos bases de datos del Centro Europeo de Predicción a Plazo Medio (ECMWF): ERA-Interim y ERA20. Ambas son reanálisis, es decir, bases de datos surtidas con multitud de observaciones y mediciones. Son redes espaciales, que proporcionan largas series temporales en cada uno de los ojos de la red, es decir, para cada ubicación. La más conocida es la ERA-Interim, ya que reúne infinidad de datos, incluso provenientes de satélites, pero su limitación es que “solo cuenta con datos de los últimos 40 años —aclara Ulazia—. La ERA20, por su parte, se nutre de muchos menos datos, y es más irregular desde la perspectiva tanto temporal como espacial, pero aporta datos de todo el s. XX”.
En la investigación, calibraron una base de datos contra la otra, valiéndose del periodo de solapamiento que tienen. Y posteriormente las validaron contra las mediciones tomadas en las boyas del Atlántico. Tal como declara Ulazia, “hemos concluido que los datos son aceptables, que se pueden dar por buenos, por lo que hemos podido simular los niveles de energía en los que deberían haber trabajado los convertidores”.

El convertidor olamotriz Oyster, utilizado para el estudio. Foto: Alain Ulazia – UPV/EHU.
Tomando como referencia los 20 años de vida útil media de los convertidores de energía olamotriz, dividieron el siglo pasado en cinco periodos, y adaptaron los conversores para el nivel de energía correspondiente a cada uno de esos periodos. “Encontramos que, del primer periodo de tiempo al último, el nivel de energía marina se ha visto incrementado más de un 40 %, y el incremento mayor se ha dado en los último 20 años (18 %) —subraya el investigador—. No hemos entrado a analizar qué es lo que ha provocado ese aumento, pero la hipótesis principal sería el cambio climático”.
El hecho de que haya grandes oscilaciones en la energía de las olas tiene consecuencias directas en el rendimiento de los convertidores; en la investigación han podido ver, por ejemplo, que “los convertidores no han aprovechado toda la energía que tenían a su alcance, y, además, los eventos extremos, tales como episodios de olas de más de siete metros o fenómenos como El Niño, han sido más frecuentes conforme avanzaba el siglo. Como consecuencia, los convertidores han tenido que entrar más a menudo en modo de supervivencia, y dejar de producir energía mientras duraban estos eventos marinos”, comenta.
La información obtenida debería valer, según Ulazia, para optimizar el diseño de los convertidores: “Como estos dispositivos se optimizan en función de la altitud y el periodo de las olas, habría que adaptar su diseño para que tengan un rendimiento máximo en condiciones que cada vez son más energéticas”.
Referencia:
Markel Peñalba, Alain Ulazia, Gabriel Ibarra-Berastegui, John Ringwood, Jon Sáenz (2018) Wave energy resource variation off the west coast of Ireland and its impact on realistic wave energy converters’ power absorption Applied Energy doi: 10.1016/j.apenergy.2018.04.121
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo La energía de las olas ha aumentado un 40 % en el último siglo. se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Son eficientes las plantas de energía marina?
- Las barreras a los edificios de consumo de energía casi nulo en el sur de Europa
- Se intuye la conservación de la energía (1)

