La caja de resonancia del violín
Sabemos muy bien cómo empujar a una criatura en el columpio del parque: podemos aumentar la amplitud de oscilación de la barquilla sincronizando nuestros empujones con la frecuencia natural de este péndulo. En física se puede fácilmente modelar esta dinámica mediante una sencilla ecuación diferencial y predecir cuál es la frecuencia de resonancia del columpio cargado. Dicho de otra manera: deducimos con exactitud a qué ritmo debemos empujar para que la oscilación del columpio se amplifique; y además sabemos que intentar empujar por encima o por debajo de la frecuencia de resonancia que hemos deducido es inútil, porque la oscilación del péndulo se atenuará. La caja de resonancia de un violín no es más que un columpio algo más complejo que el que acabamos de describir. Debido a sus características constructivas y mecánicas, la caja contiene decenas de frecuencias de resonancia en el rango de las vibraciones sonoras.
 Foto: Roberto Delfanti / Unsplash
Foto: Roberto Delfanti / UnsplashSin una caja de resonancia en un violín, las vibraciones de sus cuerdas apenas son audibles. Así, la transmisión de las vibraciones de las cuerdas al cuerpo hace que tanto la caja como el volumen de aire de su interior empiecen a vibrar también. Debido a las frecuencias naturales de cada uno de los elementos del instrumento y a la unión de todos ellos en el violín, ciertas frecuencias y armónicos superiores de las ondas acústicas se amplifican o se atenúan en mayor o menor medida. De esta manera, se crea el carácter tonal individual de cada violín, que incluye el volumen y el timbre del sonido musical que este consigue.
La invención del violín modernoLa caja de resonancia de los violines fue mejorando a lo largo de los siglos. La lutería es tanto un arte como una ciencia, y todos los maestros artesanos constructores de instrumentos fueron desde sus inicios también científicos empíricos, capaces de aprender y avanzar en su área de conocimiento mediante continuos métodos experimentales de ciencia acústica, prueba y error.
El violín moderno fue construido en Europa a principios del siglo XVI. Entre las principales regiones europeas aspirantes al título de invención del violín están Füssen, en Algovia (hoy parte de Alemania), Sklenařice en la República Checa, Cracovia en Polonia, y, en Italia, Venecia, Brescia y Cremona. De todas ellas, fue Lombardía la cuna de los mejores lutieres, y más en concreto Brescia, con las violas encabezadas por Gasparo da Salò, y Cremona, con los violines representados por Andrea Amati. Este último es quien quizás pueda ser considerado el inventor del violín moderno, si debemos ceder semejante mérito a una única persona.
 Árbol «genealógico» de la escuela de lutería de Cremona. Fuente Wikimedia Commons
Árbol «genealógico» de la escuela de lutería de Cremona. Fuente Wikimedia CommonsCómo medir el carácter tonal del violín
La acústica musical puede modelar el carácter tonal de un violín midiendo distintos parámetros importantes en la caja de resonancia. La forma más completa de caracterizar la calidad de un instrumento es medir la movilidad de su caja al recibir vibraciones de las cuerdas a través del puente.
La movilidad de la caja se denomina también admitancia mecánica (inverso de la impedancia mecánica) que se define como el cociente entre la velocidad que se produce y la fuerza que se aplica en un sistema mecánico. Para medir la respuesta en frecuencia de la movilidad de un violín, debemos ejercer sobre la caja una fuerza oscilante barriendo todas las frecuencias audibles, y medir las velocidades con las que responde dicha caja para cada una de estas frecuencias.
Con un computador se puede emitir un ruido blanco a través de una bobina que induce oscilaciones mecánicas a todas las frecuencias en el cuerpo del violín. A su vez, puede medirse con un acelerómetro la respuesta mecánica de la caja a todas estas frecuencias, y efectuar un cálculo de la transformada de Fourier y un gráfico en el dominio de la frecuencia de todo el mapa de resonancias del instrumento [1].
 Método sencillo de medida del carácter tonal de un violín. Fuente: UPV/EHU, Dept Electricidad y Electrónica
Método sencillo de medida del carácter tonal de un violín. Fuente: UPV/EHU, Dept Electricidad y Electrónica
Las resonancias del cuerpo de los violines pueden caracterizar la acústica de todo tipo de instrumentos, incluyendo piezas históricas de gran calidad musical fabricadas hace siglos por los grandes lutieres [2].
 Ejemplo del espectro sonoro medido en un violín Fuente: Referencia [2]
Ejemplo del espectro sonoro medido en un violín Fuente: Referencia [2]
Las medidas acústicas de la caja de un violín pueden distinguir varias resonancias de esencial importancia para el sonido que podemos extraer del instrumento. La cavidad del aire de la caja vibra a una frecuencia propia que podemos excitar fácilmente soplando por una de las aberturas acústicas en forma de f del violín y escuchar la nota que surge de la otra f. Otras resonancias de la caja debidas a la madera, espesores, curvas, geometría y construcción nos permiten completar el espectro sonoro del instrumento, así como su firma y carácter tonal.
Referencias:
[1] Victor Etxebarria and Iratxe Riera (2002) Measuring the frequency response of musical instruments with a PC-based system. Catgut Acoustical Society Journal, vol 4, n. 6, (Series II), pp. 26-30.
[2] F Leccese, G Salvadori, G Bernardini and P Bernardini (2018) The bowed string instruments: acoustic characterization of unique pieces from the Italian lutherie. IOP Conf. Series: Materials Science and Engineering vol. 364 pp: 012022
Sobre el autor: Victor Etxebarria Ecenarro está diplomado como lutier por el Conservatorio Juan Crisóstomo de Arriaga (Bilbao) y es Catedrático de Ingeniería de Sistemas y Automática en la Universidad del País Vasco (UPV/EHU)
El artículo La caja de resonancia del violín se ha escrito en Cuaderno de Cultura Científica.
Naukas Bilbao 2022: La maravillosa labor investigadora de las moscas

¿Consideras que las moscas son criaturas “maravillosas”? ¿O que puedan tener un papel protagonista en la investigación contra enfermedades como el cáncer? ¿Alguna vez has llegado a reflexionar sobre la virginidad de estos insectos?
El investigador, doctor en Biología y profesor del departamento de Biología Celular de la Universidad de Sevilla Luis M. Escudero Cuadrado abordó estas cuestiones en su charla en Naukas Bilbao para responder que sí, que las tres son ciertas. ¿Por qué?
En primer lugar porque, aunque cueste trabajo creerlo, la mosca conocida como Drosophila melanogaster es muy parecida al ser humano. Tanto, que se utiliza para estudiar los procesos que llevan a la formación de nuestros órganos, hacer experimentos genéticos e intentar extraer conclusiones que resulten provechosas para la Humanidad. Para llevar a cabo estos experimentos los investigadores utilizan las moscas por varias razones: “Son pequeñas, manejables y tienen un ciclo de vida corto. En 10 días las moscas pasan del embrión a la larva y a la pupa; se produce la metamorfosis y tenemos nuevas moscas, y con una alta descendencia. Además, trabajar con ellas es barato”, explicó el científico.
Y es precisamente en este punto donde entra en juego la virtud de las hembras. Las moscas de este sexo tienen un órgano llamado espermateca que conserva un poco del esperma de cada uno de los machos con los que copula. Por eso, a la hora de garantizar que la información genética de las moscas no se vea alterada con el esperma de varios machos, es necesario que la hembra sea virgen e inducir la copulación en tubos de ensayo.
“Lo que hacemos es coger el tubo, dejar solo las pupas y esperar unas horas para que emerjan las nuevas moscas y tengamos así una guardería de vírgenes”, ilustró el investigador en lo que él mismo denominó “un curso completo de mamporrerismo de moscas en cuatro minutos”.
La finalidad de este “mamporrerismo” es encontrar genes que ayuden a descubrir aspectos que contribuyan a mejorar la vida del ser humano. ¿De qué manera? Luis M. Escudero se remontó a principios del siglo pasado, a los tiempos de Thomas H. Morgan, un genetista experto en investigación con moscas para responder a esta pregunta. Morgan quería resolver el enigma de la transmisión de la herencia genética entre generaciones cuando comenzó a cruzar una mosca con ojos blancos con otras con ojos rojos y se dio cuenta de que la información genética se hallaba en los cromosomas. Un hallazgo que le valió el Nobel de Medicina y Fisiología en 1933.
Morgan denominó white (blanco en inglés) a ese gen que daba la coloración blanca a los ojos de estos insectos, e inauguró la tradición de poner nombre a sus genes, hasta el punto de que hoy en día hay cientos de ellos. Por ejemplo, el gen tinman, que significa “hombre de hojalata”, es el que hace que se forme el corazón de forma correcta. Este gen tiene muchas similitudes con los genes humanos que participan en el proceso de formación del corazón.

Esta introducción permitió al investigador andaluz afirmar que la Drosophila es “maravillosa” ya que “las moscas han servido para investigar un montón de cosas que nos afectan, y para elaborar modelos de Alzheimer, Parkinson y cáncer”. ¿Cómo?
En concreto, el biólogo mencionó el ejemplo de un paciente con cáncer de colon a quien los tratamientos de cirugía, radioterapia y quimioterapia no le sirvieron para controlar la enfermedad e incluso comenzó a sufrir metástasis. Los investigadores identificaron los genes que estaban alterados en los tumores del paciente y crearon una serie de moscas con hasta ocho mutaciones diferentes que producían tumores muy parecidos a los suyos. Para intentar combatir estos tumores probaron en los insectos infinidad de combinaciones de compuestos hasta que dieron con una que conseguía que las moscas sobrevivieran. El resultado fue que después de 27 semanas de tratamiento el tamaño de las lesiones del paciente se redujo un 45%. Lamentablemente, el tratamiento se tuvo que suspender debido a un problema de efectos secundarios, pero abrió la puerta a nuevas investigaciones similares a las que se han desarrollado durante los últimos años.
Investigaciones como la que arrancó en La India hace 50 años con el descubrimiento de un gen, denominado wingless, que posibilita el crecimiento de las alas de una mosca han hecho que se avance muchísimo en la investigación biomédica. En aquella época la tasa de supervivencia en casos de cáncer de colon no superaba el 50%. “Ahora sabemos que los genes de esa familia están mutados en su gran mayoría de los tumores de colon”, explicó Escudero.
Los estudios de este tipo de genes en moscas, ratones y humanos han llevado a que hoy en día tengamos una tasa de supervivencia superior al 90% en este tipo de cáncer. El investigador concluyó su charla con un alegato optimista. “Trabajos como el que os acabo de comentar van a seguir aumentando esta estadística de cara a futuro. Seguro que sí”.
Si no ve correctamente el vídeo use este enlace.
Para saber más:
La inevitable ciencia de los bichos raros
Crónica de Roberto de la Calle / GUK
El artículo Naukas Bilbao 2022: La maravillosa labor investigadora de las moscas se ha escrito en Cuaderno de Cultura Científica.
Los usos terapéuticos de la psilocibina de los hongos alucinógenos
La psilocibina es un alcaloide que una vez ingerido en el cuerpo se convierte en psilocina, un compuesto alucinógeno responsable del efecto psicoactivo de ciertos hongos comestibles. La psilocibina se encuentra en fases avanzadas de ensayos clínicos dirigidos al tratamiento de diferentes patologías psiquiátricas, tales como la depresión o las adicciones. Investigadores del grupo de neuropsicofarmacología de la UPV/EHU han estudiado en profundidad el mecanismo de acción de la psilocibina en ratones.
 Psilocybe semilanceata. Fuente: Wikimedia Commons
Psilocybe semilanceata. Fuente: Wikimedia CommonsLa psilocibina se ha convertido en un fármaco potencialmente útil para varias enfermedades neuropsiquiátricas, presentando un inicio rápido de la actividad terapéutica. Sin embargo, los mecanismos responsables de tales efectos siguen siendo poco conocidos. El trabajo del grupo es relevante para comprender tanto el mecanismo de acción subyacente a los efectos terapéuticos como los potenciales efectos secundarios no deseados de esa sustancia psicodélica.
La psilocibina, naturalmente presente en algunas especies de hongos alucinógenos (hongos del género ‘Psilocybe’, entre otros), fue estudiada durante la década de los 60 para el tratamiento de diversos trastornos mentales, pero su uso y distribución quedaron prohibidos a partir de 1972. No obstante, en los últimos años, la comunidad científica ha retomado las investigaciones relacionadas con esa y otras sustancias de características similares, como el MDMA o el LSD.
Los ensayos clínicos desarrollados tanto en Europa como en América están dando resultados prometedores. “Esos estudios han sido el desencadenante para la descriminalización de la psilocibina y otros alucinógenos con potencial terapéutico en los Estados Unidos, lo que supone un avance para una futura aprobación para su uso clínico por las diferentes agencias reguladoras, principalmente la Food & Drug Administration (FDA) y la European Medicines Agency (EMA)”, explica Ines Erkizia, investigadora predoctoral del grupo y primera autora del artículo.
Los efectos agudos de la psilocibina y de su metabolito activo, psilocina, han sido ampliamente descritos tanto en entornos clínicos como por parte de usuarios en ambientes recreativos. Estos incluyen cambios en la percepción, como alucinaciones auditivas o visuales, y experiencias místicas o espirituales. Entre los efectos a largo plazo, los usuarios perciben cambios positivos en el humor y el estado de ánimo, lo cual podría suponer una mejora en la sintomatología de ciertas enfermedades psiquátricas. Los mecanismos que subyacen a esos efectos no son del todo conocidos, pero se han relacionado con incrementos de la plasticidad neuronal que parecen conllevar alteraciones en la conectividad de la corteza cerebral.
“Hemos confirmado un perfil farmacológico similar de psilocina en humanos y roedores -comenta la investigadora-. Además, se realizó un estudio farmacológico exhaustivo para identificar las dosis óptimas a utilizar en futuros estudios científicos de investigación básica y clínica. Nuestros hallazgos aportan datos valiosos sobre la implicación del sistema serotonérgico en los efectos de la psilocibina”, recalca Ines Erkizia.
Los resultados de esta investigación pueden proporcionar una nueva perspectiva sobre las dianas terapéuticas del fármaco para futuros estudios clínicos.
Para saber más:
Consumo de cannabis y desarrollo de esquizofrenia
Del metabolismo (y II)
Referencia:
I. Erkizia-Santamaría, R. Alles-Pascual, I. Horrillo, J.J. Meana, J.E. Ortega (2022) Serotonin 5-HT2A, 5-HT2C and 5-HT1A receptor involvement in the acute effects of psilocybin in mice. In vitro pharmacological profile and modulation of thermoregulation and head-twitch response Biomedicine & Pharmacotherapy doi: 10.1016/j.biopha.2022.113612
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Los usos terapéuticos de la psilocibina de los hongos alucinógenos se ha escrito en Cuaderno de Cultura Científica.
El piano que surgió de los restos de la guerra
Saltó a la fama gracias a The Doors y su sonido conquistó la música de finales de los 60 y principios de los 70. Se podía oír en todo tipo de música funk, rock y pop. Fue fundamental para el desarrollo del jazz-rock y de artistas como Miles Davis, Joe Zawinul, Chick Corea y Herbie Hancock. El piano Rhodes es ya un símbolo de toda una época. Lo que quizás no sabías es que en sus entrañas se encuentra la magia acústica del diapasón, y en sus orígenes, el horror de la guerra y bombarderos reciclados. Hoy te cuento su historia.
Viajemos hasta 1942. Europa se desangra bajo el peso de la Segunda Guerra Mundial, y han pasado pocos meses desde que Estados Unidos decidió enviar a sus soldados a la contienda. Entre las filas de estos recién llegados se encuentra un curioso personaje. Harold Rhodes ha sido reclutado para entrenarse como piloto de las fuerzas aéreas del ejército estadounidense1. Aunque todos le llaman oficial, él se define a sí mismo como profesor de piano —lo seguiría haciendo durante el resto de su vida—. Por eso, entre vuelo y vuelo, se dedica a dar clases de música a sus compañeros. Pronto, estas lecciones se vuelven tan populares, que el personal médico del ejército solicita su ayuda y Harold no se lo tiene que pensar dos veces. Equipado con su mejor arma, decide que su misión en medio del horror de la guerra será traer rehabilitación y consuelo a los soldados heridos, a través de la música.
Sin embargo, su tarea no era nada fácil. Para empezar, porque conseguir un piano para hacer musicoterapia de vanguardia no era precisamente una prioridad médica en medio de la Segunda Guerra Mundial —por lo que sea—. Pero además, muchos de los soldados que llegaban a sus manos se encontraban postrados en sus camas, sin posibilidad de moverse. Rhodes se vio forzado a inventar una nueva manera de impartir sus clases. En tiempos más felices, antes de la guerra, había puesto mucho empeño en enseñar a sus alumnos la mecánica de su instrumento, convencido de que entender el lenguaje de la música y cómo se produce el sonido era clave en su formación. Ahora, todo ese bagaje le ayudaría en su nuevo reto.
Rhodes se dispuso a crear un nuevo instrumento, un teclado portable y ligero, que los soldados pudieran tocar desde sus camillas, o sobre su regazo. Y ¿de dónde podía sacar el material necesario para construirlo? ¡De la propia guerra! Haciendo uso de su ingenio, decidió recurrir a una fuente insospechada de piezas de metal: aviones B-17 averiados. Las alas de estos bombarderos tenían unos tubos de aluminio que se podían cortar para crear láminas vibrantes de diferentes tonos. El “Xylette” —como llamó a su instrumento— tenía 29 teclas y era parecido a un xilófono, solo que con teclas. Una especie de piano de juguete. Y a pesar de ser bastante rudimentario, a los soldados les encantó. De hecho, el instrumento tuvo tanto éxito que Rhodes fue puesto a cargo del programa de rehabilitación de instrucción musical en todos los hospitales de la fuerza aérea. Se estima que el Xylette fue utilizado en hospitales de la Fuerza Aérea por miles de soldados.
 El prepiano Rhodes (1950) es uno de los más antiguos, un modelo muy anterior al famoso piano eléctrico Fender Rhodes (1965). Fuente: Wikimedia Commons
El prepiano Rhodes (1950) es uno de los más antiguos, un modelo muy anterior al famoso piano eléctrico Fender Rhodes (1965). Fuente: Wikimedia Commons
Después de la guerra, Rhodes siguió trabajando en su idea. Como buen profesor de piano, su objetivo era llevar su nuevo teclado a las aulas, para seguir enseñando música. Así que se le ocurrió amplificar su sonido electrónicamente y adaptarlo para estudiantes. El “Pre-Piano” contaba incluso con un asiento adjunto, como una especie de pupitre sonoro. Una década más tarde, Rhodes se asoció con Leo Fender para desarrollar y fabricar el piano Fender Rhodes que hoy conocemos. El primer modelo fue lanzado en 1959 y contaba solo con el registro más grave. Fue el modelo que popularizó The Doors. Raymond Manzarek, el teclista, lo utilizaba en sustitución del tradicional bajo eléctrico. Poco más tarde, salió al mercado el primer teclado completo de 73 notas: el Fender Rhodes Mk1.
¿Pero cómo funciona exactamente este piano eléctrico? Bien, el mecanismo no es muy diferente al de un piano real, solo que, en lugar de cuerdas, tiene unas piezas de metal que vibran a distinta frecuencia. Cuando el martillo las golpea, su vibración es capturada por un transductor que convierte su energía acústica en una señal eléctrica, como sucede en una guitarra eléctrica.
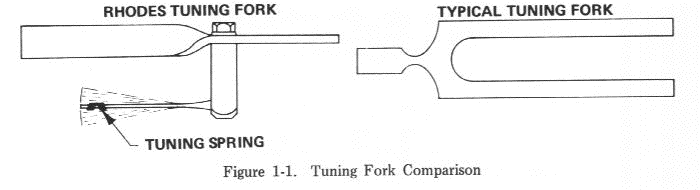
Pues bien, esas piezas de metal que sustituyen a las cuerdas son diapasones. ¡Sí, diapasones! Bueno, quizás un tipo de diapasón un tanto más asimétrico que el que solemos imaginar, pero instrumentos perfectamente equivalentes desde un punto de vista físico. En este caso, las patas de las varillas tienen distinta forma, masa y tamaño, pero son iguales en el tono. Y al igual que los diapasones, su sonido tiene propiedades especialmente interesantes para los músicos.
 Piano Rhodes sin la tapa de forma que las piezas de metal (diapasones) quedan visibles. Fuente: Wikimedia Commons
Piano Rhodes sin la tapa de forma que las piezas de metal (diapasones) quedan visibles. Fuente: Wikimedia CommonsDe hecho, el piano de Rhodes resultó revolucionario en su época. Por primera vez en la historia, los teclistas podían llevar su propio piano portátil de viaje. Bueno, todo lo “portátil” que puede ser un piano, entiéndase. Nadie les libraba de cargarlo en una camioneta cada noche. Pero gracias a las propiedades del diapasón, el Rhodes apenas se desafinaba. Y como alternativa era mucho mejor, que el piano destartalado de turno que pudieran encontrarse en los clubes donde tocaban.
Pronto este instrumento conquistó el mundo del rock y de la música. A mí me cuesta oír su sonido sin que me venga a la cabeza de inmediato The Doors. Pero muchos otros artistas recurrieron a este piano electrónico, desde Herbie Hancock a los Beatles o Michael Jackson. No está nada mal para un piano de juguete fabricado con aviones reciclados.
Referencia:
1Elaine Woo, 2001. “Harold B. Rhodes; Inventor of Electric Piano”. Los Angeles Times. Consultado el 1 de noviembre de 2022.
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo El piano que surgió de los restos de la guerra se ha escrito en Cuaderno de Cultura Científica.
¿Existen recorridos mágicos del caballo en el tablero de ajedrez?
Mis dos últimas entradas del Cuaderno de Cultura Científica han estado dedicadas a un problema clásico que relaciona matemáticas y ajedrez, el conocido problema del recorrido del caballo sobre el tablero de este juego. La primera de esas entradas, titulada El problema del recorrido del caballo en el tablero de ajedrez la dedicábamos a explicar el problema y a analizar la existencia de recorridos sobre tableros de ajedrez generales, no solo el clásico tablero cuadrado 8 x 8, sino tableros cuadrados o rectangulares de diferentes tamaños. Mientras que la segunda entrada, titulada El problema del recorrido del caballo en el tablero de ajedrez (II), se centraba en algunos métodos (algoritmos) históricos (de matemáticos como los franceses Abraham de Moivre (1667-1754) y Pierre Rémond de Montmort (1678-1719), o el suizo Leonhard Euler (1707-1783), entre otros) para construir dichos recorridos.
 Jaque mate (alrededor de 2010), del artista canadiense Paul Ygartua. Véase la obra en su página web, Imagen de su página web: Paul Ygartua
Jaque mate (alrededor de 2010), del artista canadiense Paul Ygartua. Véase la obra en su página web, Imagen de su página web: Paul YgartuaEn esta entrada, vamos a relacionar el rompecabezas del recorrido del caballo con la construcción de cuadrados mágicos, dos cuestiones que no tienen aparentemente ninguna conexión.
El problema del recorrido del caballoLo primero, como no puede ser de otra manera, es recordar el rompecabezas del que estamos hablando.
Problema del recorrido del caballo: Buscar un recorrido de la figura del caballo sobre el tablero de ajedrez (considerado este en un sentido general, es decir, tableros de diferentes formas y tamaños, principalmente cuadrados y rectangulares) que consista en mover esta pieza del juego, desde una casilla inicial, de forma sucesiva a través de todas las casillas del tablero, pasando una sola vez por cada una de ellas, y terminando en la casilla inicial (recorrido cerrado) o en otra casilla distinta (recorrido abierto).
Por ejemplo, en la siguiente imagen mostramos dos soluciones de este juego, una con un recorrido abierto y otra con un recorrido cerrado, que obtuvimos en la anterior entrada con la técnica de De Moivre y De Montmort.
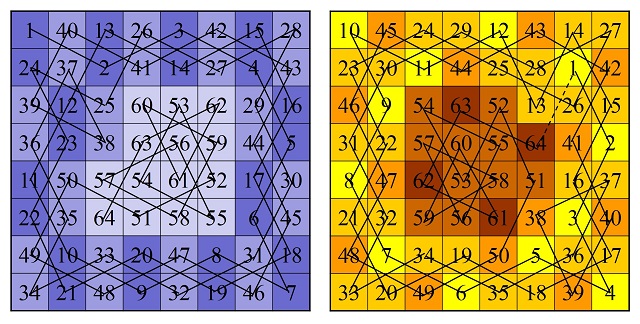 Recorridos abierto y cerrado obtenidos con el algoritmo de De Moivre-De Montmort
Recorridos abierto y cerrado obtenidos con el algoritmo de De Moivre-De Montmort
Además, recordemos que hemos numerado las casillas del tablero de ajedrez generalizado según el orden del recorrido del caballo, es decir, la casilla inicial esta numerada como 1, la siguiente sobre la que salta el caballo 2, después 3, y así hasta la casilla 64. De forma que, al resolver el problema del recorrido del caballo, hemos generado una retícula cuadrada con los números del 1 al 64, en general, del 1 al número de casillas del tablero.
Ya el matemático más prolífico de todos los tiempos, Leonhard Euler (1707-1783), que, como comentamos en la anterior entrada, fue el primero en realizar un análisis matemático riguroso del juego del recorrido del caballo en su artículo Solución a una cuestión ingeniosa que parece que no ha sido analizada (Memoria de la Academia de Ciencias de Berlín, escrito en 1759 y publicado en 1766), observó que los números pares e impares se distribuyen de forma alternada sobre el tablero de ajedrez. Si tenemos pintadas de blanco y negro las casillas del tablero con su típica distribución alternada, cada color alberga a todos los números pares o impares.
Los cuadrados mágicosLos cuadrados mágicos son unos objetos matemáticos que han cautivado a matemáticos y no matemáticos a lo largo de la historia. Se pueden encontrar, normalmente, en libros de divulgación de las matemáticas, de matemática recreativa o incluso de magia, pero también, como mostraremos hoy, en libros de ajedrez. Sobre ellos investigaron grandes matemáticos como el francés Pierre de Fermat (1607-1665) o Leonhard Euler, y hasta personalidades como el político, científico e inventor Benjamin Franklin (1706-1790), se atrevieron con ellos. Los cuadrados mágicos ya se conocían desde la antigüedad (quizás más allá del año 2.200 a.n.e.), y se les relacionaba con los planetas y con la alquimia, con la magia y la astrología, con la numerología, y también se utilizaban para sanar o como amuletos.
Pero vayamos con la definición de cuadrado mágico. Primero empecemos con un ejemplo, el cuadrado mágico más sencillo, que es el cuadrado mágico de orden 3. Se trata de un retículo cuadrado de tamaño 3 x 3, en el que se han colocado los números del 1 al 9, por ejemplo, como se muestra en la siguiente imagen.
 Cuadrado mágico de orden 3, conocido como Lo-Shu
Cuadrado mágico de orden 3, conocido como Lo-Shu
Como se puede observar la primera fila 4 – 9 – 2, la segunda fila 3 – 5 – 7 y la tercera 8 – 1 – 6 están formadas, cada una de ellas, por tres números cuya suma es la misma en los tres casos, en concreto, 15. Efectivamente, 4 + 9 + 2 = 3 + 5 + 7 = 8 + 1 + 6 = 15. Por otra parte, si sumamos los números de cada columna, suman de nuevo 15. La primera columna 4 + 3 + 8 = 15, la segunda 9 + 5 + 1 = 15 y la tercera 2 + 7 + 6 = 15. Más aún, la suma de los números de las dos diagonales principales suma de nuevo 15, como se comprueba fácilmente, 4 + 5 + 6 = 8 + 5 + 2 = 15. ¡Esto es exactamente un cuadrado mágico de orden 3!
Este cuadrado mágico 3 × 3, conocido como Lo-Shu, aparece por primera vez en uno de los cinco libros clásicos de la Antigua China, el I-Ching o Libro de las permutaciones (sobre el siglo 1.200 a.n.e), aunque una leyenda afirma que es mucho más antiguo, que fue visto por el emperador chino Yu, hacia el 2.200 a.n.e., en el caparazón de una gran tortuga. Sobre esta leyenda y algunas otras cuestiones relacionadas con los cuadrados mágicos las podéis leer en la serie de entradas del Cuaderno de Cultura Científica titulada Habibi y los cuadrados mágicos (primera parte, segunda parte y tercera parte).
En general, un cuadrado mágico de orden n (en el caso anterior, n = 3), es una distribución de los n2 primeros números (para orden 3, los 9 primeros números, 1, 2, 3, 4, 5, 6, 7, 8, 9), sobre las casillas de una retícula cuadrada n x n, (en el ejemplo anterior, 3 x 3), de forma que la suma de cada fila, cada columna y cada diagonal sea siempre la misma (para orden 3 es 15) y a ese número se le llama constante del cuadrado mágico.
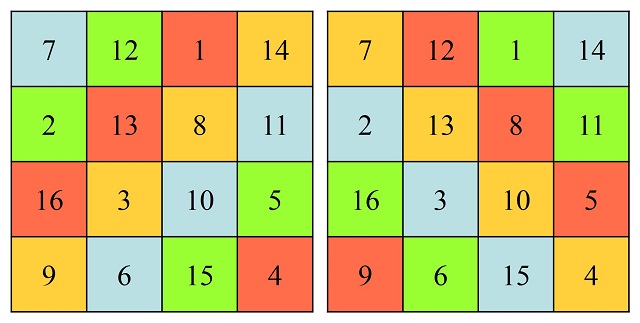
Un ejemplo de cuadrado mágico de orden 4 lo vemos en la siguiente imagen. En el mismo la suma de cada fila, cada columna y cada diagonal es 34.
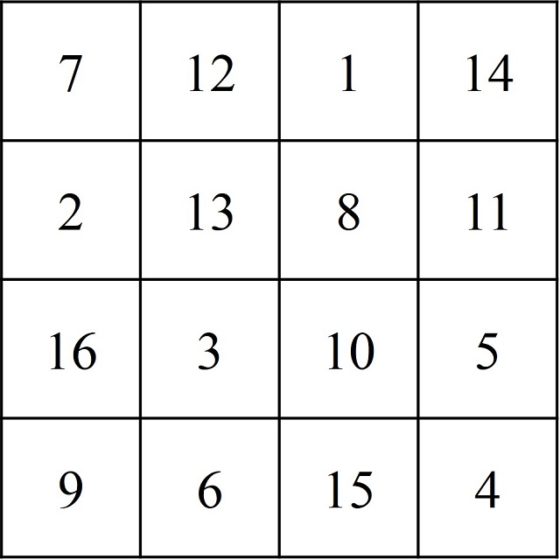 Cuadrado mágico de orden 4 que aparece en un pilar de un templo de Khajurado (India), y que es la primera representación gráfica de la que se tiene constancia en la que aparece un cuadrado mágico de orden 4
Cuadrado mágico de orden 4 que aparece en un pilar de un templo de Khajurado (India), y que es la primera representación gráfica de la que se tiene constancia en la que aparece un cuadrado mágico de orden 4Los cuadrados mágicos y el recorrido del caballo
Teniendo en cuenta que cada recorrido del caballo sobre el tablero de ajedrez genera una retícula de números, que en el caso de tableros cuadrados de tamaño n x n es una retícula cuadrada, es posible plantearse si esta podría ser un cuadrado mágico.
La primera persona que se planteó esta cuestión, que tengamos constancia de ello, sobre el tablero de ajedrez clásico fue William Beverly (no está clara la identidad de William Beverly, pero se cree que podría ser el pintor William Roxby Beverley (aprox. 1814-1889)) en el artículo On the Magic Square of the Knight’s March (Sobre el cuadrado mágico del camino del caballo), publicado en la revista The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science (vol. 33, no. 220, pp. 101–105, 1848). En el mismo presentaba el siguiente retículo cuadrado numérico generado por un recorrido abierto del caballo sobre el tablero de ajedrez.
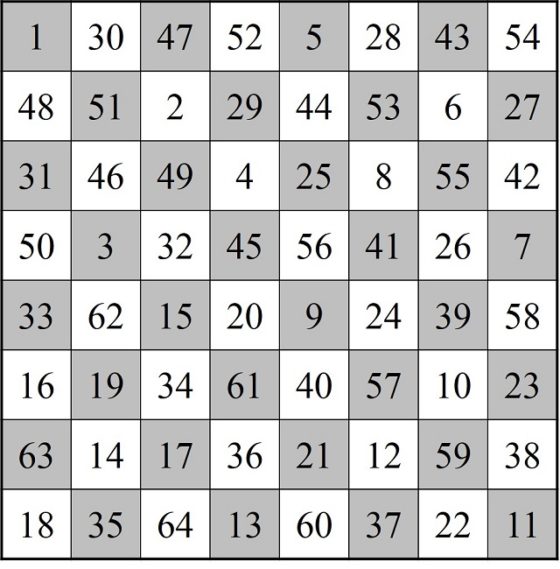 Recorrido abierto del caballo sobre el tablero de ajedrez, con curiosas propiedades numéricas, publicado por William Beverley en 1848
Recorrido abierto del caballo sobre el tablero de ajedrez, con curiosas propiedades numéricas, publicado por William Beverley en 1848
Este cuadrado numérico, en ocasiones erróneamente atribuido a Leonhard Euler, cumple la propiedad de que la suma de los números de cada fila y de cada columna es la misma, en concreto, 260. Es lo que se conoce como cuadrado semi-mágico de orden 8, ya que la suma de los números de las diagonales no es 260, sino 210 y 282.
La constante mágica para orden 8 es 260, como ocurre con el ejemplo de Beverley, ya que en general, la constante de un cuadrado semi-mágico de orden n es igual, como se puede deducir fácilmente, a:
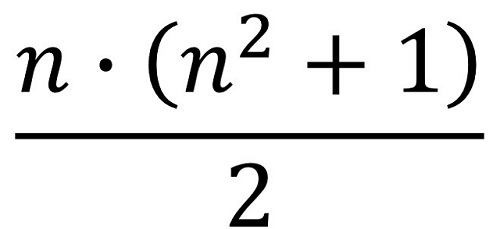
Una sencilla propiedad de los cuadrados semi-mágicos obtenidos mediante el recorrido del caballo es que el recorrido inverso, es decir, que empieza por el final y termina en el principio, también es un cuadrado semi-mágico. El propio William Beverley pone de manifiesto este hecho en su ejemplo, como se puede ver en su publicación (siguiente imagen).
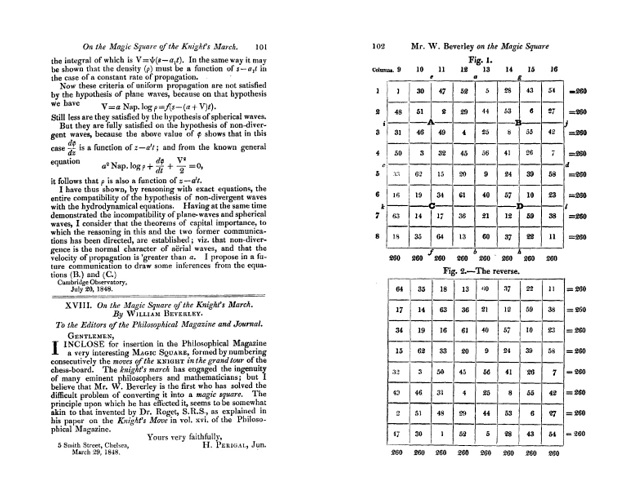 Las dos primeras páginas del artículo On the Magic Square of the Knight’s March, publicado en la revista The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, con la introducción del matemático amateur Henry Perigal, Junior (1801–1898) y el recorrido del caballo, y su reverso, cuyas filas y columnas suman 260
Las dos primeras páginas del artículo On the Magic Square of the Knight’s March, publicado en la revista The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, con la introducción del matemático amateur Henry Perigal, Junior (1801–1898) y el recorrido del caballo, y su reverso, cuyas filas y columnas suman 260
Aunque este cuadrado semi-mágico cumple algunas propiedades más (puede verse el artículo original de William Beverley), sigamos con el problema de la relación de los recorridos del caballo con los cuadrados mágicos.
El primer cuadrado semi-mágico generado por un recorrido cerrado del caballo se debe al húngaro Carl Wenzelides (tampoco está clara su identidad, según el matemático y experto en ciencias de la computación Donald Knuth (1938) sería un historiador, que además escribió sobre poesía y música, y vivió entre los años 1770 y 1852) y apareció en el artículo Bemerkungen über den Rösselsprung (Observaciones sobre el salto del caballo), publicado en 1849 en la revista de ajedrez Schachzeitung.
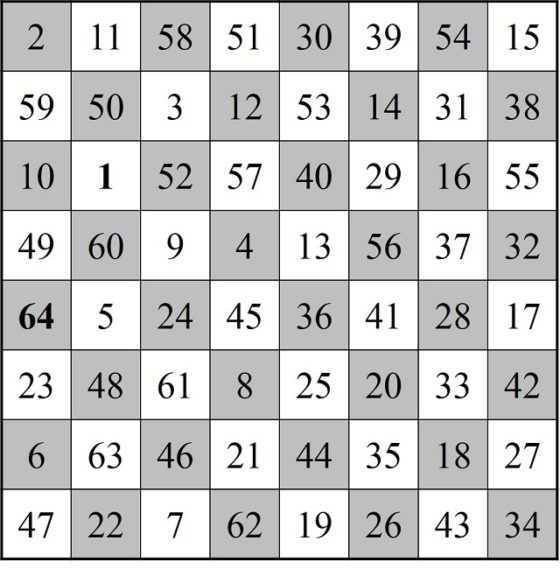 Cuadrado semi-mágico de Carl Wenzelides generado por un recorrido cerrado del caballo
Cuadrado semi-mágico de Carl Wenzelides generado por un recorrido cerrado del caballo
En este cuadrado numérico, las sumas de cada una de las diagonales no es 260, luego tampoco es un cuadrado mágico, pero cumple una curiosa propiedad, que la suma de los números de las dos diagonales es el doble de 260, 304 + 216 = 520.
En los siguientes años fueron apareciendo algunos ejemplos más de cuadrados semi-mágicos generados mediante recorridos del caballo sobre el tablero de ajedrez. Entre otros, el siguiente debido al jugador y teórico del ajedrez ruso-finlandés Carl Ferdinand Jaenisch (1813–1872), que aparecía en el artículo De la solution la plus parfaite du problème du cavalier (Sobre la solución más perfecta del problema del caballo), publicado en 1859 en la revista de ajedrez The Chess Monthly.
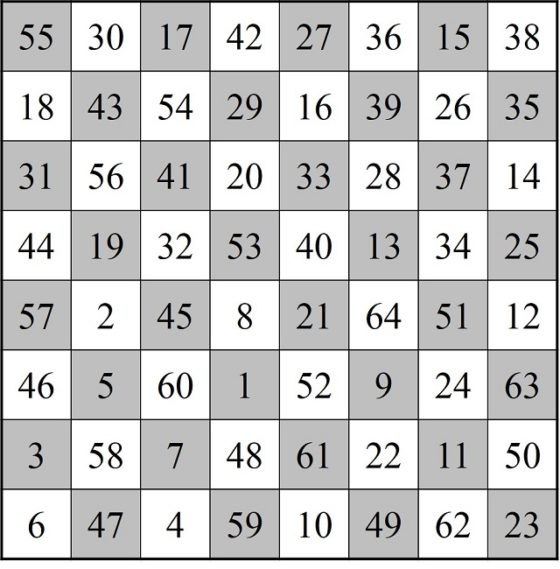
La perfección viene por dos motivos. El primero es que, si dibujamos, con segmentos, el camino realizado por el caballo, este tiene simetría rotacional (180 grados), como se observa en la imagen.
El otro motivo es que, aunque los números de las diagonales no son 260, sino 256 y 264, la suma da de nuevo 520, el doble de 260, pero además se verifica otra curiosa propiedad relacionada con las diagonales no principales, las diagonales fragmentadas. Para explicarlo mejor, vayamos de nuevo al ejemplo del cuadrado mágico de orden 4 que habíamos mostrado anteriormente, cuyas filas, columnas y diagonales principales sumaban 34. Pero, además, ese cuadrado mágico, cumple otra propiedad, que las diagonales fragmentadas descendentes y ascendentes (que mostramos con el mismo color en la siguiente imagen, también suman 34).
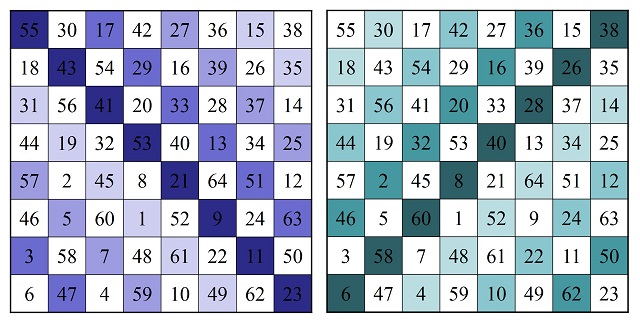
En el cuadrado semi-mágico de Jaenisch ocurre algo similar, pero solo parcialmente. Los números de la diagonal principal descendente (azul oscuro en la siguiente imagen) suman 256, así como las diagonales fragmentadas paralelas (diferentes tonos de azul). Por otra parte, la suma de la diagonal principal ascendente (verde oscuro en la siguiente imagen) es 264, así como las diagonales fragmentadas paralelas (diferentes tonos de verde).
Siguieron encontrándose ejemplos de cuadrados semi-mágicos obtenidos mediante el recorrido del caballo (recorridos semi-mágicos). En 1951, el pedagogo, inspector de educación e historiador del ajedrez británico Harold J. R. Murray (1868 – 1955), autor del libro Historia del ajedrez, escribió la monografía The Magic Knight’s Tours. A Mathematical Recreation (Los recorridos del caballo mágicos, una recreación matemática), que recogía los 126 semi-mágicos obtenidos mediante recorridos del caballo, 59 de ellos cerrados, que se conocían hasta ese momento. Pero esta monografía se quedó en el cajón, por lo que el listado de estos cuadrados semi-mágicos no fue publicado hasta 1986. Apareció en el artículo Catalogue of 8 x 8 magic knight’s tours (Chessics 26, pp. 122-128), del matemático y editor británico George P. Jelliss, quien es el autor de una página web muy exhaustiva sobre el problema del recorrido del caballo.
A raíz de la publicación de este catálogo de 126 cuadrados semi-mágicos, se descubrió que aún había más recorridos semi-mágicos. Entre 1987 y 1988, el aficionado a las matemáticas británico Thomas W. Marlow (1927-2011) encontró, utilizando métodos computacionales, 5 cuadrados semi-mágicos más. A los que se les añadió 2 más, en 2003, por parte del australiano Timothy S. Roberts, profesor del Departamento de Informática y Comunicación de la Central Queensland University.
Sin embargo, ninguno de ellos era un cuadrado mágico, por lo que aún seguía abierto, tras más de 150 años, el problema de si existían recorridos (abiertos o cerrados) del caballo en el tablero de ajedrez que generaran un cuadrado mágico.
Finalmente, Hugues Mackay (Canada), Jean-Charles Meyrignac (Francia) y Günther Stertenbrink (Alemania) decidieron unir sus fuerzas y desarrollar un software que analizara computacionalmente todos los posibles recorridos del caballo en el tablero 8 x 8. El resultado, obtenido en 2003, fue que:
¡no hay recorridos del caballo que generen cuadrados mágicos!
Además, obtuvieron 7 nuevos cuadrados semi-mágicos, tres abiertos y cuatro cerrados, que no se habían obtenido antes. De esta forma, se cerró el catálogo de recorridos del caballo que generan cuadrados semi-mágicos, con una extensión de 140, de los cuales 63 son cerrados.
 A. O. Magic Square Face #B2 (2019), del artista alemán Thomas Zipp (1966), que forma parte de la instalación The Church of the Magic Square (2020), para la galería Blank Projects [blankprojects.com] de Sudáfrica
A. O. Magic Square Face #B2 (2019), del artista alemán Thomas Zipp (1966), que forma parte de la instalación The Church of the Magic Square (2020), para la galería Blank Projects [blankprojects.com] de Sudáfrica
Los recorridos del caballo mágicos en tableros de cualquier tamaño
Puesto que se pueden obtener retículos cuadrados numéricos para recorridos del caballo sobre tableros cuadrados de cualquier tamaño n x n, es lógico preguntarse si sería posible construir cuadrados mágicos con recorridos del caballo para grados distintos de 8.
La primera reflexión que podemos realizar es que no van a existir tales cuadrados mágicos, ni semi-mágicos, para ordenes n impares. El motivo es muy simple.
Si tomamos el tablero de ajedrez cuadrado, de tamaño n x n, y pintamos sus casillas de blanco y negro, de forma alterna, como es habitual, el caballo en su salto va a pasar de una casilla negra a una blanca, y viceversa, pero cuando contamos las casillas del recorrido después de un número par viene uno impar, y viceversa, luego todos los números pares estarán en las casillas de un mismo color y los impares en las casillas del otro, como podéis comprobar además en los ejemplos mostrados más arriba para el tablero 8 x 8. Por lo tanto, si nuestro tablero n x n es tal que n es impar (n = 2k + 1), tendremos que dos columnas cualesquiera, respectivamente filas, contiguas tendrán una de ellas k casillas negras y k + 1 blancas, mientras que la otra tendrá k casillas blancas y k + 1 negras. Como la paridad está asociada al color, entonces la suma de los números de una de esas dos columnas (resp. filas) será par, mientras que la suma de la otra será impar. Por lo tanto, no pueden coincidir.
¡No existen recorridos (semi-)mágicos en los tableros de tamaño n x n, con n impar!
 Magic Square of Five (Twins) (2020), del artista alemán Thomas Zipp (1966), que forma parte de la instalación The Church of the Magic Square (2020), para la galería Blank Projects [blankprojects.com] de Sudáfrica
Magic Square of Five (Twins) (2020), del artista alemán Thomas Zipp (1966), que forma parte de la instalación The Church of the Magic Square (2020), para la galería Blank Projects [blankprojects.com] de Sudáfrica
La cuestión es ahora qué pasa para el resto de los tamaños de los tableros, para aquellos tales que n es par. Se pueden considerar dos tipos de tamaños distintos, aquellos para los que n = 4k y aquellos para los que n = 4k + 2, que son todos. Los hemos separado así porque G. P. Jelliss demostró, en 2003, que no existen recorridos del caballo mágicos para tableros n x n, con n = 4k + 2. Por lo tanto, solo hay que considerar aquellos tamaños para los que n = 4 k (siendo k mayor que 1, ya que recordemos que no existen recorridos sobre el tablero 4 x 4, como se comentó en la entrada El problema del recorrido del caballo en el tablero de ajedrez).
¡No existen recorridos (semi-)mágicos en los tableros de tamaño n x n, con n = 4k + 2!
A pesar de todos los resultados negativos que hemos mostrado sobre la obtención de recorridos del caballo que generen cuadrados mágicos, sí existen resultados positivos. El orden más pequeño para el que pueden existir recorridos mágicos es n = 12 (cuya constante es 870) y en 2003, el jugador de ajedrez y aficionado a las matemáticas Awani Kumar encontró finalmente cuatro recorridos abiertos del caballo que generan un cuadrado mágico (véase uno de ellos en la siguiente imagen).
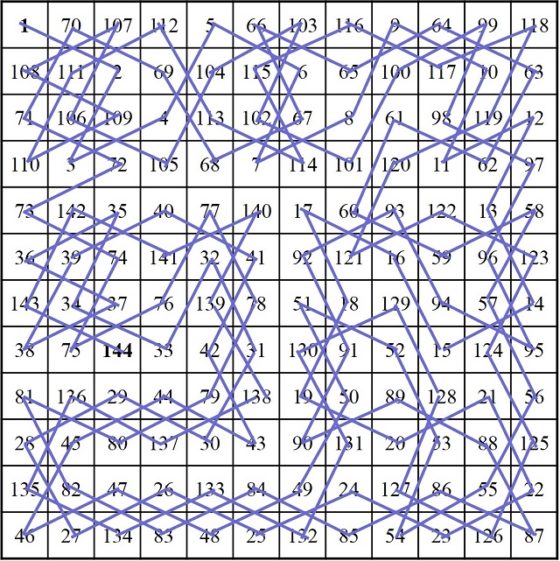 Recorrido mágico abierto del tablero 12 x 12, obtenido por Awani Kumar en 2003
Recorrido mágico abierto del tablero 12 x 12, obtenido por Awani Kumar en 2003
Aunque sigue abierto el problema de encontrar recorridos mágicos cerrados sobre el tablero de tamaño 12 x 12.
Curiosamente para el siguiente tamaño posible, 16 x 16 (cuya constante es 2056), se encontraron antes ejemplos. Además, algunos de ellos son de recorridos cerrados. En 1956, utilizando un método desarrollo por Harold J. R. Murray, Helge Emanuel de Vasa (de quien no tengo ninguna referencia) y el empleado de banca aficionado a las matemáticas y al ajedrez británico Theophilus H. Willcocks (1912-2014), obtuvieron los primeros ejemplos de recorridos mágicos para el tablero 16 x 16. Los dos ejemplos de H. E. de Vasa, que son recorridos cerrados, se publicaron en 1962, en el libro Les secrets du cavalier, le problème d’Euler (Los secretos del caballo, el problema de Euler) de G. D’Hooghe, y en 1968, en un artículo de T. H. Willcocks en Recreational Mathematics Magazine. El ejemplo de T. H. Willcocks, que es un recorrido abierto, fue publicado en 1968 en un artículo en Journal of Recreational Mathematics.
 Recorrido mágico cerrado sobre el tablero 16 x 16, obtenido por H. E. de Vasa en 1956 y publicado en 1968. Imagen de la Concise Encyclopedia of Mathematics de Eric W. Weisstein
Recorrido mágico cerrado sobre el tablero 16 x 16, obtenido por H. E. de Vasa en 1956 y publicado en 1968. Imagen de la Concise Encyclopedia of Mathematics de Eric W. Weisstein
Se han obtenido recorridos mágicos para tableros de tamaños 20 x 20, 24 x 24, 32 x 32 y 48 x 48, como puede verse en las notas sobre el recorrido del caballo de George Jelliss: Knight’s Tour Notes.
 Super-ajedrez (1937), del artista suizo-alemán Paul Klee (1879-1940)
Super-ajedrez (1937), del artista suizo-alemán Paul Klee (1879-1940)
Bibliografía:
1.- Raúl Ibáñez, Del ajedrez a los grafos, la seriedad matemática de los juegos, El mundo es matemático, RBA, 2015.
2.- Édouard Lucas, Recreaciones Matemáticas, vol. 1 – 4, Nivola, 2007, 2008.
3.- Miodrag S. Petrovic, Famous Puzzles of Great Mathematicians, AMS, 2009.
4.- Harold J. R. Murray, A History of Chess (Historia del ajedrez), Oxford University Press, 1913.
5.- W. W. Rouse Ball, H. S. M. Coxeter, Mathematical Recreations and Essays, Dover Publications, 1987 (originalmente publicada por W. W. R. Ball en 1892 –la versión original puede encontrarse en el Proyecto Gutenberg – y extendida por el geómetra H. S. M. Coxeter en 1974)
6.- John J. Watkins, Across the Board: The Mathematics of Chessboard Problems, Princeton University Press, 2004.
7.- John D. Beasley, Magic Knight`s Tours, The College Mathematical Journal, vol. 43, no. 1, pp. 72 – 75, 2012.
8.- George Jelliss, Knight’s Tour Notes, 2019.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo ¿Existen recorridos mágicos del caballo en el tablero de ajedrez? se ha escrito en Cuaderno de Cultura Científica.
Einstein y Franklin D. Roosevelt
El ya mundialmente famoso Albert Einstein emigró a Estados Unidos en el otoño de 1933. Poco después, él y su mujer fueron invitados a cenar por el presidente Roosevelt. El 24 de enero de 1934 tuvo lugar la cena, y el matrimonio Einstein pasó la noche la Casa Blanca. Años después, la relación establecida aquella velada animó a Einstein a escribir una carta a Roosevelt que contribuiría a cambiar el curso de la historia.
 La respuesta de Roosevelt a la carta de Einstein. Fuente: Wikimedia Commons
La respuesta de Roosevelt a la carta de Einstein. Fuente: Wikimedia CommonsLa invitación inicial a cenar en la Casa Blanca vino tras la insistencia del rabino Stephen Wise. Alarmado por las políticas racistas de Alemania y ante lo que él creía inacción de Roosevelt, Wise usó sus contactos para convencer a un asesor del presidente para que el presidente recibiera a Albert Einstein, argumentando que, de no hacerlo, sería un desprecio hacia los judíos. La esperanza de Wise era que Einstein pudiera explicarle de primera mano la situación que estaba viviendo su pueblo en Alemania. La invitación fue enviada por la Casa Blanca sólo dos semanas después de la llegada de Einstein; sin embargo, esa primera invitación fue, increíblemente, rechazada.
En 1930 se había fundado el Instituto de Estudios Avanzados en Princeton, del que se había hecho cargo su primer director, Abraham Flexner. Contratar a Einstein había sido una maniobra genial (y de suerte) por parte de Flexner, y una que algunas veces el mismo Flexner valoró con satisfacción y otras con arrepentimiento. Einstein, el científico más famoso del mundo, le proporcionó al recién fundado Instituto prestigio inmediato, esta era la parte buena para Flexner. Pero Einstein era también el judío vivo más famoso, y esto era malo o, al menos, preocupante para Flexner, él mismo judío. Cuando Albert y Elsa Einstein llegaron al puerto de Nueva York el 17 de octubre de 1933, recibieron una nota de Flexner antes de desembarcar. Decía: “Hay bandas organizadas de nazis irresponsables en este país […] su seguridad en Estados Unidos depende del silencio y de abstenerse de aparecer en actos públicos”. Flexner había sido advertido por el subsecretario de estado Phillipps de que Einstein debía mantener un perfil bajo, pero Einstein sospechaba que lo que estaba en juego no era tanto su seguridad como la tranquilidad de Flexner.
Flexner abría todo el correo que llegaba al Instituto para Einstein. Fue Flexner el que telefoneó al secretario de prensa de la Casa Blanca para declinar la invitación alegando que el profesor Einstein había venido para investigar, no para dedicarse a la política. Cuando Einstein se enteró, accidentalmente, de lo que había pasado, a la vergüenza que sintió por lo que el presidente de la nación que le acogía podía haber pensado, se unió la furia contra Flexner. Finalmente, se decidió a escribir a Eleanor Roosevelt, explicando lo sucedido, y poco después llegaba una segunda invitación.
El encuentro entre los Einstein y los Roosevelt es evidente que fue agradable. Sin embargo, ninguna de las partes comentaría demasiado qué había sucedido o de qué se había hablado. Eleanor Roosevelt escribiría a una amiga: “los Einstein llegaron […] y son únicos, tan alemanes y tan sencillos, con muchas sabias y delicadas cualidades alemanas”. Parece ser, por un comentario posterior que habría hecho Elsa, que Roosevelt propuso a Einstein que aceptara una ciudadanía honorífica, tal y como proponían dos miembros del Congreso, pero Einstein habría declinado el trato especial. Einstein sí parece que llegó a conectar a nivel personal con Roosevelt pues, según su amiga Frieda Bucky, habría dicho: “Lamento que Roosevelt sea presidente, de otro modo le visitaría a menudo”.
Si bien este encuentro no tuvo demasiadas consecuencias, el siguiente contacto de Einstein con Roosevelt puso al físico a la vanguardia de la era atómica. Los descubrimientos realizados en 1938 tenían a los físicos alborotados con las posibilidades que podía tener el estudio del uranio. Algunos comentarios de científicos alemanes a sus colegas americanos sobre las nuevas técnicas para romper átomos de uranio, y emplear la enorme energía que se liberaría, alarmaban a los que estaban preocupados con la posibilidad de que la Alemania de Hitler consiguiese una ventaja tecnológica de ese calibre, con usos militares tan evidentes. Siendo conocedor de estos nuevos desarrollos y temeroso de la destructividad de la Alemania nacionalsocialista, Einstein firmó el 2 de agosto de 1939, un mes antes de la invasión de Polonia, una de las cartas más famosas de la historia [se puede leer aquí]. Escrita en su mayor parte por Leó Szilárd, con la colaboración de Edward Teller y Eugene Wigner, en ella Einstein alertaba a Roosevelt del peligro y lo animaba a actuar primero, proveyendo fondos gubernamentales para la investigación. Si bien la carta no llevó a la acción inmediata, ciertamente fue la primera vez que Roosevelt fue consciente de lo que la nueva física podía significar para el desarrollo armamentístico. Roosevelt respondió el 19 de octubre.
Años después, en 1942, con Estados Unidos en guerra tras el ataque japonés a Pearl Harbour en diciembre de 1941, se puso en marcha el proyecto Manhattan, que terminaría con la construcción y detonación de la primera bomba atómica. Aquella carta fue la única contribución, indirecta, al proyecto por parte de Einstein. Su pacifismo y sus “sentimientos filocomunistas” impidieron que el F.B.I. emitiese la autorización para que se le invitase a participar plenamente. Pero esta es otra historia.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Una versión anterior de este artículo se publicó en Experientia Docet el 16 de mayo de 2010.
El artículo Einstein y Franklin D. Roosevelt se ha escrito en Cuaderno de Cultura Científica.
¿Cuándo acabó el vulcanismo lunar?
A pesar de que la Luna es nuestro vecino planetario más cercano, todavía nos quedan muchísimas dudas por resolver sobre su evolución a nivel geológico y cuál ha sido el grado de actividad geológica a nivel interno, incluyendo el vulcanismo lunar, que ha mantenido a lo largo del tiempo. Conocer estos detalles nos ayudaría a hacer nuevos modelos sobre la estructura y composición del interior de nuestro satélite y a comprender mejor su historia.
Para poder resolver todas estas dudas, tenemos que hacer uso de distintas técnicas: desde las observaciones de satélite que nos permiten conocer a grandes rasgos las edades de las unidades rocosas de la superficie lunar a través de las imágenes, a la instalación de sismómetros en la superficie lunar que nos permitan, mediante el cambio en las propiedades de las ondas sísmicas, conocer mejor las distintas capas que conforman su estructura interna.
No podemos olvidar que también necesitamos analizar rocas lunares en nuestros laboratorios, que a través de las técnicas modernas de datación y análisis nos pueden aportar una gran cantidad de información. Disponemos de una gran cantidad de rocas lunares traídas en su mayoría durante la década de los 60 y 70 por misiones como las norteamericanas Apollo o las soviéticas Luna.
 Imagen oblicua de un posible volcán en Oceanus Procellarum. Cortesía de NASA/GSFC/Arizona State University.
Imagen oblicua de un posible volcán en Oceanus Procellarum. Cortesía de NASA/GSFC/Arizona State University.La gran cantidad de muestras retornadas arrojan una edad cercana o superior a los 3000 millones de años, actividad concentrada especialmente entre los 3800 y los 3100 millones de años, lo que hacía a los científicos pensar que la Luna había perdido una gran parte -si no toda- de su actividad volcánica hace muchísimo tiempo.
Cuatro décadas -y algunos años después- de la última misión de retorno de muestras lunares, el 16 de diciembre de 2020 llegaban a la Tierra algo más de un kilo y setecientos gramos de nuevos materiales rocosos traídos por la sonda de la agencia espacial china Chang’e 5 que son los responsables de empezar a cambiar nuestra visión sobre la edad del vulcanismo lunar.
La Chang’e 5 aterrizó en Oceanus Procellarum, uno de los grandes mares lunares formados por la acumulación de lava fruto de erupciones continuadas en la superficie lunar. Precisamente en este lugar los científicos habían observado la existencia de formas volcánicas más jóvenes -en apariencia- de lo esperado.
 Lugar de aterrizaje de la Chang’e 5. Cortesía de NASA/GSFC/Arizona State University.
Lugar de aterrizaje de la Chang’e 5. Cortesía de NASA/GSFC/Arizona State University.¿Cómo podemos calcular aproximadamente la edad de las superficies planetarias? Pues lo hacemos a través de las imágenes: Cuanto más tiempo permanece una superficie expuesta a la colisión de otros cuerpos, más cráteres acumulará y, por lo tanto, más antigua será. Hoy día, mediante las técnicas de contaje de cráteres, se puede calcular una edad aproximada.
Pero también los impactos más pequeños y otros procesos pueden ir erosionando su forma original, haciendo que vaya difuminándose o suavizándose con el tiempo, algo parecido a como ocurre en nuestro planeta con los procesos atmosféricos.
¿Qué mecanismos podrían haber alimentado un vulcanismo que aparentemente era más tardío -y reciente- en la Luna? Al principio, los científicos se preguntaron si la presencia de elementos radioactivos -que al desintegrarse generan calor- era la responsable de esta anomalía, pero las muestras tomadas por la Chang’e 5 mostraban una cantidad de estos muy inferior a la esperada como para que fuese suficiente para generar este calor adicional capaz de provocar la fusión de las rocas y la formación de magmas.
Otra de las posibilidades era que las rocas tuviesen un mayor contenido en agua, lo que hubiese permitido bajar la temperatura de fusión y, por lo tanto, facilitar la formación de los magmas, pero tampoco era así.
Entonces, ¿qué fenómenos podrían estar ocasionando estos episodios de vulcanismo más reciente? Los autores de un nuevo estudio sugieren que la clave se encuentra en la mineralogía de las rocas, ya que han encontrado minerales ricos en calcio y titanio como los clinopiroxenos y la ilmenita.
 Fotografía de un basalto con ilmenita traído por la misión Apollo XVII. Cortesía de JSC/NASA.
Fotografía de un basalto con ilmenita traído por la misión Apollo XVII. Cortesía de JSC/NASA.Esta asociación de minerales se habría empezado a formar poco después del origen de la Luna, pero habrían continuado formándose y acumulándose durante la fase de enfriamiento gradual del satélite, probablemente en la base de la corteza. Debido a su mayor densidad -más que la del manto- habrían ido hundiéndose gradualmente hacia el núcleo, bajando la temperatura de fusión del manto, promoviendo su circulación, y permitiendo que el vulcanismo continuase hasta hace unos 2.000 millones de años.
Los autores, además, concluyen que el magma responsable de la formación de estas rocas apareció a unas profundidades similares a las que lo hizo el que dio lugar a las rocas que trajeron los astronautas de las misiones Apollo, pero que aproximadamente tenía una temperatura de unos 80 °C menos, por lo que además se puede observar como ha existido un enfriamiento lento y gradual del manto en los mil millones de años que separan las muestras traídas por las misiones Apollo y la Chang’e 5.
Sin duda, este estudio abre la posibilidad de crear nuevos modelos geoquímicos y geodinámicos que nos permitirán conocer un poco mejor la historia de nuestro satélite, pero también a decidir que lugares pueden ser los más interesantes de cara a traer nuevas muestras que puedan ayudarnos a desvelar los secretos del vulcanismo lunar.
Bibliografía:
Li, Q.-L., Zhou, Q., Liu, Y., Xiao, Z., Lin, Y., Li, J.-H., Ma, H.-X., Tang, G.-Q., Guo, S., Tang, X., Yuan, J.-Y., Li, J., Wu, F.-Y., Ouyang, Z., Li, C., & Li, X.-H. (2021). Two-billion-year-old volcanism on the Moon from chang’e-5 basalts. Nature, 600 (7887), 54–58. doi: 10.1038/s41586-021-04100-2
Su, B., Yuan, J., Chen, Y., Yang, W., Mitchell, R. N., Hui, H., Wang, H., Tian, H., Li, X.-H., & Wu, F.-Y. (2022). Fusible mantle cumulates trigger young mare volcanism on the Cooling Moon. Science Advances, 8 (42). doi: 10.1126/sciadv.abn2103
Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.
El artículo ¿Cuándo acabó el vulcanismo lunar? se ha escrito en Cuaderno de Cultura Científica.
La gota y la fruta
 Foto: Naveed Pervaiz / Unsplash
Foto: Naveed Pervaiz / UnsplashSi le hacen análisis de sangre con frecuencia, es posible que recuerde cuál suele ser su concentración de ácido úrico. No es aconsejable que tenga usted más de 7 mg por decilitro (mg/dL); los valores normales se encuentran entre 3,6 y 6,5 mg/dL y entre 2,5 y 6,5 mg/dL, en hombres y mujeres respectivamente. El ácido úrico es muy insoluble, por lo que tiene la mala costumbre de formar cristales y acumularse en lugares donde puede hacer mucho daño.
Lo que quizás no sepa es que la mayoría de los mamíferos tienen concentraciones de ácido úrico mucho más bajas que las nuestras, entre 1 y 2 mg/dL. No se trata de una excepción exclusivamente humana. El fenómeno es común a dos familias de primates, Hylobatidae (gibones) y Hominidae (grandes simios), esto es, orangutanes, gorilas, chimpancés, bonobos y seres humanos. Todos nosotros carecemos de uricasa, la enzima que permite que se degrade el ácido úrico a sustancias más solubles, que son después eliminadas en la orina.
Ya hace unos 60 Ma (millones de años), cuando los primates divergieron del resto de mamíferos, se empezaron a producir cambios en la uricasa que provocaron una pérdida progresiva de su capacidad catalítica. Pero para las dos familias antedichas las cosas cambiaron de forma mucho más drástica hace cerca de 20 Ma. Desde entonces, en los dos linajes -gibones, por un lado, y grandes simios, por el otro- y de forma paralela, se ha producido lo que, en jerga genética, se denomina una pseudogenización. En otras palabras: el gen del que depende la producción de uricasa está averiado, no produce la enzima y, como consecuencia de ello, nuestros niveles de úrico en sangre son muy altos, entre 3 y 10 veces más que los de los demás mamíferos.
Lo sorprendente es que los cambios que averiaron el gen de la uricasa se extendieran y hayan perdurado en el tiempo. Si los efectos de la pseudogenización, por no limitar las posibilidades de dejar descendencia a los individuos afectados, fuesen simplemente neutros, podría ocurrir que hubiese individuos con el gen averiado y otros con el gen funcional. Pero si todos los individuos de las especies afectadas carecen de la capacidad para degradar ácido úrico, es posible que de ello se derive alguna ventaja.
Hay evidencias empíricas, observacionales y experimentales, de que el ácido úrico facilita la conversión de la fructosa -el azúcar característico de la fruta- en grasas. Esto es una mala noticia para quienes tenemos alto el ácido úrico y comida abundante a diario. Pero quizás sea buena para quienes tienen acceso a abundante fruta en ciertos periodos del año, pero sufren privación durante largos periodos de tiempo, probablemente en invierno.
Cabe especular, por tanto, con la posibilidad de que hace entre 15 y 20 Ma, al comienzo del Mioceno, cuando se enfrió el planeta, el entorno en el que vivía el ancestro común de los grandes simios, y también el de los gibones, se hiciese más estacional de lo que era, con inviernos más severos. De ese modo, los frutos, uno de los principales sustentos de nuestros antepasados, pudieron desaparecer o escasear mucho durante el invierno, de manera que habría resultado de gran valor contar con un mecanismo mediante el que la fruta disponible en periodos de abundancia pudiese transformarse en reservas de energía que ayudasen a superar el invierno hasta la llegada de la siguiente estación de bonanza.
Si tiene el úrico alto o, incluso, padece de episodios de gota, esta hipótesis seguramente no le dará ningún consuelo, pero al menos le ayudará a entender mejor la causa última de su infortunio.
Para saber más:
Un gen ahorrador
El caso de la dieta de los esquimales
Fuentes:
Richard J. Johnson, Peter Andrews (2010): Fructose, Uricase, and the Back-to-Africa Hypothesis, Evolutionary Anthropology 19:250–257.
James T. Kratzer et al. (2014): Evolutionary history and metabolic insights of ancient mammalian uricases. PNAS 111 (10) 3763-3768. doi: 10.1073/pnas.1320393111
El artículo La gota y la fruta se ha escrito en Cuaderno de Cultura Científica.
Naukas Bilbao 2022: La señora de los anillos

Son fascinantes, relativamente desconocidos y rodean a más de cuatro planetas, aunque también visten a los llamados “enanos” y a los “centauros”. Son los extraordinarios anillos del Sistema Solar -y más allá-, formaciones que hasta hace poco creíamos formadas de partículas muy finas y de las que cada día conocemos más detalles.
La astrónoma y doctora en Física de la UPV-EHU Naiara Barrado-Izagirre participó en la pasada edición de Naukas Bilbao para ofrecer datos significativos, aportar imágenes inéditas sobre estas fantásticas y enigmáticas formaciones, y sobre todo, para responder a muchas dudas sobre este universo. Su exposición arrancó con el que ella misma denominó “el señor de los anillos” del Sistema Solar, Saturno, un planeta plagado de curiosidades. Sus siete anillos “no siempre estuvieron ahí”, sino que fue la misión Cassini la que descubrió que estas formaciones eran coetáneas de los dinosaurios en la tierra, es decir, que se formaron hace alrededor de 100 millones de años.
Tras esta presentación, la astrónoma respondió a dos cuestiones: ¿De qué están compuestos estos siete gigantescos anillos? Y ¿Son formaciones gaseosas, tal y como la propia investigadora sospechaba? Pues no: Naiara Barrado-Izagirre admitió que a pesar de lo que ella misma creía estas formaciones están compuestas de trozos de hielo de diferentes tamaños, que pueden oscilar entre las dimensiones de un autobús y de una mota de polvo.
Y continuó: ¿Cómo se formaron? La experta recordó que un día antes de su exposición se hizo pública una información que revelaba que el origen de estos increíbles anillos pudo ser la fragmentación de una luna en multitud de trozos de cristal, producida por el efecto de la gravedad al aproximarse demasiado al planeta.
Finalmente explicó que las espectaculares formaciones del “señor de los anillos” del Sistema Solar no serán eternas: de hecho, cada día llueven sobre la superficie de Saturno infinidad de trozos de estas formaciones, alrededor de una tonelada por segundo, algo que ha llevado a los científicos a calcular que los anillos de Saturno desaparecerán en unos 300 millones de años.

Las explicaciones sobre Saturno le llevaron a realizar varios apuntes sobre el resto de los cuatro planetas del Sistema Solar que están rodeados por anillos. La científica mencionó el caso de Júpiter e incluso aportó una imagen exclusiva procesada por su compañero Ricardo Hueso unos días antes: explicó que estos anillos, que son mucho más “tenues” que los de Saturno y muy difíciles de observar desde la Tierra, fueron descubiertos por las sondas espaciales Voyager hace 45 años y están integradas por partículas de tierra minúsculas, del diámetro de un cabello humano.
El caso de Urano es diferente: su sistema es “mucho más desconocido” porque se trata de un planeta del que apenas se tienen datos. Lo que sí se sabe es que cuenta con un sistema de 13 aros mucho más finos, que también están integrados por cristales de hielo y por componentes orgánicos probablemente oscurecidos a causa de la radiación. Su repaso a los planetas anillados del Sistema Solar concluyó con Neptuno, del que dijo que sus cinco anillos son más parecidos a los de Júpiter y su composición es orgánica aunque con una proporción mayor de polvo, de entre un 20 y un 70%.
Pero, ¿son los planetas los únicos astros con anillos? ¿Solo se han descubierto estas formaciones en el Sistema Solar? Naiara Barrado-Izagirre respondió con un “no” a ambas preguntas: algunos planetas enanos y centauros son también anillados, mientras que fuera de nuestro Sistema Solar se ha descubierto un planeta con “el sistema más impresionante del Universo”. Se trata del planeta extrasolar J1407B, del que se cree que tiene 37 anillos 200 veces más grandes que los de Saturno.
Y los planetas enanos, ¿qué son y por qué se llaman así? Aunque su nombre apunte a una cuestión de tamaño, los planetas enanos, entre los que se encuentran Plutón, Makemake, Haumea, Eris y Ceres, se denominan así porque incumplen una de las condiciones que deben tener los planetas: además de girar directamente alrededor del sol y de ser lo suficientemente esféricos, los astros convencionales deben haber limpiado la órbita en la que son dominantes o, al menos, ser las formaciones dominantes en ella. Y ninguno de los cuatro cumple esta condición. En el caso de Haumea, miembros del Observatorio de Andalucía observaron su anillo mientras comprobaban sus características, si tenía atmósfera, etc. De esta forma, descubrieron también su forma elipsoidal.
¿Y los centauros? Al margen de su consideración de criatura mitológica, son cuerpos considerados “menores” que se encuentran a caballo entre los asteroides y los planetas, y cuyos anillos son “más densos de lo que se podría esperar”.
Estos ejemplos nos muestran cómo los anillos, a pesar de encontrarse muy lejanos, se encuentran, al mismo tiempo, cada vez más y más cerca de nosotros.
Si no ve correctamente el vídeo use este enlace.
Para saber más:
¿Por qué Júpiter no tiene unos anillos tan espectaculares como Saturno?
¿Y si los dinosaurios se hubieran extinguido antes de que se formaran los anillos de Saturno?
Crónica de Roberto de la Calle / GUK
El artículo Naukas Bilbao 2022: La señora de los anillos se ha escrito en Cuaderno de Cultura Científica.
Diferencias en la metilación del ARN según el tipo de cáncer de mama
El equipo de investigación BIOMICS de la UPV/EHU ha investigado las variaciones que se aprecian en las moléculas de ARN —que se encargan de transferir la información del genoma a las proteínas— entre las personas que padecen cáncer de mama y entre las que no lo padecen, así como los cambios que se advierten en función de cada subtipo de cáncer. Los resultados del estudio muestran que la metilación del ARN en los tejidos tumorales es menor que en los tejidos sanos. Además, se observan diferencias según el tipo de cáncer de mama.
El cáncer es una enfermedad que depende de muchos factores y, además, hay muchos tipos de cánceres. Es importante identificar cuáles son los factores de riesgo de padecer cáncer: para ello, se analizan los grupos de población y se comparan las características de quienes padecen cáncer con las de quienes no lo padecen; de ese modo, se ve si las personas que lo padecen tienen una mayor o menor probabilidad de contar con una determinada característica.
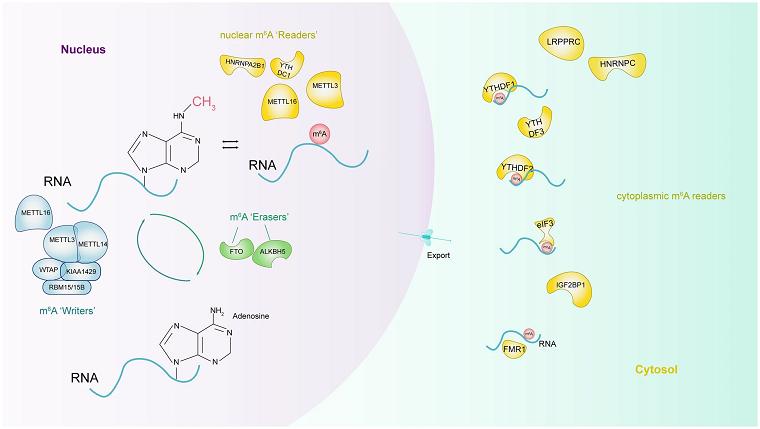 Biología molecular de la metilación del ARN m6A. Fuente: Chen, XY., Zhang, J. & Zhu, JS. (2019) The role of m6A RNA methylation in human cancer. Mol Cancer doi: 10.1186/s12943-019-1033-z
Biología molecular de la metilación del ARN m6A. Fuente: Chen, XY., Zhang, J. & Zhu, JS. (2019) The role of m6A RNA methylation in human cancer. Mol Cancer doi: 10.1186/s12943-019-1033-zEl equipo ha analizado uno de los cambios más frecuentes que se produce en el ARN mensajero: la metilación (adición de un grupo formado por un carbono y tres hidrógenos, en una posición determinada de la molécula de ARN). Un determinado tipo de metilación da como resultado la N6-metiladenosina (m6A). Numerosos estudios han demostrado que la m6A participa en la regulación de la mayoría de los procesos del metabolismo del ARN. Pero aún no se conoce el impacto de este cambio en la regulación de la expresión génica, su función en los procesos celulares y su posible influencia en el desarrollo y avance de enfermedades como, por ejemplo, el cáncer de mama.
Los investigadores han medido la cantidad de m6A presente en el cáncer de mama con el fin de encontrar nuevas dianas terapéuticas en el futuro. “Las metilaciones de m6A son muy frecuentes, ya que se producen para regular la función del ARN. Pero en el cáncer dicha regulación se pierde, y hemos querido observar el papel que juega la metilación del ARN en ese trastorno”, explica Felix Olasagasti, investigador del grupo BIOMICs.
Los resultados muestran que “el porcentaje global de metilación del ARN en los tejidos tumorales es menor que en los tejidos sanos, y la diferencia es significativa”, señala Olasagasti. Además, este es el primer estudio que describe el perfil de metilación de m6A en los diferentes subtipos de cáncer de mama: “Hemos visto que la diferencia detectada en la metilación de las células cancerosas aparece con distinto perfil en función de cada tipo de cáncer de mama. Los cánceres de mama se clasifican según determinadas características. Nosotros hemos visto que, además de las características que se utilizan para dicha clasificación, también hay diferencias en la metilación del ARN en los distintos subtipos de cánceres”.
El investigador subraya la importancia de este hallazgo: “Cuanto mejor conozcamos cómo es o cómo debemos caracterizar cada subtipo de cáncer, más posibilidades tendremos de obtener un tratamiento para combatirlo”. En cualquier caso, el investigador señala que aún queda mucho camino por recorrer. “De este estudio se deduce que la alteración de la metilación podría afectar a las proteínas derivadas de dichos ARN, lo que podría afectar finalmente al carácter canceroso de la célula”. Esa es la hipótesis que manejan los investigadores.
En el estudio han empleado una técnica de secuenciación masiva. “Hemos conseguido un montón de datos. Debemos analizarlos con más detalle para ver en qué genes se producen los cambios. Una vez bien determinados los genes, el siguiente paso sería observar en qué medida afecta eso a las proteínas y ver luego el efecto que eso puede tener. Viendo que el porcentaje de metilación es menor en las células cancerosas, podríamos pensar que aumentar dicho porcentaje podría ayudar a regenerar esas células”. Según Olasagasti, cada uno de esos pasos constituiría un proyecto de investigación.
Para saber más:
¿De dónde viene el cáncer y por qué no ha desaparecido con la evolución?
El cáncer en la nueva era genómica
Referencia:
Tamara Kleinbielen, Felix Olasagasti, Daniel Azcarate, Elena Beristain, Amparo Viguri-Díaz, Isabel Guerra-Merino, África García-Orad, Marian Martínez de Pancorbo (2022) In silico identification and in vitro expression analysis of breast cancer-related m6A-SNPs Epigenetics doi: 10.1080/15592294.2022.2111137
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Diferencias en la metilación del ARN según el tipo de cáncer de mama se ha escrito en Cuaderno de Cultura Científica.
La Geología según Heracles
Heracles es uno de los héroes de la mitología griega más conocido en la actualidad. Sobre todo, con su nombre latinizado, Hércules. Hijo del dios Zeus y de una mortal, Alcmena, su principal característica era su inconmensurable fuerza y el mal rollo que arrastraba con su madrasta olímpica, Hera. Hasta tal punto llegó el odio que le tenía la diosa, que un día volvió loco al héroe forzándolo a matar, con sus propias manos, a su mujer e hijos. Arrepentido, descubrió que la única manera de vivir de nuevo en paz era ponerse al servicio de otro semidiós, el rey Euristeo, con el que tampoco se llevaba demasiado bien. Así que, buscando fastidiar a Heracles, Euristeo le obligó a cumplir doce trabajos, a cuál más complicado, que le llevaron a patearse el mundo conocido enfrentándose a todo mortal, semidiós o monstruo que se le pusiese por delante. Y parece que uno de esos trabajos trajo a Heracles hasta la Península Ibérica.
 Escultura de bronce de Heracles separando las columnas, obra de Ginés Serrán Pagán, erigida en la ciudad de Ceuta. Fuente: Ceuta es turística
Escultura de bronce de Heracles separando las columnas, obra de Ginés Serrán Pagán, erigida en la ciudad de Ceuta. Fuente: Ceuta es turísticaSu décimo trabajo consistía en robar el ganado de Gerión, un monstruo que habitaba en lo que actualmente es Cádiz. Pues según una versión no muy conocida de la historia, en su viaje Heracles atravesó los bosques del norte de la Península y allí se encontró con la ninfa Pyrene, de la que se enamoró perdidamente. Pero el padre de la muchacha no estaba muy de acuerdo con esa relación, por lo que expulsó al héroe de sus tierras y prohibió a la pareja volver a verse. Entonces, Gerión se encontró con la joven y también se enamoró de ella, pero Pyrene no le hizo ni caso porque aún pensaba en Heracles. Gerión, un abusador en toda regla, persiguió a la muchacha hasta lo profundo del bosque con la intención de raptarla, llegando a prenderle fuego para hacerla salir de su escondite. Aunque consiguió todo lo contrario, ya que Pyrene prefirió morir abrasada a caer en sus manos. Cuando Heracles se enteró de lo que pasaba corrió a salvarla, pero llegó tarde. Roto de dolor, decidió hacerle un túmulo funerario como nunca antes se había visto, por lo que se puso a apilar rocas sin cesar. Pero se le fue un poco la mano, llegando a crear un enorme mausoleo rocoso al que llamó Pirineos en honor a la joven.
Volviendo a la versión más conocida de la historia, Heracles cruzó el Mediterráneo para llegar hasta los dominios de Gerión, pero se encontró con que una masa de tierra separaba el mar del océano Atlántico y no le permitía avanzar. Como dar un rodeo no era una opción y haciendo honor a lo bruto que era, separó la cordillera que estaba unida dejando un estrecho pasillo de agua, el estrecho de Gibraltar. Y para conmemorar su hazaña, levantó dos montes uno a cada lado del estrecho, uno en el actual Gibraltar y otro en la actual Ceuta, que pasaron a la posteridad con el nombre de “las Columnas de Hércules”.
Dejando de lado la mitología y acudiendo a la ciencia, lo más llamativo de estas leyendas es que se le da un mismo origen a la cordillera de los Pirineos y las montañas del Arco de Gibraltar. Incluso, se cuenta que el estrecho estuvo cerrado y surcado por una cordillera continua entre el sur de la Península Ibérica y el norte de África que luego se separó, permitiendo así la conexión entre el Mediterráneo y el Atlántico. Y digo que es llamativo porque, con algunos matices, geológicamente hablando todo esto es cierto.
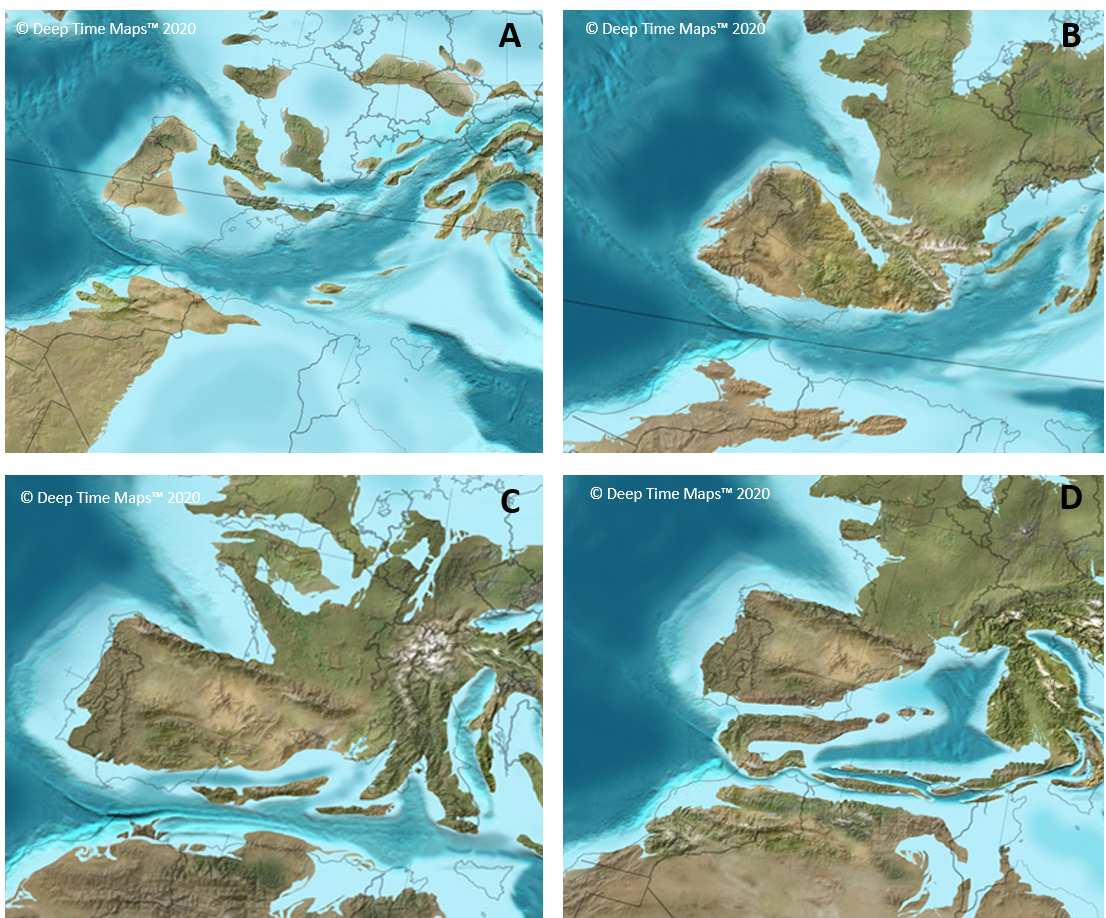 Reconstrucciones paleogeográficas de la Península Ibérica durante diversas fases de la Orogenia Alpina. A) Cretácico, hace 75 millones de años; B) Eoceno, hace 50 millones de años; C) Oligoceno, hace 25 millones de años; y D) Mioceno, hace 13 millones de años. Fuente: Deep Time Maps
Reconstrucciones paleogeográficas de la Península Ibérica durante diversas fases de la Orogenia Alpina. A) Cretácico, hace 75 millones de años; B) Eoceno, hace 50 millones de años; C) Oligoceno, hace 25 millones de años; y D) Mioceno, hace 13 millones de años. Fuente: Deep Time MapsSi cambiamos el nombre Heracles por Orogenia Alpina, ya tenemos la explicación científica. Una orogenia es el proceso de formación de sistemas montañosos por la colisión de dos placas con litosfera continental y la Orogenia Alpina es el último de estos procesos, que comenzó hace unos 80 millones de años y continúa en la actualidad. En este periodo, la placa Africana y la placa Euroasiática se han ido acercando una a la otra, quedando la microplaca Ibérica aprisionada entre ambas. De esta manera, el choque de Iberia con Eurasia en el norte dio lugar al levantamiento de los Pirineos, mientras que el choque de Iberia con África en el sur generó la Cordillera Bética y su continuación por las montañas del Rift en una disposición más o menos arqueada. Es decir, que ambas cordilleras se formaron por el mismo proceso geológico.
 Aspecto del Mediterráneo hace unos 5,5 millones de años, tras el cierre de la conexión con el océano Atlántico. Fuente: Paubahi / Wikimedia Commons.
Aspecto del Mediterráneo hace unos 5,5 millones de años, tras el cierre de la conexión con el océano Atlántico. Fuente: Paubahi / Wikimedia Commons.Pero hay más. Hace casi 6 millones de años, la comunicación entre el Mediterráneo y el Atlántico se vio interrumpida por el continuo acercamiento de las placas Africana e Ibérica, dando lugar al aislamiento y la desecación del Mediterráneo, cuyo nivel llegó a bajar hasta mil metros con respecto a la actualidad. Sin embargo, hace poco más de 5 millones de años, los pulsos tectónicos, combinados con ascensos del nivel del mar, provocaron que el Estrecho de Gibraltar se abriera, dando lugar a un enorme cañón submarino de varios cientos de metros de altura por el que se precipitaba una cascada de agua desde el Atlántico. Así, el Mediterráneo volvió a llenarse rápidamente de agua hasta mostrar el aspecto con el que le conocemos actualmente. A este proceso se le conoce como “Crisis de Salinidad del Messiniense”.
Sé que no he entrado demasiado en detalle con la explicación científica, pero es porque esta vez quería centrarme más en la curiosidad mitológica. Los mitos y leyendas siempre han pretendido dar una explicación más o menos racional a procesos naturales que no éramos capaces de comprender antes del nacimiento de la ciencia. Aunque a veces nos sorprende lo cerca que se encontraban de la verdadera explicación, como suponer que el Mediterráneo quedó aislado del Atlántico por una masa de tierra y que volvió a abrirse por la fuerza de un protagonista que, a su vez, dio lugar a una enorme cordillera en el norte de la Península y a los relieves montañosos del sur de Iberia y el norte de África. Ahora, simplemente, le hemos dado otro nombre a ese protagonista.
Agradecimientos: Quería dar las gracias a mi compañera y amiga Ana Ruiz Constán, científica titular del Instituto Geológico y Minero de España (IGME-CSIC), por recordarme estas leyendas en una agradable conversación geológica.
Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU
El artículo La Geología según Heracles se ha escrito en Cuaderno de Cultura Científica.
Gloria Conyers Hewitt, la clase de profesora que todo estudiante debería tener
Gloria [Conyers Hewitt] exigía trabajar a sus estudiantes y estaba dispuesta a pasar la cantidad de tiempo necesario para ayudarlos a tener éxito. Era la clase de profesora que todo estudiante debería tener.
 Gloria Conyers Hewitt. Fuente: BlackPast.
Gloria Conyers Hewitt. Fuente: BlackPast.
Gloria Conyers nació en Sumter (Carolina del Sur) el 26 de octubre de 1935. Su padre, Emmett C. Conyers, era impresor y su madre, Crenella Clinkscales, maestra. Gloria era la cuarta de los hijos del matrimonio. Sus padres estaban convencidos de que la educación era la única manera de progresar para un afroamericano; por ello animaron a sus tres hijos y a su hija a estudiar.
Estudiar, el objetivo primordialGloria estudió su primer año de enseñanza primaria en casa, con su madre, y después ingresó en la escuela de Moore. Este centro estaba a más de tres kilómetros de su casa; Gloria caminaba cada día para recibir allí sus clases. Al terminar el séptimo grado estudió durante un año en la escuela secundaria local, y después entró en la Academia Mather en Camden, un centro de gran calidad que supuso un gran esfuerzo económico a la familia.
En 1952 ingresó en la Universidad Fisk (Nashville), un centro para afroamericanos orientado principalmente a la formación de docentes. En aquellos tiempos, una mujer afroamericana que deseaba trabajar estaba prácticamente abocada a convertirse en maestra. Lee Lorch era el jefe de matemáticas en aquella institución; era un conocido activista por los derechos civiles y defendía la igualdad de oportunidades de las personas afroamericanas. Gloria no tuvo buenos resultados en el examen de ingreso y la destinaron a una clase de matemáticas de nivel inferior. Obtuvo muy buenas calificaciones y Lorch le aconsejó que se matriculara en la asignatura de cálculo en su segundo año.
Recuerdo que cuando cursé cálculo en la Universidad, el único libro que llevé a casa durante las vacaciones de Navidad fue mi libro de cálculo. Quería hacer esos problemas. Trabajé un problema durante dos semanas antes de conseguir solucionarlo. No era tan difícil, simplemente no entendía el procedimiento de solución. Cuando lo comprendí, ¡estaba tan contenta! No creo que nunca me hubiera sentido tan recompensada. Fue un gran avance. Me enganché.
Gloria Conyers
En mayo de 1954, Gloria se casó con Ronald Hewitt. Sus padres recibieron la noticia con disgusto; su deseo de dar la mejor educación a su hija pequeña estaba en peligro. Gloria y Ronald tuvieron un hijo, Randy Lattimore, y Emmett C. Conyers, que ya no trabajaba, se ofreció para cuidar a su nieto para que Gloria volviera a estudiar. Ella eligió formarse como docente de matemáticas en enseñanza secundaria, graduándose en 1956. Se divorció ese mismo año.
Por recomendación de Lorch, le ofrecieron un puesto de asistente de enseñanza para asistir a la escuela de posgrado en matemáticas en la Universidad de Washington. Lo aceptó, a pesar de que temía estar mal preparada para seguir los cursos. Gracias a que sus padres se ocupaban de su hijo, Gloria siguió estudiando a pesar de las dificultades, y comenzó su tesis con Richard Scott Pierce como tutor.
Hewitt obtuvo una maestría en 1960 y, en 1961, fue nombrada profesora de matemáticas en la Universidad de Montana. Este trabajo le permitió ocuparse de su hijo y, mientras le cuidaba e impartía sus clases, finalizó su tesis doctoral por la Universidad de Washington en 1962: Direct and Inverse Limits of Abstract Algebras.
Hewitt y la situación de las mujeres en matemáticasEn 1971, durante una reunión de la Mathematical Association of America, Hewitt participó en una discusión sobre la situación de las mujeres en matemáticas. El siguiente resumen apareció en el número de noviembre de 1971 de la American Mathematical Monthly:
La profesora Hewitt declaró que nadie puede negar la existencia de prácticas discriminatorias contra las mujeres en matemáticas. Con demasiada frecuencia, en la toma de decisiones para contratar mujeres, el estado civil, las responsabilidades familiares, el tamaño de la familia, etc., son factores influyentes. Se invocan, o se inventan, reglas de nepotismo para justificar nombramientos marginales sin beneficios complementarios o para rechazar a la solicitante, mientras que debería suponerse que la solicitante deseará un empleo permanente, regular y a tiempo completo, a menos que exista evidencia clara de lo contrario. Las recomendaciones que acompañan a las solicitudes para mujeres a menudo respaldan el mito de que las mujeres son un mal riesgo. […] Para hombres y mujeres en condiciones equivalentes, hay también a menudo grandes discrepancias en los salarios, beneficios complementarios, obligaciones departamentales o nombramientos para comités departamentales clave. Las promociones son mucho más lentas para las mujeres que para los hombres. Los criterios deben ser los mismos para todos.
En 1979 Hewitt publicó The status of women in mathematics (La situación de las mujeres en matemáticas) en los Anales de la Academia de Ciencias de Nueva York.
Cuando se menciona a muchas mujeres matemáticas, es por sus actividades más seculares, particularmente cuando se relacionan con las vidas de hombres famosos. Esto, sin duda, ayuda a perpetuar el mito de que las matemáticas son un dominio masculino.
Gloria Hewitt, The Status of Women in Mathematics
La clase de profesora que todo estudiante debería tenerHewitt lamentaba no haber podido emprender más proyectos de investigación en su universidad. A pesar de ello, consiguió publicar varios artículos y redactó algunos informes sobre su especialidad, la teoría de grupos y el álgebra abstracta.
Tras 38 años trabajando en la Universidad de Montana, se jubiló en mayo de 1999 y le fue concedido el título de Profesora Emérita. Entre las muchas razones para concederle este título se aludía a su importante labor como gestora. Y, fundamentalmente, se destacaba su trabajo como docente y mentora de numerosos estudiantes.
Referencias
-
Gloria Hewitt, Biographies of Women Mathematicians, Agnes Scott College
-
O’Connor, John J.; Robertson, Edmund F., Gloria Conyers Hewitt, MacTutor History of Mathematics archive, University of St Andrews
-
Randy Lattimore, Gloria Hewitt: Mathematician, The Mathematics Teacher vol. 94, no. 1 (2001) 9-13
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Gloria Conyers Hewitt, la clase de profesora que todo estudiante debería tener se ha escrito en Cuaderno de Cultura Científica.
Einstein y los experimentos mentales
Si bien casi todo el mundo se ha planteado alguna vez un “¿qué pasaría si…?” para intentar resolver un problema, pocas personas han sabido sacarle tanto provecho como Albert Einstein. Einstein llevó estos experimentos mentales, o Gedankenexperimenten como él los llamaba siguiendo a Mach, a nuevas cotas, creando formas únicas de visualizar un problema que no requerían que se llevase a cabo una prueba física.
 Foto: Bruce Christianson / Unsplash
Foto: Bruce Christianson / UnsplashLos experimentos mentales no eran nada nuevo para los científicos, aunque pocos los elevaron a la categoría de arte como Einstein. Uno de los pensadores más admirados por Einstein, Ernst Mach, también basaba buena parte de su trabajo en esos juegos mentales, y es posible que Einstein le imitase desde una edad bastante temprana. En sus “Notas autobiográficas”, Einstein describe uno de sus experimentos mentales más fructíferos, con el que jugueteó por primera vez cuando tenía dieciséis años. Imaginó como sería ir montado en un rayo de luz.
Viajando a esas velocidades tan increíbles, la misma velocidad que la misma luz, ¿qué vería uno? ¿Qué aspecto tendría una onda electromagnética? ¿Parecería congelada en su movimiento? ¿Qué pasaría si uno iba montado en un rayo de luz que se alejaba de un reloj? Volviendo la vista atrás, el reloj parecería estar congelado, ya que las nuevas ondas de luz que te mostrarían un cambio en el tiempo marcado no te podrían alcanzar. ¿Qué implicaba esto para el tiempo mismo? Preguntas como estas estuvieron revoloteando por la cabeza de Einstein durante años, y encontraron una respuesta en 1905, cuando en varias semanas alumbró la teoría especial de la relatividad. Su nueva teoría afirmaba que incluso si estás viajando a velocidades cercanas a la de la luz, nunca podrás percibir la luz como congelada. En vez de eso, parecerá que se aleja de ti a los mismos 300.000 km/s de siempre. La teoría también decía que si el tiempo parecía estar congelado detrás de ti, entonces desde tu perspectiva ese marco de referencia estaba congelado, anclado para siempre en ese punto.
La teoría general de la relatividad de Einstein también tuvo su germen en un experimento mental, uno al que Einstein se refirió como “el pensamiento más feliz de mi vida”. Tras la publicación de la teoría especial de la relatividad, que describía tan bien cómo se movía la luz, Einstein quería aplicar el concepto a la gravitación. El problema era que la gravitación causaba aceleración y eso parecía bastante diferente a la luz y su única velocidad. Al igual que el anterior, este problema, de una forma vaga, rondó la cabeza de Einstein durante años.
Un día imaginó qué sentiría si estuviese cayendo libremente. De forma muy parecida a ir montado en un rayo de luz, visualizó montar la fuerza de la gravedad y se dio cuenta de que en un una caída libre uno no sentiría la gravedad. Por ejemplo, si Alicia cierra sus ojos mientras cae por la madriguera de conejo más vertical y larga que han conocido los siglos, y no pudiese ver pasar los juegos de té en las estanterías mientras cae, y si, de alguna manera no pudiese sentir el viento, no se daría cuenta de que está cayendo realmente. Fijémonos en que no cae a una velocidad constante, sino que va uniformemente más rápido, acelerándose debido a la gravedad. A pesar de ello, ella sentiría que está simplemente suspendida en el espacio. Si ella, estando en movimiento uniformemente acelerado, sentiría lo mismo que si estuviese quieta, entonces, de repente, Einstein tenía el punto de partida para relacionar su marco de referencia en aceleración con el de alguien en reposo observándola. Si los dos marcos de referencia se percibían iguales, Einstein podía crear ecuaciones partiendo de la hipótesis de que eran idénticos. La teoría general de la relatividad nació poco después.
Tras la teoría general de la relatividad Einstein dedicó su atención a la física atómica e hizo uso de sus Gedankenexperimenten una vez más. Todavía se recuerdan sus ardientes disputas con Niels Bohr acerca de cómo interpretar la nueva mecánica cuántica e, invariablemente, Einstein empleó experimentos mentales para apoyar sus ideas. Desde rayos de luz atravesando rendijas a cajas colgando de una balanza, Einstein empleó tantas situaciones como pudo para intentar convencer a Bohr y sus colegas. Uno de los últimos grandes artículos [1] de Einstein, escrito con Boris Podolsky y Nathan Rosen, es un experimento mental que hoy día se conoce como la paradoja EPR, en la que se visualizan dos partículas que están a varios kilómetros de distancia y, sin embargo, son capaces de comunicarse a una velocidad superior a la de la luz. Este Gedankenexperiment fue respondido por Bohr [2], al igual que tantos otros de los experimentos mentales cuánticos, de una manera que no satisfizo necesariamente a Einstein, pero sí al resto de la comunidad científica. Paradójicamente, muchos de los experimentos mentales de Einstein que tuvieron que ver con la mecánica cuántica terminaron ayudando a cimentar la nueva dinámica en los cerebros de sus defensores, exactamente lo contrario de lo que pretendía Einstein.
El famoso historiador de la ciencia Gerald Holton, que ha estudiado a Einstein de forma exhaustiva y ha intentado describir qué hizo a su cerebro tan creativo y fructífero, cree que estos experimentos mentales son parte de la respuesta. Einstein tenía la capacidad de visualizar soluciones a hipótesis tan vívidamente que podía resolver problemas complejos en su cabeza. Los experimentos mentales puede que hayan sido la clave de su genio.
Referencias:
[1] Einstein, A., Podolsky, B., & Rosen, N. (1935). Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? Physical Review, 47 (10), 777-780 DOI: 10.1103/PhysRev.47.777
[2] Bohr, N. (1935). Can Quantum-Mechanical Description of Physical Reality be Considered Complete? Physical Review, 48 (8), 696-702 DOI: 10.1103/PhysRev.48.696
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Una versión anterior de este artículo se publicó en Experientia Docet el 13 de junio de 2010.
El artículo Einstein y los experimentos mentales se ha escrito en Cuaderno de Cultura Científica.
Extinción en los mares
Los biólogos marinos han detectado una tendencia, muy actual, a la extinción de especies marinas y, para observar mejor sus efectos en la ecología, evolución y biodiversidad de los mares y en la, esperemos, recuperación de este riesgo, Jonathan Payne y su grupo, de la Universidad de Stanford, la han comparado con otras extinciones anteriores que conocemos por el registro fósil. Analizan una base de datos con 2497 especies, extinguidas y actuales, de moluscos y de vertebrados marinos. Solo estudian especies de géneros que existen extinguidos y vivos, para facilitar las comparaciones. El riesgo de extinción lo toman de las listas de la Unión Internacional para la Conservación de la Naturaleza (IUCN). Comparan cuatro aspectos de estas especies: tamaño del cuerpo según la longitud máxima; hábitat bentónico, en el fondo, o pelágico, en aguas libres; movilidad según sean móviles o inmóviles; y alimentación según sean predadores o no predadores.
La comparación con las cinco extinciones anteriores, que conocemos por el registro fósil, muestra que la extinción actual es más fuerte para los animales de gran tamaño, y más leve para los animales móviles que para los inmóviles. No tiene diferencias según el hábitat, bentónicos o pelágicos, ni según la alimentación, sean predadores o no predadores.
Los autores proponen que la extinción más grave para los animales grandes se debe a la actividad humana y, en concreto, a la pesca en el mar que busca los ejemplares de mayor tamaño por ser más aprovechables. Algo parecido ocurrió en tierra y, así, nuestra especie ha contribuido a la extinción de mamuts, moas, tortugas gigantes y otras especies de gran tamaño.
 Foto: Gabriel Dizzi / Unsplash
Foto: Gabriel Dizzi / UnsplashEl grupo de Douglas McCauley, de la Universidad de California en Santa Barbara, revisa lo que sabemos de esa extinción de especies provocada directamente por la actividad humana. Es un proceso que comenzó a gran escala hace tiempo y se aceleró en los últimos siglos y, sobre todo, en el siglo XX. McCauley investiga los últimos 55000 años y, aunque desaparecen especies terrestres como las que he mencionado, en el mar las extinciones comenzaron mucho más tarde. Además, las especies marinas tienen una dispersión geográfica más amplia que las especies terrestres y no es habitual que se encuentren tan localizadas y, por tanto y en general, tienen un menor riesgo de extinción rápida que las terrestres. Sería interesante comparar la extinción de las especies marinas con las que se han detectado en aves, cuya dispersión y movilidad es parecida. Y, como ocurría en el estudio de Payne, son las especies de mayor tamaño las más amenazadas.
Un estudio reciente, publicado en 2022 por Justin Penn y Curtis Deutsch, de las universidades de Washington en Seattle y de Princeton, confirma los resultados de Jonathan Payne en la extinción en los océanos a partir de modelos con datos del calentamiento global y su influencia sobre la ecología y la fisiología de varias especies. Confirman lo que presentan los modelos con lo que se conoce de extinciones anteriores según el registro fósil.
En los modelos, el aumento de la emisión de gases con efecto invernadero, la pérdida de especies por el calentamiento y la disminución de oxígeno en la atmósfera es comparable al impacto directo de nuestra especie en este siglo y culmina en una extinción como las anteriores en la historia del planeta. Son las especies polares las que tienen más riesgo de extinción pero donde más disminuye la riqueza en biodiversidad es en las áreas más ricas, en concreto en los trópicos. Con el control del cambio climático por disminución del calentamiento global, según las conclusiones de los autores, bajaría el riesgo de extinción en más de un 70%.
Extinción por tamañoUn ejemplo de extinción según el tamaño sería caso de los cetáceos, mamíferos marinos que pueden alcanzar gran tamaño, según el estudio de Chuanwu Chen y su equipo, de la Universidad Normal de Nanjing, en China. La ballena azul, Balaenoptera musculus, es el mayor animal actual del planeta Tierra. Se dividen en dos subclases: misticetos y odontocetos. Los misticetos, sobre todo ballenas, se caracterizan por tener barbas para el filtrado de agua de mar y retener el alimento, y los odontocetos, como cachalotes o delfines, tienen dientes. En total son 90 especies y, de ellos, 80 tienen un seguimiento en la Lista Roja de la Unión Internacional para la Conservación de la Naturaleza. De todos ellos, 22 especies, el 27.5%, están en riesgo de extinción. De las 80 especies, 13 son misticetos y 67 son odontocetos. El porcentaje de especies en peligro es mayor en misticetos con 5 de 13, el 38.5%, que en odontocetos con 17 de 67, el 25.4%.
Los factores que más llevan al riesgo de extinción a estas especies son el tamaño, la distribución geográfica, la temperatura de la superficie del mar y los riesgos concretos por la acción de la especie humana. Es curioso que en misticetos, a mayor tamaño, más riesgo de extinción, mientras que en odontocetos es al contario y con más tamaño hay menos riesgo. También es destacable que, de los siete posibles riesgos de extinción, el más peligroso es la pesca al azar. Se busca otro pescado y se capturan cetáceos sin buscarlo.
Cuando una especie sufre un proceso de extinción, su rango de distribución geográfica se contrae, se hace menor, pues son las zonas periféricas de esa distribución las que primero desaparecen. En la periferia, la población habitualmente es menor y tiene condiciones ambientales más difíciles y, por ello, son las primeras en desaparecer. McCauley ha investigado cuales son las especies cuyo rango geográfico se ha contraído. De nuevo son las especies terrestres las que más han pasado por esta disminución de rango, incluyendo, entre las especies que destaca, algunas cabras y mariposas que han desaparecido. En el mar, de nuevo las especies de gran tamaño, tiburones en concreto, son las que más han contraído su rango de distribución.
También se están perdiendo algunos hábitats muy concretos en el mar, como algunos arrecifes de coral que, para 2007, se consideraba que habían disminuido en un 30%, o los manglares, con un 20%, y siempre, según la hipótesis que proponen los expertos, por el aumento de la temperatura del agua del mar por el calentamiento global. Y, también, por otras actividades de nuestra especie, como el aumento del número de molinos eólicos marinos, los contratos de minería submarina en aguas internacionales, el tráfico de contenedores, que ha aumentado en un 600% desde 1970, y el número de las llamadas “zonas muertas”, sin oxígeno, que hay en el mar.
Más vidas que un… pulpoSin embargo, si entramos en casos concretos, no todo son malas noticias y ocurre, por ejemplo, con los cefalópodos. Son un grupo de moluscos marinos, con unas 700 especies, y los más conocidos son los pulpos, los calamares, las sepias,… Además de su importancia en la biología y la ecología del mar, también son muy apreciados en la gastronomía. Tienen un crecimiento rápido, un ciclo de vida corto y una gran plasticidad para adaptarse a condiciones ambientales cambiantes. Como cuentan Zoe Doubleday y sus colegas, de la Universidad de Adelaida, en Australia, y de otros centros de todo el mundo, entre ellos el Instituto Español de Oceanografía de Palma de Mallorca, parece que las poblaciones de cefalópodos están aumentando en todos los mares del planeta según los datos de capturas en las pesquerías de estos animales.
Para confirmarlo, Doubleday y su grupo hacen un meta-análisis de lo publicado sobre pesquerías de cefalópodos en los últimos 61 años, desde 1953 a 2013. Utilizan datos de todas las regiones oceánicas y cifras de capturas de las especies más importantes por su comercialización, como el pulpo o el calamar, y así hasta 35 especies.
Los resultados demuestran que la abundancia de cefalópodos ha crecido en los 61 años revisados y, además, en todos los hábitats, tanto bentónicos, en el fondo, como demersales, que viven cerca del fondo, o pelágicos, que viven en aguas libres.
Las causas de este aumento de los cefalópodos están en discusión, con hipótesis como el cambio climático, con la subida de la temperatura del agua que, a su vez, acelera los ciclos de vida de estos animales. O la caída de las poblaciones de los peces que se alimentan de cefalópodos por sobreexplotación pesquera y, en consecuencia, al tener menos depredadores la población de cefalópodos crece.
La cuestión abierta de los arrecifes de coral Foto: Francesco Ungaro / Unsplash
Foto: Francesco Ungaro / UnsplashOtro debate que sigue abierto es la desaparición de los arrecifes de coral, sobre todo en el Caribe y el Pacífico y, de nuevo, por causa del calentamiento global. El equipo de Jennifer Smith, de la Institución Oceanográfica Scripps de La Jolla, en California, ha publicado que, en el Caribe, la extensión de los arrecifes ha caído un 80% en los últimos 30 años. En el Pacífico ha desaparecido un 50% desde los ochenta a los primeros 2000. Las predicciones de los expertos apuntan a la extinción de un 70% para mediados de este siglo.
Para estudiar en detalle lo que está ocurriendo con los arrecifes de coral, el grupo de Smith ha examinado en detalle las comunidades de arrecifes, durante diez años, en 56 islas de cinco archipiélagos del centro del Pacifico. El estudio lo han hecho sobre 6500 fotografías de los fondos con arrecifes tomadas en 450 puntos de muestreo de las 56 islas.
Los resultados demuestran que el daño a los arrecifes se produce en los más cercanos a alguna población humana. En las islas deshabitadas, los arrecifes mantienen las especies habituales en estos hábitats.
Los efectos perjudiciales sobre los arrecifes de corales son, según el grupo de Renee Setter, de la Universidad de Hawaii en Manoa, las olas de calor en el mar, la acidificación del agua, las tormentas, la contaminación que llega desde tierra, y las sustancias estresantes humanas que se vierten en zonas concretas. Según los autores, estos efectos se estudian cada uno por separado pero, cuando se hace en conjunto, el daño es mayor que la suma de todos ellos. Por ejemplo, las condiciones ambientales serán insostenibles para 2050, en 28 años, para cada efecto por separado, pero serán insostenibles para 2035, en 13 años solamente, cuando se analizan en conjunto. En el mejor escenario, con mitigación de gases con efecto invernadero y un desarrollo humano optimista para la sostenibilidad, para 2100 el 41% de los corales serán insostenibles pero, si se analizan los efectos en conjunto, para finales del siglo XXI el 64% serán insostenibles. En el peor escenario, para 2055, el 99% de los corales no serán sostenibles.
En cambio, los arrecifes de ostras parece que siguen un camino diferente a los de coral. El grupo de Michael Beck, de la Universidad de California en Santa Barbara, ha revisado lo que conocemos sobre la progresiva disminución de los arrecifes de ostras.
Han repasado los datos de 144 bahías y 44 regiones costeras de todo el mundo. Alrededor del 90% han perdido las ostras, incluyendo la costa atlántica de la Península Ibérica. Los pocos ejemplares que quedan en muchos de los lugares estudiados no suponen poblaciones funcionales para la ecología del entorno ni para el éxito reproductor de la propia especie. En conclusión, más del 75% de las bahías han perdido su población de ostras. Han intervenido en su desaparición la sobrepesca y la contaminación, sobre todo en los estuarios con una gran población humana.
Sin embargo, las pesquerías de ostras se conocen desde hace milenios según el estudio de Leslie Reeder-Myers y sus colegas, de la Universidad Temple de Philadelphia, sobre los yacimientos indígenas de Norteamérica y Australia. Explotados durante mucho tiempo con permanencia en el espacio y en el tiempo durante 5000-10000 años, y las pesquerías de ostras pueden incluso más antiguas.
Los autores repasan en detalle nueve especies en 6 yacimientos de Queensland, en Australia, 21 en la costa oeste de Norteamérica, y 43 en la costa este. Sin embargo, la comparación con las pesquerías actuales demuestra que el 85% de las zonas con arrecifes de ostras se han perdido en el inicio de este siglo con el cambio de la explotación con métodos indígenas al sistema comercial capitalista que ha diezmado las poblaciones.
Referencias:
Baeck, M.W. et al. 2011. Oyster reefs at risk and recommendations for conservation, restoration and management. BioScience 61: 107-116.
Chen, C. et al. 2022. Geographic range size, water temperature, and extrinsic threats predict the extinction risk in global cetaceans. Global Change Biology DOI: 10.1111/gcb.16385.
Doubleday, Z.A. et al. 2016. Global proliferation of cephalopods. Current Biology 26: R406-R407.
McCauley, D.J. et al. 2015. Marine defaunation: Animal loss in the global ocean. Science doi: 10.1126/science.1255641
Payne, J.L. et al. 2016. Ecological selectivity of the emerging mass extinction in the oceans. Science doi: 10.1126&science.aaf2416
Penn, J.L. & C. Deutsch. 2022. Avoiding ocean mass extinction from climate warming. Science 376: 524-526.
Reeder-Myers, L. et al. 2022. Indigenous oyster fisheries persisted for millennia and should inform future management. Nature Communications 13: 2383.
Setter, R.O. et al. 2022. Co-occurring anthropogenic stressors reduce the timeframe of environmental viability for the world’s coral reefs. PLOS Biology 20: e3001821.
Smith, J.E. et al. 2016. Re-evaluating the health of coral reef communities baselines and evidence for human impacts across the central Pacific. Proceedings of the Royal Society B 283: 20151985
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo Extinción en los mares se ha escrito en Cuaderno de Cultura Científica.
Las cuerdas frotadas del violín
 Foto Providence Doucet / Unsplash
Foto Providence Doucet / UnsplashLos instrumentos musicales de cuerda frotada han ocupado un lugar especial en la música durante muchos siglos. Los violines, y toda su actual familia moderna (viola, violonchelo y contrabajo) constituyen no solo la columna vertebral de las orquestas sinfónicas y de cámara, sino que además son instrumentos solistas que pueden sonar y cantar con voz característica melodías inolvidables capaces de conectar directamente con nuestros cerebros.
En principio es sencillo describir el funcionamiento mecánico de un violín. Ello comienza cuando la persona ejecutante pasa el arco por las cuerdas y las hace vibrar. A través del puente y el alma situada dentro del cuerpo del instrumento, la caja de resonancia recibe la vibración de las cuerdas, y al final irradia al aire ondas sonoras moduladas y amplificadas. Es notable que se requiere aplicar muy pocos milivatios de potencia mecánica para hacer funcionar un violín y sin embargo es capaz de generar grandes variaciones de presión sonora en el aire y, por tanto, llenar de sonido una gran sala de conciertos con un solo instrumento.
Cuerdas frotadas vs pulsadas o golpeadasEl movimiento de la cuerda frotada de un violín es muy diferente al de la cuerda pulsada (por ejemplo de una guitarra) y al de la cuerda golpeada (por ejemplo de un piano). Tanto la cuerda pulsada como la golpeada son sistemas mecánicos de condiciones iniciales: la cuerda recibe un desplazamiento o velocidad inicial, tras lo cual la vibración de la cuerda da lugar a un breve movimiento transitorio que decae con el tiempo. Sin embargo, la cuerda frotada es un sistema impulsado por un oscilador de fricción autosostenida. A pesar de que ya existían en los albores de la historia instrumentos musicales de esta naturaleza, los detalles de este movimiento autosostenido son considerablemente más complicados, y no se pudieron describir de forma adecuada durante milenios.
Algo importante para frotar una cuerda es proporcionar una interacción mecánica específica entre el arco y las cuerdas. Los pelos del arco del violín suelen ser crines de caballo entre cuyas células la resina (colofonia) que se aplica queda almacenada y el arco queda pegajoso con un alto factor de fricción estática. La interacción entre el arco y la cuerda frotada en un instrumento fue descrita con detalle por el gran científico Hermann Helmholtz [1] mediante el efecto Ruckgleiten, que se denomina actualmente el mecanismo stick-slip (pegar-deslizar).
El movimiento de HelmholtzEl arco pegajoso arrastra la cuerda, en dirección transversal, hasta que la fuerza de restauración debida a la tensión de la cuerda es mayor que la fricción estática, y la cuerda se desliza moviéndose de nuevo hacia el equilibrio en el sentido opuesto al que se mueve el arco. La cuerda sobrepasa su equilibrio y al llegar a su posición extrema es atrapada y se pega al arco que la arrastra de nuevo. Al repetirse este proceso, la cuerda mantiene la vibración sostenida. Este movimiento continuo se denomina movimiento de Helmholtz porque éste fue el primero en observarlo en 1862 utilizando su «microscopio de oscilación» y las figuras de Lissajous.
Helmholtz descubrió que la forma real de la cuerda en cualquier instante son dos segmentos rectos unidos mediante un codo en un punto. Con un frotamiento de arco ascendente en el violín, este codo recorre en sentido contrario a las agujas del reloj siguiendo una trayectoria parabólica. Con un frotamiento de arco descendente, la rotación es idéntica pero con recorrido del codo en el sentido de las agujas del reloj. Este movimiento tan especial es una forma de onda estacionaria que puede verse en detalle rodando un video a cámara lenta.
Riqueza armónica de las cuerdas frotadasLo mismo que una guitarra, un violín puede hacer sonar las notas musicales acortando o alargando la longitud de las cuerdas para cambiar la frecuencia fundamental de la vibración. Sin embargo, notemos que tal y como Helmholtz observó y dibujó en su libro (p. 83), las cuerdas frotadas vibran según ondas de diente de sierra, que es un tipo de señal acústica muy rica en armónicos. Ello implica que las cuerdas frotadas entregarán al cuerpo del violín no solamente una vibración autosostenida, sino una gran cantidad de armónicos que la caja de resonancia podrá utilizar para enriquecer el espectro acústico del instrumento. Como consecuencia, el empleo de cuerdas frotadas puede dar lugar a superiores características musicales con respecto a otros tipos de cuerdas. Ello incluye poder interpretar todo tipo de sonidos, tanto graves o agudos como de larga o corta duración, así como variado timbre armónico específico del cuerpo del instrumento. Explicamos así el hecho bien conocido de que la voz de la familia del violín se asemeja claramente al canto y a la voz humana.
Referencia
[1] H. Helmholtz, On the Sensations of Tone, 2nd edition, traducido por A. J. Ellis, reimpresa por Dover Publications, 1954, pp. 80-88.
Sobre el autor: Victor Etxebarria Ecenarro está diplomado como lutier por el Conservatorio Juan Crisóstomo de Arriaga (Bilbao) y es Catedrático de Ingeniería de Sistemas y Automática en la Universidad del País Vasco (UPV/EHU)
El artículo Las cuerdas frotadas del violín se ha escrito en Cuaderno de Cultura Científica.
Naukas Bilbao 2022: ‘Hackers’ están diseñando los próximos fármacos

¿Qué tiene que ver Neo, el personaje central de la película Matrix (Lilly y Lana Wachowski, 1999), con el diseño de fármacos personalizados? Acaso, ¿es posible hackear la información genética de los pacientes para crear nuevos medicamentos?
Diseñar fármacos específicos para cada persona ya no es una entelequia propia del cine de ciencia ficción. Gracias a las terapias de ácidos nucleicos los farmacéuticos han comenzado a actuar sobre diferentes momentos del proceso de desarrollo de las enfermedades para atajarlas antes incluso de que se manifiesten o muestren sus síntomas.
La investigadora Ikerbasque en Biocruces Bizkaia y experta en terapias de ácidos nucleicos Virginia Arechavala, utilizó un paralelismo con el personaje de ciencia ficción para explicar en Naukas Bilbao el alcance de este trabajo investigador y sus aplicaciones al mundo de la medicina. Tras recordar que Neo era “un hacker que aprende a cambiar su realidad porque es capaz de leer el código que hay detrás de la realidad virtual en la que vive”, la investigadora recordó que nuestro organismo tiene también un código, en este caso genético, que es el que contribuye a generar las proteínas que necesitamos para vivir.
Para explicar la labor de los investigadores, Virginia Arechavala declaró que cada célula cuenta con información genética que permite generar esas proteínas, y que muchas veces las variaciones y mutaciones que sufre esta información apenas provocan cambios sobre nuestra vida diaria. Sin embargo, hay ocasiones en que esos cambios conllevan manifestaciones diferentes en el cuerpo humano que afectan, por ejemplo, a no tener una proteína especialmente necesaria o generar una tóxica, y que se pueden traducir en enfermedades poco frecuentes.
Con este planteamiento sobre la mesa, la experta en terapias de ácidos nucleicos compartió con el público del Palacio Euskalduna cómo la investigación actual, en lugar de buscar un medicamento que actúen sobre las proteínas responsables de una enfermedad, quieren actuar sobre la información genética que codifica estas proteínas. La investigadora puso como ejemplo la preparación de una paella.
“Conocemos cuál es el proceso por el que se generan las proteínas y los medicamentos que tenemos hasta ahora actúan sobre el resultado final de ese proceso. Sería como ir a una paella ya cocinada –una proteína– y quitarle uno de los ingredientes erróneos con los que se ha preparado, que la hace tóxica”, explicó la experta. De esa forma, el medicamento actúa de forma específica sobre el elemento nocivo para nuestro cuerpo y lo elimina. Sin embargo, en otras ocasiones, ese ingrediente o elemento nocivo es de tal gravedad que no se puede actuar contra él ni atajar la enfermedad.
Frente a este planteamiento convencional, Arechavala indicó que en la actualidad disponemos de la información que nos permite saber para qué sirve cada gen (receta), cómo desde cada gen se cocina cada proteína, y contamos con “cocineros”, los ribosomas, capaces de modificarla durante su “preparación”, con lo cual es posible actuar antes de que esta proteína esté ya “cocinada”. Incluso afirmó que se puede cambiar esa “receta” en origen para conseguir una proteína distinta a la original. “Las vacunas de ARN mensajero se basan en este concepto: si tienes a un cocinero preparado para cocinar le das una receta diferente para que haga lo que tú quieras”, explicó de forma gráfica.

Estas nuevas terapias son especialmente aplicables en el caso de las llamadas enfermedades raras, en las que los cambios genéticos impiden la producción de proteínas indispensables o generan proteínas “tóxicas” que derivan en dolencias que, en ocasiones, son incurables. “Cuando tienes una mutación que genera una proteína tóxica, lo ideal sería no tenerla, es decir, restaurar el gen para suprimir esa mutación nociva y dejarlo como estaba. Esta técnica se llama edición génica y ya se está probando en ensayos clínicos para enfermedades poco frecuentes.”
“Lo siguiente sería la terapia génica, es decir, traer un gen correcto (sin la mutación) hasta el núcleo de las células para que generen la proteína que se necesita”, explicó. Y aunque se trata de una opción compleja porque obliga a distribuir ese gen por todas las células del cuerpo, es una técnica que ya se emplea en algunos medicamentos que están aprobados y disponibles para pacientes con enfermedades poco frecuentes.
Dentro de esta tarea investigadora, Virginia Arechavala mencionó otra opción para corregir estas mutaciones antes de que “se cocinen” estas paellas tóxicas: “Podemos enviar una “anti-receta” que bloquee la receta tóxica para evitar que nuestros ribosomas/cocineros la cocinen y generen una proteína tóxica. ¿Cómo? Mediante el ARN de interferencia”.
Y citó un ejemplo más: “De un mismo gen se pueden obtener un montón de proteínas distintas, un splicing alternativo, que es una especie de ‘elige tu propia aventura’, en la que puedes escoger entre distintos finales según la manera en la que leas el libro. Pues nuestros genes son así, y por eso, como es posible influir en el momento en que eliges cómo va a ser la proteína, se puede actuar sobre ello, como si se pegara un post-it que cambia ligeramente la receta antes de que la lea el cocinero. Es otra terapia de ARN que ya está disponible para enfermedades poco frecuentes”.
Por último, Arechavala apuntó que a pesar de la mayoría de la investigación y los primeros medicamentos de este tipo se han desarrollado para las llamadas enfermedades raras, gracias a los avances que se han conseguido con su impulso, estas terapias pronto se aplicarán al tratamiento de otras dolencias muy comunes, como el colesterol alto, para el que ya hay en el mercado un fármaco específico basado en estos conceptos. “Todos estos medicamentos no son ciencia ficción, podemos encontrar más. Se suele decir que en farmacia hay de todo, como en botica, y probablemente la próxima vez que vayáis a la farmacia podáis encontrar medicamentos diseñados por un hacker”, concluyó.
Si no ve correctamente el vídeo use este enlace.
Para saber más:
50 años modificando genes (en seres humanos)
Una infección vírica puede activar la aparición de diabetes tipo I
Crónica de Roberto de la Calle / GUK
El artículo Naukas Bilbao 2022: ‘Hackers’ están diseñando los próximos fármacos se ha escrito en Cuaderno de Cultura Científica.
Un tapón ecológico para tratar la hemorragia nasal
 Foto: Nagore Iraola. UPV/EHU
Foto: Nagore Iraola. UPV/EHULa hemorragia nasal, también conocida como epistaxis, es una de las urgencias otorrinolaringológicas más frecuentes en todo el mundo. Se calcula que el 60 % de la población mundial sufrirá un episodio de epistaxis al menos una vez en su vida, aunque solo entre el 6% y el 10% de ellos buscará atención médica. Existen varios métodos para tratar la epistaxis y uno de los métodos más populares y con una elevada tasa de éxito es el taponamiento nasal. No obstante, la elección del tapón nasal más adecuado es vital para el resultado del tratamiento. El tapón nasal ideal debe favorecer la hemostasia —el conjunto de mecanismos biológicos para detener los procesos hemorrágicos— y ser cómodo para el paciente, disminuyendo así el daño en la mucosa nasal.
En este trabajo conjunto de los grupos NanoBioCel y BIOMAT de la UPV/EHU, “hemos demostrado que los subproductos de la industria alimentaria son una fuente valiosa y sostenible de biomateriales que pueden emplearse para fabricar tapones nasales seguros y eficaces con grandes propiedades hemostáticas”, señala Edorta Santos Vizcaíno, investigador del grupo NanoBioCel y uno de los autores del trabajo.
“A partir de subproductos naturales de la industria alimentaria —proteína de soja y quitina— hemos desarrollado un scaffold o una matriz esponjosa que presenta una serie de propiedades fisicoquímicas muy interesantes: es capaz de absorber grandísimas cantidades de agua o sangre, tiene mucha superficie para unir y albergar células en su interior, no produce ningún tipo de rechazo contra el material y, además, se degrada parcialmente”, comenta el investigador de la UPV/EHU.
La quitina es la base de esta nueva estructura, es decir, el esqueleto del material esponjoso, mientras que la proteína de soja se encarga de forrar dicha estructura para hacer que el material sea muy biocompatible y a su vez capaz de absorber grandes cantidades de sangre.
Un tapón verde“La creciente necesidad social de ser respetuosos con el medioambiente —comenta el investigador de la UPV/EHU— nos llevó a investigar si el material tipo esponja producido a partir de proteína de soja y quitina puede emplearse como tapón nasal para el tratamiento de la epistaxis”. Para evaluar el potencial de nuestro material como tapón nasal, “hemos analizado su uso como tapón nasal comparándolo con el gold standard actual, Merocel®, fabricado con materiales sintéticos”, añade Santos.
Los ensayos realizados tanto in vitro como in vivo en ratas, “demuestran que el material desarrollado presenta una microestructura porosa con gran capacidad de absorber agua y sangre. Se comprobó que nuestro biomaterial promueve eficazmente la coagulación de la sangre, mostrando excelentes propiedades de unión de glóbulos rojos y plaquetas en comparación con Merocel®. Todo esto es debido a las propiedades hemostáticas intrínsecas de sus componentes naturales”, comenta Edorta Santos. Además, “vimos que es capaz de perder peso en medio acuoso y de degradarse parcialmente en pocos días cuando está sumergido en sangre, característica cada vez más importante para los tapones nasales, ya que de lo contrario su extracción resulta invasiva”, añade el investigador.
En definitiva, “nuestro material producido a partir de desechos de la industria alimentaria mostró propiedades mecánicas y hemostáticas superiores al Merocel®”, concluye Edorta Santos.
El personal investigador de ambos grupos de investigación coincide en que, “este trabajo, realizado desde un enfoque de economía circular, demuestra que se puede seguir una estrategia verde para fabricar tapones nasales utilizando subproductos valorizados de la industria alimentaria, con propiedades hemostáticas incluso mejores que el estándar de oro en la clínica”.
“De hecho, ahora mismo, estamos en vías de solicitud de patente europea tratando de buscar alguna empresa que se interese por el producto para poder materializar la idea y apostar por esta tecnología basada en el concepto de la economía circular”, lanza Edorta Santos.
Para saber más:
Dando valor a los residuos marinos para cuadrar la economía circular
Referencia:
Jon Jimenez-Martin, Kevin Las Heras, Alaitz Etxabide, Jone Uranga, Koro de la Caba, Pedro Guerrero, Manoli Igartua, Edorta Santos-Vizcaino y Rosa Maria Hernandez (2022) Green hemostatic sponge-like scaffold composed of soy protein and chitin for the treatment of epistaxis Materials Today Bio doi: 10.1016/j.mtbio.2022.100273
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Un tapón ecológico para tratar la hemorragia nasal se ha escrito en Cuaderno de Cultura Científica.
El camión solar: ¿una posibilidad real?
Los cálculos son tercos y apuntan a que todavía estamos muy lejos de ver circulando por la carretera un camión solar.
 Gama de soluciones de movilidad apoyada por energía solar fotovoltaica propuesta por Sono Motors. Fuente: Sono Motors
Gama de soluciones de movilidad apoyada por energía solar fotovoltaica propuesta por Sono Motors. Fuente: Sono MotorsLa movilidad del futuro se presenta fascinante y llena de novedades. En los últimos años hemos visto emerger nuevos actores y viejos conocidos con ímpetus renovados. En el extremo ligero de las soluciones de transporte encontramos los patinetes y las bicicletas eléctricas. Para desplazarnos más rápidamente disponemos de turismos eléctricos en diferentes configuraciones y con distintos resultados al respecto de la reducción de emisiones de gases: motorizaciones híbridas, híbridas enchufables y cien por cien eléctricas. En el horizonte inmediato esperan las pilas de combustible, con el potencial de crear un nuevo sector de la economía con el hidrógeno como vector energético. Quizá más allá se encuentren sistemas pesados basados en el ciclo de oxidación-reducción del hierro, con usos prospectivos en el campo naval. Y en el aire encontramos los combustibles de origen vegetal de segunda generación que prometen ciclos casi cerrados y, por tanto, una gran reducción en las emisiones de CO2. La electrificación en el aire espera aún un gran salto en las capacidades de almacenamiento de energía de las baterías eléctricas, que está tardando en darse y no está, bajo ningún concepto, garantizado.
Vehículos con apoyo fotovoltaicoLa movilidad solar ha sido tradicionalmente una curiosidad, limitada a ejemplos experimentales. La realidad es tozuda y se muestra inflexible por lo que respecta a permitir que un vehículo sea independiente de cualquier infraestructura de carga o repostaje. Las aventuras ingenieriles que han buscado derivar toda su capacidad motriz de la energía del sol mediante paneles fotovoltaicos embarcados han fallado una y otra vez. Incluso conseguir que parte de la energía consumida sea de origen solar supone, por lo general, mucha más molestia de la que merece la pena a la luz (exigua) de los resultados.
Sin embargo, entre las propuestas de movilidad que aparecen prácticamente a diario en las noticias tecnológicas empiezan a verse ejemplos de coches solares. Destacan, por su cercanía al mercado, dos modelos: el Sono Sion y el Lightyear 0 (el número cero, no la letra o mayúscula). Ambos utilizan superficies cubiertas de paneles solares poco o nada frecuentes en un vehículo. Capó, techo y portón trasero en el caso del Lightyear [1], una berlina de casi 5,10 metros de longitud, con un total de 5 metros cuadrados de paneles curvados según la aerodinámica de la carrocería. El Lightyear 0 promete nada menos que 70 kilómetros diarios de movilidad solar sin coste, aunque la letra pequeña afirma que el cálculo está hecho para una ubicación no especificada del sur de España y solo es válido durante el 10 por ciento del año más favorable, alrededor del solsticio de verano. Este dato sin duda será interesante para los potenciales compradores de la berlina que vivan más cerca de la sede de la marca, en Eindhoven (Países Bajos).
 Lightyear 0. Fuente: Lightyear
Lightyear 0. Fuente: LightyearEn cuanto al Sono Sion [2], un monovolumen de 4,47 metros de longitud, ofrece ocho metros cuadrados de paneles fotovoltaicos integrados en todas las superficies expuestas de la carrocería. No solo capó y techo, sino también puertas y aletas. El cálculo de la autonomía solar que permite sus paneles está dado por el fabricante en 35 kilómetros diarios en el mes de junio, suponiendo días perfectamente soleados. A su favor hay que decir que esta estimación no corresponde a la Costa del Sol: el fabricante Sono Motors está radicado en Múnich (Alemania), y esa es precisamente la ubicación a la que se refieren. Las tablas con el histórico meteorológico de Múnich indican que un mes de junio normal tiene 11 días soleados. Sin embargo; esta información no aparece en la web de Sono Motors.
 Sono Sion. Fuente: Sono Motors
Sono Sion. Fuente: Sono MotorsEstá por ver que estos turismos con apoyo solar —llamarlos coches solares es, a todas luces, engañoso— resulten rentables a largo plazo. La integración de los paneles fotovoltaicos en la carrocería, a pesar de intentar aprovechar las superficies de menor curvatura, resulta compleja y hace una verificación independiente de sus capacidades reales, cuanto menos, difícil. No obstante, sería interesante disponer de una idea de la magnitud del apoyo que puedan proporcionar unos paneles solares en un vehículo electrificado capaz de llevarlos. Para lograr este objetivo, es interesante centrarse en un caso de cálculo particularmente favorable: el camión con apoyo solar. Han aparecido propuestas de camiones electrificados, total o parcialmente, que obtienen cierto apoyo en su autonomía de paneles fotovoltaicos montados sobre las paredes laterales y superior de su zona de carga. Esta disposición permite disponer de grandes espacios, en principio diáfanos, para la instalación de los colectores solares. Espacios que, además, son planos. Se evita de este modo un problema común que aumenta el coste de los paneles en techos u otras superficies de turismos: las curvaturas guiadas por la aerodinámica.
Modelo de cálculo de apoyo solar para camiónPara crear un modelo de cálculo simplificado [3] nos centraremos en un camión con semirremolque de cinco ejes al que dotaremos de paneles fotovoltaicos en los laterales y techo de su semirremolque. El primer paso será calcular las superficies disponibles dadas unas dimensiones típicas.
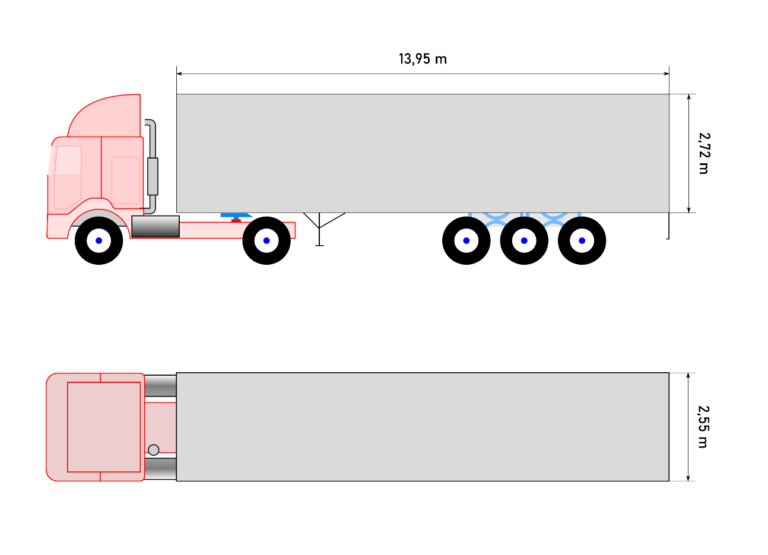 Camión de cinco ejes típico con medidas del semirremolque. Imagen modificada por el autor a partir del diagrama CC BY-SA 3.0 de H Padleckas / Orinoco / Malyszkz, Wikimedia Commons
Camión de cinco ejes típico con medidas del semirremolque. Imagen modificada por el autor a partir del diagrama CC BY-SA 3.0 de H Padleckas / Orinoco / Malyszkz, Wikimedia Commons
A partir de las medidas de la superficie disponible, procedemos a calcular la superficie total expuesta, lo que para un semirremolque típico excede los 110 metros cuadrados. En el siguiente paso, seleccionamos una ubicación y preparamos una consulta a la base de datos PVGIS de la Comisión Europea [4]. Usaremos el cálculo para el sistema más sencillo, el de un panel fotovoltaico conectado a la red, ya que no vamos a tener en cuenta datos de las baterías montadas en el vehículo.
Como quiera que el dimensionamiento de una instalación solar en PVGIS se realiza con su potencia en vatios-pico (los vatios que puede producir una instalación solar fotovoltaica bajo condiciones óptimas de iluminación solar, sin cobertura de nubes y a una temperatura de panel de 25 °C), utilizamos un parámetro común para ligar esta unidad a la superficie unitaria de paneles: un metro cuadrado de panel fotovoltaico ofrece 0,2 kilovatios-pico.
Avanzando en las características del modelo, calcularemos por un lado la energía producida para la ubicación dada por la superficie de paneles del techo de la caja del semirremolque, cuya inclinación, que asumiremos siempre cenital, es fija e igual a cero grados, y su acimut es indiferente. Por otro, tendremos en cuenta un movimiento aleatorio del vehículo a lo largo del año. Computaremos el valor de la energía producida por uno de los laterales, considerando su inclinación como 90 grados y su acimut como una variable aleatoria de distribución uniforme. orientado en cuatro direcciones perpendiculares (–90°, 0°, 90° y 180°, es decir, este, sur, oeste y norte); el resultado será la media aritmética de estos cuatro valores, multiplicada por dos para tener en cuenta ambos lados de la caja.
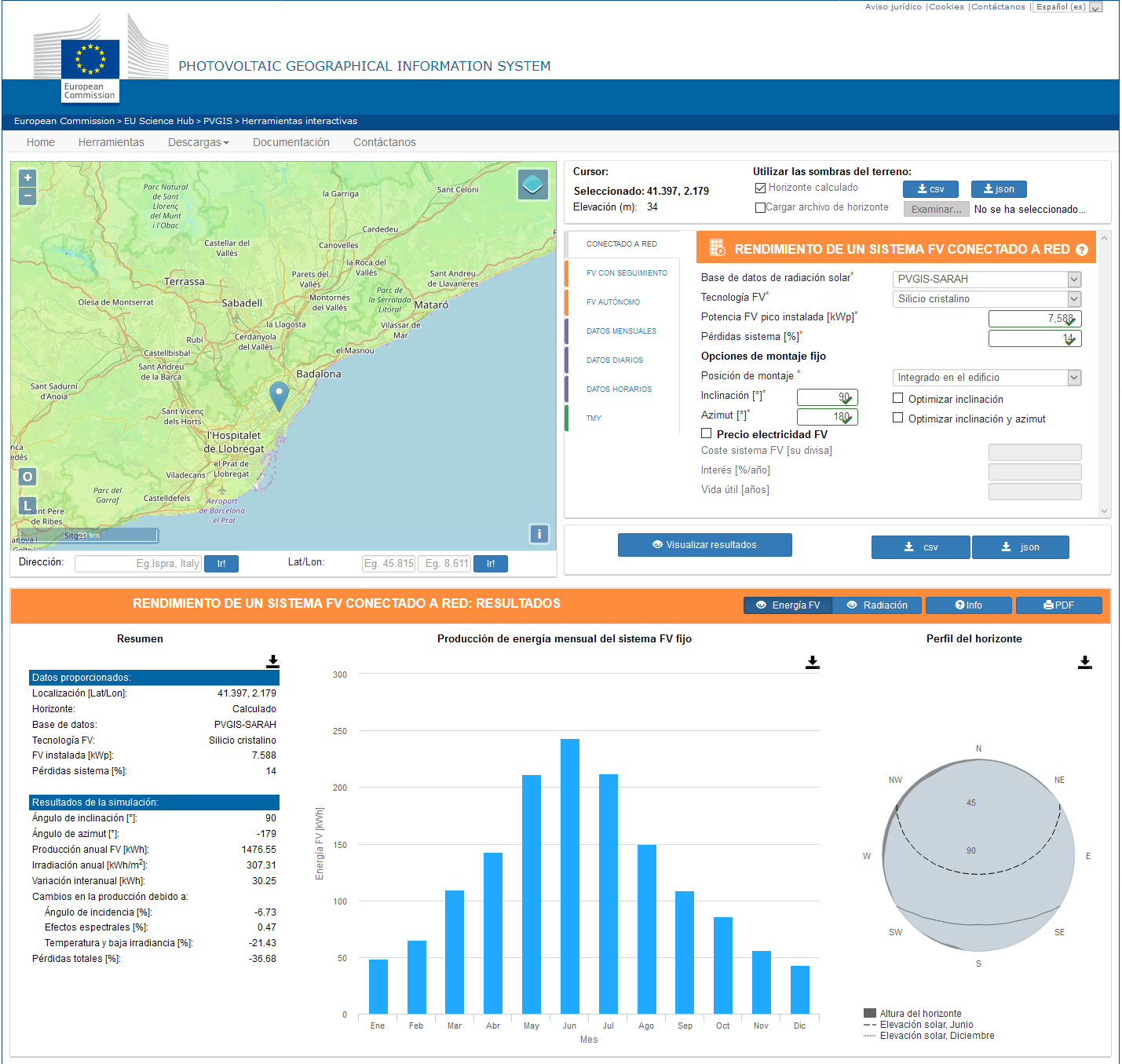 Captura de pantalla de la herramienta PVGIS de la Comisión Europea. Fuente: Comisión Europea
Captura de pantalla de la herramienta PVGIS de la Comisión Europea. Fuente: Comisión EuropeaPara que este valor de energía producida sea correcto, tendremos que imponer la condición de que el camión no visite recintos cerrados ni se encuentre en zonas sombreadas nunca; esto anularía o reduciría significativamente la producción de energía durante el tiempo en el que se viera afectado por esta reducción de la iluminación ambiental. Esta suposición, fácil de hacer para un camión, es mucho más aventurada para un vehículo más pequeño como un turismo. Con todo esto, podemos ya intentar estimar la producción de energía anual del sistema. Los cálculos anuales permiten uniformizar el impacto de la variación día-noche y estacional en la radiación solar incidente.
Estimación del consumo de energía en un camión eléctricoPodemos comprobar que, en el centro de la península Ibérica, instalar paneles fotovoltaicos en las superficies disponibles de un semirremolque de las medidas consideradas permitirá producir más de 19 megavatios-hora en un año. Parece mucho, pero para estar seguros tendremos que comparar esa cifra con cuánta energía consumiría ese mismo camión en su funcionamiento normal, y comprobar que fracción representa la producción solar. ¿El problema? Que, hoy, no existen camiones eléctricos de ese tamaño en producción con los que poder ofrecer cifras fiables. Tanto el Tesla Semi como el Mercedes eActros LongHaul están, según las noticias recientes, a uno y dos años respectivamente de estar disponibles en el mercado.
 Tesla Semi (izquierda) y Mercedes-Benz eActros LongHaul. Fuentes: izquierda, CC BY 2.0 Steve Jurvetson; derecha, MBpassion.de / Philipp Deppe
Tesla Semi (izquierda) y Mercedes-Benz eActros LongHaul. Fuentes: izquierda, CC BY 2.0 Steve Jurvetson; derecha, MBpassion.de / Philipp DeppeSin embargo, sí es posible comparar con el consumo de camiones actuales de motorización térmica, bajo el supuesto de que la energía necesaria para su movimiento será aproximadamente la misma. Un camión del tipo que estamos considerando puede consumir, bajo condiciones de conducción económica y recorridos mayoritariamente sin pendientes, 32 litros de combustible diésel cada cien kilómetros [5]. Este consumo responde al uso total, primario, de energía del camión, pero no nos está dando la información que necesitamos. Hay que ponerlo en términos de energía neta. Para ello, habrá que minorar la parte de la energía que se pierde por las limitaciones termodinámicas de los motores de combustión; con ello tendremos la energía neta que llega finalmente a las ruedas y sistemas auxiliares. Después, imaginaremos que la energía ha sido extraída de una fuente compatible con los paneles solares, de manera que podamos compararla. Por último, añadiremos la parte de pérdidas de un motor eléctrico, que, como veremos, es mucho menos significativa que en el caso del motor de combustión.
Los valores que emplearemos para realizar el cálculo serán:
Densidad energética del combustible diésel: 36,05 MJ/L
En kilovatios-hora/litro: 10,01 kW·h/L
Rendimiento del motor térmico: 45 %
Rendimiento del motor eléctrico equivalente: 90 %
Consideraremos además un kilometraje anual típico de 120000 kilómetros. El camión diésel considerado consumirá 375000 litros de combustible, mientras que un hipotético camión eléctrico equivalente deberá usar del orden de 210 megavatios-hora, arrojando un gasto de energía por kilómetro de 1,75 kilovatios-hora por kilómetro. Como comparación, Tesla afirma que su futuro Tesla Semi tendrá un consumo de 1,24 kilovatios-hora por kilómetro [6], un 29 por ciento menos, lo que es consistente con las diferencias habituales observadas entre consumos declarados y reales en otros vehículos.
Los paneles, según el cálculo de nuestro modelo, ofrecerán algo menos de 20 megavatios-hora, del orden del 9 por ciento de la energía requerida. En términos de distancia, más de 11000 kilómetros «gratuitos». Ahora bien, ¿compensa el montaje? ¿En cuánto tiempo se recuperará la inversión necesaria?
Plazo de retorno de la inversiónEn este momento, sin una disponibilidad real de camiones para modificar, solo es posible hacer estimaciones. La instalación de los paneles fotovoltaicos sobre las superficies de la caja de un semirremolque no se antoja como especialmente compleja, pero es un problema diferente al de un montaje sobre el tejado de un edificio. El sistema no necesitará estar dotado de un inversor, un componente que habitualmente justifica aproximadamente el veinte por ciento del coste de un sistema fotovoltaico de esta magnitud; las baterías de un camión eléctrico almacenan corriente continua. Será necesario, naturalmente, instalar la circuitería necesaria para realizar la adaptación del voltaje de las placas al de las baterías, así como todos los elementos de control necesarios. Al tratarse de una instalación en movimiento, es de prever que los requisitos mecánicos y normativos de seguridad serán más onerosos de cumplir.
Entre factores que disminuyen el precio y otros que lo aumentan, vamos a simplificar considerando que el coste unitario por metro cuadrado de instalación del sistema será similar al disponible hoy para edificios, cuyo límite inferior se encuentra alrededor de los 600 euros. Esto fijaría el coste del sistema fotovoltaico en unos 67000 euros, una magnitud comparable a la de los costes típicos de la cabeza tractora. Una cifra habitual de referencia en las motorizaciones diésel sería 100000 euros, pero con seguridad el coste final será superior para los futuros camiones eléctricos de gran tonelaje). Por su parte, es casi el doble que el coste del propio semirremolque, para el que una cifra típica podría ser 36000 euros.
Ahora estamos en condiciones de calcular un tiempo de retorno de la inversión, si tenemos en cuenta el coste del kilovatio-hora para la carga de las baterías del camión. Considerando un coste de 0,19 euros por kilovatio-hora, no se recuperaría la inversión hasta casi los dieciocho años. La vida media de un camión de gran tonelaje se estima en unos diez años, y aunque es de suponer que las mecánicas más sencillas de las motorizaciones eléctricas conllevarán un aumento considerable del tiempo útil de estos vehículos, dieciocho años parecen un plazo completamente inasumible.
 Gráfico de análisis de coste para camiones de cinco ejes con apoyo solar para una vida máxima del vehículo de 20 años. Fuente: Iván Rivera (elaboración propia)
Gráfico de análisis de coste para camiones de cinco ejes con apoyo solar para una vida máxima del vehículo de 20 años. Fuente: Iván Rivera (elaboración propia)Haciendo un análisis para diferentes escenarios considerando las dos variables clave en esta situación (el coste unitario de instalación de los paneles fotovoltaicos y el coste por kilovatio-hora de la energía de recarga, encontramos que, si establecemos de forma muy conservadora los diez años como el periodo mínimo de retorno aceptable para la inversión de instalar paneles fotovoltaicos en el semirremolque, encontramos que los costes de instalación unitarios deben disminuir hasta los 500 euros por metro cuadrado y el precio medio de la energía aumentar hasta los 0,3 euros por kilovatio-hora. Para costes de instalación unitarios más bajos, el precio medio de la energía aceptable en todo el periodo disminuye también. Para un valor similar al considerado inicialmente de 0,19 euros por kilovatio-hora, el coste unitario de instalación tendría que bajar a la mitad (300 euros por metro cuadrado) para que el tiempo de retorno bajara de los nueve años.
De modo un tanto alarmante, el precio por metro cuadrado del panel fotovoltaico, que ha mostrado un comportamiento histórico de disminución exponencial hasta 2019 [7], parece haberse estabilizado e incluso aumentado en los últimos tres años [8], a pesar del crecimiento constante en su capacidad productiva en todo el mundo.
El futuro del camión con apoyo fotovoltaicoEn conclusión: no vemos paneles solares en camiones por un conjunto de razones. Para empezar, los camiones tienen que evolucionar en motorización: sin al menos una motorización híbrida con una capacidad suficiente de baterías, no tiene sentido la instalación de placas fotovoltaicas salvo para alimentar sistemas secundarios (la refrigeración aparece aquí como una oportunidad a considerar). Por otro lado, es necesario que el coste de las instalaciones fotovoltaicas disminuya de forma clara, algo que podría suceder aún pese al comportamiento reciente del mercado, achacable al menos en parte a las turbulencias logísticas inducidas por la crisis de la COVID-19. Y, por último, este tipo de instalaciones tienen más sentido cuanto mayor sea el coste del kilovatio-hora para la recarga. Lamentablemente, todas las señales apuntan en este sentido a corto y medio plazo.
El caso de negocio para empresas del tipo de Sono Motors, que ha propuesto adaptaciones para camiones de este estilo [9], está en el aire. Y esto, sin responder a una pregunta más: ¿aceptarán los operadores de camiones ceder el espacio de los laterales de los semirremolques para un fin diferente a anunciarse en letras de dos metros de altura?
Bibliografía[1] Lightyear. (2022). Long Range Solar Electric Vehicle – Lightyear 0. Visitado el 29/09/2022 en
[2] Sono Motors. (2022). The Sion – the car that charges itself. Visitado el 29/09/2022.
[3] Rivera, I. (29/09/2022). Modelo de cálculo de apoyo solar para camiones. Google Spreadsheets.
[4] Comisión Europea. (01/03/2022). PVGIS Photovoltaic Geographical Information System. EU Science Hub. Visitado el 29/09/2022.
[5] Instituto para la Diversificación y el Ahorro de Energía. (2009). Guía para la gestión del combustible en las flotas de transporte por carretera. Centro de Publicaciones, Ministerio de Fomento. Visitado el 29/09/2022.
[6] García, G. (15/02/2021). Ya sabemos la capacidad del tesla semi: 500 KWH, ¿Escasa para un camión eléctrico? Híbridos y Eléctricos. Visitado el 29/09/2022.
[7] Oxford Martin School, University of Oxford. (2020). Solar PV module prices. Our World in Data. Visitado el 29/09/2022.
[8] Gifford, J. (04/01/2022). Higher PV module prices may point to stable demand and more sustainable pricing trends. PV Magazine International. Visitado el 29/09//2022.
[9] Sono Motors. (08/09/2022). Sono Motors presents financial results for the second quarter of 2022. Sono Motors. Visitado el 29/09//2022.
Sobre el autor: Iván Rivera es ingeniero especializado en proyectos de innovación de productos y servicios para ferrocarriles.
El artículo El camión solar: ¿una posibilidad real? se ha escrito en Cuaderno de Cultura Científica.
El problema del recorrido del caballo en el tablero de ajedrez (II)
En la anterior entrada del Cuaderno de Cultura Científica titulada El problema del recorrido del caballo en el tablero de ajedrez, iniciamos una pequeña serie sobre este clásico problema en el que se relacionan ajedrez y matemáticas, el problema de recorrer todas las casillas de un tablero de ajedrez con la figura del caballo, pasando una vez y sólo una vez por cada casilla. En particular, en esa entrada centramos nuestra atención en la cuestión de la existencia de solución al problema para tableros rectangulares de tamaño n x m, mientras que en esta entrada nos centraremos en la cuestión de cómo construir esos recorridos.
 El reino del ajedrez (2008), del artista mexicano Carlos Orduña Barrera. Imagen de su página web: Carlos Orduña BarreraEl problema del recorrido del caballo
El reino del ajedrez (2008), del artista mexicano Carlos Orduña Barrera. Imagen de su página web: Carlos Orduña BarreraEl problema del recorrido del caballo
Empecemos recordando exactamente qué nos plantea este juego o problema.
Problema del recorrido del caballo: Buscar un recorrido de la figura del caballo sobre el tablero de ajedrez que consista en mover esta pieza, desde una casilla inicial, de forma sucesiva a través de todas las casillas del tablero, pasando una sola vez por cada una de ellas, y terminando en la casilla inicial.
Aunque el juego del recorrido del caballo se plantea sobre el tablero clásico, de tamaño 8 x 8, desde el inicio se interesaron en la solución para tableros cuadrados de diferentes tamaños n x n, para tableros rectangulares de tamaño n x m, e incluso, para tableros de formas diversas.
Por otra parte, se distinguieron dos tipos de soluciones. Los recorridos como el planteado en el enunciado anterior, que se denomina recorrido cerrado, ya que empieza y acaba en la misma casilla, aunque se puede plantear la variante del problema que consiste en que las casillas inicial y final no sean las mismas, en cuyo caso se habla de recorrido abierto.
En la entrada anterior, como comentábamos, dedicamos nuestra atención al problema de la existencia de recorridos (abiertos y cerrados) sobre un tablero rectangular. Analizamos con un poco más de detalle los tableros de tamaño 3 x m (dejamos abierto el problema 3 x 4 que resolveremos en otra entrada de esta serie), así como el tablero 4 x 4, y recordamos cual era el resultado general: para un tablero n x m, con n menor o igual que m, existen recorridos de caballos cerrados si no se da alguno de los casos siguientes: i) n y m impares; ii) n = 1, 2 o 4; iii) n = 3 y m = 4, 6 o 8.
En esta entrada se van a analizar algunos métodos clásicos de construcción de recorridos del caballo sobre el tablero de ajedrez.
El método de los matemáticos De Moivre y De MontmortEl matemático y abogado británico Walter William Rouse Ball (1850-1925) menciona en su libro Recreaciones matemáticas y ensayos (1892) que el primer método, del que él tiene conocimiento, para obtener recorridos del caballo sobre el tablero de ajedrez, es de los matemáticos franceses Abraham de Moivre (1667-1754) y Pierre Rémond de Montmort (1678-1719).
Este método consiste en dividir el tablero en dos partes, un anillo exterior de una anchura de dos celdas y un cuadrado interior 4×4, de forma que primero se recorra con el caballo la zona exterior, solo entrando en la zona interior si es completamente necesario, y después de recorrer el anillo exterior, continuar con el trayecto por la parte interior.
 Zonas interior –verde– y exterior –azul– del tablero de ajedrez para el método de De Moivre y De Montmort
Zonas interior –verde– y exterior –azul– del tablero de ajedrez para el método de De Moivre y De Montmort
Podemos empezar a buscar un itinerario del caballo empezando en una esquina del tablero y recorriendo el anillo exterior de forma circular, por ejemplo, en el sentido de las agujas del reloj (véase la siguiente imagen), de forma que se van saltando las casillas que hemos numerado 1, 2, 3, así hasta la casilla 24, desde la cual no podemos seguir saltando a una casilla de la zona exterior (véase la siguiente imagen).
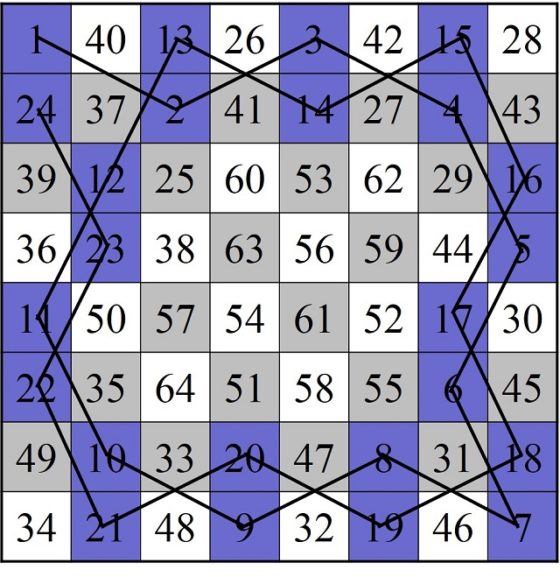
Como en la casilla 24 nos hemos bloqueado en nuestro recorrido por el anillo exterior, hay que apoyarse en la zona interior (casilla 25) para poder continuar el trayecto por el anillo exterior. Así seguimos saltando hasta la casilla 37, en la que nos volvemos a bloquear, y hay que volver a entrar puntualmente en la zona interior para poder seguir. El recorrido por el anillo exterior se termina en la casilla 50 (véase la siguiente imagen).
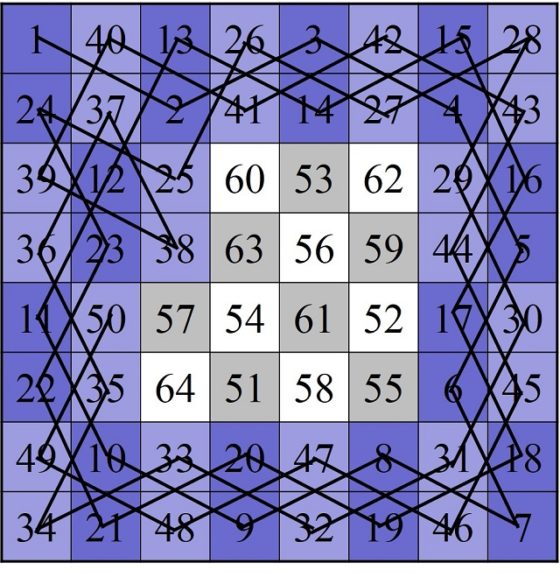
Para terminar el recorrido del caballo solo queda saltar por las casillas de la zona interior. Al empezar en la casilla de la esquina es imposible alcanzar esa esquina desde la zona interior, luego el recorrido será abierto. En la imagen siguiente se muestra el final del mismo.

Por el comentario anterior, las esquinas no se conectan con la zona interior, para conseguir un camino cerrado con la técnica de De Moivre y De Montmort habría que empezar en una casilla desde la que sí se pueda acceder desde la zona exterior. Una pequeña diversión para las personas que estáis leyendo esta entrada podría ser analizar cómo construir recorridos del caballo utilizando la técnica aprendida de los matemáticos franceses del siglo XVIII, empezando en diferentes casillas del anillo exterior, y ver si en algunos casos se pueden conseguir recorridos cerrados o modificar los recorridos abiertos obtenidos para convertirlos en cerrados.
A continuación, se muestra un camino cerrado partiendo de una casilla de una de las diagonales principales del tablero, que no está en ninguna esquina del mismo, y que está en el anillo exterior.
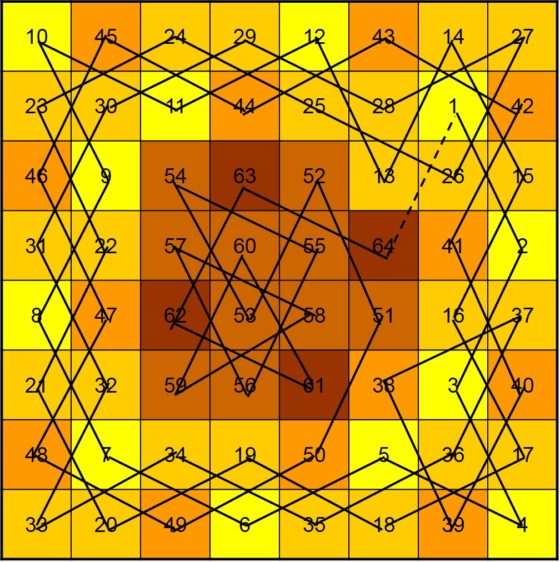
Aunque nos estamos refiriendo a la técnica de De Moivre y De Montmort para resolver el problema del recorrido del caballo sobre el tablero de ajedrez, lo cierto es que esta técnica aparece ya varios siglos antes. El pedagogo, inspector de educación e historiador del ajedrez británico Harold J. R. Murray (1868.1955) en su libro Historia del ajedrez muestra un recorrido abierto de un ajedrecista árabe desconocido, del que se sabe que se llamaba Ali Ibn Mani, que es esencialmente la misma solución que hemos mostrado al describir el método de los matemáticos franceses. Aunque el problema es datar dicha construcción ya que aparece recogida en un manuscrito, de alrededor del año 1350, sobre ajedrez de Abu Zakariya Yahya ben Ibrahim al-Hakim, titulado El deleite de los inteligentes, una descripción del ajedrez, y que también recoge el primer recorrido cerrado de Al-Adli (hacia el 840), que se comenta en la anterior entrada.
El método del matemático Leonhard EulerEl matemático suizo Leonhard Euler (1707-1783) fue el primero en realizar un análisis matemático riguroso del juego del recorrido del caballo en su artículo Solución a una cuestión ingeniosa que parece que no ha sido analizada (Memoria de la Academia de Ciencias de Berlín, escrito en 1759 y publicado en 1766).
 Las dos primeras páginas del artículo de Leonhard Euler Solución a una cuestión ingeniosa que parece que no ha sido analizada (1759)
Las dos primeras páginas del artículo de Leonhard Euler Solución a una cuestión ingeniosa que parece que no ha sido analizada (1759)
En particular, en este artículo desarrolló el siguiente método para obtener recorridos cerrados. Esta técnica consistía en buscar de forma aleatoria un recorrido del caballo sobre el tablero de ajedrez lo más largo posible, que dejara una cantidad pequeña de casillas sin recorrer, para después intercalar estas casillas en diferentes partes del mismo con el objetivo de construir un recorrido cerrado que cubra todas las casillas del tablero.
A continuación, mostramos el ejemplo que aparece en el libro Recreaciones matemáticas y ensayos (1892), de W. W. Rouse Ball, que según se menciona es un ejemplo que el matemático francés Adrien-Marie Legendre (1752-1833) considera especialmente difícil. Supongamos que, en esa búsqueda aleatoria de una solución del problema, se ha construido un recorrido que consta de 60 casillas, que nombramos 1, 2, 3, …, 59, 60, como estamos haciendo a lo largo de estas entradas, y se han dejado fuera cuatro casillas, que nombramos A, B, C y D, que son las que aparecen en la siguiente imagen (en negrita los números inicial y final del camino abierto y en rojo los de las casillas por las que no se ha pasado).
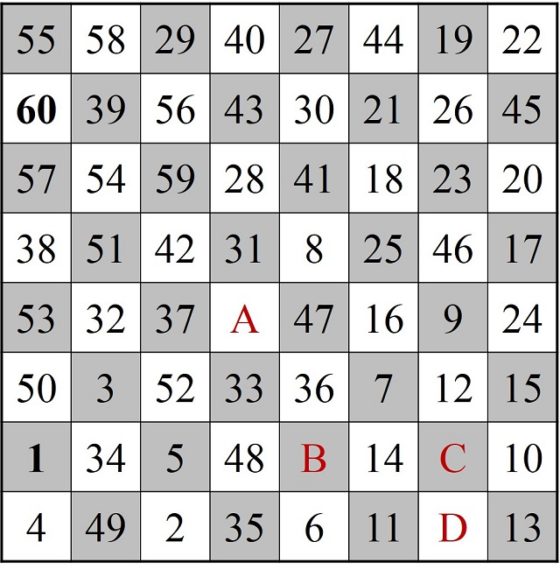
Lo primero que se hace es intentar cerrar el recorrido, aunque no tenga las 64 casillas. Nos fijamos entonces en la casilla 1 (la primera del recorrido), que es “adyacente” a las casillas numeradas como 2, 32 y 52, es decir, se llega a ellas con el salto del caballo desde la casilla 1, y en la casilla 60 (la última del recorrido), que es adyacente a 29, 51 y 59. Como las casillas 51 (cercana a la casilla 60) y 52 (cercana a la casilla 1) son adyacentes entre sí, vamos a poder construir un recorrido cerrado. Veamos cómo hacerlo.
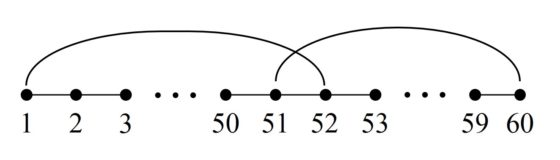 Sencilla representación del recorrido del caballo desde la casilla 1 a la 60, junto con las dos adyacencias comentadas de la casilla 51, con la 60, y la casilla 52, con la 1
Sencilla representación del recorrido del caballo desde la casilla 1 a la 60, junto con las dos adyacencias comentadas de la casilla 51, con la 60, y la casilla 52, con la 1
Entonces, podemos determinar un recorrido cerrado que consiste en saltar por las casillas desde la 1 hasta la 51, de esta saltar a la 60, y seguir en orden inverso, desde la 60 hasta la casilla 52, que es adyacente a la casilla 1, cerrando así el paseo. Para que nuestro recorrido siga en orden, podemos renombrar las celdas 60, 59, 58, …, 53, 52 como 52, 53, … 58, 59, 60, es decir, en orden inverso. Si hacemos esto el recorrido que nos queda es el que aparece en la siguiente imagen y como vemos es un itinerario cerrado del 1 al 60, que aún no incluye las cuatro casillas A, B, C y D.
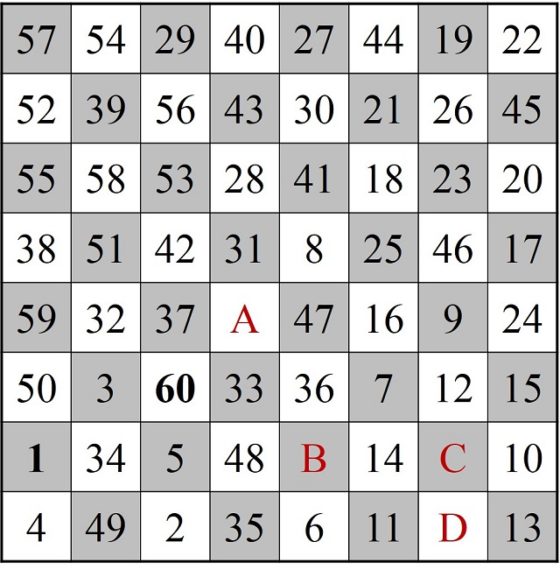
Ahora se trata de ver cómo añadir las casillas no recorridas. Las casillas A, B y D están conectadas mediante el salto del caballo, luego se trata de crear un nuevo recorrido abierto a partir de la ruta cerrada 1–60, que además incluya a A, B y D. Como resulta que la casilla A está conectada con las casillas 3, 5, 7, 25, 41, 51 y 53, podemos conectar la casilla 51 con las casillas A, B y C, y tendremos el recorrido abierto 52, 53, …., 60, 1, 2, …, 50, 51, A, B, C.
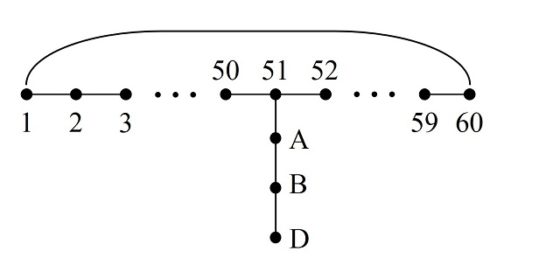 Sencilla representación del recorrido cerrado del caballo desde la casilla 1 a la 60, junto con el recorrido A-B-D adyacente a la casilla 51
Sencilla representación del recorrido cerrado del caballo desde la casilla 1 a la 60, junto con el recorrido A-B-D adyacente a la casilla 51
Ahora, para mantener nuestro recorrido (abierto) de 63 casillas en orden, vamos a renombrar las casillas 52, 53, …., 60, 1, 2, …, 50, 51, A, B, C, como 1, 2, 3, …, 59, 60, 61, 62, 63, como aparece en la siguiente imagen.
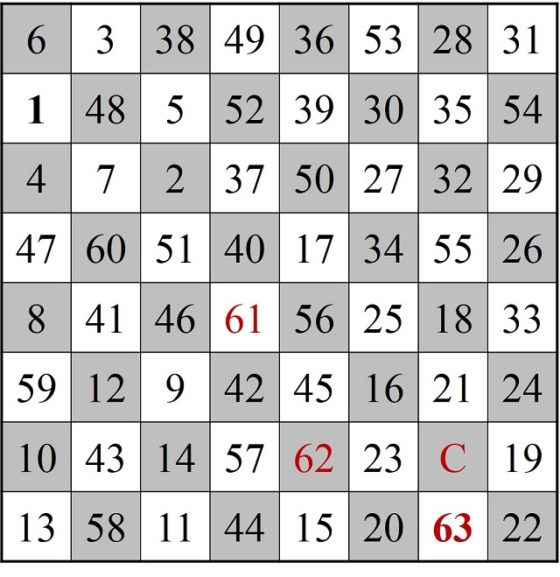
Por lo tanto, tenemos un recorrido abierto que va de la casilla 1 a la 63 y queda por saltar por la casilla C y cerrar el camino. Como resulta que C es adyacente a 25 y 63 es adyacente a 24, vamos a poder intercalar la casilla C consiguiendo así un recorrido abierto con las 64 casillas del tablero
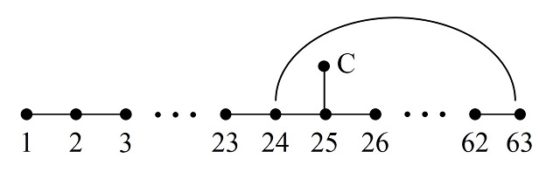 Sencilla representación del recorrido abierto del caballo desde la casilla 1 a la 63, con las adyacencias de la casilla C con la 25 y la casilla 24 con la 63
Sencilla representación del recorrido abierto del caballo desde la casilla 1 a la 63, con las adyacencias de la casilla C con la 25 y la casilla 24 con la 63
Por lo tanto, el recorrido buscado empezaría en la casilla 1 e iría saltando hasta llegar a la casilla 24, de ahí se saltaría a la 63 y se iría saltando hacia atrás hasta la 25, de la cual se pasaría a la casilla C. Y de nuevo renombramos las casillas 1, 2, 3, …, 23, 24, 63, 62, …, 26, 25, C, para que quede el recorrido abierto del 1 al 64, como aparece en la siguiente imagen.
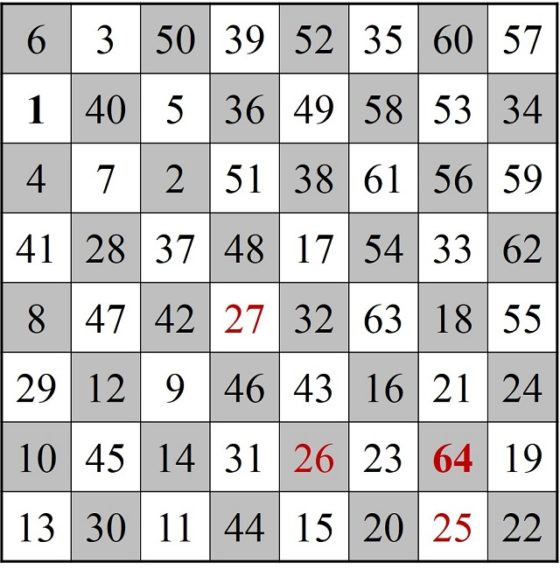
Ahora ya solo nos queda cerrar el recorrido, pero resulta que las casillas inicial (1) y final (64) están bastante alejadas la una de la otra, lo que dificulta poder realizar el cierre. Por lo tanto, Euler modifica el recorrido abierto por obtener otro que tenga las casillas inicial y final más cercanas. Para ello, Euler elige una celda que sea adyacente con la celda 1, en concreto, la celda 28, y que es adyacente a la celda 27, la cual está más cerca de la casilla 64.
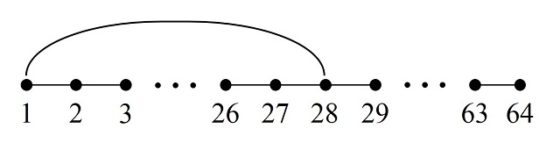 Sencilla representación del recorrido abierto del caballo desde la casilla 1 a la 64, con la adyacencia de la casilla 1 con la 28
Sencilla representación del recorrido abierto del caballo desde la casilla 1 a la 64, con la adyacencia de la casilla 1 con la 28
Entonces, se considera el recorrido abierto que empieza en la casilla 27, va hacia atrás hasta la casilla 1, de donde salta a la 28 y sigue hasta la 64. Así tenemos un itinerario abierto, con el inicio y el final más próximos, pero antes renombremos nuestras casillas 27, 26, … 2, 1, 28, 29, …, 64 como 1, 2, 3, …, 61, 62, 63, 64 (imagen siguiente).
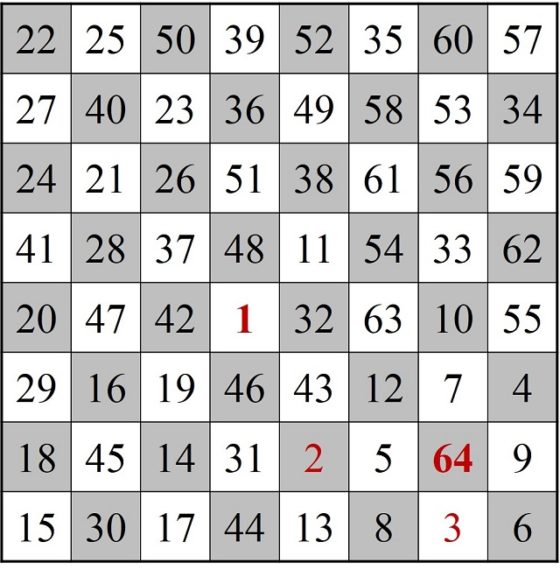
Finalmente vamos a poder cerrar el recorrido abierto, ya que las casillas inicial y final, ahora sí, están cercanas. Por ejemplo, la casilla inicial (1) es adyacente a la casilla 14, mientras que la casilla final (64) es adyacente a la casilla 13, y podemos hacer la misma jugada que hicimos al cerrar el primer camino.
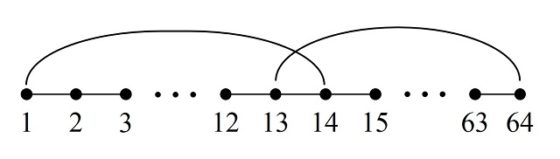 Sencilla representación del recorrido abierto del caballo desde la casilla 1 a la 64, junto con las dos adyacencias comentadas de la casilla 1, con la 14, y la casilla 64, con la 13
Sencilla representación del recorrido abierto del caballo desde la casilla 1 a la 64, junto con las dos adyacencias comentadas de la casilla 1, con la 14, y la casilla 64, con la 13
De la misma manera que al principio de la descripción de esta técnica, el recorrido cerrado será empezar con el 13 e ir saltando en sentido inverso hasta 1, de ahí saltar a la casilla 14 y seguir saltando hasta la casilla 64 (que cierra con la casilla 13). Solo nos falta renombrar el recorrido 13, 12, …, 2, 1, 14, 15, …, 64 como 1, 2, …, 63, 64, como vemos en la siguiente imagen.
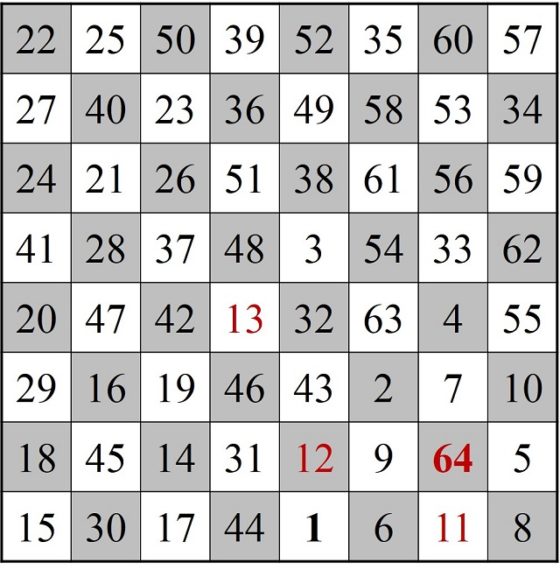 Recorrido cerrado del caballo por el tablero de ajedrez, obtenido mediante la técnica de Euler
Recorrido cerrado del caballo por el tablero de ajedrez, obtenido mediante la técnica de EulerLa técnica de H. C. von Warnsdorff
El alemán H. C. von Warnsdorff propuso un método sencillo y elegante de resolver el problema del recorrido del caballo, en su publicación titulada La solución más sencilla y general al salto del caballo (1823), que podéis encontrar en internet.
La técnica de H. C. von Warnsdorff para encontrar recorridos del caballo sobre el tablero 8 x 8 es la siguiente: Mueve el caballo a una casilla adyacente (es decir, a la que se llegue con el movimiento del caballo), que no haya sido visitada ya y que tenga el menor número de casillas adyacentes libres. Si se da un empate, elegir de forma arbitraria.
Esta es una regla intuitiva, puesto que indica que hay que visitar primero las casillas con menos conexiones, que son aquellas que si no se recorren en ese momento quizás, por la falta de conexiones, no se pueda regresar después a pasar por ellas, que realmente se puede utilizar para todo tipo de tableros rectangulares, que es bastante eficaz a la hora de buscar algunos recorridos particulares del caballo, aunque no es válida para una búsqueda exhaustiva, por ejemplo, los recorridos anteriores de Euler o Al-Adli sobre el tablero clásico no verifican la regla de von Warnsdorff.
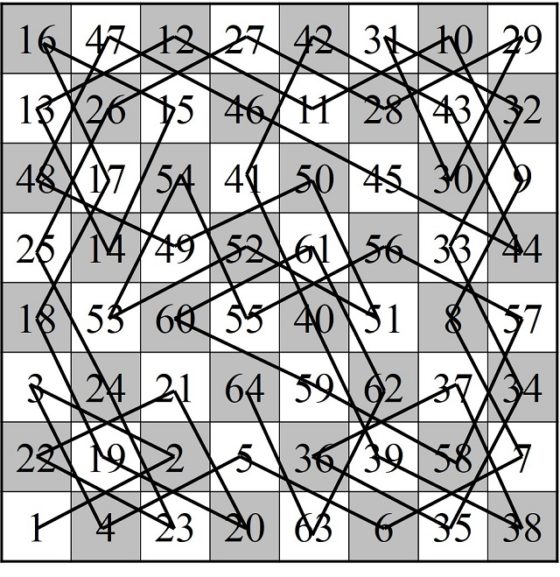 Recorrido del caballo sobre un tablero 8 x 8 obtenido mediante el método de von Warnsdorff
Recorrido del caballo sobre un tablero 8 x 8 obtenido mediante el método de von Warnsdorff
Sin embargo, el método no resuelve bien los casos en los que hay empates en el número de casillas adyacentes libres. Si se elige al azar la casilla en la que continuar, como sugiere Warnsdorff, puede ocurrir que el recorrido se pare en un momento intermedio y no pase por todas las casillas del tablero, como se muestra en el siguiente ejemplo 5 x 5.
Si utilizamos la regla de Warnsdorff para un tablero 5 x 5, empezando en la casilla del medio de la primera fila, el primer empate se produce al llegar a la casilla 9, que tiene dos opciones de continuidad, dos casillas con número de casillas adyacentes libres igual a 2, en el lateral y debajo de la casilla número 5.
 Inicio de un recorrido construido con la técnica de von Warnsdorff, donde se indica con números rojos grandes las casillas recorridas, del 1 al 9, y con números pequeños negros las casillas libres conectadas con dicha casilla mediante el salto del caballo
Inicio de un recorrido construido con la técnica de von Warnsdorff, donde se indica con números rojos grandes las casillas recorridas, del 1 al 9, y con números pequeños negros las casillas libres conectadas con dicha casilla mediante el salto del caballo
Si se continúa con la casilla lateral, el recorrido se estanca después de la casilla 16, como se muestra en la siguiente imagen, puesto que si el caballo salta a la esquina de abajo a la izquierda (como indicaría la regla), ya no puede salir, pero si continuase por otra casilla, no volvería nunca a esa casilla que tiene 0 casillas adyacentes libres.
 Inicio de un recorrido construido con la técnica de von Warnsdorff que se ha bloqueado en la casilla 16
Inicio de un recorrido construido con la técnica de von Warnsdorff que se ha bloqueado en la casilla 16
Sin embargo, si se continúa, tras el empate, con la casilla de debajo de la 5, existen varias soluciones continuando con la regla, una de ellas la mostrada en la imagen.
 Recorrido final construido con la técnica de von Warnsdorff
Recorrido final construido con la técnica de von Warnsdorff
Puede verse en la literatura sobre el tema, que diferentes autores han modificado la regla de Warndorff mediante el diseño de métodos para determinar la mejor elección de una casilla cuando se produce un empate. El más sencillo de los cuales consiste en la elección, en caso de empate, de la casilla más alejada (con la distancia euclídea) al centro del tablero, que es el método que yo he utilizado para deshacer los empates en el recorrido mostrado anteriormente sobre el tablero 8 x 8.
La construcción de RogetVamos a terminar esta entrada con el método que propuso el médico, matemático, físico, teólogo y lexicólogo británico Peter Mark Roget (1779-1869), en un artículo de la revista Philosophical Magazine en 1840.
Roget divide el tablero 8 x 8 en cuatro zonas, cada una de ellas formada por un cuadrado 4 x 4, y las 16 casillas de cada cuarto de tablero las separa en cuatro grupos de 4 casillas, que forman un recorrido cerrado sobre esa zona 4 x 4. A cada una de las casillas de esos grupos, o recorridos cerrados, las nombra con una misma letra L, E, A, P (la palabra leap, en inglés, significa “salto”). Los recorridos de las letras L y P tienen forma de diamante, mientras que los de las letras A y E de cuadrado.
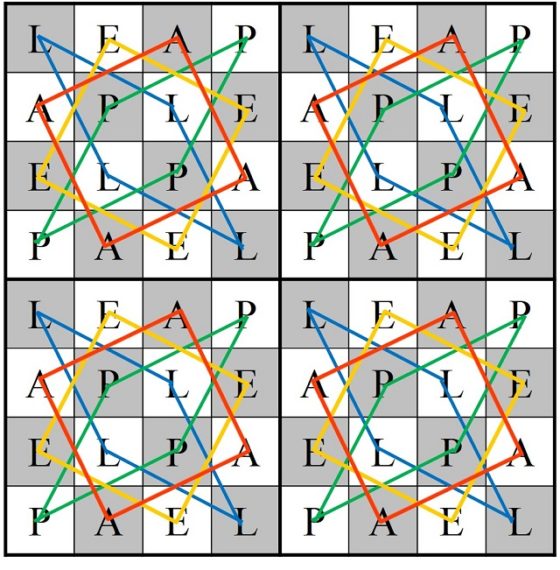
Entonces, Roget considera movimientos del caballo que son de tipo LL, EE, AA, PP (de una casilla de una letra a otra de la misma letra) y movimientos de tipo EL, AL, EP, AP (de una casilla con una letra vocal a una casilla con una letra consonante, o viceversa), como se muestra en las siguientes imágenes.
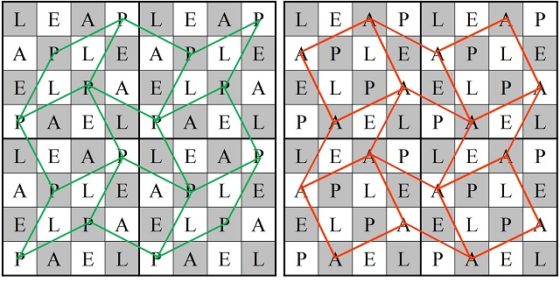 Movimientos de tipo LL y AA sobre el tablero de ajedrez
Movimientos de tipo LL y AA sobre el tablero de ajedrez
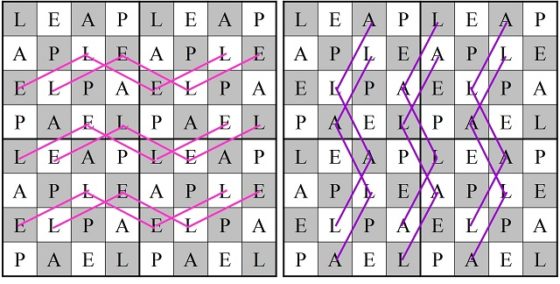 Movimientos de tipo EL y AL sobre el tablero de ajedrez
Movimientos de tipo EL y AL sobre el tablero de ajedrez
Con las 16 casillas de cada una de las letras se puede construir un circuito cerrado, luego disponemos de cuatro tipos de circuitos cerrados con 16 casillas, cada uno con cada una de las letras. Ahora para construir el recorrido de las 64 casillas se combinan cuatro circuitos de una sola letra de forma que después de un circuito de una vocal va uno de una consonante, y viceversa. En el siguiente ejemplo, hemos empezado con el circuito de la letra P, después el circuito de la letra A, luego L y finalmente E, creando un recorrido abierto.
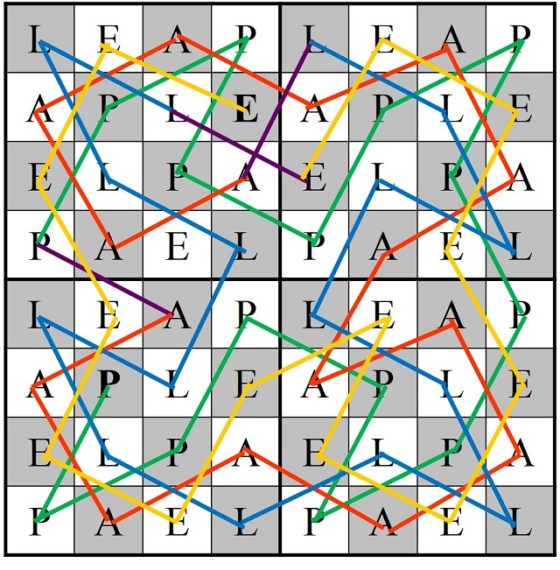 Recorrido abierto del caballo sobre el tablero de ajedrez realizado con la técnica de Roget
Recorrido abierto del caballo sobre el tablero de ajedrez realizado con la técnica de Roget
Y no podía faltar un poco de arte para terminar la entrada.
 Caballo negro (2006), del artista mexicano Carlos Orduña Barrera. Imagen de su página web: Carlos Orduña Barrera
Caballo negro (2006), del artista mexicano Carlos Orduña Barrera. Imagen de su página web: Carlos Orduña Barrera
Bibliografía:
1.- Raúl Ibáñez, Del ajedrez a los grafos, la seriedad matemática de los juegos, El mundo es matemático, RBA, 2015.
2.- Édouard Lucas, Recreaciones Matemáticas, vol. 1 – 4, Nivola, 2007, 2008.
3.- Miodrag S. Petrovic, Famous Puzzles of Great Mathematicians, AMS, 2009.
4.- Harold J. R. Murray, A History of Chess (Historia del ajedrez), Oxford University Press, 1913.
5.- W. W. Rouse Ball, H. S. M. Coxeter, Mathematical Recreations and Essays, Dover Publications, 1987 (originalmente publicada por W. W. R. Ball en 1892 –la versión original puede encontrarse en el Proyecto Gutenberg – y extendida por el geómetra H. S. M. Coxeter en 1974)
6.- John J. Watkins, Across the Board: The Mathematics of Chessboard Problems, Princeton University Press, 2004.
7.- H. C. von Warnsdorf, Des Rösselsprunges einfachste und allgemeinste Lösung, Verhagen, 1823.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo El problema del recorrido del caballo en el tablero de ajedrez (II) se ha escrito en Cuaderno de Cultura Científica.
Einstein y Newton
En el siglo XVII Isaac Newton básicamente creó la física del mundo moderno, desarrollando modelos acerca de la gravedad, la luz, la inercia, la masa, e incluso las matemáticas necesarias para comprender estos conceptos. La mecánica de Newton fue considerada como la descripción definitiva del universo, hasta que Einstein vino a cambiarlo todo.
 Newton / Einstein Proxxi Composite (2003) de Daniel Rozin. Para ver correctamente la imagen debes tener en cuenta que la realidad depende del observador: aléjate de la pantalla (o minimiza el tamaño) hasta que veas a Newton; acércate (o aumenta el tamaño) para ver a Einstein. Fuente: Daniel Rozin / smoothware.com
Newton / Einstein Proxxi Composite (2003) de Daniel Rozin. Para ver correctamente la imagen debes tener en cuenta que la realidad depende del observador: aléjate de la pantalla (o minimiza el tamaño) hasta que veas a Newton; acércate (o aumenta el tamaño) para ver a Einstein. Fuente: Daniel Rozin / smoothware.comEinstein fue el que comenzó la revolución de la física moderna que terminaría derrocando el viejo paradigma de la física newtoniana, por lo que tanto Einstein como Newton crearon las bases de nuevas formas de pensar. Efectivamente, hay grandes paralelismos entre ambos físicos. Los dos tuvieron lo que ha dado en llamarse un “año maravilloso” cuando tenían veintitantos años. El de Newton fue el que él llamó “año de la plaga”, en 1666. Ese año creó el cálculo diferencial e integral, descubrió la ley de gravitación universal y determinó cómo la gravedad hace que los planetas se muevan en elipses. El de Einstein fue en 1905, durante el que publicó la teoría especial de la relatividad, la solución al problema del efecto fotoeléctrico (para la que aplicó la hipótesis cuántica a la luz), una explicación del movimiento browniano y la ecuación E = mc2.
Hay, sin embargo, una pequeña diferencia entre Einstein y Newton a la hora de tratar estos descubrimientos: Newton no publicó la mayoría de sus primeros trabajos hasta décadas después pero, cuando lo hizo, todo el mundo los aclamó como correctos inmediatamente. Los dos hombres también están unidos por el hecho de que ambos llegaron a ser tremendamente famosos durante sus vidas. Newton fue una figura tan iconográfica durante su época como Einstein lo fue en la suya, solo hay que sustituir una formal peluca británica por la melena alborotada de Einstein.
A lo largo de los siglos, la fama de Newton como fundador de la física moderna le había incrustado en la consciencia de la sociedad como el genio que había creado la ciencia tal y como se conocía. Surgieron, sin embargo, varias discrepancias, las más evidentes tenían que ver con la luz y la óptica.
Newton había lanzado la hipótesis de que la luz estaba constituida por “corpúsculos”, partículas como pequeñas bolas. En el siglo XIX varios físicos, entre ellos, más notablemente, James Clerk Maxwell, habían determinado que la luz era de hecho una onda. Pero los problemas para la mecánica newtoniana estaban solo comenzando. La teoría de Maxwell cuestionaba otras facetas de la visión del mundo de Newton. Para la época en que Einstein estaba haciendo el doctorado estaba claro para los físicos más perceptivos de que se estaba en medio de una crisis: o Newton estaba equivocado o lo estaba Maxwell. La publicación por Einstein en 1905 de la teoría especial de la relatividad fue el golpe decisivo: Maxwell era el ganador y la mecánica newtoniana, con su dependencia del tiempo y del espacio absolutos, era incorrecta. Pero Einstein no se paró ahí. Si bien no tenía un plan premeditado para desmantelar el edificio que Newton había construido, él fue el que vino a cambiar el concepto aceptado, mecánico y determinista, del mundo.
Einstein abordó la cuestión de la gravedad, dándose cuenta de que la forma en la que era comprendida no era compatible con su teoría de la relatividad. En 1911 publicaría su primera aproximación a la teoría general de la relatividad, que reformaba otra de las grandes teorías de newton: la ley de la gravedad universal. Newton había dicho que todos los objetos del universo se atraían entre sí con una fuerza proporcional a sus masas. Pero sabía que no podía ofrecer una idea de por qué esto era así. “Non fingo hypotheses”, no formulo hipótesis, fue su comentario ante su falta de una teoría. Con la relatividad general Einstein ofrecía una solución a por qué la gravedad funcionaba: dos objetos se atraían entre sí porque la masa distorsiona el espaciotiempo alrededor de ella de tal manera que cualquier otra masa en su cercanía se “desliza” hacia ella. En su forma más sencilla las ecuaciones de Einstein son equivalentes a las de Newton; las de Newton no son expresiones equivocadas, sino incompletas, y las de Einstein son más completas. Algún día aparecerá una teoría que complete aún más las de Einstein.
A pesar de haber contribuido tanto a bajar del pedestal en el que se encontraban las ideas de Newton, Einstein siempre profesó una gran admiración por el inglés. En 1940, en un artículo que escribió para Science titulado “Consideraciones acerca de los fundamentos de la física teórica”, Einstein dijo de Newton que fue la primera persona en “establecer una base teórica uniforme” para el mundo de la ciencia. Einstein seguía: “Esta base newtoniana probó ser sumamente fructífera y fue considerada definitiva hasta finales del siglo XIX. No solamente proporcionó resultados para los movimientos de los cuerpos celestes, hasta los más pequeños detalles, sino que también suministró una teoría de la mecánica de las masas continuas y discretas, una explicación sencilla del principio de conservación de la energía y una teoría completa y brillante del calor”. Newton había producido un conjunto de reglas, sistemático y omnicomprensivo, que unía todos los fenómenos conocidos en su época. Encontró que la mecánica era una forma tan buena de explicar la naturaleza que la aplicó a todo lo que vio; como lo hizo todo el mundo los doscientos años siguientes, hasta que llegó Einstein para cambiar de nuevo la visión del mundo.
Referencia:
Einstein, A. (1940). Cnsiderations concerning the fundaments of theoretical physics Science, 91 (2369), 487-492 DOI: 10.1126/science.91.2369.487
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
Una versión anterior de este artículo se publicó en Experientia Docet el 6 de junio de 2010.
El artículo Einstein y Newton se ha escrito en Cuaderno de Cultura Científica.

