Números errores de impresión
Cuando hace un año escribí la entrada ¿Pueden los números enamorarse de su propia imagen? decidí dejar para más adelante el hablar de los números conocidos como “errores de impresión”. Ahora, mientras reflexionaba frente a mi ordenador sobre cuál podría ser mi siguiente entrada para el Cuaderno de Cultura Científica, me he acordado de esta familia tan singular de números y me ha parecido que era un buen momento, en mitad de esta larga cuarentena por el coronavirus, para hablar de ellos.
 Doble página del libro Amusements in Mathematics (1917) del matemático recreativo inglés Henry Dudeney
Doble página del libro Amusements in Mathematics (1917) del matemático recreativo inglés Henry Dudeney
El origen de este tipo de números está en un rompecabezas del gran matemático recreativo inglés Henry E. Dudeney (1857-1930), perteneciente al libro Amusements in Mathematics (1917), que dice lo siguiente.
Problema 115, El error de impresión: Para cierto artículo un impresor tenía que escribir 5423, es decir, la multiplicación de la potencia cuarta de 5 (625) por el cubo de 2 (8), cuyo resultado es 5000. Sin embargo, el impresor cometió un error y escribió la expresión 5423, en lugar de la deseada 54 23, lo cual no era correcto. ¿Podrías buscar un número de cuatro dígitos para el cual el error del impresor no hubiese tenido importancia, es decir, las dos expresiones tendrían el mismo valor?
La solución, que es única, a este problema de ingenio es el número 2592, puesto que
![]()
Sin embargo, en el libro de Henry Dudeney no encontramos ninguna explicación, tan solo la respuesta al rompecabezas. Este problema fue propuesto de nuevo unos años más tarde, en 1933, por el matemático norteamericano Raphael M. Robinson (1911-1995), como problema E69, en la revista American Mathematical Monthly. La solución, con su correspondiente demostración (es un análisis de los posibles valores de a, b, c y d, en la expresión abcd= abcd, eliminando todos menos la solución conocida), fue publicada un año después en la misma revista por el matemático Charles W. Trigg (1898-1989).
El aficionado a la matemática recreativa, Donald L. Vanderpool (1930-2010), de Towanda (Pensilvania), no solo se interesó por este problema, sino por encontrar otros ejemplos que también fuesen “errores de impresión”. Del mismo estilo al planteado por Henry Dudeney, aunque el segundo número no era una potencia sino un número natural, encontró los siguientes ejemplos que mostramos a continuación.
Si se les añaden ceros a los números 425 y 325, se obtiene toda una familia infinita de ejemplos, aunque podemos considerar que son esencialmente el mismo.
Donald Vanderpool también obtuvo ejemplos de “errores de impresión” de otro tipo, en concreto, relacionados con las llamadas fracciones mixtas. Primero recordemos qué son estas. Una fracción mixta es una fracción impropia, es decir, el numerador es mayor que el denominador (ambos positivos), luego su valor es mayor que 1, que se representa como un número entero y una fracción propia. Por ejemplo, 3/2 es una fracción impropia, que se representa como 3/2 = 1 1/2, queriendo indicar que es la suma de 1 y 1/2 (esto es, 3/2 = 1 + 1/2, pero en la representación de la fracción mixta se omite el +). Este tipo de representaciones, las fracciones mixtas, se suele utilizar con las medidas (peso, volumen, tiempo, etc), por ejemplo, en las recetas de cocina. Así podemos leer expresiones del tipo “1 1/2 cucharaditas de comino” o “1 3/4 kilogramos de carne picada de ternera” en cualquier libro de recetas de cocina que tengamos en casa, por mencionar alguno, el clásico 1080 recetas de cocina, de Simone Ortega.
Los ejemplos de fracciones mixtas errores de impresión que obtuvo Vanderpool fueron los siguientes.
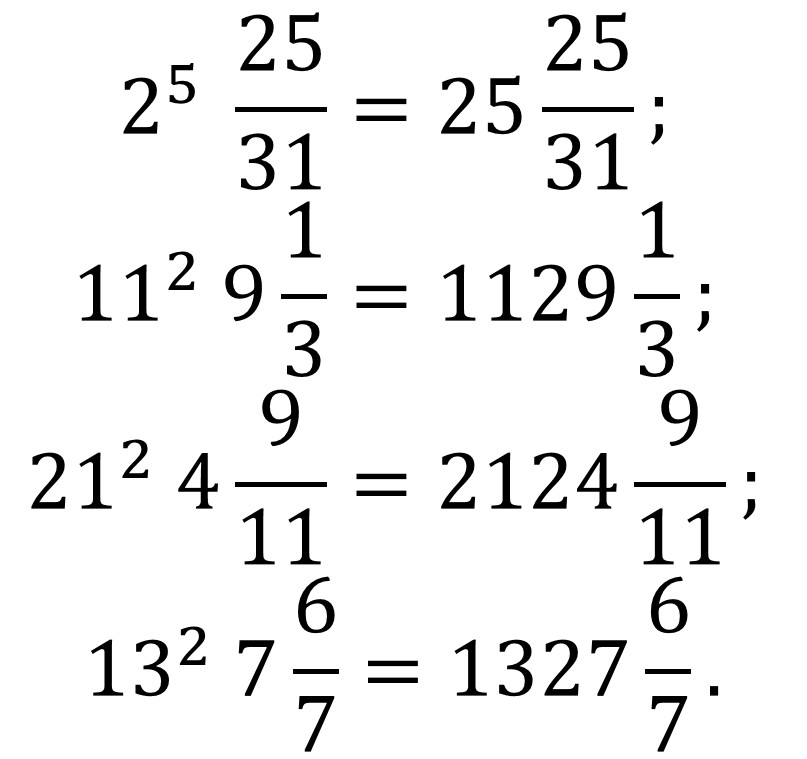 Ejemplos de fracciones mixtas errores de impresión encontrados por el aficionado a la matemática recreativa estadounidense Donald Vanderpool
Ejemplos de fracciones mixtas errores de impresión encontrados por el aficionado a la matemática recreativa estadounidense Donald Vanderpool
Estas fracciones son errores de impresión por lo siguiente.
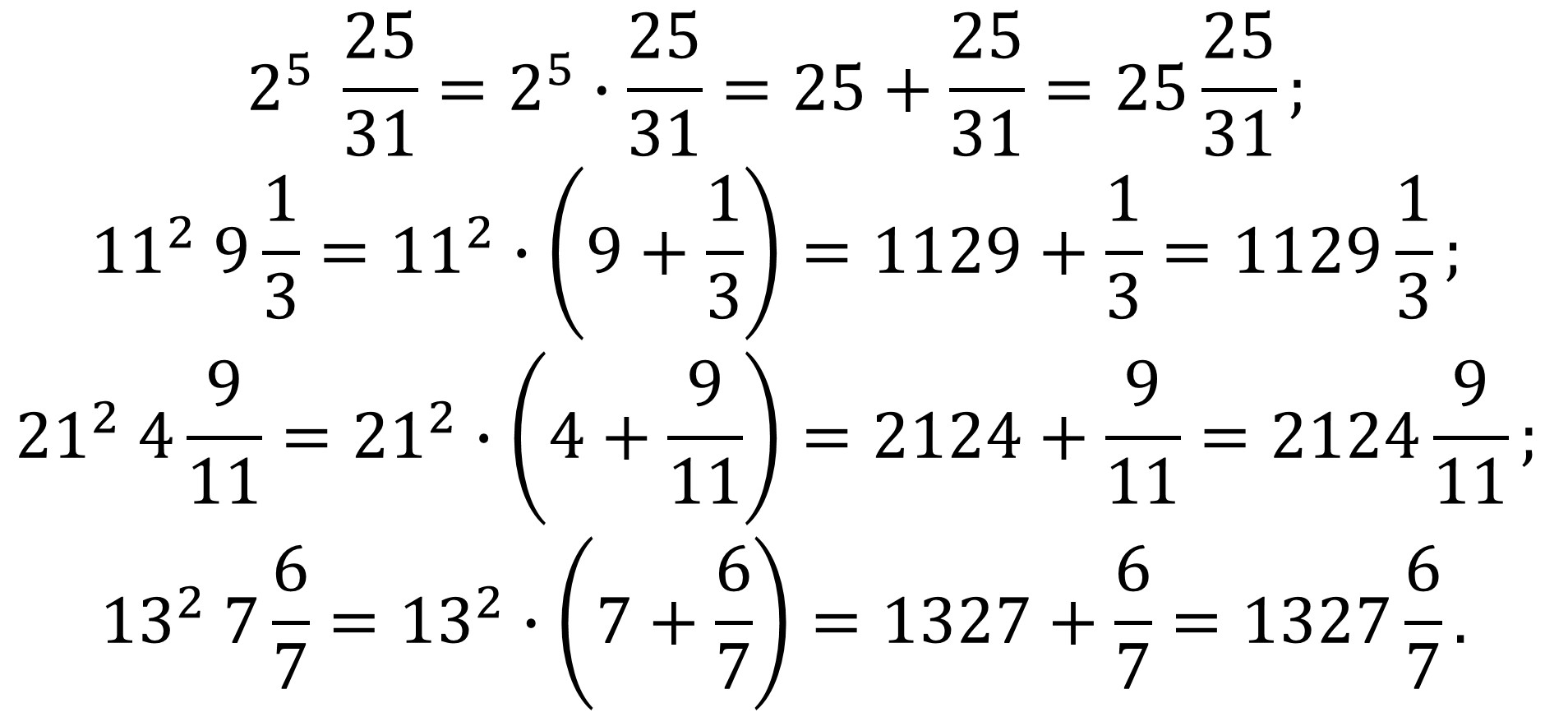
Pero volviendo a los números errores de impresión de tipo Dudeney, es decir, aquellos que son producto de diferentes potencias, es decir, de la forma n = ab cd ef… = abcdef…, aunque tales que, como en los ejemplos de Vanderpool, pueden terminar en un número natural, estos se recogen en la Enciclopedia on-line de sucesiones de números enteros-OEIS como la sucesión A096298. Ahí podemos ver otros números errores de impresión de este tipo.

Si además estas expresiones también pueden empezar por el producto por un número, los llamados números errores de imprenta de segundo tipo (A116890 en la OEIS), tenemos más ejemplos. Algunos de ellos los mostramos aquí.
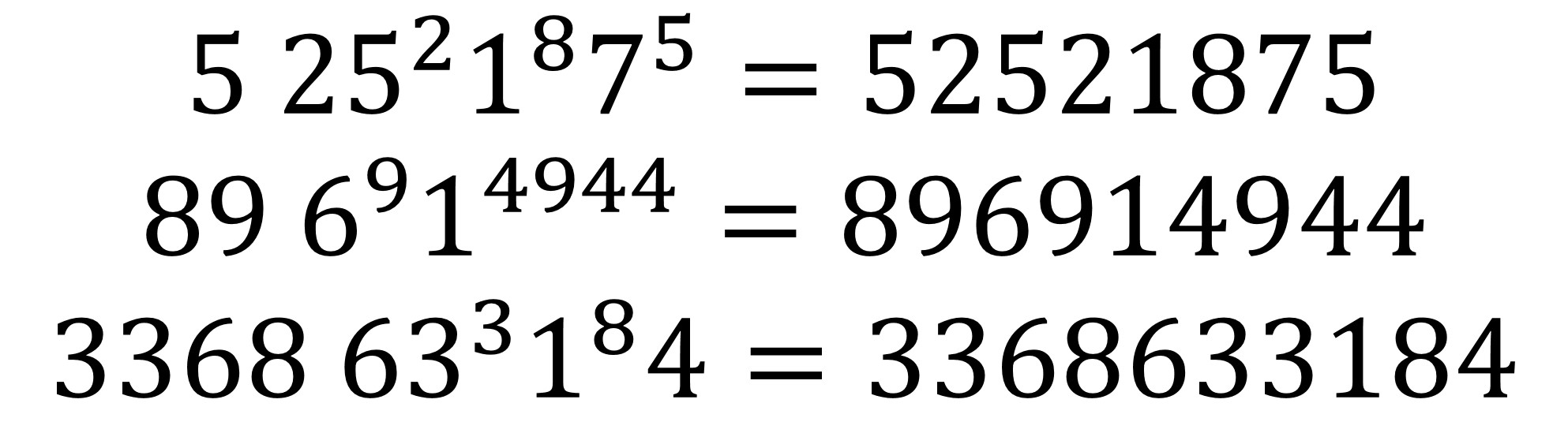
O si admitimos tanto potencias como multiplicaciones (espacios en blanco en la expresión matemática) tenemos más errores de imprenta (A156322 en la OEIS), como los siguientes.
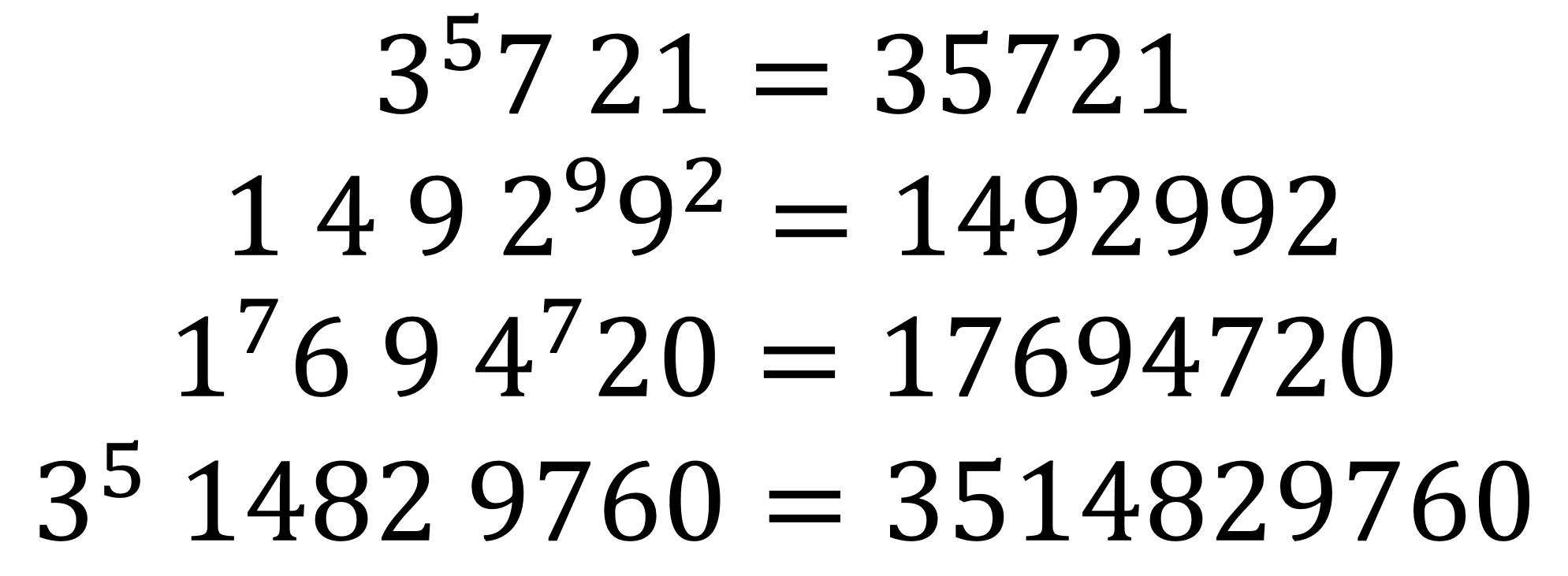
Observemos que el último ejemplo mostrado es pandigital, es decir, tiene las diez cifras básicas, del 0 al 9.
El químico y matemático recreativo estadounidense Joseph S. Madachy (1927-2014) cuando habla de los errores de impresión en su libro Mathematics on vacation, incluye el que caso en que pueda no haber potencias, solo espacios entre números que se entienden como multiplicaciones. El ejemplo que incluye Madachy para explicar esta posibilidad es el siguiente.
![]()
Pero volviendo al problema original, al rompecabezas de Henry E. Dudeney, podemos plantearnos si existirá un ejemplo de error de impresión que sea similar al de Dudeney en el siguiente sentido, que sea producto de potencias con un único dígito en la base y en el exponente, es decir, de la forma abcdef…yz = abcdef…yz. El matemático británico-estadounidense Neil J. A. Sloane, creador de la Enciclopedia on-line de sucesiones de números enteros, demostró que existe sólo otro número como el de Dudeney, al menos para números menores que 10100, teniendo en cuenta que matemáticamente 00 = 1:
![]()
Y como en otras ocasiones vamos a concluir esta entrada del Cuaderno de Cultura Científica con una obra plástica relacionada con los números, en concreto, con el número error de impresión de Dudeney, el número 2592, aunque su autor no se haya inspirado en esta propiedad.
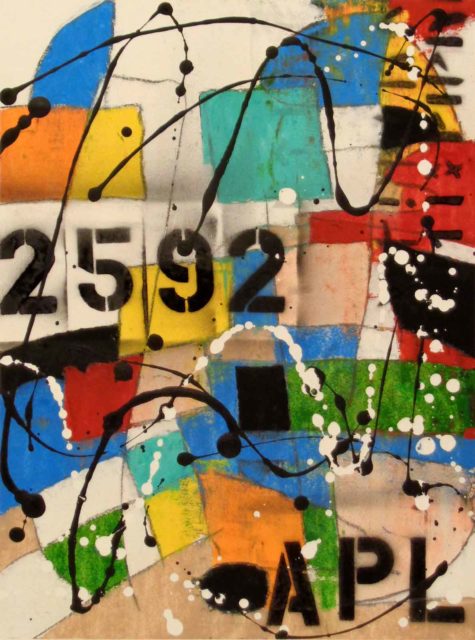 Pintura No. 2592 (2016), del artista estadounidense Al Lofsness
Pintura No. 2592 (2016), del artista estadounidense Al Lofsness
Bibliografía
1.- Henry Dudeney, Amusements in Mathematics, Thomas Nelson and sons,1917 (el original puede verse en la librería Internet Archive).
2.- Donald L. Vanderpool, Printer’s errors, Recreational Mathematics Magazine 10, p. 38, 1962.
3.- Joseph S. Madachy, Mathematics on vacation, Charles Scribner’s Sons, 1966.
4.- Wolfram MathWorld: Printers Errors
5.- Wolfram MathWorld: Mixed Fraction
6.- The On-line Encyclopedia of Integer Sequences
7.- Erich Friedman web page: Math Magic, Problem of the month (June 2001)
8.- Neil J. A. Sloane, Eight Hateful Sequences, Barrycades and Septoku: Papers in Honor of Martin Gardner and Tom Rodgers, American Mathematical Society, 2020.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo Números errores de impresión se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El secreto de los números que no querían ser simétricos
- Números primos gemelos, parientes y sexis (2)
- Buscando lagunas de números no primos
El modelo clásico de electrones libres de Drude-Lorentz
 Foto: Dylan Nolte / Unsplash
Foto: Dylan Nolte / UnsplashDecíamos que nuestros modelos de sólidos cuánticos, si son válidos, deberían poder explicar la ley de Ohm y los distintos tipos de comportamiento conductor que acabamos de describir. Pero para ponerlos en contexto adecuadamente nos será útil un concepto clásico (no cuántico) nuevo, el de gas de electrones.
Poco después del descubrimiento experimental [1] del electrón por parte de Thomson, Paul Drude en 1900 y Hendrik A. Lorentz en 1909 desarrollaron el primer modelo electrónico de la conductividad en un material [2]. En este modelo se supone que el material sólido consiste en átomos metálicos dispuestos en una estructura cristalina que es capaz de vibrar, pero son los electrones el elemento crucial para comprender la conductividad. Los metales conductores como el cobre y la plata tienen un electrón de valencia que se puede separar fácilmente. Drude y Lorentz lo que hacen es suponer que son estos electrones de valencia los que proporcionan la corriente de conducción cuando se aplica un voltaje.
Su modelo se llama habitualmente modelo clásico de electrones libres, clásico porque involucra solo física clásica (no la teoría cuántica) y de electrones libres porque los electrones se consideran pequeñas bolas de materia cargada que son completamente libres para moverse por el material [3]. Solo existe una «fuerza limitante» que actúa sobre los electrones en la superficie de material conductor, evitando que escapen al exterior [4].
En muchos aspectos, los electrones en el modelo Drude – Lorentz de electrones libres forman un tipo de gas ideal, un «gas de electrones» dentro del material conductor. A pesar de la presencia de los átomos de la red, se supone que los electrones se mueven aleatoriamente, como las moléculas en la teoría cinética de los gases, hasta que se aplica un campo eléctrico.
 Fuente: Wikimedia Commons
Fuente: Wikimedia CommonsDado que los electrones están cargados cuando se aplica el campo externo comienzan a moverse en la dirección de la fuerza eléctrica que se ejerce sobre ellos, pero a medida que se mueven experimentan colisiones inelásticas con la estructura cristalina que está vibrando, además de colisiones con las impurezas que pueda haber en el material y con las imperfecciones de la propia estructura cristalina. El resultado es que todas estas colisiones frenan el avance de los electrones y reducen su energía cinética. Esta desaceleración podemos considerarla como un tipo de fricción, y la cantidad de «fricción» podemos llamarla resistencia. La energía cinética perdida aparece como calor. Cuantas más colisiones inelásticas experimentan los electrones cuando atraviesan el conductor, más resistencia encuentran: macroscópicamente esto se expresa como la ley de Ohm.
Por supuesto, si el material está formado por átomos que no tienen electrones de valencia (que se puedan compartir), como vidrio, madera o plástico, no puede haber conducción de electrones y, por lo tanto, no hay corriente cuando se aplica un voltaje. El material es entonces un aislante.
El modelo de electrones libres de Drude-Lorentz explica bastante bien la ley de Ohm, pero no puede explicar algunas de las propiedades térmicas de los metales, además del calor específico, como la dependencia de la resistencia con la temperatura. Además, si los átomos y los electrones obedecen las leyes de la mecánica cuántica, era obvio que se requiere una comprensión mecano-cuántica de la conductividad.
Notas:
[1] Teóricamente se venía hablando de la existencia de los electrones desde hacía décadas. De hecho nos podemos remontar a las especulaciones de Richard Laming sobre la estructura de la materia en la serie de artículos que publicó entre 1838 y 1851. En sentido estricto lo que Thomson demuestra experimentalmente es la existencia de electrones libres (separados de los átomos).
[2] Se sobreentiende que hablamos de un material conductor.
[3] El modelo incluye asunciones más radicales, como que los electrones no están sujetos a fuerzas repulsivas de otros electrones ni a atracciones hacia los iones metálicos.
[4] En el modelo el “exterior” es el “espacio”, en el sentido de que tampoco hay interacciones que influyan.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo El modelo clásico de electrones libres de Drude-Lorentz se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La ley del gas ideal a partir del modelo cinético
- Más allá del modelo de Bohr
- Un modelo simple de gas
Dilemas éticos en la frontera de la ciencia
 Imagen: U.S. National Cancer Institute / Unsplash
Imagen: U.S. National Cancer Institute / UnsplashLos avances científicos y tecnológicos suscitan a menudo la duda de si, además de los beneficios que se puedan derivar de ellos, pueden también dar lugar a perjuicios o, incluso, causar daños que puedan eventualmente llegar a tener efectos catastróficos. El desarrollo científico actual no se ve libre de esos dilemas, que afectan a campos y líneas de investigación en las que se han creado tecnologías con un potencial impresionante. Para ilustrar estos dilemas hemos optado por presentar brevemente aquí tres de esas áreas en las que los avances en la frontera del conocimiento generan debate, inquietud o, incluso, provocan directamente ya la oposición de ciertos sectores sociales. Nos referiremos a la ingeniería genética, la selección de embriones con características prefijadas, y la nanociencia y nanotecnología.
En materia de ingeniería genética, hay asuntos que son objeto de controversia, algunos de los cuales se exponen brevemente a continuación (Spier, 2012).
La posibilidad de secuenciar de forma barata y rápida el genoma de numerosos individuos abre la puerta a que se pida a la gente, implícita o explícitamente, que proporcione su información genética a empleadores o aseguradoras, por ejemplo. Los gobiernos, a través de los sistemas públicos de salud también tendrían acceso a esa información. La intimidad de las personas afectadas se vería en todos esos casos y otros no contemplados aquí claramente vulnerada.
La sustitución o modificación de genes que puedan condicionar la predisposición a ciertas enfermedades, la propensión a determinados rasgos de carácter, el envejecimiento, las habilidades cognitivas, los rasgos físicos, el estado de ánimo, el vigor sexual u otras características también es motivo de preocupación. ¿Dónde se establecerían los límites? ¿Quién los establecería? ¿No supondría la aplicación de estas técnicas una forma de eugenesia “positiva”? En muchos casos se trata de posibilidades todavía lejanas, por las limitaciones técnicas, pero en el supuesto de que bastantes de esas limitaciones se superasen, subsistiría el dilema de si es lícito realizar dichas prácticas o, hasta dónde llegar con ellas (Neri, 2012).
Ya se producen de forma rutinaria animales de laboratorio con características especiales. También organismos a los que se les han inactivado ciertos genes (los ratones knockout son un excelente ejemplo). La biotecnología ha abierto también la puerta a la creación de quimeras o de nuevos organismos con características predeterminadas.
De un orden completamente diferente, pues no conciernen a la naturaleza humana, son las controversias relativas a la producción de organismos transgénicos con propósitos comerciales. Nos referimos, principalmente, a la producción de semillas transgénicas o de animales de esa misma condición, como salmones de crecimiento rápido, por ejemplo. Aunque la mayoría de la comunidad científica coincide en que no se han encontrado pruebas de la peligrosidad de estos organismos, a ellos se oponen sectores sociales y políticos con gran presencia mediática. Esgrimen argumentos de carácter ecológico y razones de salud, pues sostienen que pueden causar un daño grave e irreversible a ecosistemas y seres humanos.
La edición genómica con similares propósitos haciendo uso de las técnicas CRISPR suscita la misma oposición. Es más, el pasado año el Tribunal de Justicia de la Unión Europea sentenció que los organismos que se obtengan mediante la modificación del genoma haciendo uso de esas técnicas han de ser considerados legalmente organismos transgénicos, por lo que les será de aplicación la directiva 2001/18EC. La citada resolución da la razón a varias organizaciones de empresarios agrícolas y grupos ecologistas franceses. La resolución del Tribunal es de gran trascendencia. Dadas las dificultades que han de superarse en la UE para que sea autorizado el cultivo de un transgénico, los obstáculos que deberán salvar los organismos creados mediante edición genética serán similares.
La sentencia no debería extrañar si miramos la forma en que está redactada la normativa europea en materia de organismos modificados genéticamente (OMG). Sin embargo, la decisión no se sostiene desde el punto de vista científico, tal y como explica el genetista y especialista en el uso de estas técnicas Lluís Montoliu.
Volviendo a los seres humanos, con las técnicas hoy disponibles y las que puedan desarrollarse en el futuro inmediato se han abierto posibilidades antes nunca vistas. Para empezar, se pueden hacer diagnósticos genéticos previos a la implantación de embriones, lo que abre la puerta, de entrada, a una eugenesia positiva comentada antes. En noviembre pasado, el científico chino He Jiankui anunció haber creado bebes cuyo genoma había sido editado para hacerlos resistentes al VIH y otros patógenos. El problema, como muchos científicos se encargaron de alertar, es que no es en absoluto descartable que se produzcan errores, que pueden ser fatales o causar daños inasumibles. La clonación plantea problemas similares. Además, hay una gran incertidumbre con los resultados de los tests genéticos, y ser difícilmente interpretables por los interesados (Häyry, 2012).
Por otro lado, las técnicas de reproducción asistida generan también importantes dilemas como el estatus y derechos de un embrión humano viable congelado en caso de muerte de sus progenitores, el recurso a mujeres a quienes se paga para llevar a término un embarazo, la edad de una madre en el momento de la implantación de un embrión, o el desarrollo de clones humanos, entre otros. (Spier, 2012)
De una naturaleza completamente diferente son los dilemas que plantea la nanociencia y nanotecnología por los posibles riesgos que su uso pudiera provocar. Según Maynard et al (2006) y Johnson (2012), es posible que el temor a los posibles peligros de algunas nanotecnologías sea exagerado, pero no carece necesariamente de fundamento. Investigaciones que han analizado la toxicidad de nanomateriales en cultivos celulares y animales han mostrado que el tamaño, el área superficial, la química de la superficie, la solubilidad y quizás la forma influyen en cierta medida en el daño que puede producir los materiales de dimensiones nanométricas. Y por otro lado, hay quien duda de que la ciencia disponga de la tecnología adecuada para evaluar esos posibles daños.
Entiéndase que los tres casos expuestos lo son a modo de ejemplo de muchos otros posibles (inteligencia artificial, “big data”, uso de robots, etc.)
Fuentes:
Además de las enlazadas en el texto, las fuentes utilizadas han sido los artículos de la Encyclopedia of Applied Ethics referenciados a continuación:
Häyry, M (2012): Genetic Engineering of Human Beings, in Encyclopedia of Applied Ethics, Vol II, pp.: 437-444, 2nd edition, Academic Press, London
Johnson, S (2012): Nanotechnology, in Encyclopedia of Applied Ethics, Vol III, pp.: 183-185, 2nd edition, Academic Press, London
Neri, D (2012): Eugenics, in Encyclopedia of Applied Ethics, Vol 1, pp.: 189-199, 2nd edition, Academic Press, London
Spier, R E (2012): Science and Engineering Ethics, Overview, in Encyclopedia of Applied Ethics, Vol 4, pp.: 14-31, 2nd edition, Academic Press, London
Este artículo se publicó originalmente en el blog de Jakiunde. Artículo original.
Sobre los autores: Juan Ignacio Perez Iglesias es Director de la Cátedra de Cultura Científica de la UPV/EHU y Joaquín Sevilla Moroder es Director de Cultura y Divulgación de la UPNA.
El artículo Dilemas éticos en la frontera de la ciencia se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- «Dilemas éticos en la experimentación animal» por Jesús Mosterín
- No todo vale al servicio de la ciencia
- Ciencia y democracia: dilemas de la divulgación científica
Epigenética, desigualdad y cambio climático
Emilio Muñoz Ruiz y Jesús Rey Rocha
 Arabidopsis thaliana. Fuente: Shutterstock/lehic
Arabidopsis thaliana. Fuente: Shutterstock/lehicUno de nosotros (Emilio Muñoz) estudia desde hace décadas la filosofía de la biología, con la evolución como soporte analítico. Este trabajo ha promovido la importancia de la regulación. Este artículo persigue aumentar la difusión de las relaciones entre el sorprendente fenómeno de regulación biológica con algunos de los grandes retos sociales y riesgos ambientales.
La epigenética ha experimentado avances impresionantes desde que en 1942 Conrad Waddington empezó a proponer este mecanismo bajo una visión híbrida, entre genética y embriología, para conectar el genotipo (el patrimonio genético de cada ser vivo) y el fenotipo (los caracteres perceptibles), incluso antes de conocer de qué estaban hechos los genes. El término hoy día engloba todos los procesos de regulación de la expresión génica, tanto en el desarrollo como en respuesta a las señales externas.
La epigenética en 2020 y más allá
Los mecanismos epigenéticos conocidos son cada día más variados. Esta variedad es mucho mayor en los organismos con núcleo celular (eucariotas) que en los más sencillos procariotas (bacterias y arqueobacterias). Existen datos fehacientes sobre procesos de transmisión a la descendencia: la langosta del desierto (Schistocerca gregaria) cambia su comportamiento en cuanto a agresividad, gregarismo e incluso estrategia de supervivencia, en cuanto se reúnen tres ejemplares de la especie.
 Schistocerca gregaria.
Schistocerca gregaria.Shutterstock/Benny Marty
Todos estos cambios que se conservan en la descendencia,los induce una única molécula, un precursor de la dopamina, la levodopa, que desencadena una serie de alteraciones en el desarrollo que se reflejan en la fisiología, un proceso que podemos considerar epigenético. Para reforzar estos argumentos: el comportamiento gregario induce grandes cambios en la expresión de los genes por el incremento en el nivel de otro neurotransmisor, la serotonina; sin estar codificado en los gametos, las madres los transmiten de generación en generación.
Una pregunta precisa se orienta de modo decisivo a mostrar evidencias que justifiquen la heredabilidad de las modificaciones epigenéticas. Vincent Colot, director de investigación del Centro Nacional para la Investigación Científica de Francia, ha obtenido resultados fascinantes en plantas (Arabidopsis thaliana) que se resumen del modo siguiente: “Individuos que, con el mismo genoma, difieren en su perfil de metilación, una parte de cuyas diferencias se transmiten a lo largo de generaciones”.
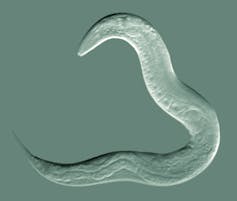 C. elegans.
C. elegans.Bob Goldstein
A la pregunta ¿y en los animales? tanto Colot como Edith Heard, directora del Laboratorio Europeo de Biología Molecular en Heidelberg (Alemania) ofrecen ejemplos del gusano Caenorhabditis elegans. Este reacciona a agresiones ambientales con la producción de ácidos ribonucleicos (ARN) de pequeño tamaño, procesos de respuesta que se refuerzan y mantienen durante generaciones. Lo más sorprendente es que existe un mecanismo de retroacción que decide si perdura o se elimina esta respuesta epigenética.
Por su parte, Heard expone el caso de ratones derivados de experimentos del año 2000, en los que el gen que controla el color del pelaje – vía melanina – podía experimentar procesos de metilación que se conservan durante generaciones de forma estable con variabilidad en la progenie. Asimismo, es muy significativo que el régimen alimenticio parezca jugar un papel en mantener la herencia del estado deseado.
Incursión en la filosofía: evolución y selección natural
¿Qué papel tienen los estados epigenéticos sobre un proceso tan complejo como la selección natural? En línea con la cultura francesa, entramos en el terreno filosófico, donde las respuestas ya no pueden ser tan rotundas.
Los datos que ofrece Colot en Arabidopsis son significativos a nivel experimental con el modelo de plantas y tienen que ver con la intervención de esos elementos celulares fascinantes que son los transposones. Barbara McClintock, una heroína de la biología molecular, los descubrió en el maíz en la década de los 40 del siglo pasado, descubrimiento por el que recibió el Premio Nobel de Fisiología o Medicina en 1983.
 Barbara McClintock.
Barbara McClintock.Smithsonian
Heard, con menos experiencia sobre tales elementos al trabajar con animales, apostilla lo siguiente: “Recuperamos una hipótesis que Barbara McClintock formuló en 1950 cuando los descubrió; los consideraba elementos de control de la expresión de los genes, aunque no hablaba de epigenética”.
Los científicos, aún dentro de la prudencia, hablan del fenómeno de “plasticidad fenotípica”. Según esta, los transposones y sus vestigios podrían tener como función última la adaptabilidad para la selección natural. Heard reconoce este papel de los transposones y se pregunta algo tan valiente como “si son esenciales para la adaptación a entornos diferentes, las plantas quizá sean ejemplos más llamativos porque no se desplazan mientras que los animales gozan de esta propiedad”. Una afirmación plena de inteligencia y lógica científica.
Lamarck, al estrado
Con estos avances en la comprensión del fenómeno epigenético ya no se puede eludir la pregunta de que si hay que revisar los planteamientos de Lamarck. Colot, cultura francesa, admite que “el acercamiento se vuelve interesante”. Heard, educada en Cambridge y más rotunda en la _fe_por Darwin, señala que “el mecanismo que propuso Lamarck para adquirir rasgos hereditarios no es admisible porque la base de la selección son las mutaciones, son el motor último de la evolución”.
No obstante, reconoce que Lamarck tenía razón “al decir que hacían falta respuestas flexibles y rápidas al entorno y esto abriría la posibilidad a la plasticidad fenotípica de ser el motor de cambios más remotos”.
Interdependencia entre evolución, desigualdad y cambio climático
En función de lo que se ha expuesto sobre el potencial de la epigenética, se plantea una visión analítica de la relación entre evolución y dos grandes desafíos ambientales.
Uno es la desigualdad como gran reto social para la democracia neoliberal que ha sido promovida por el neoliberalismo especulativo, como ya sostienen con instrumentos de la ciencia económica un importante grupo de economistas como Stiglitz, Deaton, Piketty, Galbraith, Sachs y Pilling.
Otro es el cambio climático como gran desastre ambiental, tesis que ya incorporan economistas y un importante número de científicos de la ciencia del clima, que cuenta con un acervo impresionante de datos, opiniones y reclamaciones para la acción.
La desigualdad explotada desde el ámbito del desafío social deriva en la generación de riesgos ambientales para individuos, familias y colectivos que la sufren, como la pobreza energética, la dependencia, las preocupaciones económicas o problemas de salud mental. Tales presiones evolutivas relacionadas con la calidad de vida se pueden agravar en una sociedad tan consumista como la actual.
El cambio climático es el enorme riesgo ambiental de nuestros tiempos que causa y potencia los retos sociales: además su influencia con la producción de desastres naturales de notables dinámicas y dimensiones sobre los acervos genéticos y epigenéticos, puede llegar hasta a inducir mutaciones.
No seamos apocalípticos pero si analíticos. Proponemos la siguiente pauta de acción: “Más pensamiento crítico y reflexión, y menos populismo modelo Trump y Bannon”
La versión original de este artículo aparece publicada en la web de la Asociación Española para el Avance de la Ciencia (AEAC). Está inspirado en un artículo de la revista Investigación y Ciencia.![]()
Emilio Muñoz Ruiz es profesor de investigación y Jesús Rey Rocha investigador en el Instituto de Filosofía del Consejo Superior de Investigaciones Científicas (IFS-CSIC), Centro de Ciencias Humanas y Sociales (CCHS – CSIC)
Este artículo fue publicado originalmente en The Conversation. Artículo original
El artículo Epigenética, desigualdad y cambio climático se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Geología, Antropoceno y cambio climático
- Verdín, eucaliptos y cambio climático
- Los ecosistemas acuáticos de África y el cambio climático
Física, ingeniería, geología y ética en (el estudio de) los deslizamientos de ladera
Los fósiles, los minerales o las rocas son, entre otras cosas, en lo primero que pensamos al hablar de geología, pero lo cierto es que la física es un ámbito científico que difícilmente se puede desvincular de la geología. Y es que el fundamento físico resulta clave a la hora de explicar algunos procesos geológicos que suceden tanto en el océano como en la superficie terrestre.
Con el fin de poner sobre la mesa la estrecha relación entre la geología y la física, los días 27 y 28 de noviembre de 2019 se celebró la jornada divulgativa “Geología para poetas, miopes y despistados: La Geología también tiene su Física”. El evento tuvo lugar en la Sala Baroja del Bizkaia Aretoa de la UPV/EHU en Bilbao.
La segunda edición de esta iniciativa estuvo organizada por miembros del grupo de investigación de Procesos Hidro-Ambientales (HGI) de la Facultad de Ciencia y Tecnología de la Universidad del País Vasco, en colaboración con el Vicerrectorado del Campus de Bizkaia, el Geoparque de la Costa Vasca y la Cátedra de Cultura Científica de la UPV/EHU.

La observación de la naturaleza (geología) permite crear modelos (física) sobre los que establecer posibilidades de actuación (ingeniería) con unos condicionantes sociales (ética) en algo con tanto impacto para las poblaciones humanas como los deslizamientos de ladera. La reflexión corre a cargo de Antonio Casas, profesor del departamento de ciencias de la Tierra de la Universidad de Zaragoza.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Física, ingeniería, geología y ética en (el estudio de) los deslizamientos de ladera se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Geología, ver más allá de lo que pisamos
- Otra mirada al planeta: arte y geología
- ¡Leamos poesía astronómica en las rocas!
Guetos animales
 Foto: Bruno Glätsch
Foto: Bruno GlätschUn equipo de investigación internacional en el que participan expertos de la UPV/EHU ha demostrado que las especies raras –entendidas estas como poco abundantes- se asocian espacialmente en el 90% de las comunidades de animales y plantas estudiadas.
“Las comunidades de animales y plantas se organizan igual que lo hacemos en las ciudades, en guetos o barrios étnicos”, determinan los investigadores. Esta organización podría estar detrás de la persistencia de especies raras, ya que estas podrían evitar la presión competitiva de las especies más abundantes, bien porque cooperan entre ellas o porque prefieren microhábitat concretos “o ambas cosas a la vez”.
Los resultados de esta investigación sugieren una explicación general para el mantenimiento de la biodiversidad en ambientes competitivos, matizando el principio de exclusión competitiva por el que las especies con las habilidades competitivas más bajas deberían ser excluidas por las competidoras más eficientes.
“Este patrón podría explicar cómo especies que compiten por los mismos recursos son capaces de coexistir”, comentan los biólogos.
Para llevar a cabo el estudio, se han analizado más de trescientas comunidades ecológicas de musgos, hierbas, árboles, insectos, arácnidos y corales, entre otros, distribuidas por todo el mundo.
Los investigadores explican que, para detectar los guetos o grupos, utilizaron la teoría de redes mientras que para estudiar los mecanismos que daban lugar a ellos aplicaron simulaciones numéricas. Los resultados de estas simulaciones constatan que la agrupación entre especies poco abundantes es necesaria para explicar los patrones de coexistencia observados a escala mundial.
Estos hallazgos pueden tener profundas implicaciones para la comprensión de la formación de las comunidades ecológicas. Entre sus aplicaciones, los expertos destacan la planificación de la conservación o incluso el estudio de enfermedades humanas relacionadas con el microbioma intestinal, “donde la coexistencia de especies es fundamental”.
“Sin embargo, aún se desconocen las interacciones y mecanismos específicos que permiten asociaciones de especies raras, lo que también debería impulsar una nueva agenda de investigación en varios campos de las ciencias de la vida”, reconocen.
Referencia:
Calatayud J. et al. (2019) Positive associations among rare species and their persistence in ecological assemblages Nature Ecology & Evolution doi: 10.1038/s41559-019-1053-5
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Guetos animales se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Animales eurihalinos
- Un nuevo mecanismo de resistencia antifúngico
- ¿Cuántos animales se usan en España para experimentación?
Ingredientes para la receta: Los cítricos
Cidra: Fruto del cidro, semejante al limón, y comúnmente mayor, de sabor agrio, cuya corteza gorda y carnosa está sembrada de vejiguillas muy espesas, llenas de aceite volátil, que se usa en medicina.
 Foto: Ben Ashby / Unsplash
Foto: Ben Ashby / UnsplashLos cítricos son especies, varias de ellas comestibles, que pertenecen al género Citrus, de la familia Rutaceae, y tienen su origen en Asia. Llegaron a Europa por las rutas comerciales y de conquista con Asia oriental hace unos 3500-5000 años. En la actualidad y según la FAO, con cifras de 2016, la mayor producción de cítricos es la de China, seguida de la cuenca mediterránea, con España como primer productor, y en tercer lugar aparecen Brasil y Estados Unidos.
La taxonomía de las especies comestibles del género Citrus es complicada. David John Mabberley, de la Universidad de Leiden, en Holanda, escribía hace unos años que, según los debates entre los expertos, el número de especies comestibles varía de 1 a 162. Mabberley afirma que, en general los autores siguen la clasificación de Swingle, publicada en 1944, con 12 especies comestibles. El propio Mabberley concluye que son 3 especies y 4 grupos de híbridos, con decenas de variedades. La facilidad de producir híbridos entre las especies y de estas con híbridos ya existentes hace que el número de variedades crezca sin cesar y complica la clasificación que está, además, siempre en continua revisión.
 Cidra (Citrus medica). Imagen: Wikimedia Commons
Cidra (Citrus medica). Imagen: Wikimedia CommonsPara Mabberley y Dafna Langgut, de la Universidad de Tel Aviv, las especies originales son, en primer lugar, la cidra, Citrus medica, del Himalaya y el sur de China, que, a su vez, participa en dos grupos de híbridos: el limón, híbrido de la cidra con Citrus limon, y está en debate su relación con la lima; y el híbrido con Citrus jambhiori o limón arrugado.
La segunda especie es el pomelo chino, Citrus maxima, de Malasia, con dos híbridos: para la lima hibrida con el Citrus aurantiifolia; y para naranjas amarga y dulce con Citrus aurantium.
La tercera especie, según Mabberley, es la mandarina o Citrus reticulata, que viene del sur de China y del norte de Myanmar. Sus muchos híbridos también se conocen como mandarinas.
La revisión de la taxonomía de los cítricos que publicó Mabberley años después, en 2004, es la mejor herramienta para conocer la complicada taxonomía del género Citrus y de los híbridos de sus especies.
Las zonas de origen de los cítricos coinciden con las que propuso Vavilov como origen de especies cultivadas en Asia, con el sur de China, los Himalayas e Indochina. Sin embargo, solo conocemos en detalle las especies que llegaron a Europa como comestibles y se clasificaron según Linneo. Queda mucho por conocer para integrar los cítricos asiáticos en un esquema general junto a las especies comestibles conocidas en Europa.
Los cítricos llegaron a Europa después de su cultivo en Asia durante milenios. En China se les menciona en textos que se cree se redactaron hace más de 4000 años, o en escritos de los tiempos de la dinastía Chou de hace 3000 años.
Después, los cítricos llegaron a Birmania y a la India. En este país, ya se cultivaban otras especies de cítricos y, por ello, la terminología en textos antiguos es confusa. Limones y limas han aparecido en las excavaciones de Mehenjo-daro, en el valle del Indo, en el actual Pakistán, y con fecha de hace unos 4000 años.
El estudio del ADN de los cítricos, publicado en 2018, confirma que su origen está a los pies del Himalaya, en la zona de Assam, en la India, en Yunnan en China, y al norte de Birmania, en la actual Myanmar.
Ahora, la naranja es naranja en España y Hungría. En Alemania es orange, applelsine o pomeranze. Pomeranz es en Polonia y apielcine en Rusia. También es arancia en Italia, y orange en Francia y en Inglaterra. Y laranja en euskera. Todo tiene su origen en aquel na ranga del sánscrito en la India o, quizá, como naranga, puede venir del tamil.
 Foto: Hans Braxmeier / Pixabay
Foto: Hans Braxmeier / PixabayLas semillas más antiguas de cidra encontradas en Europa proceden de las excavaciones de Hal Sultan Tekke, en Chipre. Fueron dos semillas y están fechadas hace 3200 años. También se han identificado granos de polen de cidra en el yacimiento de Ramat Rahel, cerca de Jerusalén, y vienen, quizá, de algún árbol del jardín de un personaje importante. Con una fecha parecida, ha aparecido un grano de polen de cidra en las excavaciones de Cartago, en el actual Túnez.
El primer cítrico cuyo cultivo se extendió por Europa fue la cidra. Su historia es complicada. Hay algunos términos en sánscrito que parece se refieren a esta fruta pero, también, se ha propuesto que su origen está en Arabia. La variedad árabe llegó a Mesopotamia y Persia, done la encontraron los griegos con las conquistas de Alejandro Magno en el Próximo Oriente. Han aparecido semillas de cidra en las excavaciones de Nippur, en Mesopotamia y, ahora, en Irak, fechadas hace unos 6000 años.
El griego Teofrasto fue el primer autor clásico que describió la cidra en su Historia de las plantas, que se supone se escribió hacia el año 310 antes de nuestra era:
En el este y sur hay plantas especiales… es decir, en Media y Persia hay muchos tipos de frutas, entre ellas hay una fruta llamada manzana persa o media. El árbol tiene una hoja similar y casi idéntica a la del audrácnico, pero tiene espinas como las de los apios. O la espina de fuego, excepto que son blancos, lisos, afilados y fuertes. El fruto no se come, pero es muy fragante, como también lo es la hoja del árbol; y la fruta se pone entre las ropas, evita que las coman las polillas. También es útil cuando uno ha bebido veneno mortal, para cuando se administra en vino; altera el estómago y saca el veneno. También es útil para mejorar la respiración, ya que si uno hierve la parte interna de la fruta en un plato o la exprime en la boca en algún otro medio, hace que la respiración sea más agradable. La semilla se retira de la fruta y se siembra en primavera en camas cuidadosamente labradas, y se riega cada cuarto o quinto día. Tan pronto como la planta es fuerte, se trasplanta, también en primavera, a un sitio suave y bien regado, donde el suelo no es muy fino, ya que prefiere esos lugares.
Y da sus frutos en todas las estaciones, porque cuando algunos se han reunido, la flor de los demás está en el árbol y está madurando a otros. De las flores que he dicho, las que tienen una especie de rueca que se proyectan desde el centro son fértiles, mientras que las que no tienen esta son estériles. También se siembra, como las palmeras, en macetas perforadas con agujeros.
Hace 2000 años, naranjas amargas y limones ya habían llegado a Europa y en la Roma imperial, como ejemplo, nos sirve su presencia en frescos y mosaicos de Pompeya o en diferentes lugares del Mediterráneo como Egipto, Palestina o Nápoles. Se supone que, más que como alimento, eran árboles de adorno en jardines públicos y en las mansiones de gente pudiente. También citan la cidra en sus escritos, autores clásicos romanos como Virgilio o Plinio el Viejo.
Sin embargo, Marco Gavio Apicio, que vivió en el siglo I y fue el más reputado gastrónomo romano, citó en varias ocasiones a la cidra en su libro De re coquinaria. Aconseja, para conservar las cidras en su despensa, que se pongan “en un recipiente, cubrirlas con yeso y colgarlo”. Con esta fruta, Apicio elaboraba vino de rosas sin rosas: “Poner hojas de cidro verdes en un pequeño capazo de palma dentro de una jarra de mosto sin fermentar y, después de cuarenta días, las sacas. Si fuera necesario, añades miel y lo sirves en sustitución del vino de rosas”.
Algo más contundente es su receta de “picado dulce de cidras”:
Pones en la olla aceite, garum, caldo, puerro entero, cortas cilantro bien pequeño, un lomo de cerdo cocido y albóndigas pequeñas. Mientras cuece, mueles pimienta, comino, cilantro verde o semilla, ruda verde y raíz de laserpicio. Viertes vinagre, vino cocido, caldo del que haga el guiso, lo ligas con vinagre y lo hierves. Cuando haya hervido, pones la cidra en la olla, bien limpia por dentro y por fuera, hervida y cortada en trocitos pequeños. Pones pasta desmenuzada y lo ligas todo. Echar pimienta y lo presentas.
Los romanos también conocían el limón y, en excavaciones en el Foro Romano fechadas hace 2000 años, se han encontrado 13 semillas y un fragmento de piel. Cerca del Vesubio han aparecido restos de madera de limonero, e imágenes de la fruta en pinturas y mosaicos. De nuevo, como con la cidra, era un árbol para jardines de personajes importantes.
Los judíos cultivaban cidras para su Fiesta del Tabernáculo o Sucot y, en su diáspora, la llevaron por toda la cuenca mediterránea. La variedad que recogían es la llamada etrog, siempre pura o no híbrida ni injertada.
Los árabes extendieron por el norte de África y el sur de Europa, en el siglo X, limones, lima, pomelos y naranjas amargas. Una receta árabe del siglo XIII, de Muhammad el-Khatib, de Bagdad, nos la cuenta Helena Attlee en su gran y muy recomendable libro sobre la historia de los cítricos en Italia:
Hervir a fuego lento cordero en tacos, puerro, cebolla y zanahoria picados. Añadir comino, semillas de cilantro, canela, jengibre, pimienta, lentisco molido y unas hojas de menta. Cuando esté casi hecho, hacer albóndigas con todo. En una cazuela poner menta seca y zumo de naranja amarga. Añadir semillas molidas de cardamomo y las albóndigas y cocer a fuego suave. Servir con menta seca espolvoreada.
En el siglo XIII existía en la cocina de Florencia una receta de pato a la naranja, con pato salvaje y naranja amarga. Y en el Llibre de Sent Sovi, recetario de cocina valenciana y catalana medieval, publicado en 1324, ya se citan cidras, naranjas y limones.
Otra historia curiosa relacionada con las naranjas acaeció en Navarra en el siglo XV. Era el año 1421 cuando Leonor de Castilla, esposa de Carlos III de Navarra, después de comer una bigarda, una variedad de naranja de sabor fuerte y amargo, le gustó tanto que plantó cinco semillas en un tiesto. Y prendieron y crecieron en Pamplona hasta 1499 cuando Catalina, esposa de Juan III, rey de Navarra, regaló los cinco naranjos a Ana de Bretaña, casada con Luis XII de Francia, y, además, le relató su historia. Se dice que fueron los primerso naranjos en llegar a Francia donde, con los años, fueron muriendo, y el último lo hizo en Versalles en 1858 o en 1894, según opiniones de diferentes expertos, casi cinco siglos después de su plantación.
Fueron primero los genoveses y, después, los portugueses los que, en los siglos XVI y XVII transportaron la naranja dulce a Europa.
En el siglo XVI, en Italia, los cítricos eran populares y muy utilizados en las grandes casas para sus exquisiteces gastronómicas. Linda Civitello cuenta que, en 1529, el arzobispo de Milán ofreció una cena con 16 platos que incluía
Caviar y naranjas fritas con azúcar y canela, sardinas con rodajas de naranja y limón, ostras con pimienta y naranjas, ensalada de langostas con cidras, esturión con gelatina cubierto con jugo de naranjas, gorriones fritos con naranja, ensaladas personalizadas para cada comensal con cidras y los brazos de los invitados tallados con ellas, buñuelos de naranja, suflé de pasas y piñones cubiertos de azúcar y jugo de naranja, quinientas ostras fritas con rodajas de limón, peladuras de cidra y naranjas confitadas.
Del 1600 en adelante, un testimonio muy visible de la presencia de cítricos en Europa lo dan los bodegones y naturalezas muertas de los pintores holandeses. Allí aparecen, por su color y su forma, muchos cítricos, sobre todo limones y naranjas. Brian Wansink y sus colegas, de la Universidad Cornell de Ithaca, cuentan como los cítricos aparecen en los bodegones holandeses de los siglos XVI y XVII. Los limones son las figuras más importantes y aparecen en el 51% de las obras holandesas analizadas, seguidos de las naranjas en el 14% de los cuadros.
 Orangerie de Versalles en verano (en invierno los naranjos están en el invernadero). Los naranjos están en cajones para poder transportarlos. Fuente: Wikimedia Commons
Orangerie de Versalles en verano (en invierno los naranjos están en el invernadero). Los naranjos están en cajones para poder transportarlos. Fuente: Wikimedia CommonsLuis XIV, gran aficionado a las naranjas, construyó en Versalles un “orangerie”, una especie de enorme invernadero almacén para conseguir una temperatura adecuada para el cultivo de naranjas. Era tan amplio que se utilizaba para bailes, conciertos y para las obras de teatro que tanto gustaban al Rey Sol. En las “orangeries”, el aroma a flor de azahar era tan intenso que así lo describió La Fontaine en unos versos:
Orangers, arbres que j’adore
Vos fleurs ont embaumé tout l’air
Que je respire.
En su Nuevo arte de cocina publicado en 1745, Juan Altamiras, fraile franciscano aragonés, escribe alguna receta con naranjas amargas. Para hacernos con los sabores árabe-bereberes que, además, fueron los que trajeron a la Península la naranja amarga, nos ayuda una receta, Pechuga de pollo en salsa de naranja, que escribe Benavides-Barajas en su Nueva-clásica cocina andalusí:
Se sofríen las pechugas en un poco de aceite y, después, se ponen en la cazuela con zumos de naranja y un poco de limón. Se cuece y reduce y se añade algo de mantequilla, menta picada, cilantro y nueces molidas o avellanas. Espolvorear con pimienta y servir.
Parece ser que fue en 1791 cuando se inició la primera plantación moderna de naranjas dulces como cultivo comercial. Fue en Carcagente y se atribuye a la iniciativa del sacerdote Vicente Monzó. Por su éxito, siguieron otras plantaciones en Burriana y Villarreal, en la provincia de Castellón.
Y ya en el siglo XIX, en 1805, llegó a Europa la mandarina, en 1850 estaba bien establecida en Italia, después de pasar por Malta y Sicilia. A España llegó en 1845 y se empezó a cultivar en Castellón en 1856. Llegó a Europa por el encargo de un mecenas, Sir Abraham Hume, que encargó le trajeran dos plantones desde Catón. Hume se los entregó a Sir Joseph Banks, del Real Jardín Botánico de Kew, que, a su vez, donó semillas a Malta, y para 1821 ya crecía en el Jardín Botánico de Palermo, en Sicilia.
Para resumir lo anterior, podemos utilizar la revisión de Dafna Langgut, publicada en 2017, sobre la llegada de cítricos al Mediterráneo. La cidra apareció hace unos 2500 años con los persas; el limón hace unos 2000 años con los romanos; la naranja amarga, la lima y el pomelo llegaron con los árabes entre los siglos X al XII; la naranja dulce con genoveses y portugueses en los siglos XV y XVI; y la mandarina en el siglo XIX con los británicos.
 Foto: Michele Hayes / Unsplash
Foto: Michele Hayes / UnsplashPara ilustrar los cítricos con una receta actual no hay mejor ejemplo que las Naranjas “asás” de la Cocina para pobres del doctor Alfredo Juderías en su undécima edición de 1994.
Se pelan unas buenas naranjas, procurando que la cortezuela salga entera, y se desgajan un poquejo. Se echa azúcar, así como un par de garbanzos de mantequilla y una chispa de canela. Se ponen en una fuente refractaria, previamente engrasada, y se meten al horno a fuego suave. Se retiran; se dejan enfriar y se sirven adornadas y cordoneadas por su propia envoltura.
Y, no hay que olvidar, están los licores elaborados con cítricos. Por ejemplo, el Cointreau, cuya historia nos cuentan Amilcar Duarte y sus colegas, de la Universidad del Algarve. Es el licor más conocido elaborado con cítricos, en concreto con piel de naranjas dulce y amarga macerada en alcohol y destilado tres veces para concentrar los aromas. Lo inventaron los hermanos Adolphe y Edouard-Jean Cointreau y, desde 1849, lo elaboran en Angers.
Algo parecido tenemos aquí cerca, el Licor Karpy que elaboran las Destilerías Acha, de Amurrio, desde 1930. Maceran peladuras de naranjas dulces y amargas por separado. Después de la maceración, mezclan glucosa, fructosa, alcohol y agua destilada. Dejan reposar de dos a tres meses, lo filtran y embotellan. Por cierto, las naranjas, una vez peladas, se vendían a los vecinos de Amurrio y a la fábrica de refrescos KAS.
Todas estas bebidas con alcohol, algún cítrico macerado y azúcar nos cuentan la historia del escorbuto y de la Armada Real inglesa. La enfermedad era un azote para los marineros en sus largas travesías y, a menudo, llegaba a matar a la mitad de la tripulación. Hasta no hace mucho se desconocía que el escorbuto era provocado por la falta de vitaminas, sobre todo de vitamina C, y de minerales pues no se consumían, en aquellos largos viajes, frutas y verduras frescas. Fue James Lind, médico de los barcos de la Armada Real, el que organizó un experimento con zumo de cidra durante una travesía por el Golfo de Vizcaya. En 1753 publicó su libro Tratado sobre el escorbuto, en el que explicaba como los marineros, con una ración diaria de zumo de cidra, evitaban el escorbuto. Años después, en 1795, el Almirantazgo decidió incluir zumo de lima o de limón en las provisiones de los barcos. Y fue Edward Vernon, un oficial de la Armada, el que decidió unir el zumo de lima con la ración diaria de ron de cada marinero. Desapareció el escorbuto de la Armada Real, excepto en casos muy concretos.
Referencias:
Alvarez, B.T. 2015. La cidra, el primer cítrico conocido en Europa. UAM Gazette. Unidad de Cultura Científica. Universidad Autónoma de Madrid. 16 julio.
Apicio, M.G. 2007. El arte de la cocina. De re coquinaria. Comunicación y Publicaciones SA. Barcelona. 119 pp.
Attlee, H. 2017. El país donde florece el limonero. La historia de Italia y sus cítricos. Acantilado. Barcelona. 316 pp.
Baron, J.H. 2009. Sailors’ scuvy before and after James Lind – a reassessment. Nutrition Reviews 67: 315-332.
Benavides-Barajas, L. 1995. Nueva-clásica cocina andalusí. Ed. Dulcinea. Granada. 328 pp.
Brothwell, D. & P. Brothwell. 1969. Food in Antiquity. A survey of the diet of early peoples. Johns Hopkins University Press. Baltimore. 283 pp.
Civitello, L. 2005. Cuisine and culture. A history of food and people. John Wiley & Sons. Hoboken, New Jersey. 410 pp.
Duarte, A. et al. 2016. Citrus as component of the Mediterranean diet. Journal of Spatial and Organizational Dynamics 4: 289-304.
Estruch Guitart, V. 2007. La citricultura española. Evolución y perspectivas de futuro. Agricultura Familiar en España 2007: 126-140.
FAO. 2017. Citrus fruit – Fresh and procesed. Statistical Bulletin 2016. FAO. Roma.
Faraudo de Saint-Germain, L. 1951-1952. El “Libre de Sent Sovi”. Recetario de cocina catalana medieval. Boletín de la Real Academia de Buenas Letras de Barcelona 24: 5-81.
Hayward, V. 2017. Nuevo Arte de la cocina española de Juan Altamiras. Círculo de Lectores. Barcelona. 493 pp.
Isaac, E. 1959. Influence of religión on the spread of citrus. Science 129: 179-186.
Juderías, A. 1994. Cocina para pobres. Undécima edición. Ed. Seteco. Madrid. 325 pp.
Khoury, C.K. et al. 2016. Origins of food crops connect countries worldwide. Proceedings of the Royal Society B doi: 10.1098/rspb.2016.0792
Langgut, D. 2014. Prestigious fruit tres in ancient Israel: first palynological evidence for growing Junglans regia and Citrus medica. Israel Journal of Plant Sciences doi: 10.1080/07929978.2014.950067
Langgut, D. 2017. The citrus route reveales: From Southeast Asia into the Mediterranean. HortScience 52: 814-822.
Mabberley, D.J. 1997. A classification for edible citrus (Rutaceae). Telopea 7: 167-172.
Mabberley, D.J. 2004. Citrus (Rutaceae): A review of recent advances in etymology, systematics and medical applications. Blumea 49: 481-499.
Pagnoux, C. et al. 2013. The introduction of citrus in Italy, with reference to the identification problems of seed remains. Vegetation History and Archaeobotany DOI: 10.1007/s00334-012-0389-4
Teofrasto. 1988. Historia de las plantas. Ed. Gredos. Madrid. 531 pp.
Toussaint-Samat, M. 2009. A history of food. Wiley-Blackwell. Chichester. UK. 756 pp.
Velasco, R. & C. Licciardello. 2014. A genealogy of the citrus family. Nature Biotechnology 32: 640-642.
Wansink, B. et al. 2016. Food art does not reflect reality: A quantitative content analysis of meals in popular paintings. SAGE Open Doi: 10.1177/215824401654950
Wikipedia. 2019. Citrus. 17 August.
Xu, Q. Et al. 2013. The draft genome of sweet orange (Citrus sinensis). Nature Genetics 45: 59-66.
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo Ingredientes para la receta: Los cítricos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Ingredientes para la receta: El kiwi
- Ingredientes para la receta: El ajo
- Ingredientes para la receta: El conejo
Abril comienza con matemáticas y bromas
En casi todos los países del mundo, el 1 de abril se celebra lo que correspondería a nuestro Día de los inocentes: es el April Fools Day en EE. UU., Reino Unido y algunos otros países; el Día da mentira en Brasil, Le Poisson d’Avril en Francia, el Pesce d’aprile en Italia, el Aprilscherz en Alemania, …
 April Fool’s Day. Imagen: Wikimedia Commons.
April Fool’s Day. Imagen: Wikimedia Commons.Y, ¿por qué se celebra este día? Existen numerosas teorías explicando su origen: algunos lo relacionan con cambio del calendario juliano al gregoriano, otros con el fin de la cuaresma —en el que el pescado era el alimento principal—, también con la apertura de la temporada de pesca e incluso con el signo Piscis del zodiaco. Independientemente de su procedencia, es un día en el que bromas abundan, incluso en el mundo de la ciencia. En la página April Fool’s Day Science Hoaxesse recopilan algunas de estas inocentadas que ayudan a comenzar el mes de abril con sonrisas, también en el ámbito de la ciencia.
Algunas bromas matemáticas del 1 de abril
De entre las muchas bromas matemáticas publicadas en diferentes años celebrando el 1 de abril, destaco algunas de ellas.
El 1 de abril de 1975, el matemático y divulgador Martin Gardner publicaba en la columna Math Games de la revista Scientific American, el artículo titulado Six sensational discoveries that somehow or another have escaped public attention —Seis descubrimientos sensacionales que de alguna manera han escapado a la atención pública— en el que hablaba de algunos sorprendentes descubrimientos científicos. Entre ellos, dos se referían a descubrimientos matemáticos. El primero hablaba sobre un sorprendente resultado obtenido por John Brillo de la Universidad de Arizona, que había descubierto que al elevar el número e al exponente π(163)½ se obtenía el número entero 262.537.412.640.768.744. Y el segundo anunciaba un inesperado descubrimiento realizado por el especialista en teoría de grafos William McGregor: un mapa de110 regionesque precisaba de 5 colores para colorearse —sin que regiones adyacentes compartieran el mismo tono— proporcionando así un contraejemplo a la aún entonces conjetura de los cuatro colores.
El 1 de abril de 2011, Aurélien Alvarez y Michèle Audin publicaron en el sitio Images des mathématiques el artículo titulado Il y a cent quarante ans : la mort de Galois —Haceciento cuarentaaños: la muerte de Galois—. Los dos matemáticos explicaban que el día 3 de abril de 1871, Galois salía de su casa tras haber finalizado la prueba de un teorema, y caía abatido por una bala durante las revueltas de la Comuna de París. Galois fallecía así con 60 años… La broma sobre la fecha del fallecimiento de Évariste Galois (1811-1832) iba acompañada por una extensa explicación matemática sobre el teorema que supuestamente Galois había demostrado, y una imagen del matemático poco tiempo antes de fallecer.
Ese mismo año, en su blog Freakonometrics, Arthur Charpentier publicaba el 1 de abril el artículo titulado Fin des débats sur la valeur de π –Fin de los debates sobre el valor de π-. El matemático comentaba que la Unión Matemática Internacional había decidido que, a partir del día 1 de julio de 2011, el valor de π sería oficialmente igual a 4. ¿La razón? Evitar un “colapso informático sin precedentes” debido a la continua investigación sobre los decimales de π, cuya velocidad superaba los avances del software Windows…
Y no olvidemos al siempre ocurrente Matthew Weathers de la Biola University que regala a su alumnado cada 1 de abril con una emocionante lección de matemáticas. Debajo puede disfrutarse de una de ellas, aunque hay algunas más en su canal de YouTube.
La primera de ellas es Sophie Germain (1776-1831), quien realizó importantes aportaciones a la teoría de números y la teoría de la elasticidad. Los números primos de Germain se nombraron en su honor, ya que esta matemática demostró que el Último teorema de Fermat se cumplía para estos primos. Recordemos qu en Mudanza de nombre, el escritor Eduardo Galeano realizaba una hermosa semblanza de Sophie Germain.
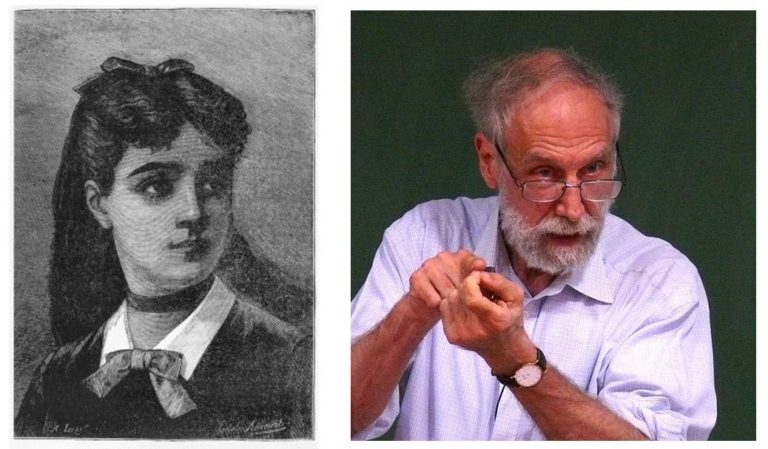 Sophie Germain y Alain Connes. Imágenes: Wikimedia Commons.
Sophie Germain y Alain Connes. Imágenes: Wikimedia Commons.Y quería destacar también a Alain Connes (1947), la primera persona a la que pedí un autógrafo. Recuerdo que fue en 1991 durante The Symposium on the Current State and Prospects of Mathematics realizado en Barcelona y al que tuve la suerte de asistir. En este simposio, siete Medallas Fields —René Thom, Sergei Novikov, Shing-Tung Yau, Alain Connes, Stephen Smale, Vaughan Jones y Gerd Faltings— explicaban las claves de su trabajo. En esa época realizaba mi tesis doctoral centrada precisamente en la resolución de la conjetura de Baum-Connes en un tipo especial de espacios foliados. Muy amable, Connes me escribió una cálida dedicatoria en mi ejemplar de su Géométrie non commutative (InterEditions, 1990)…
¡Feliz 1 de abril! Por mi parte, desde casa, dedicaré un ratito a intentar detectar alguna de esas bromas matemáticas con las que nos suelen regalar en esta fecha.
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo Abril comienza con matemáticas y bromas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El teorema de los cuatro colores (1): una historia que comienza en 1852
- La extraordinaria capacidad poética de las matemáticas
- Las dos culturas de las matemáticas: construir teorías o resolver problemas
Tipos de comportamiento conductor
 Foto: Israel Palacio / Unsplash
Foto: Israel Palacio / UnsplashLa investigación sobre la electricidad y el comportamiento de las corrientes eléctricas [1] permitió el enorme crecimiento y la extensión de la era eléctrica en la que vivimos hoy. La energía eléctrica es la forma dominante de consumo de energía en los países industrializados y es un elemento esencial en el funcionamiento de muchos de los dispositivos que usamos todos los días. Durante décadas, una de las propiedades menos entendidas pero más prácticas de un trozo de materia sólida fue su capacidad o no de conducir la electricidad.
¿Por qué algunos materiales conducen electricidad, otros actúan como aislantes y otros (como los semiconductores) actúan como uno u otro según las condiciones? ¿Podría una mejor comprensión del fenómeno aumentar sus aplicaciones prácticas? [2]
Georg Ohm descubrió una ley empírica, conocida como la ley de Ohm, que relaciona la corriente en un material y el voltaje aplicado al material: V = IR. Aquí V es la diferencia de potencial, I es la corriente (o intensidad) y R es la resistencia del material. La resistencia es normalmente constante para cada material, pero hay un valor de la resistencia distinto para cada material. A medida que aumenta la resistencia de un material, su conductividad disminuye, por lo que la cantidad de corriente que conduce también debe disminuir, de acuerdo con la ley de Ohm: I = V/R.
Por tanto, si la resistencia de un material es tan grande que se aproxima a infinito, entonces V/R se hace prácticamente cero, y nos encontramos con que I = 0. Esto significa que no fluye corriente a través del material. Esto es lo que observamos en esos materiales que llamamos aislantes. Un aislante, a efectos prácticos [3], no permite el paso de corriente eléctrica.
Por otro lado, si R se pudiese hacer cero, la corriente sería infinita [4], incluso para el voltaje más pequeño. Esto es lo que sucede en un superconductor. Incluso sin una fuente de voltaje, una corriente en un bucle hecho de material superconductor, una vez iniciada continuará sin alteraciones indefinidamente [5][6].
En un conductor normal la corriente desaparece en una pequeña fracción de segundo sin la ayuda de un voltaje externo. Incluso con un voltaje externo aplicado, sabemos que un cable de resistencia normal, de cobre, por ejemplo, por el que circula una corriente comienza a calentarse, lo que indica que la energía eléctrica se está convirtiendo en energía térmica [7].
Este comportamiento es similar a la conversión de energía cinética en energía térmica debido a la fricción, como cuando frotas las manos para calentarlas. Esto sería indicio de que tal vez la corriente en un cable no superconductor encuentra un tipo de fricción a medida circula por el cable, lo que explicaría por qué el cable se calienta. Esto sugiere que en un aislante habría tanta fricción interna que no permite que fluya ninguna corriente, mientras que los superconductores no tendrían fricción, lo que permite que las corrientes fluyan indefinidamente sin ninguna pérdida notable de energía.
Nuestros modelos de sólidos cuánticos, si son válidos, deberían poder explicar la ley de Ohm y los distintos tipos de comportamiento conductor que acabamos de describir.
Notas:
[1] Véase nuestra serie Electromagnetismo
[2] Esta última es una pregunta casi retórica. El mero hecho de que puedas leer esto es una respuesta afirmativa. Pero ya llegaremos a eso.
[3] Eso no significa que no pueda pasar corriente por un aislante. Por muy grande que sea la resistencia si la diferencia de potencial es lo suficientemente grande pasará una corriente medible. Estamos pues en el mismo caso que con los venenos, una sustancia lo será o no dependiendo de la dosis. Un material será aislante o no dependiendo de la relación entre su resistencia, finita por muy grande que sea, y la diferencia de potencial aplicada de forma efectiva.
[4] Matemáticamente hablando, indefinida.
[5] Como la corriente I es carga por unidad de tiempo el hecho de que sea “infinita” realmente lo que implica es que es “eterna”, porque las cargas presentes son finitas, son las que son. Piénsalo un poco, porque el razonamiento no es tan simple.
[7] Los cables pueden calentarse tanto que pueden llegar a emitir luz. Dependiendo del material y sus resistencia las temperaturas alcanzadas son tales que pueden emitir luz, por ejemplo, en prácticamente todo el espectro visible, y esto se usa(ba) en las bombillas de filamento incandescente, o básicamente en el rojo e infrarrojo, y esto se usa en las calefacciones eléctricas.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Tipos de comportamiento conductor se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Tipos de materia sólida
- El comportamiento corpuscular de la luz: momento lineal del fotón
- El comportamiento corpuscular de la luz: el efecto Compton
No todo vale al servicio de la ciencia
 Foto: Alev Takil / Unsplash
Foto: Alev Takil / UnsplashExperimentación con seres humanos
El primer ejemplo conocido de experimentación con seres humanos fue el de Edward Jenner, cuando inoculó a una niña de ocho años de edad el pus tomado de viruela de ganado. El experimento de Jenner resultó un éxito y abrió la era de las vacunas pero, curiosamente, hoy resultaría inaceptable. Y antes de la abolición de la esclavitud en los Estados Unidos, no era infrecuente que los médicos comprasen esclavos negros para experimentar con ellos, realizando dolorosísimas y peligrosas intervenciones.
Fue en pleno siglo XX y en el contexto de la II Guerra Mundial, cuando se llegó a experimentar a gran escala con seres humanos. Como es de sobra conocido, médicos nazis realizaron experimentos atroces con prisioneros de campos de concentración (efecto de la hipoxia, efectos del gas nervioso, congelaciones, efectos de las altas presiones e ingestión de agua de mar). En Nürenberg 23 médicos fueron llevados a juicio por esas atrocidades.
Menos conocidos que los experimentos en los campos de concentración alemanes son los que realizaron los investigadores de la Unidad 731 del ejército japonés durante su ocupación de China y Manchuria durante los años 30 y 40. La Unidad 731 era de guerra química y biológica, y los experimentos, que incluían vivisecciones y provocaron la muerte de miles de prisioneros de diferentes nacionalidades, tenían como objetivo desarrollar técnicas para expandir y prevenir los efectos de agentes químicos y biológicos propios de esa modalidad bélica. En ellos colaboraron médicos y científicos, y al contrario de lo que ocurrió con los alemanes que fueron juzgados en Nürenberg, se les ofreció inmunidad a cambio de la información que poseían, información en la que estaban muy interesados científicos norteamericanos.
Entre 1963 y 1966 investigadores de la Willowbrook School de Nueva York hicieron ingerir a niños con retraso mental virus de la hepatitis vivos para estudiar la etiología de la enfermedad y la posibilidad de elaborar una vacuna.
En 1963, médicos del Hospital Judío de Enfermedades Crónicas de Brooklyn inyectaron células cancerosas vivas a pacientes ancianos sin informarles al respecto, para estudiar las respuestas inmunitarias del organismo.
En 1972 se dio a conocer que el Servicio de Salud Pública de los EEUU había desarrollado el “experimento de la sífilis de Tuskegee”, una investigación de larga duración. En ese estudio hombres afroamericanos en estadios avanzados de sífilis habían sido sometidos a experimentación sin haber garantizado que se había obtenido su consentimiento informado.
Lo que expondremos a continuación no tiene la gravedad de las actuaciones reseñadas en los párrafos anteriores, pero se trata de una práctica que se encuentra en el límite de lo admisible. Por otro lado, quizás no es del todo apropiado considerarlas como actividades al servicio de la ciencia, pero entendemos que debe figurar aquí porque, al fin y al cabo, en ella se hallan implicados médicos y científicos. Nos referimos a lo que podría denominarse, eufemísticamente, “deslocalización” de ensayos clínicos.
A lo largo de lo que llevamos de siglo, una parte importante de la investigación clínica se ha trasladado a países pobres. Ello puede haber sido debido a regulaciones cada vez más estrictas en los países desarrollados en lo relativo a la protección de las personas sujeto de los experimentos. También puede deberse a que los procedimientos se han hecho más costosos y burocratizados. Por otro lado, en los países más pobres pueden aplicarse variantes más flexibles de los protocolos de investigación. Los comités éticos son más permisivos. Los riesgos jurídicos, con las consiguientes indemnizaciones son menores de manera que los costes de los seguros también lo son. Es también más fácil contar con voluntarios para participar en ensayos clínicos. Todo ello ha conducido a que se usen estándares éticos diferentes en los países pobres y en los desarrollados.
15 ensayos clínicos en varios países africanos y República Dominicana han sido acusados de no respetar los estándares éticos exigibles. Se refiere a estudios que demostraron que suministrando AZT a mujeres embarazadas VIH-positivas y a los bebés durante 6 semanas tras el nacimiento, reducía la transmisión perinatal de VIH de un 25% a un 8%. La acusación se basó en haber mantenido un grupo control (placebo). La diferencia entre haberlo hecho con o sin placebo radicaba en la magnitud, coste y duración de los ensayos, mucho más largos y caros de no haber utilizado un grupo de placebo.
En general son muy problemáticos los ensayos hechos en países pobres: se utiliza a personas que no reciben una parte de los beneficios que proporcionan los ensayos.
Experimentación con animales
La experimentación con animales es una cuestión controvertida. Hay personas que se oponen radicalmente al uso de animales en investigación invocando argumentos de carácter ético. Sin embargo, los defensores de este tipo de investigaciones invocan la primacía del bienestar y dignidad humanas como razón para justificar su práctica, sobre todo en áreas en que se persiguen mejoras significativas en la salud humana.
La experimentación con animales tiene una larga historia que se remonta, al menos, hasta el Renacimiento. William Harvey, el descubridor de la circulación general, fue uno de los primeros, y lo justificó aduciendo que estudiando diferentes animales se podía aprender cómo funcionaba el ser humano. Y ya en el siglo XIX, son conocidísimos los experimentos con animales de Claude Bernard, experimentos que él justificaba abiertamente. En la actualidad los experimentos con animales persiguen diferentes propósitos; buscan conocer la propia biología de los animales, pero también se utilizan porque no se pueden usar seres humanos en cuestiones que nos afectan o interesan; en cierto modo son nuestros sustitutos. Los utilizamos como modelo en ensayos de fármacos y, en general, de tratamientos médicos.
La mayor parte de los laboratorios en que se trabaja con animales se encuentran en países en los que rigen normas y códigos de conducta que determinan qué prácticas son aceptables y cuáles no. Tales regulaciones persiguen disminuir el número de animales utilizados -en mayor medida cuanto más próximos se encuentren a los seres humanos- y también reducir el dolor y sufrimiento hasta los mínimos estrictamente necesarios.
En España, además de las normas legales que todos los laboratorios están obligados a cumplir, las sociedades científicas (COSCE) han impulsado un Acuerdo de transparencia sobre el uso de animales en experimentación científica. El acuerdo consiste en un documento que busca “establecer vías de comunicación entre la comunidad científica y la sociedad sobre cuándo, cómo y por qué se usan animales en investigación y los beneficios que se derivan de esta práctica”. Más de 80 instituciones (entre las que se encuentran organismos públicos de investigación como el CSIC; varias universidades; centros de investigación como CNIO y CNIC, sociedades científicas como SEBBM, SENC, empresas y hospitales) han suscrito el acuerdo, en virtud del cual se comprometen a “compartir información de forma transparente, y fomentar la comunicación acerca de la investigación con animales para hacer llegar al público toda la información sobre las razones, los métodos y el avance en el conocimiento que la misma genera y que justifica el uso de animales en investigación científica.”
Fuentes:
Además de las enlazadas en el texto, las fuentes utilizadas han sido los artículos de la Encyclopedia of Applied Ethics referenciados a continuación:
Briggle, A (2012): Scientific Responsability and Misconduct, in Encyclopedia of Applied Ethics, Vol 4, pp.: 41-48, 2nd edition, Academic Press, London
Johnson, S (2012): Nanotechnology, in Encyclopedia of Applied Ethics, Vol III, pp.: 183-185, 2nd edition, Academic Press, London
Resnik, D B (2012): Developing World Bioethics, in Encyclopedia of Applied Ethics, Vol 1, pp.: 771-778, 2nd edition, Academic Press, London
Solbakk J H, Vidal, S M (2012): Research Ethics, Clinical, in Encyclopedia of Applied Ethics, Vol 3, pp.: 775-785, 2nd edition, Academic Press, London
Spier, R E (2012): Science and Engineering Ethics, Overview, in Encyclopedia of Applied Ethics, Vol 4, pp.: 14-31, 2nd edition, Academic Press, London
Este artículo se publicó originalmente en el blog de Jakiunde. Artículo original.
Sobre los autores: Juan Ignacio Perez Iglesias es Director de la Cátedra de Cultura Científica de la UPV/EHU y Joaquín Sevilla Moroder es Director de Cultura y Divulgación de la UPNA.
El artículo No todo vale al servicio de la ciencia se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:El futuro es inescrutable, sus amenazas también lo son
 Foto: Louis Reed / Unsplash
Foto: Louis Reed / UnsplashEn 1971, dos años después de haber sido elegido presidente de los Estados Unidos, Richard Nixon firmó la denominada National Cancer Act, una ley mediante la que se proponía acabar con el cáncer. Aunque la ley en cuestión no la recogía en su tenor literal, la expresión “guerra al cáncer” fue profusamente utilizada para referirse al plan federal de actuaciones. Junto con otras medidas, se destinaron al plan 1.500 millones de dólares y Nixon prometió que lo “derrotarían”.
Otros gobiernos, el español incluido, declaran ahora la “guerra” a otra enfermedad, la provocada por el coronavirus SARS-CoV-2. Además de las medidas implantadas para contener la expansión de la pandemia, los planes contienen actuaciones de política científica, con una importante inyección de recursos económicos para investigar sobre el coronavirus y posibles tratamientos para “vencerlo”.
En medio de tanta zozobra, dolor e incertidumbre como está causando la pandemia, gobernantes y prescriptores de opinión parecen depositar su confianza en la ciencia como instrumento para resolver el reto más formidable que afrontan generaciones. Porque parece haber calado la idea de que, como decíamos hace dos semanas, solo el conocimiento permitirá superarlo.
Conviene, no obstante, ser cautos. El pasado lunes 23 la revista Science publicó un editorial en el que advertía del riesgo de que se le pida demasiado a la ciencia o de que, incluso, la propia comunidad científica genere más expectativas de las debidas. El editorial utilizaba, a tal efecto, el caso del VIH: fueron necesarias décadas de esfuerzo en virología, epidemiología y desarrollo de nuevos fármacos para empezar a obtener resultados. Y si bien es cierto que desde hace tiempo el SIDA se ha convertido en una enfermedad crónica, tan solo ahora, cuatro décadas después, están empezando a curarse algunos enfermos.
Algo parecido cabe decir de las investigaciones sobre el cáncer y sus resultados. Hoy sabemos más sobre los procesos implicados en las diferentes enfermedades que se engloban bajo esa denominación, y desde 1971 se han hecho progresos en el conocimiento de cuestiones tales como los factores de riesgo, los tratamientos y la prognosis de algunos tipos. Pero muchos siguen siendo incurables y la mortalidad se ha reducido solo levemente desde entonces. Recuperando la metáfora bélica, el cáncer sigue sin haber sido “derrotado”.
El contraejemplo de esas “guerras” es el proyecto Manhattan -este sí, de carácter bélico-, que se saldó con la producción de la bomba atómica. La comunidad científica contaba con suficiente conocimiento acerca de la estructura del átomo y la naturaleza de la materia. Y eso permitió a los norteamericanos disponer, en tiempo récord, del arma más mortífera que ha creado la humanidad.
Es importante, por supuesto, que se destinen recursos a la investigación sobre coronavirus y sobre epidemias en general. Pero la conclusión que cabe extraer de lo anterior debe llevarnos más allá.
No sabemos qué nos deparará el futuro. Si bien es cierto que algunos peligros posibles son demasiado probables como para ignorarlos, también lo es que otros son completamente impredecibles, de la misma forma que desconocemos en qué materias o en qué campos necesitaremos generar conocimiento en el futuro próximo. También ignoramos aspectos fundamentales que subyacen a algunos de los problemas del presente, como pone de manifiesto la historia del cáncer. Por eso, la estrategia más útil consiste en aumentar y diversificar el esfuerzo, sembrando en terrenos diferentes, porque desconocemos hoy lo que necesitaremos mañana. Es importante atesorar conocimiento en materias diversas porque cuanto más sepamos, mejor pertrechados estaremos para hacer frente a los retos que, en forma de pandemias o de cualquier otra naturaleza, esperan a la humanidad.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo El futuro es inescrutable, sus amenazas también lo son se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:¡Leamos poesía astronómica en las rocas!
Los fósiles, los minerales o las rocas son, entre otras cosas, en lo primero que pensamos al hablar de geología, pero lo cierto es que la física es un ámbito científico que difícilmente se puede desvincular de la geología. Y es que el fundamento físico resulta clave a la hora de explicar algunos procesos geológicos que suceden tanto en el océano como en la superficie terrestre.
Con el fin de poner sobre la mesa la estrecha relación entre la geología y la física, los días 27 y 28 de noviembre de 2019 se celebró la jornada divulgativa “Geología para poetas, miopes y despistados: La Geología también tiene su Física”. El evento tuvo lugar en la Sala Baroja del Bizkaia Aretoa de la UPV/EHU en Bilbao.
La segunda edición de esta iniciativa estuvo organizada por miembros del grupo de investigación de Procesos Hidro-Ambientales (HGI) de la Facultad de Ciencia y Tecnología de la Universidad del País Vasco, en colaboración con el Vicerrectorado del Campus de Bizkaia, el Geoparque de la Costa Vasca y la Cátedra de Cultura Científica de la UPV/EHU.

En las rocas se puede leer la historia climática de la Tierra. Pero si se hace con los ojos de un poeta y se busca inspiración en la astronomía te encuentras con que puedes leer poesía en las rocas, como los que explica Aitor Payros, profesor del departamento de estratigrafía y paleontología de la Universidad del País Vasco.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo ¡Leamos poesía astronómica en las rocas! se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Las mareas del pasado leídas en las rocas del presente
- Terremotos en la gran pantalla: algunas verdades y diversas mentiras
- La eternidad en un grano de arena
La supervivencia siempre tiene un coste: la prevalencia del haplogrupo H en Europa
 Esqueleto de uno de los individuos enterrados en la necrópolis de la ermita de San Miguel de Ereñozar. Foto: Mikel Neira.
Esqueleto de uno de los individuos enterrados en la necrópolis de la ermita de San Miguel de Ereñozar. Foto: Mikel Neira.Entre el siglo XIV y el XIX se produjo un período de inestabilidad climática conocido como la Pequeña Edad de Hielo que afectó principalmente al hemisferio norte. Durante este período se produjo un incremento de la actividad tormentosa y un descenso de la temperatura, que, aunque no fue muy severo, entre 1º y 2ºC, tuvo consecuencias devastadoras. El clima benigno de siglos anteriores, que había provocado un aumento notable de la población, se transformó en otro más duro y conllevó la destrucción de cosechas, la muerte de animales y, en definitiva, hambre. Y con las hambrunas, la salud de las poblaciones se debilitó y se propagaron las enfermedades. Basta recordar la pandemia de peste negra que asoló Europa en el siglo XIV, acabando con aproximadamente un tercio de su población.
¿Influyeron ese cambio climático y las consiguientes enfermedades en la genética humana? En la población europea actual el linaje del ADN mitocondrial, es decir, el material genético que se transmite por vía materna, más frecuente es el H. ¿Por qué?
 Reconstrucción del Castillo-Ermita de San Miguel de Ereñozar en época medieval. Fuente: Urdailife. Abajo, vídeo con el estado actual y la ubicación de la ermita.
Reconstrucción del Castillo-Ermita de San Miguel de Ereñozar en época medieval. Fuente: Urdailife. Abajo, vídeo con el estado actual y la ubicación de la ermita.
En el yacimiento medieval de San Miguel de Ereñozar el grupo de Biología Evolutiva Humana de la Facultad de Ciencia y Tecnología de la UPV/EHU, ha encontrado elementos que podrían servir para esclarecerlo. En esa necrópolis de la comarca vizcaína de Busturialdea-Urdaibai, en uso del siglo XIII al XVI, hay enterrados 163 individuos, de los que un 73% pertenecen al haplogrupo H, una frecuencia más alta que la que se da hoy en día en Europa.
“En la bibliografía ya se había postulado que algunos linajes mitocondriales podrían tener una relación con diferentes tipos de enfermedades y además, presentar un comportamiento diferencial con respecto al desarrollo de las mismas”, explica Imanol Martín, quien ha desarrollado la investigación como parte de su tesis. Así, los haplogrupos J y T protegerían frente al desarrollo de la osteoartritis, mientras que el haplogrupo H incrementaría el riesgo a desarrollar enfermedades reumáticas.
Así, que los investigadores de la UPV/EHU buscaron manifestaciones reumáticas en los esqueletos de los 163 individuos enterrados en Ereñozar, y los encontraron en 47. Y, puesto que para que las enfermedades reumáticas dejen signos óseos es necesario que pase el tiempo, se eligieron los restos de otras 43 personas de más de 45 años de edad de la misma necrópolis como grupo de control. En ambos grupos se llevaron a cabo análisis de los distintos linajes mitocondriales. “El haplogrupo H fue más frecuente entre los individuos con manifestaciones reumáticas que en el grupo control y, a su vez, fue este haplogrupo mitocondrial el más frecuente entre los individuos afectados con espondiloartritis (grupo de enfermedades reumáticas e inflamatorias de las articulaciones)”, añade Martín.
En definitiva, el estudio confirma la relación entre las enfermedades reumáticas y el haplogrupo H, y también da pistas sobre la elevada frecuencia de este haplogupo en la población europea: “En esa época de déficit de alimentos los individuos del haplogrupo H tenían una ventaja selectiva frente a los que tuvieran otros haplogrupos, ya que el H es más eficiente a la hora de obtener energía de la dieta”. Sin embargo, ese metabolismo altamente eficiente también genera las llamadas especies reactivas de oxígeno (radicales libres, iones de oxígeno…), que desencadenan la disfunción y apoptosis celular y provocan, a la larga, la degradación del cartílago y el desarrollo de enfermedades de carácter reumático. La supervivencia siempre tiene un coste.
Referencia:
I.M. Laza, M. Hervella, M. Neira Zubieta & C. de-la-Rúa (2019) Environmental factors modulated ancient mitochondrial DNA variability and the prevalence of rheumatic diseases in the Basque Country Scientific Reports doi: 10.1038/s41598-019-56921-x
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo La supervivencia siempre tiene un coste: la prevalencia del haplogrupo H en Europa se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Fotovoltaicos siempre a máxima potencia
- El planeta enano Haumea tiene anillo
- La selección positiva de la piel clara en el sur de Europa
Lienzos y partituras para crear nuevas vacunas
![]()
José de la Fuente, Juan José Pastor Comin y Sara Artigas Jerónimo
 “El beso”, de Israel León Viera, que representa la nueva e inexplorada interacción de AKR con AKR o de SUB con SUB.
“El beso”, de Israel León Viera, que representa la nueva e inexplorada interacción de AKR con AKR o de SUB con SUB.KGJ Colección, Author provided
¡Que suene la música! La trucha alpina al oboe. Una rana al clarinete. El fagot para la mosca del vinagre. La única persona de esta peculiar banda toca el violín, mientras que una garrapata se encarga de la viola. Completa el sexteto de viento y cuerda un Caenorhabditis elegans, un pequeño gusano de un milímetro que hará que suene un imponente chelo.
¿Puede un compositor procurar una banda sonora que transcriba los datos que emergen de la rutina experimental de tubos de ensayo y probetas? Todos los componentes de la banda tienen algo en común: una proteína en su ADN. ¿Puede la información genética trasladarse a una partitura?
 Secuencias de AKR/SUB dispuestas polifónicamente. Recurrencias y motivos.
Secuencias de AKR/SUB dispuestas polifónicamente. Recurrencias y motivos.Juan José Pastor., Author provided
La ciencia consiste en plantear nuevos interrogantes. Innovar es romper con lo establecido ¿Pueden el arte y la música ayudarnos a comprender la respuesta de nuestro organismo a una infección? ¿Y si los diseños de los artistas plásticos pudieran recoger sobre un lienzo los caminos que la ciencia debe abordar en el diseño de nuevos experimentos? ¿Podría una composición musical ayudar a entender con el comportamiento de sus voces, sus líneas melódicas, su forma y su estructura, las interacciones de las proteínas cuando estas responden ante la amenaza de un nuevo patógeno?
Para responder a esto tenemos que abrir nuestra mente. Y experimentar.
Científicos y artistas
Investigadores del área de Genómica, Proteómica y Biotecnología del grupo SaBio en el Instituto de Investigación de Recursos Cinegéticos, centro mixto de la Universidad de Castilla-La Mancha y el CSIC, hemos desarrollado a través de un equipo interdisciplinar de científicos, artistas y músicos una nueva metodología. Esta nueva aproximación, publicada en el último número de la revista Vaccines, reúne el enfoque artístico y científico en la caracterización de la akirina (AKR), una proteína también conocida como subolesina (SUB) en garrapatas, para avanzar en el estudio del papel que juegan estas moléculas en la regulación de la respuesta inmune.
De esta forma, se identifican los mecanismos y genes que son expresados en nuestras células y se convierten en proteínas con un papel funcional en respuesta a la infección. Estas proteínas están muy conservadas a través de la evolución en distintas especies y han sido eficaces en el desarrollo de vacunas. Este conjunto de proteínas interactúa física y funcionalmente entre ellas en respuesta a algún estímulo, como podría ser su comportamiento ante una infección en células humanas.
La colaboración entre científicos y artistas proporcionó dos resultados:
- Un algoritmo que utiliza conjuntos musicales, basados en la akirina y secuencias de proteínas que interactúan, como un nuevo método para caracterizar la evolución y las interacciones entre proteínas.
- La sugerencia de artistas visuales de propiedades previamente inexploradas.
Este planteamiento proporciona un enfoque combinado para comprender algunas de las preguntas desafiantes de la biología molecular.
Del ADN a la partitura
Tradujimos las secuencias del ADN de la akirina de distintas especies animales a motivos musicales. Para ello utilizamos un primer algoritmo modificado que atendía a la altura y el ritmo. Esto permitió generar el patrón melódico de cada especie animal y su configuración motívica, y también observar las similitudes presentes entre las secuencias en distintas especies y la identificación de los motivos repetidos.
La representación musical no solo permitió una comprensión lineal –-melódica-– de la singularidad de cada especie estudiada, sino que permitió su visión polifónica –conjunta y simultánea-–, como una composición compleja y lógica. El análisis del contrapunto –cómo unas voces o especies se imitan unas a otras-– aportó una textura musical llena de correspondencias, que se mostraba viva a través del sonido.
Ciencia sobre lienzo
En el caso de la pintura, trasladamos al artista una hipótesis científica de partida que sirvió al pintor para expresar un problema biológico sobre los materiales artísticos elegidos y que este tratara de resolverlo a través de formas, composición, trazos y color sobre la tela y el bastidor.
Esta contribución creativa nos ayudó a representar su propia teoría de una forma original y desde un punto de vista completamente diferente, no conceptual, lejos de la organización estadística de los datos recogidos.
La nueva representación visual constituye un nuevo contexto de referencias aperturista que estimula la imaginación y la creatividad y que permite establecer nuevas hipótesis que, a la única luz de los datos experimentales obtenidos, tal vez no hubieran surgido. La representación artístico-visual sirvió no solo para identificar problemas conocidos en las formas de expresión de un lenguaje artístico, sino también para suscitar nuevas ideas divergentes.
 KGJ Colección, Ciudad Real, España., Author provided
KGJ Colección, Ciudad Real, España., Author providedLos resultados mostraron de un modo plural e interdisciplinar que la interacción entre varías moléculas de AKR y SUB y las interacciones físicas con diferentes proteínas simultáneamente están involucradas en la regulación de varios procesos biológicos. Además, ayudaron a entender, a través de estas nuevas formas de representación artística y musical, el papel de las interacciones estudiadas en la regulación positiva y negativa de respuesta inmune. Así entendimos cómo se activa o suprime la expresión de algunos genes concretos.
¿Qué implicaciones alcanza esta colaboración? No solo contribuye a la investigación, sino que puede lograr el desarrollo de vacunas para el control de infestaciones por garrapatas, así como para el estudio de patógenos transmitidos por estas.
Este puede ser un avance esencial en contextos de exclusión social en un mundo que cuenta con un importante índice poblacional situado bajo el umbral de pobreza. Ahí es donde científicos y artistas pueden avanzar juntos y de la mano, iluminando el avance de la investigación ante los nuevos desafíos científicos que permitan construir un mundo mejor.![]()
Sobre los autores: José de la Fuente es profesor de investigación en el Instituto de Investigación en Recursos Cinegéticos (CSIC – Universidad de Castilla-La Mancha) y profesor adjunto en el departamente de patobiología veterinaria de la Universidad Estatal de Oklahoma (Estados Unidos); Juan José Pastor Comin es es profesor titular del área de Música en la Universidad de Castilla-La Mancha y co-director del Centro de Investigación y Documentación Musical (CIDoM); Sara Artigas Jerónimo es investigadora predoctoral en el Instituto de Investigación en Recursos Cinegéticos.
Este artículo fue publicado originalmente en The Conversation. Artículo original
El artículo Lienzos y partituras para crear nuevas vacunas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Dudas sobre las vacunas: problemas y soluciones
- Nuevas tecnologías para el estudio del cerebro: Desde Cajal a nuestros días
- Desmitificando: Vacunas peligrosas
La cuadratura del cuadrado: las redes eléctricas de Kirchhoff
En mi anterior entrada del Cuaderno de Cultura Científica La cuadratura del cuadrado: en busca del santo grial estuvimos hablando de un hermoso rompecabezas matemático, el problema de la cuadratura perfecta del cuadrado, que recuerdo a continuación:
Problema de la cuadratura perfecta del cuadrado (o rectángulo): Dividir un cuadrado (o rectángulo) en un número finito de cuadrados más pequeños, todos de distintos tamaños.
Este problema, que durante mucho tiempo se pensó que no tenía solución para cuadrados, lo que se conoció como la conjetura de Luzin, fue finalmente resuelto en positivo, alrededor del año 1939, por dos grupos de matemáticos. Por una parte, el matemático alemán Roland P. Sprague (1894-1967) construyó un cuadrado con una cuadratura perfecta, pero compuesta (recordemos que eso significa que contiene la cuadratura de algún sub-rectángulo), de orden 55. Mientras que los cuatro estudiantes del Trinity College de la Universidad de Cambridge (Reino Unido), Rowland L. Brooks (1916-1993), Cedric A. B. Smith (1917-2002), Arthur H. Stone (1916-2000) y William Th. Tutte (1917-2002), consiguieron construir el primer cuadrado perfecto simple (no compuesto), también de orden 55. Para ello, los cuatro de Trinity (puede leerse más sobre ellos en la entrada Blanche Descartes y la cuadratura del cuadrado) relacionaron el problema de las disecciones cuadradas de los rectángulos, en particular, de los cuadrados, con la teoría de las redes eléctricas de Kirchhoff, que es de lo que vamos a hablar en esta entrada.
 Una de las ocho cuadraturas perfectas simples del cuadrado de orden 22 que existen. Imagen de la página Tiling by squares, de Stuart Anderson
Una de las ocho cuadraturas perfectas simples del cuadrado de orden 22 que existen. Imagen de la página Tiling by squares, de Stuart AndersonComo explicamos en la anterior entrada, La cuadratura del cuadrado: en busca del santo grial, el primer acercamiento de los jóvenes estudiantes de Cambridge, Brooks, Smith, Stone y Tutte, fue experimental. Intentaron construir mediante una sencilla técnica algebraica algún ejemplo de disección de un cuadrado en cuadrados más pequeños de diferentes tamaños. Con esta técnica sí consiguieron construir algunos ejemplos de cuadraturas perfectas de rectángulos, pero no de cuadrados. Este método experimental dependía demasiado de la suerte y podrían no encontrar nunca el ansiado grial, una cuadratura perfecta del cuadrado. Era como encontrar una aguja en un pajar, sin saber además si había aguja. Por este motivo, abandonaron el camino experimental a favor de un enfoque más teórico, que además les permitiera conocer más sobre el problema.
Entonces, empezaron a asociar diferentes tipos de diagramas a las cuadraturas de los rectángulos. Hasta que llegaron a un diagrama propuesto por Cedric Smith, que sus compañeros no dudaron en llamar el “diagrama de Smith”, que asociaba cada cuadratura de un rectángulo con el grafo de una red eléctrica.
Para ilustrar la construcción de la red eléctrica asociada a una cuadratura, consideraremos el ejemplo de la división de un rectángulo de dimensiones 32 x 33 en 9 cuadrados de distintos tamaños, de lados 1, 4, 7, 8, 9, 10, 14, 15 y 18, luego de orden 9, obtenida por el matemático polaco Zbigniew Moron en 1925, que aparece en la siguiente imagen. Cada segmento horizontal se representará como un vértice del grafo y dos vértices estarán unidos mediante una arista si existe un cuadrado que tiene su lado superior apoyado en el segmento horizontal correspondiente a uno de los vértices y su lado inferior apoyado en el segmento horizontal del otro vértice. Además, el grafo está dirigido, como se muestra mediante las fechas de las aristas, de arriba hacia abajo, que es el orden de la corriente eléctrica, del polo positivo (que consideramos el vértice del lado horizontal superior) al polo negativo (el vértice del lado horizontal inferior). Más aún, es un grafo etiquetado, ya que asociamos a cada arista el valor del lado del cuadrado correspondiente, que será el valor de la corriente eléctrica.
 Diagrama de Smith de la cuadratura perfecta del rectángulo de dimensiones 32 x 33 en 9 cuadrados de distintos tamaños, de lados 1, 4, 7, 8, 9, 10, 14, 15 y 18
Diagrama de Smith de la cuadratura perfecta del rectángulo de dimensiones 32 x 33 en 9 cuadrados de distintos tamaños, de lados 1, 4, 7, 8, 9, 10, 14, 15 y 18
Lo curioso es que el diagrama de Smith cumple las leyes de Kirchhoff para las redes eléctricas, asumiendo que la resistencia de cada arista es igual a 1. La primera ley de Kirchhoff establece que en cada nodo (vértice) del circuito eléctrico, con excepción de los polos, la suma de las corrientes debe ser cero, es decir, la suma de las corrientes que entran en el nodo es igual a la suma de las corrientes que salen del mismo. Por ejemplo, si miramos a la red eléctrica anterior, en el primer vértice después del polo positivo, entra una corriente de 14 y salen dos de 10 y 4, o en el siguiente entran dos corrientes de 4 y 18, mientras que salen dos corrientes de 7 y 15. Esto es debido a que, en un segmento horizontal (vértice) cualquiera de la cuadratura del rectángulo, la suma de los lados de los cuadrados que se apoyan en el segmento desde arriba (la suma de las corrientes que entran) es igual a la suma de los lados de los cuadrados que se apoyan en el segmento desde abajo (la suma de las corrientes que salen), que en ambos casos es la longitud del segmento horizontal.
Teniendo en cuenta que, por la ley de Ohm de los circuitos eléctricos, la diferencia de potencial de cada arista del circuito es igual al producto de la resistencia, que en este caso hemos asumido que es 1, por la corriente, ambas –diferencia de potencia y corriente- son iguales. Por lo tanto, la segunda ley de Kirchhoff establece que la suma algebraica de las corrientes –diferencias de potencial- de cualquier circuito cerrado es cero. En el ejemplo de arriba, en el primer circuito cerrado tenemos que 14 + 4 – 18 = 0 o en el segundo 10 + 1 – 7 – 4 = 0. Esto es debido a que cada segmento vertical de la cuadratura del rectángulo se corresponde con un circuito cerrado, y la suma de las longitudes de los lados de los cuadrados a izquierda y derecha del segmento valen lo mismo, la longitud del segmento vertical.
La corriente que entra en el circuito eléctrico por el polo positivo, que es igual a la que sale por el polo negativo, es la longitud de los lados horizontales del rectángulo. En el ejemplo de arriba, 14 + 18 = 9 + 8 + 15 = 32. Por otra parte, la diferencia de potencial entre los dos polos es igual a la longitud de los lados verticales del rectángulo. De nuevo, en el ejemplo la diferencia de potencial la podemos calcular a través de cualquiera de los recorridos entre el polo positivo y el negativo, 14 + 10 + 9 = 14 + 4 + 7 + 8 = 18 + 15 = 33, entre otros. Por lo tanto, si la corriente que entra por el polo positivo, y sale por el negativo, es igual a la diferencia de potencial, estaríamos ante un circuito eléctrico que se corresponde con la cuadratura del cuadrado.
 Diagrama de Smith asociado a una cuadratura perfecta de un rectángulo
Diagrama de Smith asociado a una cuadratura perfecta de un rectángulo
En conclusión, cada cuadratura de un rectángulo se corresponde con una red eléctrica, lo cual les permitió utilizar los conocimientos de la teoría de redes eléctricas para estudiar el problema de la cuadratura de los rectángulos, y del cuadrado. Por ejemplo, en la imagen anterior tenemos una red eléctrica, os dejo como divertimento el construir la cuadratura del rectángulo asociada (solución al final de la entrada).
En particular, esto simplificó el problema de construir y clasificar las cuadraturas perfectas simples de rectángulos. Por ejemplo, analizaron todos los circuitos eléctricos con hasta 11 aristas y construyeron las cuadraturas de rectángulos asociadas. Así probaron que no existen cuadraturas perfectas simples de rectángulos de orden menor que 9, que solo hay dos de orden 9 (mostradas en la anterior entrada La cuadratura del cuadrado: en busca del santo grial, una de ellas es la asociada al primer circuito eléctrico que hemos mostrado más arriba), seis de orden 10 y veintidós de orden 11. Y siguieron clasificando las cuadraturas de orden 12, que hay sesenta y siete, y después de orden 13. Este fue el inicio de una fructífera investigación sobre las cuadraturas perfectas de rectángulos. Pero como veremos, también del cuadrado.
Uno de los estudios que realizaron fue el análisis de redes eléctricas con ciertas simetrías. Por ejemplo, consideraron el circuito eléctrico asociado a un cubo, vértices y aristas, que no proporcionaba cuadraturas perfectas de rectángulos, pero cuando se añadía una de las diagonales de una de las caras del cubo, se obtenía el diagrama de Smith de la siguiente imagen y la correspondiente cuadratura perfecta simple del rectángulo, que se muestra después.
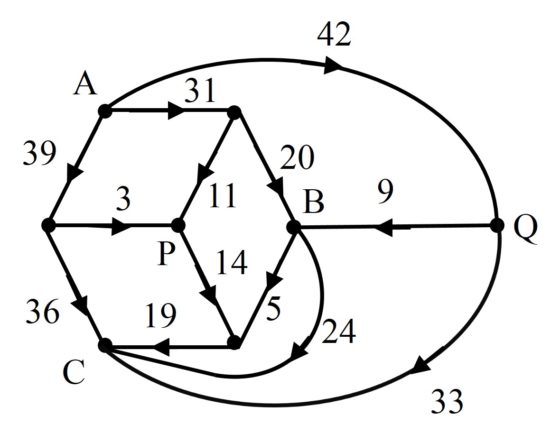 Red eléctrica definida sobre un cubo, junto con una diagonal de una de sus caras, introducida por Brooks, Smith, Stone y Tutte, para construir cuadraturas perfectas simples de rectángulos
Red eléctrica definida sobre un cubo, junto con una diagonal de una de sus caras, introducida por Brooks, Smith, Stone y Tutte, para construir cuadraturas perfectas simples de rectángulos
 Cuadratura perfecta simple de un rectángulo de dimensiones 112 x 75 obtenida a través del circuito eléctrico anterior
Cuadratura perfecta simple de un rectángulo de dimensiones 112 x 75 obtenida a través del circuito eléctrico anterior
Una bonita historia relacionada con esta cuadratura del rectángulo es la siguiente. Leonhard Brooks estaba tan satisfecho con este ejemplo que decidió construirse un rompecabezas geométrico cuyas piezas eran los cuadrados de la cuadratura del rectángulo anterior, es decir, de lados 3, 5, 9, 11, 14, 19, 20, 24, 31, 33, 36, 39 y 42, con el que jugar a realizar el rectángulo original. Entonces su madre cogió el rompecabezas para jugar con él y consiguió formar el rectángulo con ellas, pero resultó que no era la misma solución anterior, las piezas estaban colocadas de forma diferente. Con la ayuda de la madre de Brooks, habían encontrado dos disecciones perfectas simples del rectángulo 112 x 75 realizadas con los mismos cuadrados.
 Segunda cuadratura perfecta simple del rectángulo de dimensiones 112 x 75 realizada con los mismos cuadrados que la anterior
Segunda cuadratura perfecta simple del rectángulo de dimensiones 112 x 75 realizada con los mismos cuadrados que la anterior
La red eléctrica asociada a esta nueva descomposición perfecta y simple del rectángulo 112 x 75 se puede obtener a partir del primer circuito eléctrico (que está representado arriba) identificando los vértices P y Q, lo cual es posible ya que tienen la misma diferencia de potencial, en concreto, 42.
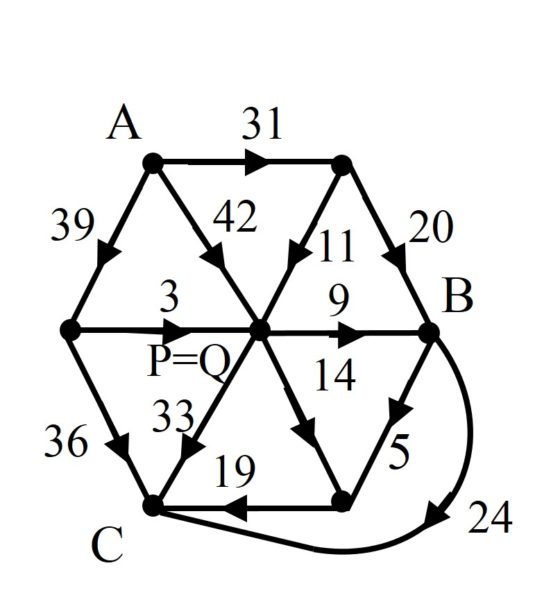 Red eléctrica asociada a la anterior descomposición perfecta simple del rectángulo 112 x 75, que se puede obtener a partir de la anterior identificando P y Q
Red eléctrica asociada a la anterior descomposición perfecta simple del rectángulo 112 x 75, que se puede obtener a partir de la anterior identificando P y Q
Analizaron el motivo por el cual se producía este fenómeno y tenía que ver con la simetría de algunas redes eléctricas, aunque no entraremos en los detalles técnicos en esta entrada, por este motivo empezaron a analizar circuitos eléctricos en los cuales cogían la red eléctrica anterior, que habían obtenido a partir del cubo, y sustituyeron la parte simétrica central (el hexágono plano que contiene a los vértices A, B, C y centro P) por otras estructuras simétricas. Así consiguieron obtener más ejemplos de dobles cuadraturas perfectas simples de un mismo rectángulo con los mismos cuadrados.
Esta técnica, después de seguir investigando y obtener otros ejemplos, les llevó a encontrar su primer ejemplo de cuadratura perfecta de un cuadrado. La pieza central simétrica tenía la siguiente forma.
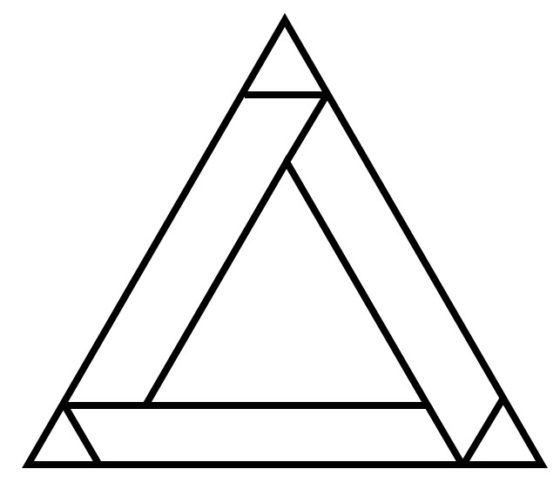
La cuadratura perfecta, que era compuesta, que obtuvieron era de orden 39, es decir, formada por 39 cuadrados de diferentes tamaños, que componían un cuadrado de lado 4.639. Utilizando el código de Bouwkamp que explicamos en la anterior entrada, esta era la cuadratura [2.378, 1.163, 1.098], [65, 1.033], [737, 491], [249, 242], [7, 235], [478, 259], [256], [324, 944], [219, 296], [1.030, 829, 519, 697], [620], [341, 178], [163, 712, 1.564], [201, 440, 157, 31], [126, 409], [283], [1231], [992, 140], [852]. Como cada corchete del código de Bouwkamp nos dice qué cuadrados, su lado, están debajo de cada segmento horizontal, de arriba abajo, podemos ver qué cuadratura prefecta del cuadrado, de lado 4.639, habían construido.
 Cuadratura perfecta, compuesta, de un cuadrado de lado 4.639, de orden 39, construida por Brooks, Smith, Stone y Tutte utilizando la teoría de las redes eléctricas
Cuadratura perfecta, compuesta, de un cuadrado de lado 4.639, de orden 39, construida por Brooks, Smith, Stone y Tutte utilizando la teoría de las redes eléctricas
Poco después, encontrarían el primer ejemplo de cuadratura perfecta simple de un cuadrado de orden 55, utilizando las mismas técnicas.
Como hemos podido ver, relacionar las cuadraturas perfectas de los rectángulos con redes eléctricas se demostró una técnica muy fructífera en la resolución del problema de la cuadratura del cuadrado, y del rectángulo, y en el estudio general de estas cuestiones.
Y, por cierto, la solución a la cuestión planteada arriba sobre cuál es la cuadratura perfecta asociada a la red eléctrica que habíamos mostrado, es la siguiente.
 Cuadratura perfecta simple de un rectángulo de tamaño 106 x 99 de orden 12, que es la solución al divertimento que os he dejado arriba de encontrar la cuadratura asociada a la red eléctrica mostrada
Cuadratura perfecta simple de un rectángulo de tamaño 106 x 99 de orden 12, que es la solución al divertimento que os he dejado arriba de encontrar la cuadratura asociada a la red eléctrica mostrada
Bibliografía
1.- Wolfram MathWorld: Perfect Square Dissection.
2.- Stuart Anderson, Tiling by squares.
3.- Martin Gardner, The 2nd Scientific American Book of Mathematical Puzzles and Diversions, University of Chicago Press, 1987. Contiene el capítulo de W. Th. Tutte Squaring the square.
4.- Wikipedia: Kirchhoff’s circuit laws
5.- Arkadiusz Maciuk, Antoni Smoluk, Tiling by squares, Kirchhoff’s Laws and a Flow Problem in the Economy, Didactics of Mathematics, n. 14 (18), 2017.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo La cuadratura del cuadrado: las redes eléctricas de Kirchhoff se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La cuadratura del cuadrado: en busca del santo grial
- Blanche Descartes y la cuadratura del cuadrado
- ¿Sueñan los babilonios con multiplicaciones eléctricas?
Sólidos cuánticos
 Foto: Pixabay
Foto: PixabayUno de los primeros grandes éxitos de la hipótesis cuántica de Planck surgió, no del estudio de la radiación, sino de la teoría de los sólidos. Una vez más, Albert Einstein fue la vanguardia.
Después de presentar la hipótesis de los cuantos de luz que explicaba el efecto fotoeléctrico en 1905, Einstein demostró en 1906 que los resultados anteriores de Planck sobre la distribución de energía en la radiación electromagnética podrían derivarse utilizando dos supuestos. El primero, ya presente en su artículo de 1905, fue que la luz se compone de cuantos de luz; el segundo fue que los cuantos de luz son emitidos y absorbidos por cargas oscilantes dentro de la materia que vibran solo con ciertas energías cuantificadas. Esto significa que la luz es emitida por cargas oscilantes dentro de la materia, como podría esperarse de la teoría de Maxwell, pero las energías tanto de la luz emitida como de los osciladores están restringidas a ciertos valores permitidos, lo que contradice la teoría clásica. Los osciladores se comportaron como cargas unidas a resortes, oscilando de un lado a otro solo con ciertas frecuencias correspondientes a ciertas energías cuánticas.
En 1904, Paul Drude había propuesto un modelo de sólido cristalino en el que los átomos están dispuestos en una red tridimensional de tal manera que cada átomo está unido a sus átomos vecinos por enlaces que pueden actuar como pequeños muelles (osciladores). Drude demostró, utilizando la física clásica, que la oscilación tridimensional de los átomos de la red puede explicar la absorción observada de la radiación infrarroja por algunos sólidos, si se supone que los átomos están ionizados. Una oscilación similar de los electrones, unidos a los átomos o iones, explicaba la absorción observada de la radiación ultravioleta en estos sólidos.
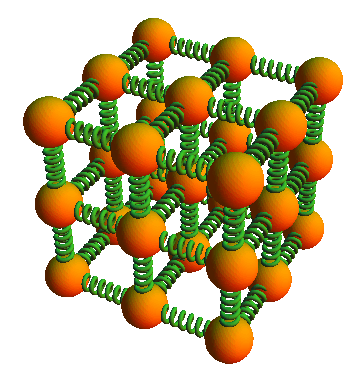 Figura 1. Modelo de Drude de átomos y muelles. Fuente: Wikimedia Commons
Figura 1. Modelo de Drude de átomos y muelles. Fuente: Wikimedia CommonsEn 1907, Einstein aplicó la hipótesis cuántica a los osciladores clásicos de Drude. Incluso antes del modelo de Drude, Einstein había especulado desde 1901 con la idea de que la energía cinética interna de los sólidos y líquidos podría considerarse como la energía de los «resonadores eléctricos». Un enigma considerable en ese momento era el comportamiento del calor específico, c, de los sólidos a medida que la temperatura disminuía. Normalmente se supone que el calor específico es una constante en la relación entre la transferencia de calor y el cambio de temperatura de una sustancia ΔQ = m·c·ΔT [2]. Y la aplicación de la física clásica al modelo de red de átomos y muelles de Drude llega a la conclusión de que, efectivamente, el calor específico c debe ser una constante para los sólidos a todas las temperaturas.
Sin embargo, cuando Einstein aplicó la hipótesis cuántica a los osciladores en el modelo de Drude obtuvo una expresión para el calor específico que afirmaba que el valor del calor específico debería cambiar con la temperatura. Para ser precisos, decía que debería ser constante a temperatura ambiente o algo menos, pero que el calor específico debería caer rápidamente a cero conforme la temperatura se va a cero (absoluto), como se muestra en la figura 2. Visto de otra forma: partiendo desde 0 K, el valor de Einstein para el calor específico de una sustancia cristalina en función de su temperatura debe acercarse a un valor constante que se alcanza más o menos a temperatura ambiente.
 Figura 2. Gráfica original del artículo de Einstein de 1907
Figura 2. Gráfica original del artículo de Einstein de 1907Es importante recalcar esto: las predicciones de Einstein para el comportamiento del calor específico de los sólidos en función de la temperatura se basaron en una aplicación de la hipótesis cuántica a un modelo de un sólido cristalino en el que los átomos de la red se comportan como osciladores tridimensionales que vibran con energías cuantificadas. Los físicos Walther Nernst y Frederick A. Lindemann, que trabajan en un laboratorio de bajas temperaturas en Berlín, asombraron a la comunidad científica con una confirmación completa de la predicción de Einstein sobre la forma en la que el calor específico de un sólido cristalino cambia con la temperatura. Fue la primera confirmación de la hipótesis cuántica fuera del campo de radiación, y demostraba inequívocamente que los sólidos cristalinos pueden considerarse como una red tridimensional de átomos oscilantes sujetos a los requisitos de la hipótesis cuántica y, más tarde, de la mecánica cuántica.
Este modelo ha servido como modelo básico de sólido cristalino desde entonces. Como escribieron Nernst y Lindemann:
«[…] que las observaciones en su totalidad suponen una confirmación brillante de la teoría cuántica de Planck y Einstein es obvio».
Notas:
[1] Este artículo es una adaptación de nuestro Einstein and quantum solids
[2] Nosotros lo asumimos en El misterio de la temperatura constante, por ejemplo. En el ejemplo que usamos en ese texto es suficientemente cierto.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Sólidos cuánticos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Los experimentos de Joule
- La teoría cinética y la segunda ley de la termodinámica
- La ley del gas ideal a partir del modelo cinético
La ciencia al servicio de la guerra
 Lois Cook-Leurgan examinando la unidad aritmética principal del MANIAC ( Mathematical Analyzer, Numerical Integrator And Computer). El ordenador jugó un papel importante en los cálculos termonucleares que se llevaron a cabo en el Los Alamos Scientific Laboratory de la Universidad de California dentro del Proyecto Manhattan. Klara Dan von Neumann fue la autora de los primeros programas.
Lois Cook-Leurgan examinando la unidad aritmética principal del MANIAC ( Mathematical Analyzer, Numerical Integrator And Computer). El ordenador jugó un papel importante en los cálculos termonucleares que se llevaron a cabo en el Los Alamos Scientific Laboratory de la Universidad de California dentro del Proyecto Manhattan. Klara Dan von Neumann fue la autora de los primeros programas.En las guerras siempre se ha utilizado el conocimiento del que se disponía en la época. Por tanto, la ciencia y la tecnología, en tanto que formas de conocimiento, no han sido ajenas a los conflictos bélicos. Más bien habría que decir que las guerras han incentivado la generación de conocimiento científico y tecnológico, y lo siguen haciendo en la actualidad.
A Arquímedes (s III aec) se le atribuye haber inventado un dispositivo basado en espejos ustorios para concentrar rayos de luz solar y producir suficiente calor como para dar fuego a las naves que transportaban las tropas romanas que pretendían ocupar la ciudad de Siracusa. Aunque en realidad, no sabemos si esa atribución es correcta.
Si nos limitamos al siglo XX y lo que llevamos del XXI, está claro que laboratorios y despachos de científicos han tenido un protagonismo determinante en los conflictos bélicos.
Fritz Haber fue galardonado con el premio Nobel por su descubrimiento del proceso llamado de Haber-Bosch, para la síntesis catalítica de amoniaco a partir de hidrógeno y nitrógeno atmosférico bajo condiciones de alta presión y temperatura. Ese proceso abrió la era de la producción industrial de fertilizantes y, en general, de la industria química. Pues bien, él fue el químico al frente del programa de producción de gases letales que utilizó Alemania en la I Guerra Mundial. F Haber puso sus conocimientos al servicio del esfuerzo bélico alemán por su forma de entender el patriotismo; llegó a decir que «en tiempo de paz, un científico pertenece al mundo, pero en tiempo de guerra pertenece a su país».
No solo él, James Franck, Gustav Hertz y Otto Hahn, futuros premios Nobel, también formaron parte de la unidad de Haber. Y en el bando galo, otro galardonado con el Nobel, Victor Grignard, participó en el esfuerzo francés para producir gases venenosos.
El radar, invención basada en la patente obtenida por Robert Watson-Watt (descendiente de James Watt), fue seguramente determinante del curso que siguió la II Guerra mundial. El invento, de 1935, de Watson-Watt se basaba en el uso de ondas de radio para detectar y alertar de movimientos de objetos invisibles con la vista. En este caso se trató de una invención de carácter defensivo (sirvió, entre otras cosas, para poder anticipar los bombardeos alemanes sobre la población civil británica), pero en lo relativo a su influencia sobre el curso de la guerra, a largo plazo no es posible diferenciar la función defensiva de la ofensiva.
El ejemplo más evidente de contribución científica a la guerra es el proyecto Manhattan, nombre clave con el que se conocía el proyecto que desarrolló Estados Unidos para fabricar la bomba atómica durante la II Guerra Mundial. El objetivo del proyecto era producir la bomba antes de que los nazis lo consiguieran. Lo lograron, como es bien sabido. Y como consecuencia de ello, lanzaron sendas bombas sobre las ciudades japonesas de Hirosima y Nagasaki, provocando de esa forma la rendición del Japón. El proyecto, en su parte científica, fue dirigido por el físico Julius Robert Oppenheimer y de una u otra forma, participaren numerosos científicos e ingenieros. También estos científicos tomaron parte en el proyecto por una causa. Todos ellos quisieron colaborar en la derrota de las potencias del Eje.
En las guerras del siglo XXI los científicos e ingenieros siguen teniendo una función determinante en el perfeccionamiento del armamento clásico y en las innovaciones. Drones, robots, inteligencia artificial, sistemas de telecomunicaciones, invisibilidad a los sistemas de detección son áreas en las que los ejércitos más poderosos del mundo invierten enormes cantidades de recursos. Muchos científicos e ingenieros participan en el desarrollo de nuevas ideas con fines militares.
Tanto Haber como Oppenheimer ejemplifican bien el tipo de dilemas éticos al que se han de enfrentar los científicos que toman parte activa en el desarrollo de armas de gran potencial para segar vidas humanas. Ambos actuaron motivados por su compromiso con el destino de los conflictos bélicos en que se vieron involucrados. Haber por patriotismo y Oppenheimer para frenar el avance del fascismo. Sus casos son especiales porque el resultado de su trabajo científico tuvo como consecuencia la pérdida de miles de vidas humanas, pero en rigor, nada los diferencia de la actuación de otros científicos que han desarrollado y desarrollan su actividad al servicio del ejército de sus países.
Este artículo se publicó originalmente en el blog de Jakiunde. Artículo original.
Sobre los autores: Juan Ignacio Perez Iglesias es Director de la Cátedra de Cultura Científica de la UPV/EHU y Joaquín Sevilla Moroder es Director de Cultura y Divulgación de la UPNA.
El artículo La ciencia al servicio de la guerra se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:El límite entre la vida y la muerte en las neuronas
![]()
Jorge Valero Gómez-Lobo y Amanda Sierra
 La apoptosis de la neurona es un tipo de muerte autoinducida.
La apoptosis de la neurona es un tipo de muerte autoinducida.Kateryna Kon / Shutterstock
“Hasta que la muerte nos separe”. Esa es la fecha de caducidad que tienen la mayoría de nuestras neuronas. Estas células, encargadas de transmitir el impulso nervioso en el cerebro, son de las más longevas de nuestro organismo. Nacen prácticamente a la vez que nosotros y, por lo general, no se renuevan.
Pero existe una excepción a toda regla, y esta no iba a ser menos. No hace mucho que sabemos que en el cerebro de la mayoría de los mamíferos se producen nuevas neuronas a lo largo de toda la vida. Este fenómeno, que conocemos como neurogénesis adulta, sólo ocurre en unas pocas regiones del cerebro. Entre ellas el hipocampo, una región especializada en procesos de memoria y aprendizaje.
Las conexiones que establecen las neuronas dan forma a nuestros pensamientos y manera de ser, haciéndolas únicas e insustituibles. De ahí que la pérdida de neuronas que sufrimos al envejecer, o cuando caemos en las garras de una enfermedad neurodegenerativa, suela ser irreparable.
Lo normal es morir
Las neuronas mueren cuando envejecemos debido a que acumulan residuos y defectos que hacen que pierdan su función y degeneren. Este proceso natural se limita a unas pocas neuronas pero se ve agravado en enfermedades neurodegenerativas como las enfermedades de Parkinson o Alzheimer. Sin embargo, también hay mucha muerte neuronal al inicio de la vida.
De hecho, antes del nacimiento se producen muchas más neuronas de las necesarias. Tantas que la mayoría no sobreviven al no establecer las conexiones adecuadas. No solo eso, sino que gran parte de las neuronas que se generan en la vida adulta y sus precursores mueren sin llegar a incorporarse a los circuitos cerebrales. Esta muerte temprana no es patológica: todo lo contrario. Estos procesos de muerte neuronal se producen de forma normal y están destinados a mantener el buen funcionamiento del cerebro.
Una muerte limpia
La muerte temprana de las neuronas se produce de manera controlada a través de un proceso que llamamos apoptosis. Para entendernos, la apoptosis es una tipo de muerte autoinducida y limpia, que no genera desechos tóxicos dispersos y evita daños mayores. Solo deja atrás un residuo: los restos de las células que acaban de morir. Estos “cadáveres neuronales” son eliminados por unas células del cerebro llamadas microglía.
 Microglía (cian) fagocitando una célula muerta, apoptótica. Arriba a la derecha una imagen de los núcleos celulares. La flecha morada señala a la célula muerta, apoptótica. La célula apoptótica tiene un tamaño menor que el resto de núcleos debido a que su contenido se ha compactado. En la imagen inferior derecha se ve la microglía, la flecha blanca señala la prolongación que la microglía extiende hasta la célula muerta.
Microglía (cian) fagocitando una célula muerta, apoptótica. Arriba a la derecha una imagen de los núcleos celulares. La flecha morada señala a la célula muerta, apoptótica. La célula apoptótica tiene un tamaño menor que el resto de núcleos debido a que su contenido se ha compactado. En la imagen inferior derecha se ve la microglía, la flecha blanca señala la prolongación que la microglía extiende hasta la célula muerta.Author provided
Las células de la microglía son células muy dinámicas cuyos cuerpos tiene prolongaciones finas que escanean continuamente el cerebro. Su misión es contener cualquier tipo de daño. Y como parte de esta función se encargan de detectar, englobar y destruir los restos de células muertas.
A este proceso por el que la microglía “se come” a las células muertas y “las digiere” lo llamamos fagocitosis. La fagocitosis es necesaria para evitar que los restos celulares degeneren y produzcan residuos tóxicos. La fagocitosis, por tanto, constituye el último paso en la gestión de la muerte de las neuronas: su eliminación definitiva. Pero, ¿qué ocurre después de la fagocitosis? ¿Acaba ahí, con la eliminación de los residuos?
Microglía en movimiento. Imagen “en vivo” del cultivo de una rodaja de hipocampo. El punto rojo representa la zona en la que se generó daño con un láser.La microglía regula la producción de nuevas neuronas
Los resultados de nuestra investigación muestran que la microglía no se limita a retirar los residuos del sistema sin más. Por el contrario, cuando la microglía se “come” a las células muertas comienza un proceso de auto-reprogramación que cambia la expresión de sus genes. Este cambio en la expresión génica se da, entre otros, en genes que codifican para sustancias que pueden regular la propia neurogénesis. Es decir, que las células de microglía fagocítica liberan factores que limitan la formación de nuevas neuronas. Pero, ¿cuál puede ser el sentido de todo esto?
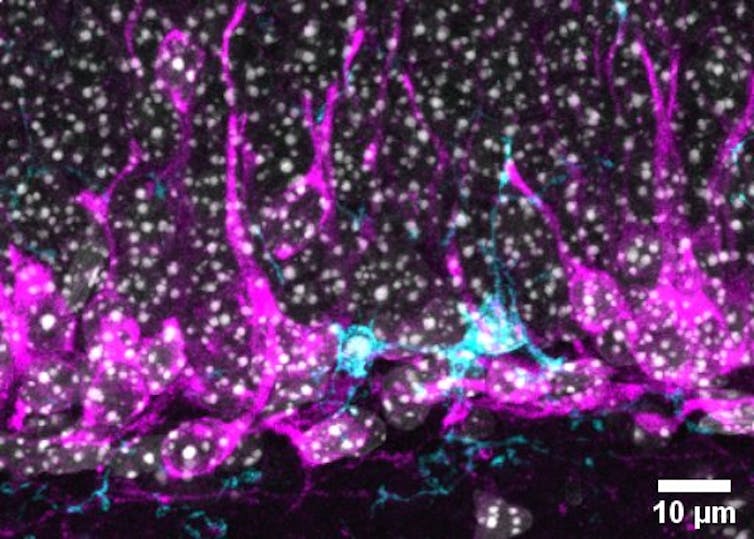 Microglía (cian) fagocitando una célula muerta y rodeada de nuevas neuronas (magenta).
Microglía (cian) fagocitando una célula muerta y rodeada de nuevas neuronas (magenta).Author provided
La formación de nuevas neuronas en el cerebro adulto tiene un coste. Estas neuronas se generan a partir de células madre que se activan y se agotan en el proceso. Producir un exceso de nuevas neuronas cuando no son necesarias agotaría la reserva de células madre rápidamente y la capacidad de formar neuronas cuando realmente se necesite.
La microglía detecta un exceso en la producción de neuronas al fagocitar a aquellas que mueren y, mediante las moléculas que secreta, le indica al hipocampo que frene la producción porque está gastando recursos sin sentido. De esta manera, podemos especular que la microglía fagocítica regula el equilibrio entre la oferta y la demanda, y ajusta la tasa de producción de nuevas neuronas en función de cuántas se mueren y cuántas se pueden incorporar al circuito neuronal.
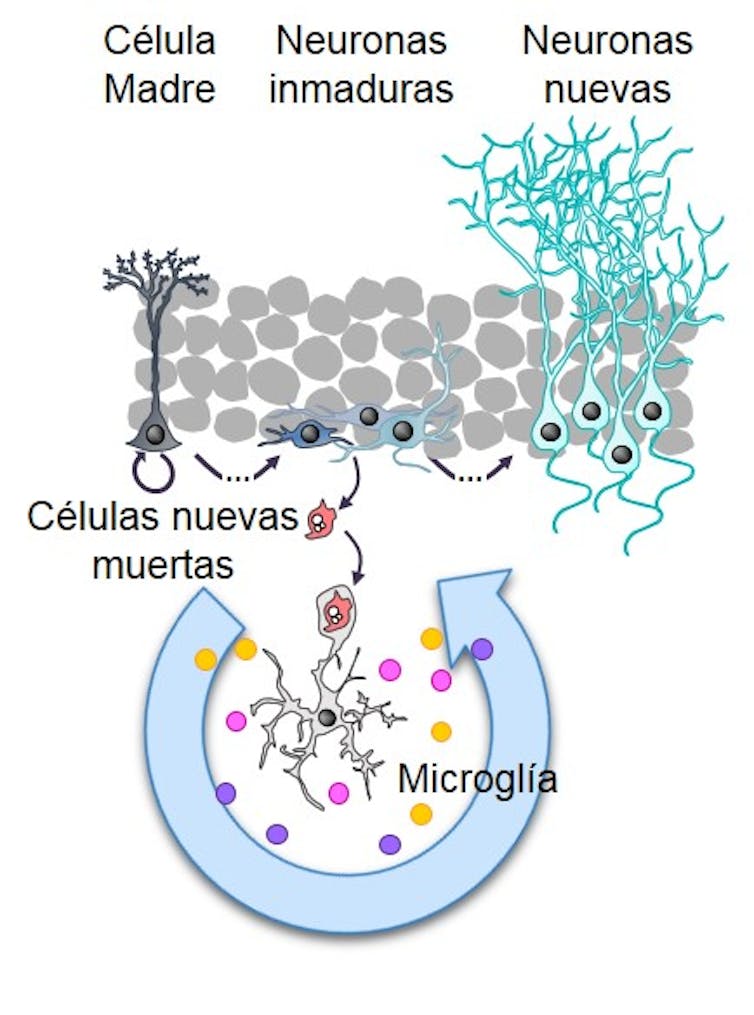 La microglía tras fagocitar libera sustancias que regulan la producción de nuevas neuronas.
La microglía tras fagocitar libera sustancias que regulan la producción de nuevas neuronas.Author provided
Estos hallazgos tienen implicaciones en el campo de las enfermedades neurodegenerativas. En estas patologías, las neuronas mueren y la microglía es la encargada de retirarlas del tejido cerebral. En ocasiones, como hemos observado en anteriores estudios sobre la epilepsia, la naturaleza de la enfermedad impide a la microglía ejercer su función fagocítica y retirar los residuos celulares. Estos resultados nos llevan a plantear lo siguiente: incrementar la actividad fagocítica de la microglía
puede constituir una nueva vía terapéutica.
En los próximos años determinaremos si potenciar los mecanismos de auto-reparación devuelve al cerebro el adecuado equilibrio entre la vida y la muerte en las enfermedades neurodegenerativas.![]()
Sobre los autores: Jorge Valero Gómez-Lobo y Amanda Sierra son investigadores del Achúcarro Basque Center for Neuroscience
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo El límite entre la vida y la muerte en las neuronas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Más allá de las neuronas
- La microglía es un sensor de mortalidad neuronal
- Muerte entre las ecuaciones (Historias de muerte y matemáticas 1)
Las mareas del pasado leídas en las rocas del presente
Los fósiles, los minerales o las rocas son, entre otras cosas, en lo primero que pensamos al hablar de geología, pero lo cierto es que la física es un ámbito científico que difícilmente se puede desvincular de la geología. Y es que el fundamento físico resulta clave a la hora de explicar algunos procesos geológicos que suceden tanto en el océano como en la superficie terrestre.
Con el fin de poner sobre la mesa la estrecha relación entre la geología y la física, los días 27 y 28 de noviembre de 2019 se celebró la jornada divulgativa “Geología para poetas, miopes y despistados: La Geología también tiene su Física”. El evento tuvo lugar en la Sala Baroja del Bizkaia Aretoa de la UPV/EHU en Bilbao.
La segunda edición de esta iniciativa estuvo organizada por miembros del grupo de investigación de Procesos Hidro-Ambientales (HGI) de la Facultad de Ciencia y Tecnología de la Universidad del País Vasco, en colaboración con el Vicerrectorado del Campus de Bizkaia, el Geoparque de la Costa Vasca y la Cátedra de Cultura Científica de la UPV/EHU.

Las mareas, esos movimientos de mares y océanos provocados por la Luna, dejan su marca en el proceso de formación de las rocas sedimentarias. Estas marcas las podemos leer hoy para saber que ocurrió hace millones de años. Lo explica en esta conferencia Isabel Emma Quijada, profesora del departamento de geología de la Universidad de Oviedo.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Las mareas del pasado leídas en las rocas del presente se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La eternidad en un grano de arena
- Geotermia urbana
- Los ecos del fondo submarino: imágenes de las estructuras geológicas.
Estimación de la edad en obras de arte contemporáneas
 Obra de Jesús Mari Lazkano empleada en la investigación. Fuente: UPV/EHU
Obra de Jesús Mari Lazkano empleada en la investigación. Fuente: UPV/EHUEl comercio ilícito de arte se ha convertido en el tercer mercado ilegal a escala mundial después de las drogas y las armas. Una investigación de la UPV/EHU ha desarrollado un novedoso método para la datación de obras de arte contemporáneo, hasta la fecha no existía ninguno, a través del estudio del proceso de envejecimiento de las pinturas acrílicas.
El objetivo era conseguir una correcta identificación y datación precisa de los materiales utilizados en las obras que pudiese ayudar en la detección de trabajos falsificados o mal atribuidos. “El punto de partida del estudio es conocer cómo envejecen las pinturas acrílicas en el arte contemporáneo, y determinar que llevan depositadas el mismo tiempo que el que se supone que tiene la obra, para poder así decir si esa obra tiene 20 años por ejemplo o está hecha antes de ayer”, cuenta Itxaso Maguregi, profesora de Bellas Artes y coautora del trabajo.
“El principal problema del arte contemporáneos es que los materiales utilizados para las obras se pueden encontrar a día de hoy fácilmente, por tanto, las falsificaciones son más sencillas, de ahí la importancia de este estudio”, explica Luis Bartolomé, otro de los coautores.
Para ello, las pinturas fueron sometidas a ensayos de envejecimiento acelerado, mediante el uso de cámaras con condiciones de luz, temperatura y humedad controladas que permiten recrear el paso del tiempo en las pinturas. “50 horas en la cámara equivaldría a un año de envejecimiento natural, y se monitorizó su evolución química a fin de desarrollar modelos matemáticos de predicción de edad. Básicamente lo que se ha realizado ha sido un estudio controlado del envejecimiento de una pintura acrílica, mediante un time lapse de la pintura”, señala Luis Bartolomé.
Tras la realización del ‘envejecimiento artificial’ se logra una serie de patrones, de muestras, que sirven para comparar con la obra original. “Una vez que creamos nuestra ‘serie patrón de muestras artificiales’, incorporamos muestras reales para compararlas. Así, hemos visto que nuestro modelo funcionaba correctamente porque estimaba justamente la edad que tenían las obras reales. Por ejemplo, se pudo ratificar que un cuadro cedido por el pintor vasco Jesús Mari Lazkano y realizado en el año 2015 tenía 4 años de antigüedad”, asegura Bartolomé.
Esta correlación ha podido utilizarse para fechar obras de hasta 22 años, conservadas en condiciones comparables y creadas con el mismo tipo de pintura. “Esta metodología podría ser un primer paso para fechar obras pictóricas contemporáneas. Asimismo, este trabajo puede resultar de ayuda en el desarrollo de otras metodologías apropiadas de conservación y restauración en pintura contemporánea”, exponen las investigadoras Laura Ortiz-Herrero e Irene Cardaba.
Referencia:
L.Ortiz-Herrero, I.Cardaba, S.Setien, L.Bartolomé, M.L.Alonso, M.I.Maguregui (2019) OPLS multivariate regression of FTIR-ATR spectra of acrylic paints for age estimation in contemporary artworks Talanta doi: 10.1016/j.talanta.2019.120114
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo Estimación de la edad en obras de arte contemporáneas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Arte & Ciencia: Cómo descubrir secretos que esconden las obras de arte
- Arte & Ciencia: Conservación de obras con componentes tecnológicos
- Técnicas «low cost» para el estudio de obras de arte

