El problema del final feliz
Casi todos los domingos del invierno de 1933, un pequeño grupo de estudiantes se reunía en algún lugar (un parque o un café) de Budapest para hablar de matemáticas. El especial grupo al que me refiero estaba formado, entre otras personas, por Paul Erdős (1913-1996), Esther Klein (1910-2005), Márta Svéd (¿1910?-2005), George Szekeres (1911-2005) y Pál Turán (1910-1976).
 En esta imagen aparecen tres de los protagonistas citados arriba, pero con algunos años más. De izquierda a derecha: Carole Lacampagne, Roger Eggleton, Esther Szekeres (Klein de nacimiento), Paul Erdös, George Szekeres y John Selfridge en 1984.
En esta imagen aparecen tres de los protagonistas citados arriba, pero con algunos años más. De izquierda a derecha: Carole Lacampagne, Roger Eggleton, Esther Szekeres (Klein de nacimiento), Paul Erdös, George Szekeres y John Selfridge en 1984.©The University of Newcastle; UON Photographer.
En una de estas reuniones, Esther propuso el siguiente problema:
Dados cinco puntos en el plano en posición general, demostrar que cuatro de ellos forman un cuadrilátero convexo.
Tras dejar al resto del grupo un tiempo para reflexionar sobre el problema, Esther explicó a sus colegas la demostración que ella había pensado.
En 1935 Erdős y Szekeres publicaron un artículo en el que se generalizaba el resultado de Esther (ver [1]); es uno de los trabajos fundamentales de la geometría combinatoria. Paul Erdős denominó el problema original como “El problema del final feliz” porque Esther y George se casaron en 1937… ¿tras conocerse mejor gracias a este enunciado?
Empecemos por aclarar los conceptos involucrados en la proposición de Esther. Que varios puntos del plano estén en posición general significa que no existe ningún subconjunto formado por tres de ellos que sean colineales. Un cuadrilátero es convexo si todos sus ángulos interiores son menores que 180 grados.
La solución de Esther se basaba en que existen tres formas diferentes en las que un polígono convexo encierra cinco puntos. Dicho de otra manera, dados cinco puntos en posición general, su envolvente convexa puede ser uno de los tres polígonos siguientes:
-
puede ser un cuadrilátero cuyos vértices son cuatro de los puntos del conjunto inicial y que deja en su interior el punto restante. En este caso, la solución ya es inmediata;
-
la envolvente convexa puede ser un pentágono cuyos vértices son los cinco puntos dados. Entonces cuatro de esos puntos pueden conectarse para formar un cuadrilátero convexo;
-
finalmente, si la envolvente es un triángulo, los dos puntos que quedan dentro de la figura definen una recta que divide el triángulo en dos partes. En una de ellas hay dos puntos y en la otra uno de los del conjunto de cinco puntos inicial. Estos dos puntos y los interiores forman automáticamente un cuadrilátero convexo.
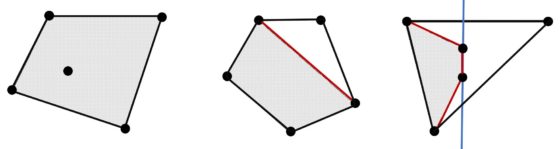 Los tres casos posibles de envolventes convexas y los cuadriláteros convexos obtenidos.
Los tres casos posibles de envolventes convexas y los cuadriláteros convexos obtenidos.
Como hemos comentado antes, Erdős y Szekeres publicaron en 1935 (ver [1]) una generalización del problema planteado por Esther Klein. El artículo comenzaba del siguiente modo:
El problema que nos ocupa ha sido sugerido por la señorita Esther Klein en relación con la siguiente proposición.
A partir de cinco puntos del plano de los cuales no hay tres en una misma línea recta, siempre es posible seleccionar cuatro puntos que determinan un cuadrilátero convexo.
[…] La señorita Klein sugirió el siguiente problema más general. Dado un entero positivo n, ¿es posible encontrar un número N(n) tal que de cualquier conjunto que contenga al menos N(n) puntos sea posible seleccionar n puntos que formen un polígono convexo?
Hay dos preguntas particulares: (1) ¿existe el número N(n) correspondiente a n? (2) Si es así, ¿cómo se determina el menor N(n) en función de n? (denotamos el menor N por N0(n)).
 Principio del artículo [1]
Principio del artículo [1]
En [1] los autores demostraban que el número N(n) existe (para n mayor que 2) y conjeturaban que
![]()
basándose en algún caso particular demostrado por otros autores. De hecho, es obvio que N0(3)=3, Esther Klein demostró que N0(4)=5 y en [1] se afirma que E Makai probó que N0(5)=9, aunque no existe evidencia escrita de ello. Años más tarde Szekeres y Lindsay Peters (ver [2]) demostraron con ayuda de un ordenador que N0(6)=17, reafirmando la conjetura.
Y, de momento nadie ha sido capaz de confirmar o refutar la conjetura. Pero la propuesta se ha reformulado proponiendo la alternativa siguiente (ver, por ejemplo, [4]):
![]()
donde la O mayúscula se refiere a la notación de Landau. Confiemos en que pronto se conocerá más sobre esta interesante acotación.
Por cierto, la historia de amor (el “final feliz” entre sus dos colegas, como lo denominaría Erdös) de Esther y George fue larga e incluso poética en su despedida: ambos fallecieron el 28 de agosto de 2005, con una hora de diferencia. Ella tenía 95 años, él 94… y ambos número de Erdös igual a 1.
Referencias
[1] Paul Erdös and George Szekeres, A combinatorial problem in geometry, Compositio Math. 2 (1935), 463-470.
[2] George Szekeres and Lindsay Peters, Computer solution to the 17-point Erdös-Szekeres problem, ANZIAM J. 48 (2006), 151-164
[3] Pierre-Alain Cherix, Shaula Fiorelli Vilmart, Pierre de la harpe, Polygones convexes : le problème de la fin heureuse, Images des Mathématiques, CNRS, 2014
[4] Sara Freyland, The Happy Ending Problem and its connection to Ramsey theory, Report Uppsala University, 2019
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo El problema del final feliz se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El problema de la plantación de árboles en filas (2)
- Un dulce problema de Paul Erdös
- El problema de la plantación de árboles en filas
Superconductores
 El Shanghai Transrapid une el aeropuerto Shanghai Pudong con la estación de Longyang. Es un maglev comercial que alcanza los 431 km/h de velocidad de crucero. Fuente: Wikimedia Commons
El Shanghai Transrapid une el aeropuerto Shanghai Pudong con la estación de Longyang. Es un maglev comercial que alcanza los 431 km/h de velocidad de crucero. Fuente: Wikimedia CommonsLa teoría de la bandas ha sido sometida a pruebas experimentales muchas veces y ahora es el modelo de consenso para el comportamiento de conductores y aislantes. Pero tenemos que modificarla para poder explicar la superconductividad.
El modelo de Drude-Lorentz introdujo la idea de que la resistencia eléctrica se debe a colisiones de los electrones [1] con impurezas, imperfecciones y especialmente con las vibraciones reticulares del cristal. Las vibraciones reticulares del sólido disminuirán a medida que disminuya la temperatura, porque la entropía, que representa el desorden [2], también disminuye. Por lo tanto, la resistencia también debería disminuir. Esto es lo que se observa, y está bien explicado por la teoría cuántica de bandas. Pero a temperaturas muy bajas sucede algo extraño: la resistencia de algunos materiales cae repentinamente a cero a partir de cierta temperatura.
Estos materiales se convierten en superconductores, lo que significa que pueden conducir corrientes sin resistencia o, lo que es equivalente, sin pérdida de energía. La temperatura a partir de la que se produce la superconductividad se denomina temperatura crítica. Varía desde 0.015 K para el tungsteno [3], 160 K para ciertas cerámicas, hasta 250 K para algunas formas cristalinas de superhidruro de lantano [4][5].
Podemos imaginar algunas de las posibles ventajas de unos cables eléctricos con resistencia cero. Es como un movimiento sin fricción. Entre las muchas aplicaciones reales y potenciales están las líneas de transmisión eléctrica sin pérdida de energía, ordenadores más rápidas y electroimanes con una fuerza colosal. Estos últimos se usan actualmente en dispositivos de resonancia magnética (MRI), aceleradores de partículas de alta energía y trenes de levitación de alta velocidad, a menudo llamados «mag-lev» [6]. Dado que la temperatura de ebullición del nitrógeno líquido, que es abundante y relativamente fácil de producir, es de 77 K, los superconductores con temperaturas críticas superiores a 77 K pueden mantenerse lo suficientemente fríos manteniéndolos sumergidos en nitrógeno líquido. Sin embargo, un gran inconveniente de estos materiales es que son frágiles, no porque se puedan romper con facilidad, sino porque la superconductividad puede destruirse fácilmente por un campo magnético que no esté controlado. Como es lógico, se investiga intensamente para superar estos problemas y crear materiales superconductores con temperaturas de transición lo más cercanas que sea posible la temperatura ambiente (20 ° C o 293 K) [7].
El desarrollo de dispositivos superconductores tuvo un impulso enorme tras la aparición del modelo básico de la superconductividad propuesto en 1957 por John Bardeen, Leon Cooper y Robert Schrieffer. Los autores de la teoría BCS, como se le conoce, recibieron el Premio Nobel por su trabajo en 1972. Su teoría es altamente técnica, pero la idea básica es que las ondas de electrones en el estado superconductor ya no actúan de forma independiente, como en el modelo de Bloch. En cambio, se emparejan a la temperatura crítica de modo que sus funciones de onda actúan como una unidad a medida que interactúan con la red cristalina. Además, todos los pares de electrones se mueven juntos en un movimiento colectivo, de modo que si un solo electrón se dispersa por la red, su compañero “lo arrastra” hacia la corriente general, y si algún par de electrones se dispersa de alguna manera fuera de la ruta general, todos los demás pares “lo traen” de regreso al flujo colectivo. Como no hay dispersión o colisiones inelásticas, no hay resistencia y el material se convierte en un superconductor.
Aunque la teoría BCS explica bien en general ciertos sólidos cristalinos, se requieren más refinamientos del modelo para otros materiales [8] y para explicar el comportamiento de los superconductores en detalle.
Notas:
[1] Da igual si los tratamos como ondas o como corpúsculos.
[2] En puridad esto es una afirmación muy grosera, pero tolérese para poder visualizar lo que ocurre.
[3] En esta casa obedecemos las normas IUPAC.
[4] En concreto una forma del LaH10 altamente simétrica (grupo espacial Fm-3m), en la que una jaula de hidrógeno envuelve los átomos de lantano. Véase.
[5] Récord a la fecha de publicación. Cualquiera sabe cuando estés leyendo esto.
[6] De levitación magnética dicho en inglés.
[7] 20ºC es la temperatura ambiente estándar. Si nos fijamos ya se ha conseguido la superconductividad a temperatura ambiente en algunas regiones de la superficie del planeta Tierra en según qué épocas del año: 250 K son -23º C.
[8] Véase, por ejemplo, esto.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Superconductores se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Tipos de comportamiento conductor
- La ley del gas ideal y la tercera ley de la termodinámica
- El modelo clásico de electrones libres de Drude-Lorentz
A tomar el sol
 Foto: Mincho Kavaldzhiev / Unsplash
Foto: Mincho Kavaldzhiev / UnsplashEn las últimas décadas los expertos han recomendado evitar las exposiciones excesivas al sol pues son la principal causa de daños en la piel y, sobre todo, de la aparición de melanoma, un cáncer extendido y muy peligroso. La revisión, publicada en 2017, por Natalie Matthew y sus colegas, de la Universidad de Providence, en Estados Unidos, informa de que la incidencia del melanoma en todo el planeta ha crecido con rapidez en los últimos 50 años.
La tasa es mayor en personas de piel blanca y en zonas cercanas a los trópicos y al ecuador. Nuestra especie apareció en los trópicos del centro de África, un área geográfica con mucho sol. Homo necesita sol para el metabolismo de la vitamina D en la piel. Sin embargo, la exposición al sol es peligrosa por los rayos ultravioleta que tiene y, para evitarlos, apareció la melanina, el pigmento que oscurece la piel y evita los ultravioleta. Pero, cuando nuestra especie salió de África hacia el norte, hacia Eurasia, colonizó zonas con menos incidencia solar y, por tanto, menos producción de vitamina D en la piel. Se aclaró la piel y se seleccionó piel blanca, con poca melanina, que dejaba pasar la luz solar y permitía la síntesis de vitamina D. Pero, con el tiempo, los originarios de Eurasia se extendieron por todo el planeta, y, con su piel blanca, muchos volvieron a los trópicos, con demasiado sol para este tipo de piel con escasa melanina protectora. El exceso de sol, con su componente ultravioleta, produce daños en la piel y, en último término, la aparición del melanoma.
En conclusión, la relación de la piel de nuestra especie con el sol es complicada: buena para la vitamina D y dañina por el exceso con desarrollo de cáncer. Hasta ahora se ha intentado evitar el melanoma y, para conseguirlo, los protocolos de exposición al sol piden evitar el exceso y el uso de protectores solares.
Para explicar brevemente los efectos sobre la salud de la deficiencia en vitamina D, nos sirve la revisión publicada por Michael Holick, de la Universidad de Boston, el año pasado. Enumera, como consecuencia de la falta de vitamina D, a enfermedades agudas y crónicas como la caries en niños, osteoporosis, psoriasis, enfermedades autoinmunes, enfermedades cardiovasculares, algunos tipos de cáncer, diabetes tipo 2 y desordenes neurológicos.
Hay que tener mucho cuidado con el sol y, para tomarlo, no hacerlo a las horas centrales del día, cubierta la cabeza, con ropa adecuada y gafas de sol y, siempre, con protector solar, a ser posible con un factor superior a 30.
Pero, hemos visto que la vitamina D es esencial para muchas funciones del organismo y se sintetiza en la piel por la acción de los rayos ultravioleta solares. Eleni Linos y su equipo, de la Universidad de Stanford, aseguran que tanta protección frente al sol puede afectar a los niveles de vitamina D en el organismo. Esta deficiencia vitamínica, como hemos visto, aumenta el riesgo de varias enfermedades y en ello interviene el uso de los protectores solares.
Los protectores solares, en experimentos de laboratorio y en experimentos controlados, reducen los niveles de vitamina D. Ahora Eleni Linos pretende relacionar los niveles de vitamina D con el uso de protectores solares en la población en general y en situaciones de vida normal. A partir de una encuesta nacional sobre salud en Estados Unidos, con datos tomados de 2003 a 2006 a 5920 personas, consigue, por una parte, conocer el uso de protectores solares y, por otra, el nivel de vitamina D en sangre de los voluntarios (en realidad, del precursor 25-hidroxi-vitamina D que pasa a vitamina D en el riñón).
Al analizar los resultados, los autores encuentran que más de la mitad de los encuestados se protegen del sol de alguna manera, aunque el método varía según la raza, sobre todo en relación con los protectores solares: más de la mitad de los blancos (56%) los utilizan con frecuencia mientras que sólo lo hace un tercio de los hispanos (31%) y algo menos de la sexta parte de los negros (14%). Estar a la sombra, en cambio, es más frecuente en hispanos (37%) y negros (43%) que en blancos (25%). En cuanto al nivel de vitamina D en sangre, más del 70% de los que tienen deficiencia se protegen del sol a la sombra o usan la ropa adecuada (sobre todo las camisas de manga larga).
Las conclusiones son curiosas: la deficiencia en vitamina D la provoca la sombra y las mangas largas, no así los protectores solares que, según los investigadores, se utilizan poco o en poca cantidad y, por tanto, no protegen adecuadamente del sol y, de rebote, no provocan niveles bajos de vitamina D.
Hay que añadir que el grupo de Pelle Lindqvist, del Instituto Karolinska de Estocolmo, ha encontrado una relación entre evitar la exposición al sol y la tasa de mortalidad. Ha revisado datos de 29518 mujeres entre 1990 y la actualidad y que tenían de 25 a 64 años cuando se inició el estudio. Para este estudio, tomar poco el sol es, durante el verano, no tomarlo nunca, y tomarlo mucho es, en verano, hacerlo más de 30 veces.
Hasta 2011, fecha de la revisión de datos, habían muerto 2545 voluntarias. El número de fallecimientos es mayor cuanto menos se toma el sol. No hay que olvidar que los datos son de Suecia, un país al norte y con escasez de sol. Cuando se compara la mortalidad entre las que evitan el sol y las que lo toman, la tasa de mortalidad se dobla entre las que lo evitan. Para los autores, la causa está en la deficiencia en vitamina D, con las consecuencias para la salud que antes he mencionado. Conciliar el riesgo de melanoma con la deficiencia en vitamina D necesita un estudio más detallado y preciso para elaborar un protocolo adecuado.
El mismo grupo de Estocolmo estableció poco después que tomar el sol baja la tasa de mortalidad por enfermedades cardiovasculares y por otras enfermedades excepto cáncer. Calculan, por el contrario, que evitar el sol disminuye la esperanza de vida entre 0.6 y 2.1 años. Debido a la mayor esperanza de vida y a que evitan algunas enfermedades, las mujeres que toman el sol padecen cáncer años más tarde.
En conclusión, la radiación solar ultravioleta es esencial para la síntesis de vitamina D pero, a la vez, crece el riesgo de cáncer de piel, del peligroso melanoma. Sin embargo, cuando se ha buscado una relación entre el nivel de vitamina D con el riesgo de melanoma, no s eha encontrado. El estudio de Upekha Liyanage y su grupo, del Instituto de Investigación Médica Berghofer de Brisbane, en Australia, con datos de 36077 voluntarios, concluye que los niveles de vitamina D no se pueden asociar como causa y efecto con el riesgo de melanoma.
 Foto: Dimitris Vetsikas / Pixabay
Foto: Dimitris Vetsikas / PixabayQueda por mencionar un inesperado daño colateral en esta conducta de evitar el sol: la contaminación marina provocada por los protectores solares. Fue un grupo de las islas Baleares el primero en detectarlo en Mallorca.
El riesgo asociado a la exposición al sol ha llevado, en los últimos 80 años y según cuentan Antonio Tovar y sus colegas del Instituto Mediterráneo de Estudios Avanzados de Esporles, en Mallorca, a la invención, desarrollo y producción masiva de protectores solares. En consecuencia, también ha llegado su entrada masiva en el ambiente marino costero.
Su composición es compleja, con sustancias que filtran los rayos ultravioleta, algunas orgánicas como los aminobenzoatos, las benzofenonas, los derivados del alcanfor y muchos más, y otras inorgánicas como los óxidos de titanio o de zinc. Todas ellas reflejan y dispersan la radiación ultravioleta e impiden que llegue a la piel. Hay unos 45 compuestos de este tipo cuya producción está regulada en diferentes países.
Además de estas sustancias que actúan como filtros de ultravioleta, una crema solar lleva conservantes, colorantes, agentes que forman geles sobre la piel, controladores de viscosidad, fragancias, etcétera. Y todos ellos acaban, antes o después, en el ambiente, sobre todo en el mar.
El grupo de Antonio Tovar ha medido la presencia de alguno de estos compuestos en cinco puntos de tres zonas de costa de la isla de Mallorca con gran ocupación (entre 3 y 5 personas por metro de costa), en agosto y septiembre de 2011, temporada alta de turismo.
El análisis de las muestras de agua demuestra que los cuatro productos medidos están en el medio. Hay una benzofenona entre 53.6 y 577.5 nanogramos (millonésima parte del miligramo) por litro; un derivado del alcanfor entre 51.4 y 113.4 nanogramos por litro; óxido de titanio entre 6.9 y 37.6 microgramos (millonésima parte del gramo) por litro; y óxido de zinc entre 1.0 y 3.3 microgramos por litro. Estas concentraciones varían entre puntos de muestreo y, también a lo largo del día con el máximo entre las 14.00 y las 18.00 horas.
Para conseguir una primera aproximación de la posible influencia de estos compuestos en el medio marino, los ensayan sobre el crecimiento de un alga diatomea habitual en la zona, la Chaetoceras gracilis, y en ensayos cortos de 72 horas, en lo que se denomina toxicidad aguda. Con todos los compuestos hay una caída del crecimiento de la diatomea aunque las concentraciones necesarias son mucho más altas, a nivel de miligramos por litro, es decir, un millón de veces más altas que las encontradas en las playas. Pero no hay que olvidar que el periodo de exposición en el experimento era muy corto, solo 72 horas, y a más largo plazo, semanas, meses o años, incluso con concentraciones más bajas, no conocemos los efectos que provocan y los componentes de los protectores solares podrían ser peligrosos.
Referencias:
Holick, M.F. 2017. The vitamin D deficiency pandemic: Approaches for diagnosis, treatment and prevention. Reviews in Endocrine and Metabolic Disorders 18: 153-165.
Lindqvist, P.G. et al. 2014. Avoidance of sun exposure as a risk factor for all-cause mortality: results from the Melanoma in Southern Sweden cohort. Journal of Internal Medicine doi: 10.1111/joim.12251
Lindqvist, P.G. et al. 2016. Avoidance of sun exposure as a risk factor for major causes of death: a competing risk analysis of the Melanoma in Southern Sweden cohort. Journal of Internal Medicine doi: 10.1111/joim.12496
Linos, E. et al. 2012. Sun protective behaviors and vitamina D levels in the US population: NHANES 2003-2006. Cancer Causes Control 23: 133-140.
Liyanage, U.E. et al. 2020. Is there a causal relationship between vitamin D and melanoma risk? A Mendelian randomization study. British Journal of Dermatology 182: 97-103.
Matthews, N.H. et al. 2017. Epidemiology of melanoima. En “Cutaneous melanoma: ethology and therapy”, p. 3-22. Ed. por W.H. Ward & J.M. Farma. Codon Publ. Brisbane, Australia.
Tovar-Sánchez, A. et al. 2013. Sunscreen products as emerging pollutants to coastal waters. PLOS ONE 8: e6545
Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.
El artículo A tomar el sol se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Las mutaciones que aclaran la piel
- Biomarcadores para la detección precoz del melanoma
- Cómo nos ayuda la ciencia a tomar decisiones correctas
La hipótesis de la abuela
 Foto: djmboxsterman / Pixabay
Foto: djmboxsterman / PixabayLa menopausia es, desde una perspectiva evolutiva y en apariencia, una anomalía. De hecho, es un fenómeno muy poco frecuente en el mundo animal. En casi todas las especies las hembras se mantienen fértiles a lo largo de toda su vida. Nuestra especie forma parte de un pequeño grupo de mamíferos en los que la capacidad reproductiva se deteriora de forma acelerada con relación al declive orgánico general. El grupo lo forman, además de la especie humana, el calderón tropical, la beluga, el narval y la orca, todos ellos cetáceos odontocetos. Las hembras de esas especies pueden vivir décadas después de cesar de ovular y, por lo tanto, de poder procrear.
El biólogo norteamericano George C Williams propuso en 1957 que la menopausia podría ser, en realidad, una adaptación. Pensó que desde el punto de vista evolutivo, podría resultar más conveniente para las mujeres dedicar sus esfuerzos a apoyar a sus descendientes que tener ellas una progenie mayor. Conforme envejecemos aumenta la probabilidad de morir, por lo que si una mujer tiene descendencia a una edad avanzada, no sería improbable que sus últimos hijos no pudieran sobrevivir al morir ella. En tal caso, el esfuerzo que esa mujer hubiese dedicado a esos últimos hijos habría resultado baldío, pues sus genes no habrían podido replicarse y ser transmitidos a las siguientes generaciones a través de esos últimos descendientes. Por otro lado, que en una población haya individuos que no se reproducen carece de sentido desde un punto de vista evolutivo, pues esos individuos consumen unos recursos que podrían utilizar otros en beneficio de su propia progenie.
Por estas razones, Williams propuso que las mujeres de mayor edad contribuyen de una forma más efectiva a transmitir sus genes a las generaciones posteriores dedicando sus esfuerzos a los descendientes que ya forman parte del grupo, o sea, a sus nietos y nietas, en vez de hacerlo a los hijos e hijas que a una edad avanzada pudiera llegar a tener ellas mismas.
La “hipótesis de la abuela”, como se conoce en la actualidad la propuesta de Williams, cuenta con respaldo empírico en nuestra especie. Tanto en grupos de cazadores-recolectores, como en sociedades preindustriales se ha comprobado que las abuelas que no se reproducen aumentan la probabilidad de supervivencia de sus nietos. En otras palabras, su presencia en el grupo facilita que sus genes –los que han llegado hasta los nietos- perduren tras su propia muerte o, dicho en lenguaje darwinista, mejore su propia adecuación o éxito evolutivo (fitness) a través del cuidado que presta a sus nietos.
Hay especies, como el elefante asiático y posiblemente también los africanos, de las que sabemos que las abuelas mejoran la supervivencia de los nietos, aunque en este caso las abuelas se siguen reproduciendo. Pero aparte de la especie humana, en ningún otro animal se contaba con pruebas fehacientes en favor de la “hipótesis de la abuela”. Hasta hace unas semanas, pues se acaba de publicar un estudio con orcas –también llamadas, impropiamente, ballenas asesinas- que documenta el efecto positivo de abuelas que no se reproducen en la supervivencia de sus nietos. El estudio recién publicado no solo confirma ese efecto, también muestra que las abuelas que siguen procreando no prestan un apoyo similar al que brindan las orcas menopaúsicas.
La importancia que ese periodo posmenopáusico tan extenso tiene en seres humanos y en orcas habría impulsado, según los especialistas, un aumento en la longevidad de las dos especies, pues la mayor supervivencia de los nietos durante los años de vida añadidos habría compensado con creces, en términos evolutivos, el cese de la procreación.
Fuente: S. Nattrass et al (2019): Postreproductive killer whale grandmothers improve the survival of their grandoffspring. PNAS.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo La hipótesis de la abuela se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Herramientas de luz: de la ciencia ficción a las películas moleculares

Desde su descubrimiento en 1960, los rayos láser han servido de inspiración de películas y series de ciencia ficción. Gracias a desarrollos posteriores algunas de estas fantasías se han hecho realidad. De hecho, ha sido posible crear potentes herramientas de luz de aplicación en ámbitos tan diversos como la biología, la medicina, la industria, las telecomunicaciones o la investigación básica en general.
La conferencia titulada “Herramientas de luz: de la ciencia ficción a las películas moleculares” describe algunas de estas aplicaciones de los rayos láser y abordará las nuevas perspectivas que existen con las fuentes láser de gran intensidad concentrada en pulsos de tiempos muy cortos. Estas fuentes láser permiten filmar los procesos moleculares o incluso adentrarse en el mundo de los electrones, ámbitos antes inexplorables para la ciencia.
Nerea Zabala es la ponente de esta charla del ciclo Bidebarrieta Científica, iniciativa impulsada por la Cátedra de Cultura Científica de la UPV/EHU y la Biblioteca Bidebarrieta. La conferencia ttuvo lugar el pasado 26 de febrero de 2020 en la Biblioteca Bidebarrieta de Bilbao.
Nerea Zabala, doctora en Física, es investigadora asociada en el Centro de Física de Materiales (centro mixto CSIC-UPV/EHU) y en el Donostia International Physics Center (DIPC), y profesora en la Facultad de Ciencia y Tecnología de la UPV/EHU. Actualmente su investigación se centra en el estudio del comportamiento de la luz en la nanoescala.
Edición realizada por César ToméLópez
El artículo Herramientas de luz: de la ciencia ficción a las películas moleculares se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- #NaukasKids14 Física y ciencia ficción
- Un equipo de alta fidelidad de ciencia ficción
- Ciencia, arte y cultura callejera: física y música
Lo que la búsqueda de inteligencia extraterrestre nos enseña para entender la pandemia
 Unsplash/Donald Giannatti, CC BY-SA
Unsplash/Donald Giannatti, CC BY-SAComprender el significado de los números cuando se refieren a cantidades muy grandes o muy pequeñas es complicado. Esto es algo que experimentamos ahora mismo con la pandemia del COVID-19. La combinación de unos números muy grandes (la población total susceptible de ser contagiada) junto con unas probabilidades ínfimas (las asociadas al contagio individual y a la aparición de determinados síntomas graves) da como resultado unas cantidades de muy difícil interpretación. Sobre todo si ignoramos la disponibilidad de servicios hospitalarios. Así, las diferencias entre el riesgo individual y el comunitario se entremezclan y en ocasiones se oscila entre el excesivo alarmismo y el optimismo injustificado.
Para ilustrar esta situación en un contexto más amable, podemos utilizar la fórmula presentada en 1961 por el radioastrónomo Frank Drake para dar una base cuantitativa al proyecto SETI (Search for ExtraTerrestrial Intelligence) en la segunda mitad del siglo XX. SETI suponía un intento científico para determinar la probabilidad de establecer contacto con civilizaciones extraterrestres en nuestra galaxia, algo que muchos verán como mera ciencia-ficción pero que podemos abordar con un espíritu analítico.
¿Cómo podríamos determinar el número de eventos de un determinado suceso tan improbable como la comunicación con una sociedad tecnológica extraterrestre? La estrategia consiste en separar los factores que deben concatenarse para lograr un positivo. Asumiremos que todos estos sucesos son independientes y que, por lo tanto, podemos determinar la probabilidad de que se den simultáneamente con una sencilla multiplicación. Añadiendo factores podemos llegar a una estimación razonable sobre la probabilidad del evento final: aquel en el que todos los sucesos se combinan perfectamente.
Esta tarea abarca un buen número de disciplinas que van desde las ciencias experimentales hasta especulaciones de muy discutible fundamento, pasando por áreas del conocimiento más difícilmente mensurables como la historia y las ciencias sociales.
Podríamos comenzar tomando como primeros factores la fracción de estrellas en la galaxia que presentan planetas en su entorno y la cantidad de estos que tienen la composición adecuada y están en la zona de habitabilidad. Estas son cuestiones que las últimas misiones espaciales como Kepler, Gaia y TESS nos permiten cuantificar. Pisamos tierra firme o, al menos, un suelo más firme de lo que Drake pudo hacer en su momento.
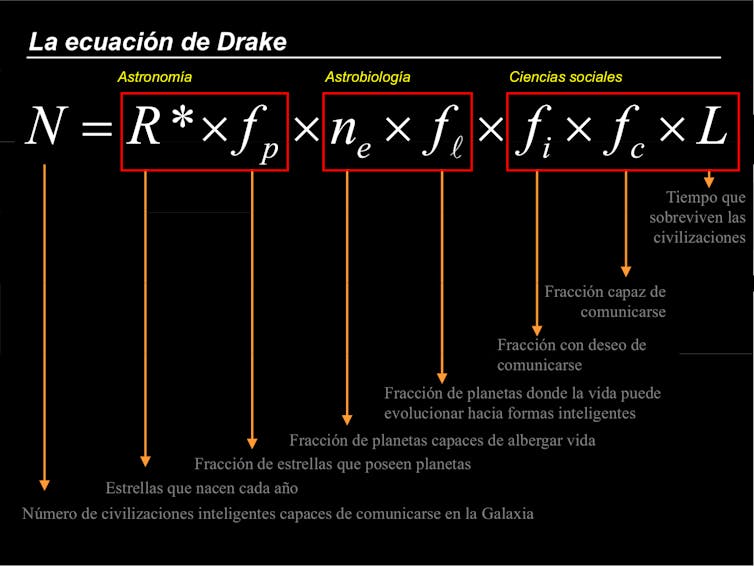 Ecuación de Drake.
Ecuación de Drake.¿Cómo cuantificamos la probabilidad de que surja vida en un planeta que aparentemente reúne las condiciones adecuadas? ¿En cuántos de ellos se ha desarrollado la vida inteligente en forma de civilizaciones? Hasta la fecha, aunque Marte o Venus reunieran condiciones habitables en el pasado, solo conocemos un caso positivo: la Tierra. Ninguno de los más de 4 000 planetas extrasolares conocidos ha demostrado de momento sustentar una biosfera como la nuestra.
A partir de aquí la cuestión se complica. Necesitaríamos cuantificar la evolución de las sociedades hacia la tecnología y el deseo de comunicarse con el resto del universo. También influirá el tiempo durante el cual sean capaces de hacerlo: un siglo, mil años o, como sugirió Drake, hasta 10 000 años. Los datos experimentales para establecer estas cantidades son muy escasos y se basan en la historia humana y en la dinámica de las sociedades que solo comenzamos a comprender de una forma cuantitativa.
En el momento en que Frank Drake asignó valores a todos los términos se encontró con un resultado extraordinario: hasta diez civilizaciones deberían ser detectables mediante SETI. Pero, si así fuera, ¿dónde se encuentran? Esta es la llamada Paradoja de Fermi, opuesta al optimismo de Drake. Encontrar las razones de este inquietante silencio, como se le ha llamado, es también una buena manera de explorar nuestro futuro inmediato y tratar de adivinar los riesgos que como civilización nos pueden esperar a la vuelta de la esquina cósmica.
Otros autores discreparon con los números de Drake desde el primer instante, obteniendo valores mucho más bajos que manifestaban la improbabilidad de lograr el contacto gracias al proyecto SETI. Pequeñas variaciones en los términos que se multiplican en esa larga cadena resultaban en cambios notables del resultado final y, peor aún, las incertidumbres se propagaban exponencialmente en el resultado.
De la ecuación de Drake podemos aprender que los eventos individuales pueden ser realmente infrecuentes o improbables pero, aplicados a una población lo suficientemente grande, su aparición es inevitable. Además, cuando los eventos dependen de una larga cadena de condiciones cuyas probabilidades no podemos estimar con total certeza, nuestra capacidad de predecir los eventos futuros se enturbia. La diferencia con la epidemiología es que, en esta, buscamos que los eventos sucedan en el menor número posible y, para ello, podemos actuar sobre algunos de los factores involucrados.
Desde un punto de vista sanitario, la probabilidad de un evento único, como que enfermemos con síntomas graves, puede ser muy baja, casi despreciable. Aplicada sin embargo sobre el conjunto de la población, terminará sucediendo. Y lo hará más de una vez. Los factores que influyen incluyen la biología, fisiología y la sociología, con una transversalidad similar a la de la astrobiología.
La buena noticia es que cambiar esto se encuentra en nuestra manos: alterando unos pocos factores podemos reducir el número a una cantidad, si no nula, al menos manejable. En ello estamos.![]()
Sobre el autor: Santiago Pérez Hoyos es investigador doctor permanente en astronomía y astrofísica en la Universidad del País Vasco / Euskal Herriko Unibertsitatea
Este artículo fue publicado originalmente en The Conversation. Artículo original
El artículo Lo que la búsqueda de inteligencia extraterrestre nos enseña para entender la pandemia se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La búsqueda de la inteligencia artificial
- Un juego de mesa para entender la irreversibilidad
- La búsqueda de la inteligencia artificial, en la próxima zientziateka
¿Por qué suena triste el modo menor?
Hace cuatro milenios, en Mesopotamia, los sumerios ya utilizaban un sistema musical de siete notas y siete modos para componer sus canciones. Este sistema fue heredado por los griegos que se lo contagiaron al resto de Europa y, desde entonces hasta ahora, —pasando por la larga Edad Media— distintos modos han ido ganando y perdiendo popularidad, según la época. En la actualidad, solemos utilizar preferentemente dos de esos antiguos modos que hemos rebautizado como Modo Mayor y modo menor.
Quizás este desenlace no sea más que un accidente fortuito de la historia. No sabemos si en algún universo paralelo, el reguetón se escribe en el modo frigio y la salsa suena mucho más a mixolidio. Pero, de acuerdo con la hipótesis del profesor David Huron, una vez reducidas las alternativas a dos, su asociación emocional era inevitable: es posible que el modo menor sea, en gran medida un accidente cultural y su asociación con la tristeza deba ser aprendida. Pero esto no significa que sea una asociación arbitraria.
La idea de Huron es que el modo menor suena triste porque suena más triste que el Modo Mayor1. Este, en cambio, saca a relucir su alegría cuando se pone en contraste con su oscuro hermano menor. La clave de esta comparación vuelve a encontrarse en las características de la prosodia humana y cómo esta se ve afectada por nuestras emociones. Pero, para entenderlo, debemos volver a sacar al humano triste de paseo.
Un humano triste, recordemos, es un humano al que le han quitado las pilas. Por eso (y porque tensar las cuerdas vocales también requiere su esfuerzo, aunque no lo parezca), es común que hable bajito, sin cambiar mucho el tono de voz, balbuceando a menudo. Particularmente: es típico que el humano triste produzca sonidos más graves de los que son habituales en él.
Sin embargo, para identificar este cambio en su tono de voz no nos basta con atender a su frecuencia, sin más. Si fuese así, los hombres —que, por lo general, tienen la voz hasta una octava más grave que las mujeres— sonarían siempre tristes, deprimidos, no serían capaces de expresar alegría. Esto, evidentemente, no sucede y el motivo es que, para identificar una voz triste, lo que hacemos es establecer una comparación: entre el tono de esa misma voz en su estado neutro y su tono cuando la invade la tristeza.
Del mismo modo, cuando escuchamos música, realizamos sin darnos cuenta una comparación parecida: entre los tonos que predominan en esa canción y los tonos que se utilizan habitualmente en el resto de nuestra música. O, también, entre los tonos que estamos escuchando en ese momento y los tonos que predominan en el resto de la canción. Y aquí es donde la correspondencia entre los modos Mayor y menor se vuelve relevante, porque si colocamos estas escalas en paralelo, nota a nota, lo que observamos es que el modo menor es una versión oscurecida del Modo Mayor: un modo al que se le han agravado ciertas notas y acortado ciertos intervalos2.
Si bien el uso del modo menor en nuestra tradición musical es, por sí mismo, un accidente cultural, esta especie de tristeza por agravio comparativo parece ser mucho más universal. En 2007, Parag Chordia y Alex Rae quisieron ponerla a prueba utilizando, esta vez, fragmentos musicales procedentes de la India. A través de internet recibieron 22000 respuestas de 500 participantes encargados de clasificar emocionalmente pequeños fragmentos de ragas (los modos melódicos utilizados en la música clásica india). El compendio de todas ellas desvelaba un mismo patrón: los fragmentos con tonos comparativamente más graves e intervalos más pequeños, eran percibidos como más tristes3.
Este es quizás el motivo por el que resulta sorprendente escuchar canciones ya conocidas… a las que alguien ha cambiado el modo (Youtube está lleno de ejemplos). Nuestro recuerdo de la canción original fija un estándar sobre el que inevitablemente superponemos la versión alterada y el contraste saca a relucir la tristeza (o la alegría) percibida
No obstante, mi uso preferido de este contraste se da cuando algún compositor lo establece dentro de una misma canción. Como en esta preciosa canción de El Kanka que, de repente, se quita la ironía y cambia sorpresivamente al modo mayor para hablar de un pasado aparentemente más feliz (se escucha el cambio sobre la misma melodía, en 1’08’’, por ejemplo).
También, me viene a la mente el Lago de los Cisnes de Tchaikovsky. Cuando, en la última escena, después de todo el drama, después de que el tema se haya repetido 500 veces en modo menor, con los protagonistas ya bien muertos y suicidados… el hechizo de los cisnes se rompe y, de repente, escuchamos el mismo tema (2’55’’) ¡pero esta vez triunfante, en Modo Mayor! Parece mentira que pueda tratarse de la misma melodía, cambiando apenas unas pocas notas.
Notas:
1David Huron (2008) A Comparison of Average Pitch Height and Interval Size in Major- and Minor-key Themes: Evidence Consistent with Affect-related Pitch Prosody. Empirical Musicology Review
2El lector que tenga conocimientos musicales quizás se plantee que, al agravar ciertas notas algunos intervalos se harán necesariamente más grandes debido a la estructura cíclica de las escalas. David Huron analizó esta cuestión partiendo de casi 10.000 piezas instrumentales en modo Mayor y menor. Debido a la frecuencia de aparición desigual de los posibles intervalos, el efecto global de cambiar estas notas daba lugar a melodías con intervalos más reducidos en el modo menor.
3Parag Chordia y Alex Rae. “Understanding Emotion in Raag: An Empirical Study of Listener Responses”. Computer Music Modeling and Retrieval. Sense of Sounds, 2008.
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo ¿Por qué suena triste el modo menor? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:La hoja de papel con cuatro caras, una propuesta de taller
Hace unos cuantos días, pensando en la situación de confinamiento en la que nos encontramos en estos momentos, me pareció que sería una buena idea preparar una actividad sencilla para enviar a la gente y que pudieran realizarla en su casa. Mi idea era que fuese una actividad para personas de cualquier edad, desde pequeños (acompañados si es necesario) hasta mayores. Entonces, me decidí por un taller que hago desde hace algunos años, aunque relacionado con otras cuestiones, y que me gusta mucho. Consiste en construir un objeto matemático sencillo y sorprendente, una hoja de papel con cuatro caras.
Este objeto matemático, cuyas instrucciones de construcción os voy a explicar en esta entrada del Cuaderno de Cultura Científica, pertenece a la familia de objetos llamados flexágonos y que fue descubierta por el matemático inglés Arthur Stone, de quien ya hemos hablado en relación con el problema de la cuadratura del cuadrado en 1939. Aunque estos objetos fueron dados a conocer y popularizados por el gran divulgador de las matemáticas Martin Gardner (1914-2010) en su columna Juegos matemáticos de la revista Scientific American. En concreto, el objeto matemático que vamos a construir en esta entrada es un tetraflexágono, es decir, un flexágono con cuatro lados (cuadrado o rectángulo), además, como va a poder mostrar cuatro caras, se denomina un tetratetraflexágono.
 Portadas de los dos primeros libros de Martin Gardner en los que se recogen los artículos de su columna Juegos matemáticos en la revista Scientific American. En el primero aparece su artículo Hexaflexagons y en el segundo Tetraflexagons
Portadas de los dos primeros libros de Martin Gardner en los que se recogen los artículos de su columna Juegos matemáticos en la revista Scientific American. En el primero aparece su artículo Hexaflexagons y en el segundo Tetraflexagons
Pero vayamos directamente a nuestro objeto matemático, esa hoja de papel de cuatro caras, el tetratetraflexágono, y a su construcción: materiales e instrucciones.
Material básico para el taller: una hoja de papel normal, por ejemplo, din A4, un lápiz y una regla.
Instrucciones para construir el tetratetraflexágono, la hoja de papel con cuatro caras:
Punto 1. Tomamos la hoja de papel, que colocamos con el lado largo en horizontal, y lo vamos a dividir –por delante y por detrás- en cuatro columnas y tres filas, utilizando líneas trazadas con un lápiz. Generando de esta forma 4 x 3 = 12 casillas rectangulares en cada lado.
Punto 2. En cada una de las casillas vamos a pintar, centrado, un número. En las 12 casillas de la parte frontal pintamos los números 4, 4, 3, 2 (en la primera fila, la de arriba), luego 2, 3, 4, 4 (en la segunda fila, en medio) y 4, 4, 3, 2 (en la tercera). Ahora en las casillas de la parte trasera pintamos los números 1, 1, 2 y 3 (arriba), 3, 2, 1, 1 (en medio), 1, 1, 2, 3 (abajo). Ojo, aquí quien lo desee puede echarle imaginación y pintar unos números chulos.
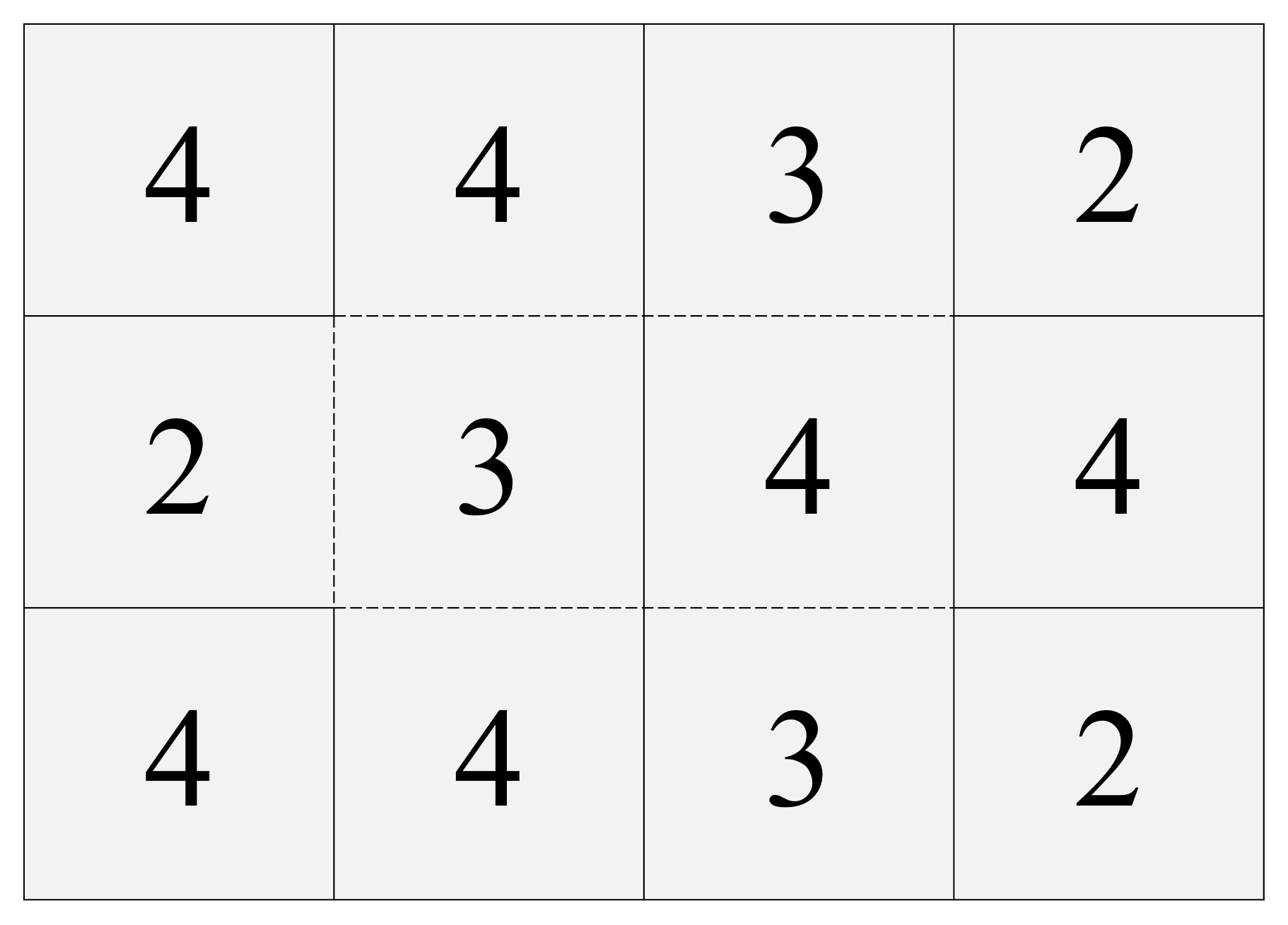 Números de las doce casillas de la parte frontal del folio original
Números de las doce casillas de la parte frontal del folio original
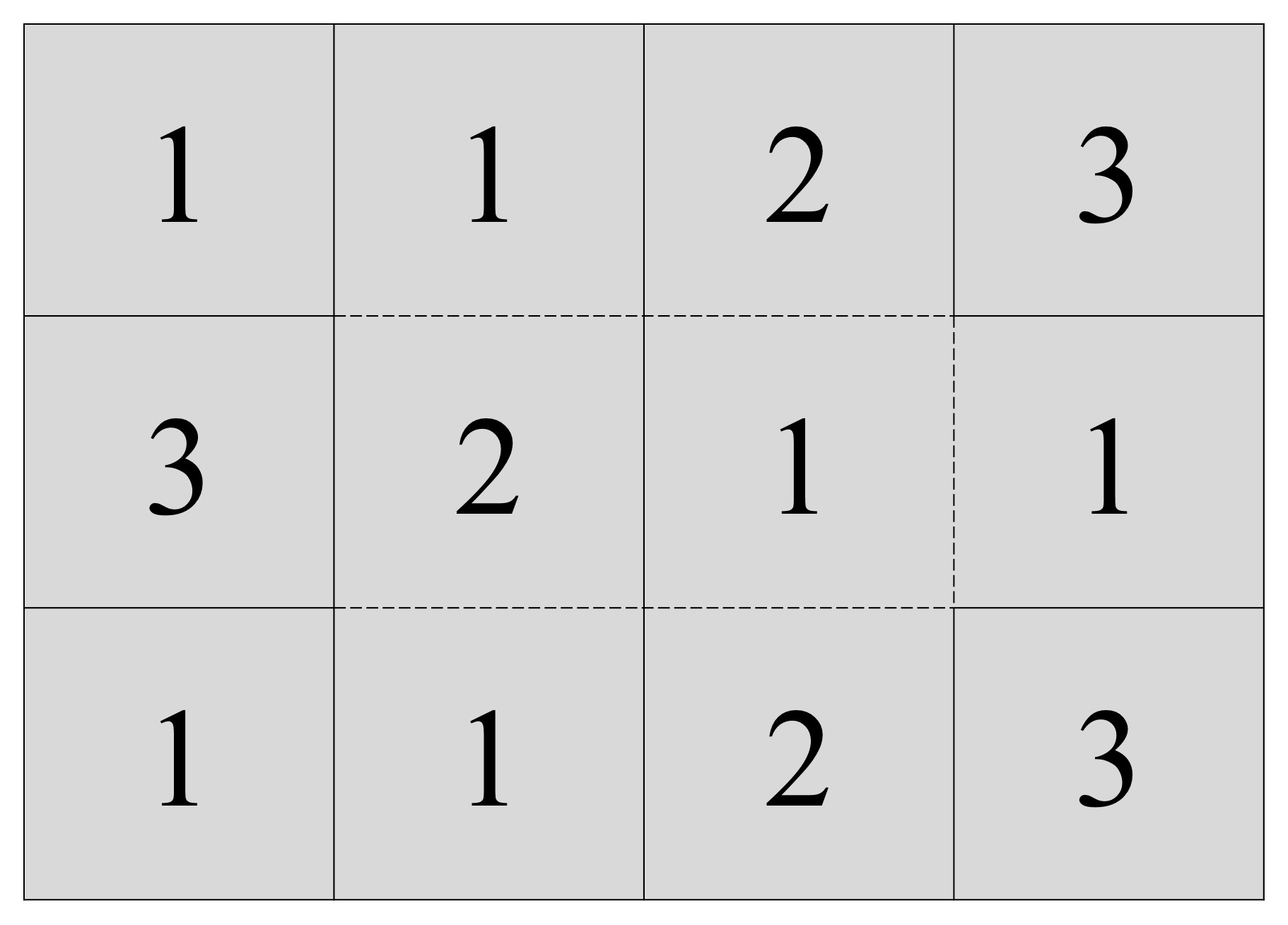 Números de las doce casillas de la parte trasera del folio original
Números de las doce casillas de la parte trasera del folio original
Punto 3. Ahora tenemos que realizar un pequeño corte con unas tijeras, por lo tanto, hay que tener cuidado. Si la actividad la realizan niños y niñas pequeños necesitarán la ayuda, o supervisión, de una persona mayor. Antes de realizar el corte, doblad por las líneas rectas que habéis pintado a lápiz, os ayudará a realizar el corte y además es necesario para la parte final.
Pero vayamos con el corte. Si consideramos la hoja de papel con la parte frontal, la primera, la que tiene solo doses, treses y cuatros, entonces vamos a cortar el papel para separar las dos casillas del centro –con los números 3 y 4- del resto, pero por todos los lados, salvo uno, el derecho –donde se unen los dos cuatros (véase la siguiente imagen).
Es decir, cortaremos los lados de arriba de las casillas centrales, 3 y 4, el lado izquierdo de la casilla del 3 y los lados de debajo de esas dos casillas centrales. De esta forma, estas dos casillas, 3 y 4, que están unidad entre sí, solo están unidas al resto por el lado derecho, el lado entre los dos cuatros.
Punto 4. A continuación, vamos a realizar unos cuantos dobleces para generar nuestra nueva hoja de papel, que tendrá 2 x 3 = 6 casillas.
Primero, doblamos esa parte central, de dos casillas, hacia la derecha, de forma que va a quedar un 2 hacia arriba, donde estaba el 4, y el 1 que lo acompaña quedará por debajo de la hoja.
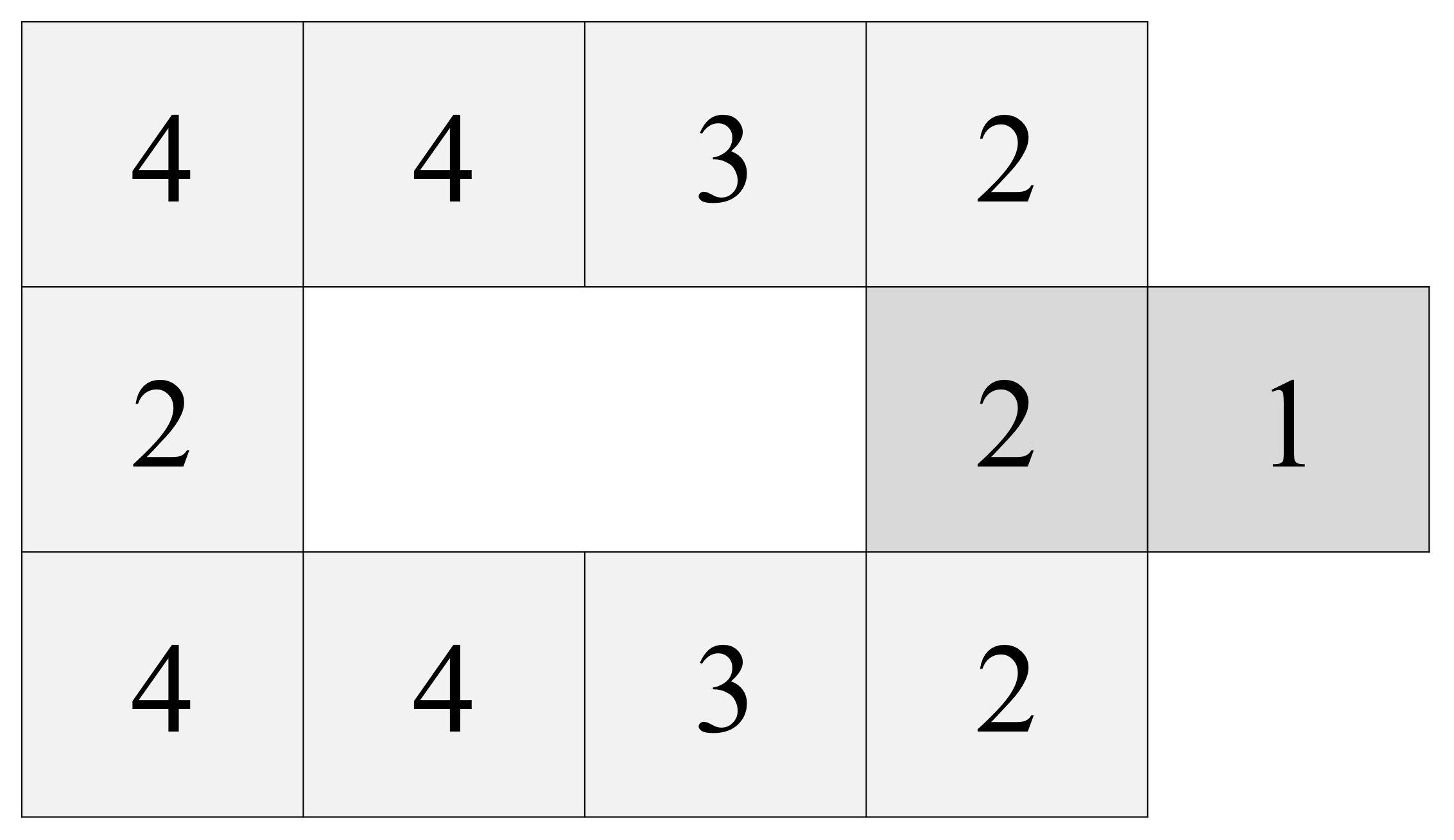
Después, doblamos la columna 4, 2, 4 hacia la derecha, una vez, y después toda la nueva columna (sobre la que ahora vemos los números 3, 1, 3) de nuevo hacia la derecha.
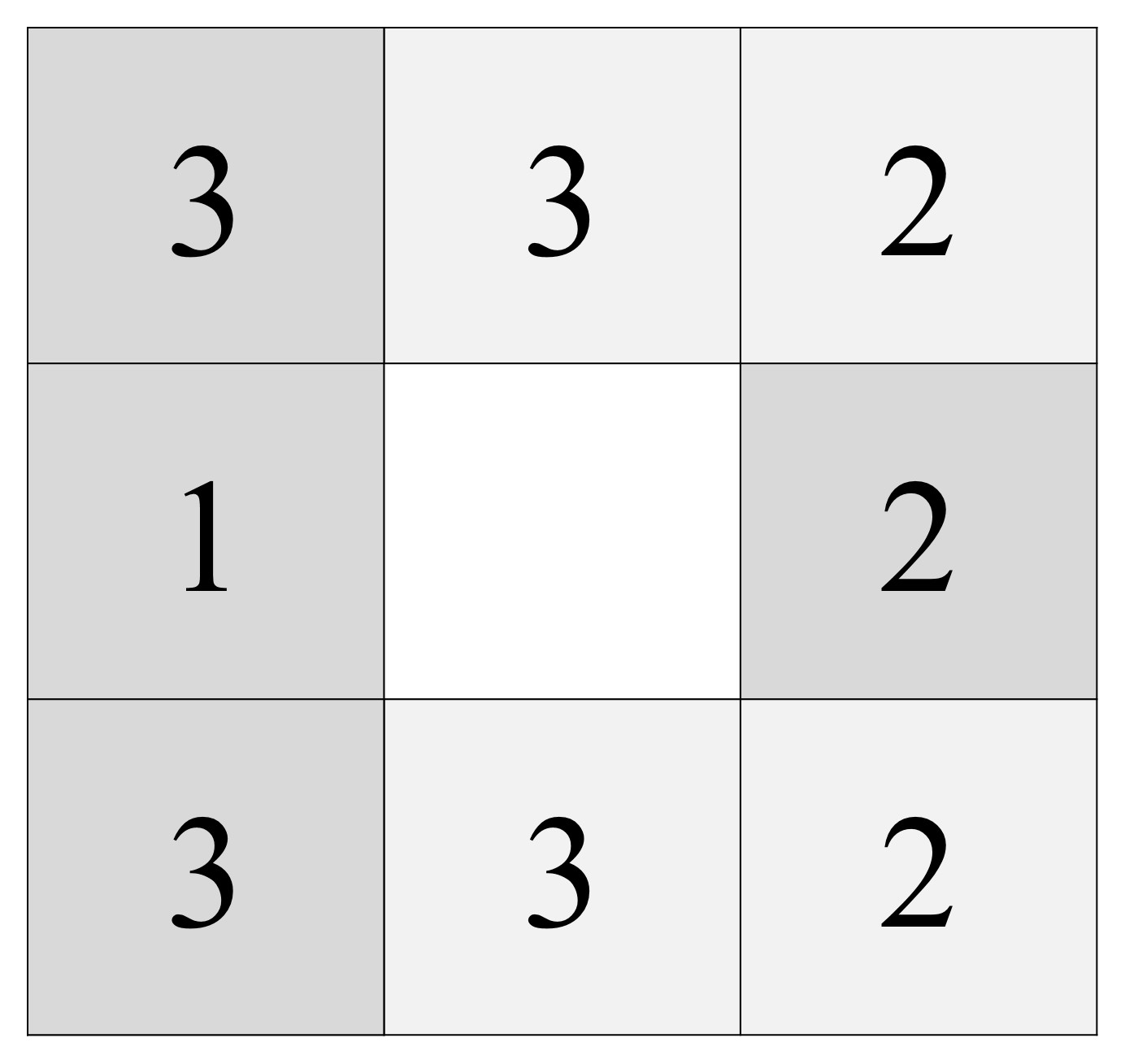
Nos quedará una hoja de papel con 2 x 3 = 6 casillas, con un 2 en todas las casillas, como muestra la siguiente imagen.
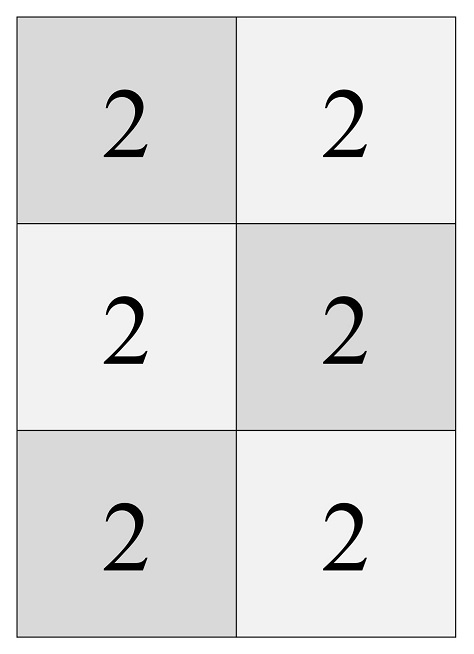
Punto 5. Si le dais la vuelta a la nueva hoja de 6 casillas, tendréis una hoja de papel con un 1 en todas las casillas (la imagen de abajo). Estamos entonces en el último paso. Hay que poner un poco de celo uniendo los dos unos de la fila del centro, el de la izquierda con el de la derecha.
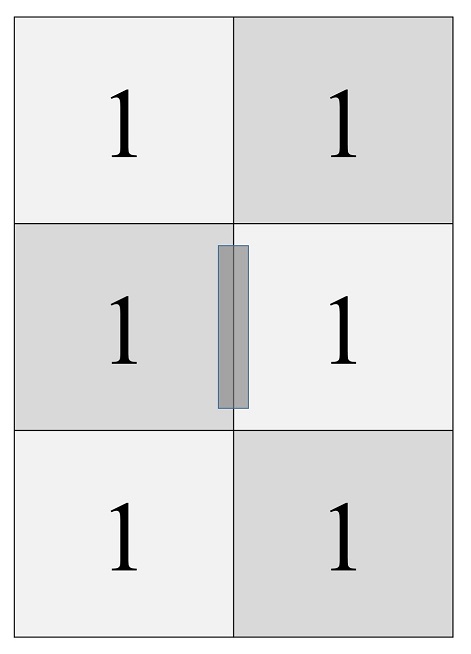
Y ya tenéis la “nueva” hoja de papel con cuatro caras. Veámoslo. En la que tenemos delante solo hay unos (1), le damos la vuelta y solo hay doses (2), luego dos caras. Ahora, con los doses mirando hacia nosotros, doblaremos la hoja por la mitad vertical, llevando las dos mitades hacia atrás, y cuando lleguemos a juntar las dos partes veremos que se nos abre la hoja por el medio, la ayudamos a abrirse con nuestros dedos y veremos que la hoja que tenemos delante tiene todo treses (3).

Si volvemos a doblar la hoja por la mitad vertical, hacia atrás, descubriremos una nueva cara con todo cuatros (4). Es decir, tenemos una hoja de papel con cuatro caras, un tetratetraflexágono. Solo un consejo, antes de mostrárselo a las demás personas practicad el paso de una cara a otra.
La parte básica del taller es la que acabamos de describir arriba, pero a partir de ahí cada cual puede echarle imaginación y hacer el flexágono lo más artístico o curioso que considere oportuno. Por ejemplo, Cristina Barcala, una apasionada de la divulgación científica y lectora del Cuaderno de Cultura Científica, nos mandaba su propia versión, de tamaño mini (la siguiente imagen).

Aunque si os ha gustado esta actividad sobre la realización de un tetraflexágono, podemos abordar la realización de los otros dos tetraflexágonos que aparecen en el artículo Tetraflexagons, del libro de Martin Gardner The 2nd Scientific American Book of Mathematical Puzzles and Diversions (1961), uno de tres caras –tritetraflexágono- y otro de seis caras –hexatetraflexágono-.
Empecemos con el tritetraflexágono. Para realizarlo hay que construir con una hoja de papel una “tira de papel” de dos filas, como la que aparece en la siguiente imagen, trazar las seis casillas de cada cara y dibujar los números 1, 2 y 3 en las casillas, de la parte frontal y trasera, como aparece en la imagen.
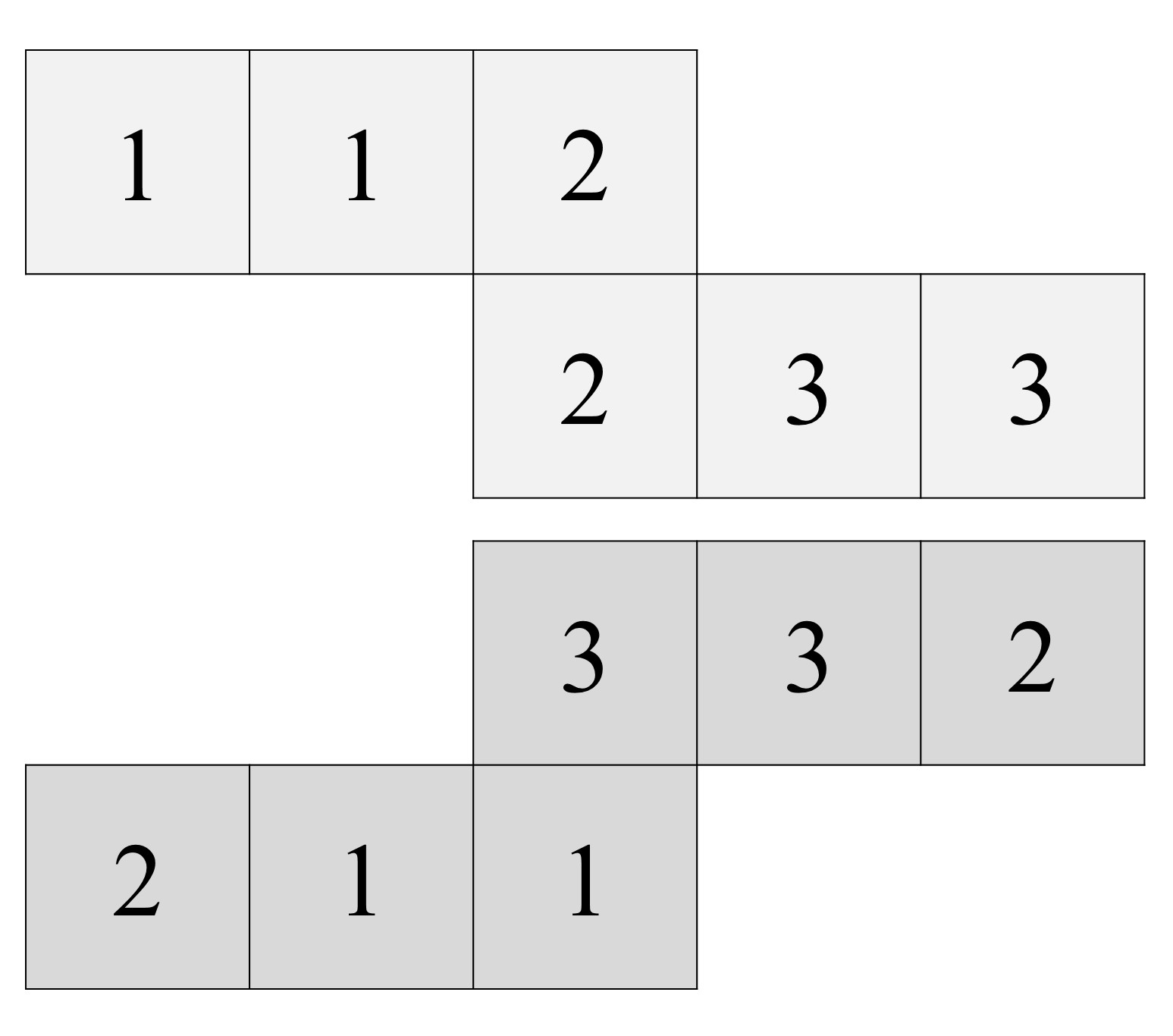
Después doblamos hacia atrás las dos casillas de la izquierda, las que tienen los unos, quedando nuestra tira de papel como se ve en la imagen.
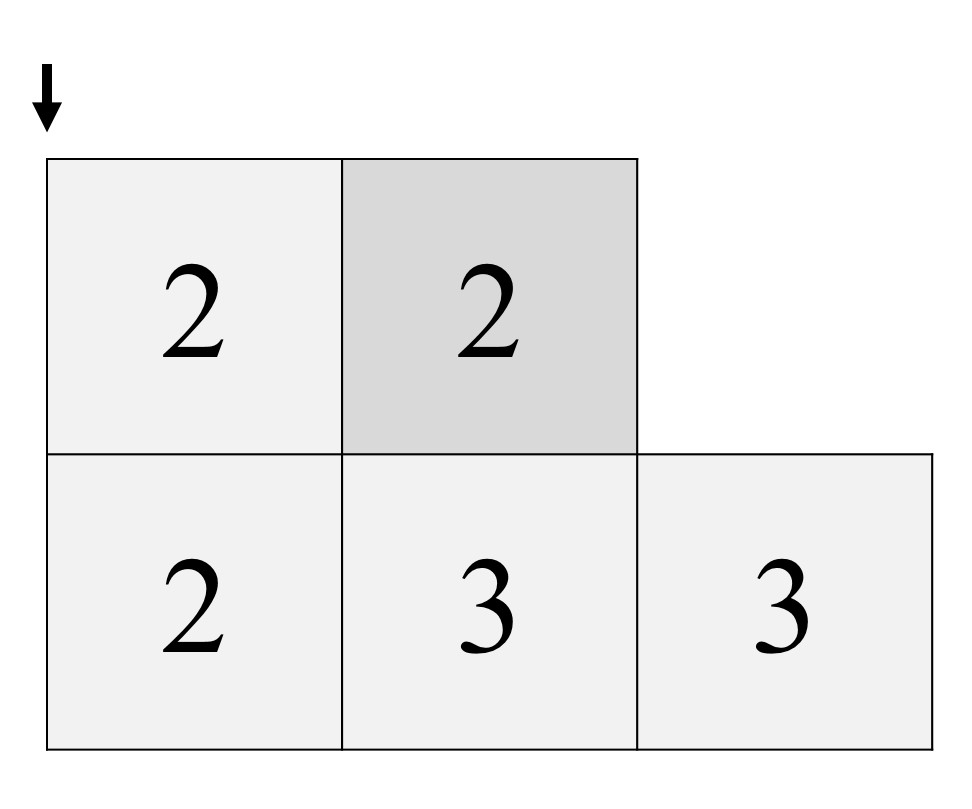
Y doblamos, ahora hacia delante, la casilla de la derecha, la que tiene el tres, quedando así todas las casillas con doses frente a nosotros.
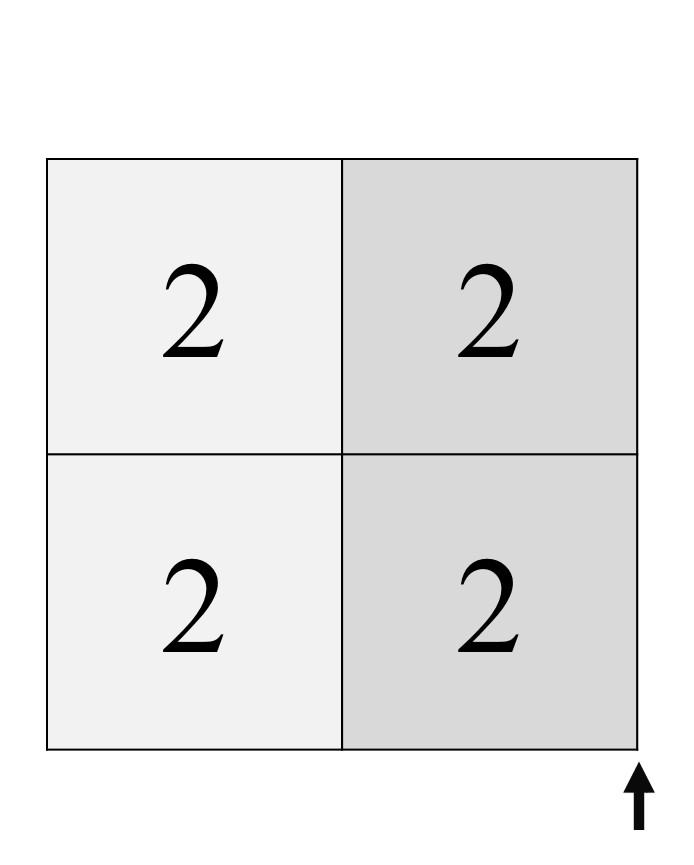
Para finalizar, solo hay que colocar un pequeño trozo de celo entre las dos casillas de la derecha, como se muestra en la imagen.
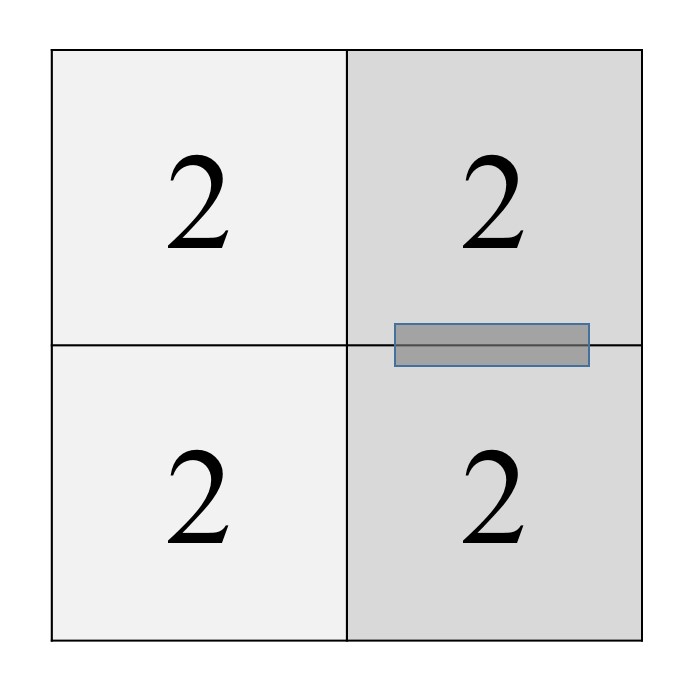
De esta forma, hemos construido el tritetraflexágono, que tiene tres caras, podemos mostrar en cada una de esas caras, todos unos, doses o treses.
Por último, vamos a terminar con los esquemas para realizar el hexatetraflexágono. Para este flexágono, partimos de una hoja cuadrada, dividida en 16 casillas –cuatro filas y cuatro columnas- en cada cara, a la que le hemos cortado las cuatro casillas del centro. Luego solo le quedan las 12 casillas del exterior. Esta vez vamos a utilizar seis colores (aunque mantenemos los números para seguir las instrucciones de la construcción) para pintar cada casilla, de la parte frontal y trasera, como aparece en las siguientes imágenes.
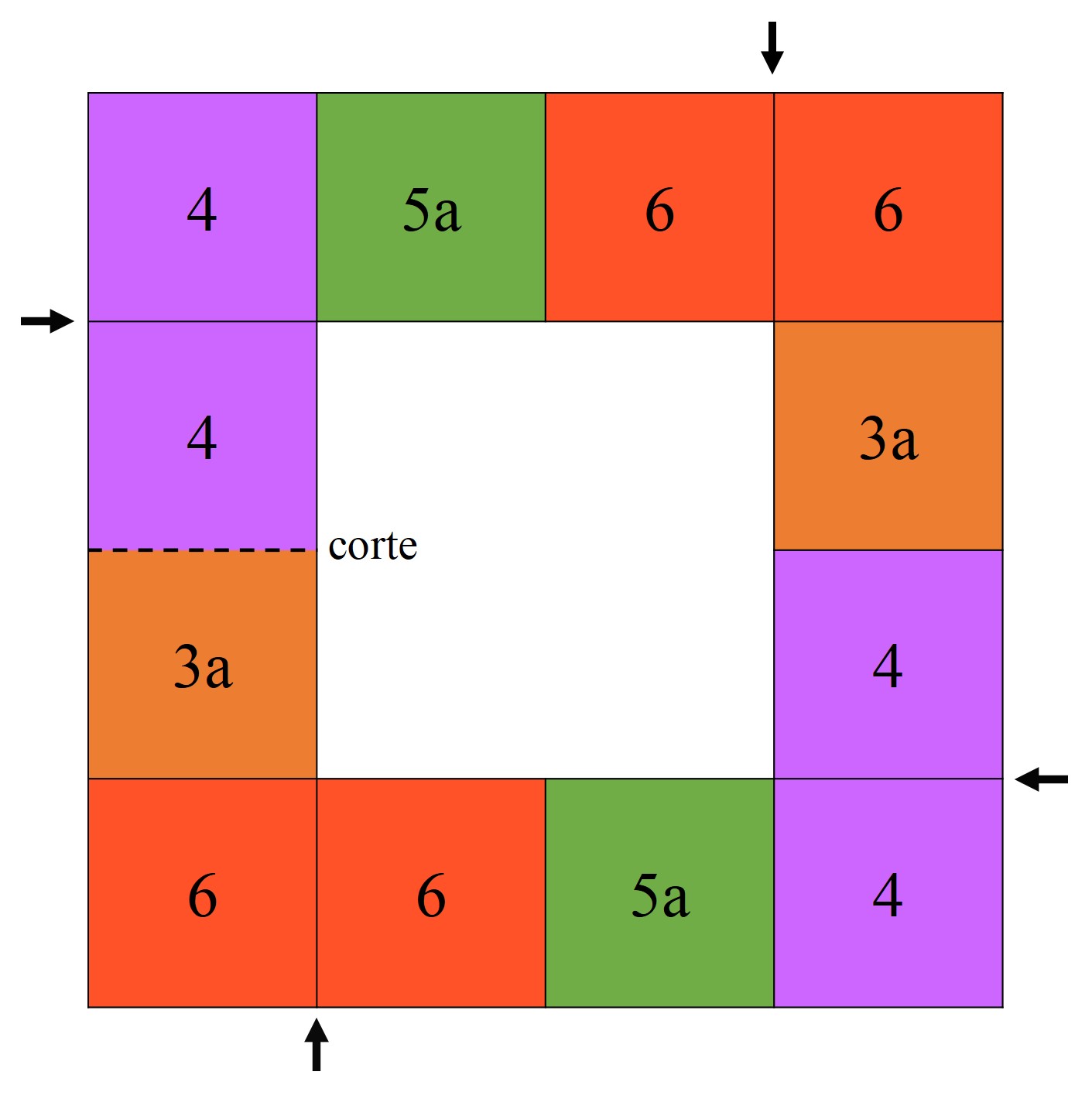
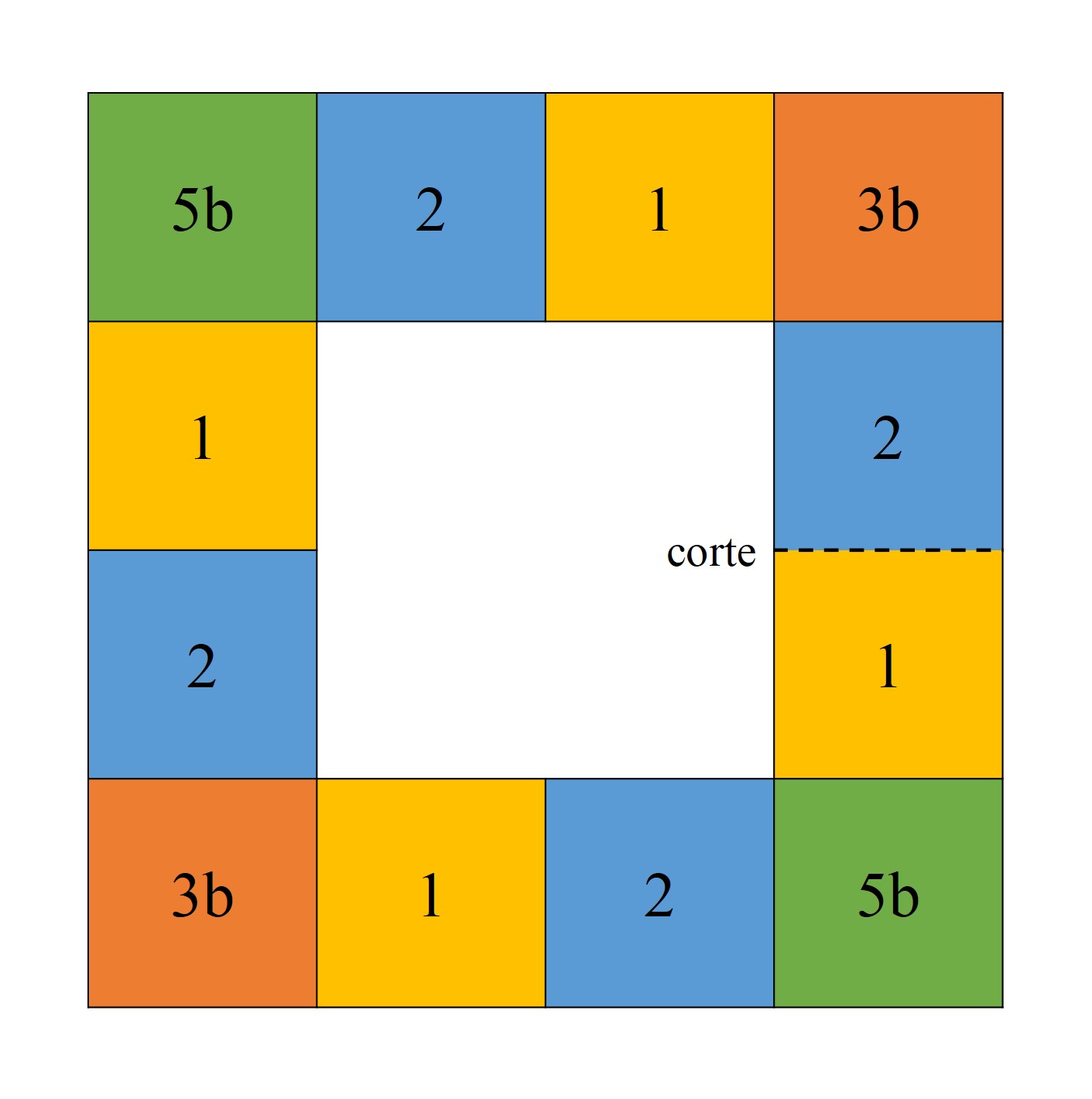
Las dos casillas de la derecha (en la primera imagen) se separan con un pequeño corte horizontal. Entonces, vamos doblando por donde indican las flechas, empezando por la flecha de abajo y en el sentido de las agujas del reloj, de forma que lo que nos queda al terminar es la siguiente imagen.

De nuevo, doblamos por donde indican las flechas, hasta que quede como la siguiente imagen. Para terminar, solamente hay que añadir un trozo de celo para unir, por arriba, la casilla superior izquierda de delante, con la que tiene atrás.

Y ya tendríamos nuestro hexatetraflexágono.
Bibliografía
1.- Martin Gardner, The 2nd Scientific American Book of Mathematical Puzzles and Diversions, University of Chicago Press, 1987 (publicado originalmente en 1961).
2.- Robert Ghattas, Bricológica, Treinta objetos matemáticos para construir con las manos, RIALP, 2011.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo La hoja de papel con cuatro caras, una propuesta de taller se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El teorema de los cuatro colores (3): Tras más de un siglo de aventura… ¿un ordenador resuelve el problema?
- El teorema de los cuatro colores (2): el error de Kempe y la clave de la prueba
- Cuatro leyes consumadas siguiendo una banda de Möbius
La teoría de bandas explica la conducción eléctrica
 Foto de Josep Castells / Unsplash
Foto de Josep Castells / UnsplashLa idea básica tras las bandas de Bloch en un sólido es que se crean al unirse los estados cuánticos de los átomos individuales. Bloch y otros ampliaron y refinaron la teoría de bandas de los sólidos durante la década de 1930, hasta el punto de que explica muy bien el comportamiento de conducción eléctrica de los distintos materiales.
Cuando los átomos se unen en un cristal, cada uno de los estados cuánticos individuales de los átomos se une con los estados correspondientes en otros átomos (idénticos) en el cristal para formar las diversas bandas de energía dentro del material. De hecho, si hay un total de N átomos idénticos en el material, entonces hay N estados cuánticos dentro de cada banda. Los electrones en los átomos llenan los estados disponibles dentro de cada banda. Así, si hay N estados en una sola banda, puede haber hasta 2N electrones en cada banda [1].
La física interesante ocurre en la parte superior de las bandas llenas. Cuando se aplica un campo eléctrico externo (voltaje) al material, un electrón puede responder al campo solo si puede moverse a un estado cuántico ligeramente más alto, ya que tendría un poco más de energía al ser afectado por el campo. Esto será posible solo si hay algunos estados libres cercanos a los que el electrón pueda saltar. Este es el caso de los materiales conductores, como el cobre y la plata, ya que sus electrones se llenan en los estados disponibles de modo que la banda más alta está llena solo parcialmente. Los electrones en esta banda, que se llama banda de conducción, son libres de ser conducidos (en realidad, propagados como ondas) por el material, ya que hay estados cuánticos vacíos cercanos en su banda de energía. Pero los electrones en las bandas inferiores llenas no pueden moverse, ya que no hay estados libres cerca.
Por otro lado, si las bandas se llenan de manera que se ocupa exactamente el límite superior de una banda, entonces los electrones no pueden responder a un campo eléctrico, ya que hay una brecha de energía [2] que les impide llegar a un estado cuántico en el que pueden moverse libremente [3]. Un material con estas características es lo que conocemos como aislante. [4]
Finalmente, si estamos ante un caso como el de los aislantes pero la brecha de energía con la banda de conducción no es demasiado grande, puede resultar que la energía térmica sea suficiente como para que algunos electrones salten a ella. Este es el caso de los semiconductores.
Notas:
[1] De acuerdo con una regla en la mecánica cuántica solo dos electrones pueden ocupar un estado de energía cuántica de un solo átomo. El principio de exclusión de Pauli establece que no pueden existir dos partículas en un sistema, electrones en un átomo o quarks en un hadrón, que tengan un conjunto de números cuánticos idéntico. Aplica solo a las partículas llamadas fermiones, no a los hadrones. Los electrones son en todo iguales e indiscernibles salvo porque unos tiene una “cosa” llamada espín con un valor y otros con otro valor. Por eso solo puede haber dos electrones en un estado cuántico de energía: en ese estado todos los números cuánticos son iguales salvo el espín, si hubiese un tercer electrón se violaría el principio de exclusión. Aunque parece un principio inventado para que cuadren los datos, se justifica por el teorema de la estadística del espín de la teoría cuántica de campos relativista.
[2] Una «banda prohibida» por la naturaleza cuántica de las bandas.
[3] Normalmente. Si el voltaje es enorme algunos electrones podrán desplazarse, porque adquirirán energía suficiente como para saltar de la banda de valencia a la banda de conducción. Véase [3]
[4] Un ejemplo es el diamante, en el que el estado cuántico lleno más alto también llena una banda de energía. Esta banda se llama banda de valencia, ya que está ocupada por los electrones de valencia externos de los átomos. La brecha de energía a la siguiente banda, que está vacía, es de aproximadamente 6 eV, por lo que los electrones en el diamante normalmente no pueden alcanzar la banda de conducción y, por lo tanto, el diamante es un buen aislante. En los conductores la banda de conducción se solapa con la llamada banda de valencia, por lo que no hay brecha de energía.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo La teoría de bandas explica la conducción eléctrica se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Las bandas de Bloch
- La teoría de bandas de los sólidos se hace topológica
- El modelo de Bohr explica las regularidades en el espectro del hidrógeno
Los males de la ciencia tienen remedio
 Foto: Vlad Tchompalov / Unsplash
Foto: Vlad Tchompalov / UnsplashEn las anotaciones precedentes nos hemos dedicado a repasar los que a nuestro juicio son los males de la ciencia actual. La serie empezó por una presentación de la empresa científica, el marco institucional y económico en el que se desarrolla, y el entramado de las publicaciones científicas como producto principal. Seguimos analizando los valores de la ciencia tal y como los formuló Merton a mediados del siglo pasado. Y a continuación abordamos el repaso de una serie de males que pueden considerarse propios, específicos de la empresa científica. Las últimas anotaciones han tratado de las resbaladizas relaciones entre investigación científica y ética en diferentes planos.
La relación de “males” o “patologías” no ha pretendido ser exhaustiva. Algunas de las malas prácticas presentadas aquí lo son porque vulneran las normas de Robert K Merton, incumplen el ethos de la ciencia en los términos en que él lo definió y que, implícitamente, asumimos gran parte de los científicos. Otras tienen más que ver con aspectos nucleares de la práctica científica o con el sistema de publicaciones o de financiación de la investigación. Son, por lo tanto, diferentes y seguramente los remedios que requieran también lo sean. Pero sospechamos que una gran parte de los problemas se atenuaría si universidades y centros de investigación modificasen el sistema de incentivos que utilizan para reconocer y premiar el trabajo de su personal científico. La cantidad debería perder importancia como criterio, para ir valorando cada vez más la calidad del trabajo y la trascendencia o relevancia de las investigaciones. No se trata de acudir a indicadores de las publicaciones tal y como se utilizan hoy o, al menos, no solo a esos indicadores (basados en métricas de impacto y similares), sino de recurrir a la valoración experta del nivel y alcance del trabajo realizado.
Tenemos por último, todos esos ámbitos en los que el desarrollo de la ciencia se enfrenta a dilemas de naturaleza ética. No se trata de dilemas específicos de la ciencia, o dilemas cuya resolución deba recaer exclusivamente sobre el mundo científico. Son, en su gran mayoría, dilemas sociales. La ciencia es, si acaso, el instrumento, pero es en el ámbito social y político donde se han de resolver. Si se han de exprimir al máximo las posibilidades que nos brinda la biotecnología, o si debemos permanecer pasivos ante la previsible robotización de la sociedad, son cuestiones que no corresponde dirimir a los científicos. Quienes hacen la investigación científica deberán aportar su criterio experto, y tanto la sociedad como los responsables deberían tomar buena nota y tener en cuenta el dictamen experto, pero en última instancia, las decisiones son de carácter social y político. Nos interesa remarcar esta diferencia, porque los males que hemos considerado intrínsecos a la ciencia lo son porque de no neutralizarlos, está en juego el propio funcionamiento del sistema científico, y en ese terreno, los miembros de ese sistema tenemos mucho que decir y que hacer. Precisamente por esa razón, no nos parece saludable que los científicos se desentiendan de las implicaciones sociales de su trabajo. Creemos que tenemos una especial responsabilidad al respecto, precisamente porque somos quienes mejor podemos calibrar el alcance de nuestro trabajo más allá de cómo quede recogido en las publicaciones científicas.
La ciencia sufre de esos y de otros males; son males serios y de graves consecuencias. Las que afectan, con carácter general, al desarrollo del conocimiento son evidentes. Pero esas no son las únicas. También hay consecuencias prácticas de gran trascendencia. En los Estados Unidos se estima que la investigación preclínica no reproducible tiene un coste anual de 28 mil millones de dólares y, por supuesto, retrasa el desarrollo de tratamientos que salvan vidas humanas y mejoran la calidad de vida. Es de suponer que en el resto de potencias científicas las cosas estarán, en su correspondiente proporción, más o menos igual.
Hay investigadores que son reticentes a abordar de forma abierta estas cuestiones, porque temen que pueden conducir a un debilitamiento de la empresa científica porque la sociedad deje de confiar en los científicos. Creo que se trata precisamente de lo contrario. La opacidad sería contraproducente. Una herida que se cierra sin haberla limpiado debidamente, se cierra en falso porque cultiva la infección en su interior y antes o después, aflorará. La vía más eficaz para sanar los males pasa por conocerlos y buscar las medidas para combatirlos. No hay que ser tan ingenuo como para pensar que muchos de los problemas aquí expuestos tienen una solución definitiva. Ningún problema complejo suele tener soluciones definitivas y, desde luego, nunca son soluciones simples. De lo que se trata es de conseguir un funcionamiento de la empresa científica razonablemente mejor que el actual, más sano, con mejores resultados, más eficiente, y que se base más en la realización de interesantes trabajos que en la producción de ingentes cantidades de artículos.
Pero a la vez que han de preocuparnos los males, también debemos congratularnos de que sea la misma comunidad científica la que está tratando de aportar soluciones. Porque han sido científicos profesionales quienes han investigado y dado a conocer las patologías que aquejan a la práctica científica. Han sido científicos profesionales y organizaciones científicas las que han propuesto medidas para afrontar los problemas y resolverlos. Y algunas revistas científicas están adoptando medidas para incentivar la transparencia y la reproducibilidad de los resultados. Esas son las buenas noticias.
Fuentes:
Agin, D (2007): Ciencia basura. Starbooks, Barcelona.
Briggle, A (2012): Scientific Responsability and Misconduct, in Encyclopedia of Applied Ethics, Vol 4, pp.: 41-48, 2nd edition, Academic Press, London
Ferris, Timothy (2010): The Science of Liberty, Harper Collins, Nueva York
Fischer, B A, Zigmond, M J (2012): Scientific Publishing, in Encyclopedia of Applied Ethics, Vol 4, pp.: 32-40, 2nd edition, Academic Press, London
Häyry, M (2012): Genetic Engineering of Human Beings, in Encyclopedia of Applied Ethics, Vol II, pp.: 437-444, 2nd edition, Academic Press, London
Holm, S, Stokes E (2012): Precautionary Principle, in Encyclopedia of Applied Ethics, Vol III, pp.: 569-575, 2nd edition, Academic Press, London
Johnson, J (2012): Ethical Experiments, in Encyclopedia of Applied Ethics, Vol 2, pp.: 149-156, 2nd edition, Academic Press, London
Johnson, S (2012): Nanotechnology, in Encyclopedia of Applied Ethics, Vol III, pp.: 183-185, 2nd edition, Academic Press, London
López Nicolás, J M (2016): Vamos a contar mentiras. Cálamo, Madrid.
Menéndez Viso, A (2005): Las ciencias y el origen de los valores. Siglo XXI.
Merton, R K (1942): “Science and Technology in a Democratic Order” Journal of Legal and Political Sociology 1: 115-126. [Traducción al español como “La estructura normativa de la ciencia” en el volumen II de “La Sociología de la Ciencia” Alianza Editorial 1977, traducción de The Sociology of Science – Theoretical and Empirical Investigations, 1973]
Neri, D (2012): Eugenics, in Encyclopedia of Applied Ethics, Vol 1, pp.: 189-199, 2nd edition, Academic Press, London
Oreskes, N y Conway, E N (2018): Mercaderes de la duda. Cómo un puñado de científicos oscurecieron la verdad sobre cuestiones que van desde el humo del tabaco al calentamiento global. Capitán Swing, Madrid.
Resnik, D B (2012): Developing World Bioethics, in Encyclopedia of Applied Ethics, Vol 1, pp.: 771-778, 2nd edition, Academic Press, London
Solbakk J H, Vidal, S M (2012): Research Ethics, Clinical, in Encyclopedia of Applied Ethics, Vol 3, pp.: 775-785, 2nd edition, Academic Press, London
Spier, R E (2012): Science and Engineering Ethics, Overview, in Encyclopedia of Applied Ethics, Vol 4, pp.: 14-31, 2nd edition, Academic Press, London
Di Trocchio, F (1993): “Las mentiras de la ciencia” Alianza Editorial.
Ziman, J (2000): Real Science: What It Is and What It Means. Cambridge University Press.
Zuk, M (2013): Paleofantasy: What Evolution Really Tells Us about Sex, Diet, and How We Live. Norton & Co, New York.
Este artículo se publicó originalmente en el blog de Jakiunde. Artículo original.
Sobre los autores: Juan Ignacio Perez Iglesias es Director de la Cátedra de Cultura Científica de la UPV/EHU y Joaquín Sevilla Moroder es Director de Cultura y Divulgación de la UPNA.
El artículo Los males de la ciencia tienen remedio se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- No todo vale al servicio de la ciencia
- Dilemas éticos en la frontera de la ciencia
- No todas las personas tienen las mismas oportunidades de dedicarse a la actividad científica
Van Eyck al descubierto

Antes de convertirse en el año de la pandemia 2020 iba a servir para homenajear a dos de los pintores más importantes de todos los tiempos: Jan van Eyck y Rafael Sanzio. Hagamos de este espacio un refugio y disfrutemos del arte de estos dos genios durante las próximas entregas. Por deferencia, comenzaremos por el que nació primero. De este modo nos sumamos al tributo que se le estaba rindiendo a van Eyck en Gante, donde se guarda una de sus más emblemática obras: La adoración del cordero Místico. La ciudad belga lucía sus mejores galas y bajo el lema “OMG! Van Eyck was here” había preparado una serie de eventos, incluyendo una exposición de pinturas del artista flamenco como nunca antes se había visto. Afortunadamente las nuevas tecnologías nos permiten disfrutar de estas obras sin tener que salir de casa.
Los “primitivos” flamencos
Jan van Eyck y su hermano mayor Hubert fueron, junto a Robert Campin, los primeros de un grupo que ha pasado a la historia del arte con el nombre de los primitivos flamencos. Tomemos ese adjetivo en el sentido de que fueron unos pioneros y no en referencia a un estilo poco desarrollado. ¿Os atreveríais a decir eso de alguien que hace las virguerías que os muestro en la Imagen 1? En la primera mitad del s. XV estos pintores fueron dejando atrás el estilo gótico internacional entonces imperante, en pos de una nueva forma de entender la pintura. Pese a que se trata de un momento crucial de la historia del arte, se ha visto un tanto eclipsado por el coetáneo Renacimiento italiano. A favor de los maestros flamencos hemos de decir que en ciertos aspectos técnicos igualaban o superaban a los italianos, aunque sus nombres no sean tan conocidos como el de Donatello o el de Leonardo, por poner dos ejemplos.
 Imagen 1. Virgen del Canónigo Van der Paele (122×158 cm) y detalles. Fuente: http://closertovaneyck.kikirpa.be, © KIK-IRPA, Brussels.
Imagen 1. Virgen del Canónigo Van der Paele (122×158 cm) y detalles. Fuente: http://closertovaneyck.kikirpa.be, © KIK-IRPA, Brussels.El florecimiento de este estilo en la región de los Países Bajos no fue por casualidad. A principios del s. XV urbes como Brujas o Gante habían prosperado gracias al comercio y a la artesanía. Por lo tanto, a la nobleza y al clero se le sumaba una incipiente burguesía con ganas de demostrar su estatus social. En ese entorno destacó Jan van Eyck, quien tras trabajar en diferentes ciudades se instaló en 1425 en la corte de Felipe el Bueno, duque de Borgoña, la gran potencia de la zona en aquel momento. Desde esa fecha hasta su muerte en 1441 realizó las obras que le han colocado en el Olimpo de la pintura. Si algo destaca en van Eyck, más allá de su brillante técnica, es su capacidad de innovación: fue todo un pionero. Su contribución más importante fue la pintura al óleo. Aunque no inventó esta técnica como se afirma en ciertas partes, la perfeccionó y ayudó a popularizarla. Hasta entonces la pintura al temple era la más habitual, pero la posibilidad de aglutinar los pigmentos con aceites abrió nuevas posibilidades, sobre todo gracias a las veladuras, capas de pintura semitransparentes que permiten dar matices y crear juegos de luces.
Pero van Eyck fue mucho más que el adalid de la pintura al óleo. También tuvo la capacidad de incorporar el paisaje a sus obras, otorgándoles sensación de profundidad en una suerte de perspectiva atmosférica previa a Leonardo (Figura 2A). Trataba los detalles con una meticulosidad absoluta, posiblemente debido a su pasado como pintor de miniaturas (Figura 2B), y sus óleos recogen hasta el más mínimo pliegue y ornamento de las sofisticadas lanas flamencas o las alfombras orientales. No había ilusión óptica que se escapase a sus afilados pinceles. Una buena muestra es el Díptico de la Anunciación del Museo Thyssen en el que el Arcángel y la Virgen parecen esculturas que se escapan de la hornacina (Figura 2C). Otra, el espejo de El matrimonio Arnolfini, con permiso de Velázquez, el más famoso de la historia del arte (Figura 2D).
 Imagen 2. A) Virgen del Canciller Rolin (66×62 cm) y B) detalle C) Díptico de la Anunciación (aprox. 39 x 24 cm cada imagen) D) Espejo de El matrimonio Arnolfini. Fuente: http://closertovaneyck.kikirpa.be, © KIK-IRPA, Brussels.
Imagen 2. A) Virgen del Canciller Rolin (66×62 cm) y B) detalle C) Díptico de la Anunciación (aprox. 39 x 24 cm cada imagen) D) Espejo de El matrimonio Arnolfini. Fuente: http://closertovaneyck.kikirpa.be, © KIK-IRPA, Brussels.
A estas alturas espero haberles convencido (si no lo estaban ya) de la importancia que ha tenido van Eyck en la historia del arte. No cabe duda de que su obra merecía ser estudiada empleando los mejores instrumentos a nuestro alcance. Bienvenidos al proyecto VERONA.
El Proyecto VERONA: Van Eyck Research in OpeN Access
La producción artística de Jan van Eyck fue muy reducida, por lo menos teniendo en cuenta las pinturas que se conservan. Hasta tal punto que sólo existen nueve cuadros que lleven su firma. A lo largo del s. XX los historiadores del arte estudiaron con detalle estas obras y, con menor o mayor polémica, llegaron a atribuir una veintena de obras al genio flamenco. Aun sumando las miniaturas del Libro de Horas de Turín-Milán que se le atribuyen a él y a su hermano Hubert, es un legado escaso. Hemos de tener en cuenta que aquellos estudios estilísticos se hicieron en base a unos recursos técnicos limitados, por lo que se antojaba necesario realizar nuevos análisis adaptándose a los tiempos que corren. Así se podría entender mejor el proceso creativo de van Eyck y revisar su creación artística. De eso se encargaron los expertos del Instituto Real del Patrimonio Cultural de Bélgica (KIK-IRPA) quienes, mediante tecnología puntera y siguiendo un protocolo estandarizado, analizaron la obra de Jan van Eyck y la pusieron a disposición no sólo de los expertos, sino del público en general.
En 2014 cargaron una furgoneta con los instrumentos necesarios y viajaron por toda Europa para documentar las pinturas atribuidas a van Eyck que se hallan desperdigadas por diferentes museos (también hay alguna obra en Estados Unidos). En un trayecto de 12 000 kilómetros recogieron 16 298 imágenes para un total de 1 499 gigas de información. Casi nada. Aquí les tenéis estudiando el Díptico de la Anunciación del Museo Thyssen-Bornemisza, por si les queréis ver con las manos en la masa.
 Imagen 3. La instrumentación con la que viajó el equipo del KIK-IRPA. Fuente: http://closertovaneyck.kikirpa.be, © KIK-IRPA, Brussels.
Imagen 3. La instrumentación con la que viajó el equipo del KIK-IRPA. Fuente: http://closertovaneyck.kikirpa.be, © KIK-IRPA, Brussels.
El primer paso del proceso consistía en tomar una fotografía de alta resolución, asegurándose de que se usaban siempre las mismas condiciones para todas las obras. Para ello emplearon una cámara Hasselblad H4D-200MS con un sensor de 50 megapíxeles que, obviamente, no sujetaban a pulso. Se colocaba en un soporte mecánico que se podía desplazar por raíles, lo que permitía realizar macrofotografías (15×20 cm o 7.5×10 cm) que luego se montaban digitalmente para ofrecer imágenes en las que podemos apreciar hasta el más pequeño de los detalles (Imagen 4). Además de tomar las fotografías con iluminación normal, las tomaron con luz rasante y bajo luz ultravioleta, algo que ofrece información complementaria como ya vimos en su momento.
 Imagen 4. Realización de una macrofotografía sobre el Tríptico de Dresden y una ampliación de San Francisco Recibiendo las Agallas a escala milimétrica en la que podemos observar el craquelado de la pintura. Fuente: http://closertovaneyck.kikirpa.be, © KIK-IRPA, Brussels.
Imagen 4. Realización de una macrofotografía sobre el Tríptico de Dresden y una ampliación de San Francisco Recibiendo las Agallas a escala milimétrica en la que podemos observar el craquelado de la pintura. Fuente: http://closertovaneyck.kikirpa.be, © KIK-IRPA, Brussels.
La cámara Hasselblad también estaba equipada para trabajar en el infrarrojo, de modo que se pudiese estudiar el dibujo subyacente de las pinturas. En cualquier caso, para lograr imágenes con una mayor capacidad de penetración se empleó un instrumento de reflectografía infrarroja que permitía trabajar entre los 900 y los 1700 nm. Recordemos que a esas longitudes de onda muchos de los pigmentos no absorben prácticamente energía, mientras que el carbono, tradicionalmente empleado en el dibujo preparatorio, sí lo hace. Gracias a esta técnica se puede conocer mejor el modus operandi de un pintor y ver los cambios realizados a lo largo del proceso de creación. Precisamente uno de los casos paradigmáticos del empleo de la luz infrarroja es El Matrimonio Arnolfini, en cuyo reflectograma se pueden observar los numerosos cambios realizados por van Eyck. Pero quedémonos aquí con un ejemplo que he encontrado trasteando en la web del proyecto VERONA: ¿No os parece que tanto el Niño como la Madre en La Virgen del Canciller Rolin iban a tener los brazos en otra posición?
 Imagen 5. Reflectografía infrarroja del Niño de La Virgen del Canciller Rolin en la que se aprecia el cambio de composición respecto al resultado final. Fuente: http://closertovaneyck.kikirpa.be, © KIK-IRPA, Brussels.
Imagen 5. Reflectografía infrarroja del Niño de La Virgen del Canciller Rolin en la que se aprecia el cambio de composición respecto al resultado final. Fuente: http://closertovaneyck.kikirpa.be, © KIK-IRPA, Brussels.
Siguiendo con la idea de penetrar en la pintura, no se podía dejar de lado el uso de la radiografía. Como la materia absorbe los rayos X en función de los átomos que la componen y la densidad del material, podemos lograr información valiosísima sobre el uso de pigmentos y el estado de la obra. El equipo belga realizó las radiografías mediante instrumentos de rayos X portátiles empleando películas para radiografías (30 x 40 cm) que luego montaron digitalmente. Aquí hemos de decir que el protocolo no está tan estandarizado y que en muchos casos emplearon radiografías realizadas con anterioridad, algo perfectamente comprensible teniendo en cuenta que se trata de una técnica más compleja que las anteriores. Para que os hagáis una idea del tipo de información que se obtiene, os traigo como ejemplo el retrato de Margaret, la mujer del artista (otra de las cosas en las que van Eyck fue un innovador, ya que no era nada habitual este tipo de retratos). Si observáis la Imagen 6, veréis que el tocado ofrece un color claro en la radiografía. Es muy posible que el pintor emplease albayalde, un pigmento blanco que tiene plomo y que por lo tanto absorbe los rayos X.
 Imagen 6. Radiografía de El Retrato de Margaret van Eyck (41×34 cm). Fuente: http://closertovaneyck.kikirpa.be, © KIK-IRPA, Brussels.
Imagen 6. Radiografía de El Retrato de Margaret van Eyck (41×34 cm). Fuente: http://closertovaneyck.kikirpa.be, © KIK-IRPA, Brussels.
Acabemos este recorrido por los estudios técnicos subrayando que, en algunas de las obras, también se han aplicado análisis más específicos sobre pigmentos gracias al uso de la fluorescencia de rayos X. De momento no están disponibles en la página web del proyecto, pero crucemos los dedos para que pronto lo estén. Lo que sí que podemos hacer en dicha web es juguetear con las macrofotografías (Imagen 7), las imágenes en infrarrojo y las radiografías de más de veinte obras obtenidas con la misma escala en una iniciativa que ojalá sólo sea la primera de muchas.
 Imagen 7. Apariencia de la página web del proyecto Verona al comparar cuatro macrofotografías de diferentes vírgenes pintadas por van Eyck. Fuente: http://closertovaneyck.kikirpa.be, © KIK-IRPA, Brussels.
Imagen 7. Apariencia de la página web del proyecto Verona al comparar cuatro macrofotografías de diferentes vírgenes pintadas por van Eyck. Fuente: http://closertovaneyck.kikirpa.be, © KIK-IRPA, Brussels.
La firma
No quería finalizar el artículo sin llamar la atención sobre un aspecto de las pinturas que suele pasar desapercibido: el marco. En las macrofotografías de algunas de las obras podemos observar los marcos originales que todavía se conservan. Ahí es donde en varias ocasiones el artista flamenco dejó su firma, junto al lema AΛΣ IXH XAN (Als Ich Kan). Esta frase vendría a significar “como (mejor) puedo”, toda una fórmula de humildad, aunque también se ha interpretado como un juego de palabras para decir “como van Eyck (sólo) pudo”, lo que tendría un significado bastante diferente. En cualquier caso, no cabe duda de que van Eyck pudo. Vaya si pudo.
 Imagen 8. Marco original de La Virgen de la Fuente con la firma de Jan van Eyck y el lema “AΛΣ IXH XAN” parcialmente visible. Fuente: http://closertovaneyck.kikirpa.be, © KIK-IRPA, Brussels.
Imagen 8. Marco original de La Virgen de la Fuente con la firma de Jan van Eyck y el lema “AΛΣ IXH XAN” parcialmente visible. Fuente: http://closertovaneyck.kikirpa.be, © KIK-IRPA, Brussels.Sobre el autor: Oskar González es profesor en la facultad de Ciencia y Tecnología y en la facultad de Bellas Artes de la UPV/EHU.
El artículo Van Eyck al descubierto se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La tabla periódica en el arte: Cobre
- Descubierto el proceso por el que las bacterias fabrican nanoimanes
- Festín burlesco, una visita al alma del museo
Por qué los biobots no son un problema ético (de momento)
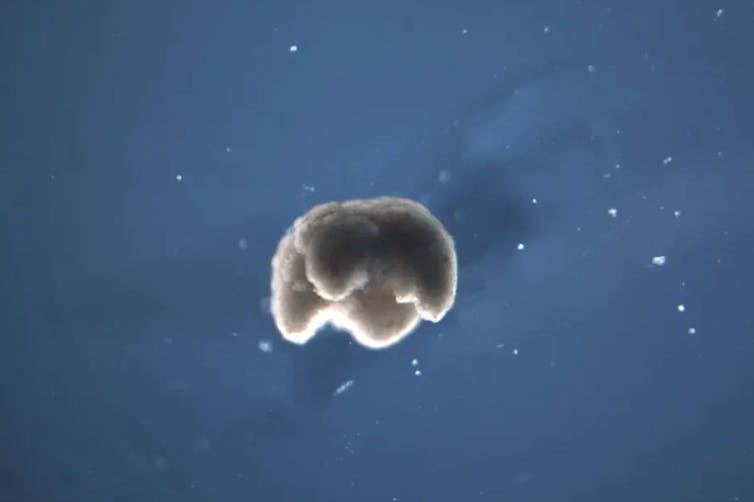 Un organismo 3D diseñado por un algoritmo evolutivo y construido a partir de células vivas.
Un organismo 3D diseñado por un algoritmo evolutivo y construido a partir de células vivas.Douglas Blackiston, CC BY-SA
El pasado 13 de enero se publicó un avance científico que tiene todas las papeletas para convertirse en un hito en la historia de la investigación biotecnológica. Un equipo de cuatro investigadores estadounidenses ha creado un sistema orgánico funcional novedoso, una forma de vida diferente a todas las que existían, algo que jamás se había conseguido antes.
El proceso para llegar a este resultado fue extremadamente arduo. Para empezar, hubo que utilizar un algoritmo evolutivo complejo alojado en un superordenador. Este mecanismo fue el que determinó qué tipo de material biológico – y con qué estructura – habría de emplearse para lograr el objetivo perseguido. A partir de los resultados proporcionados por esa herramienta, se decidió utilizar células procedentes de la piel y el corazón de embriones de ranas africanas, que se moldearon de la forma diseñada por la inteligencia artificial.
La entidad resultante fue una estructura biológica de un milímetro de anchura que se comportaba de manera coordinada en circunstancias hasta ahora esquivas a la acción humana. De hecho, pueden trabajar conjuntamente y sobrevivir incluso semanas sin necesidad de alimento.
Sus posibles aplicaciones incluyen gestionar la contaminación radioactiva, recolectar microplásticos en los océanos e incluso inocular un medicamento en un tumor. Además, estas entidades tienen la ventaja de ser biodegradables, por lo que, en principio, desaparecerían sin dejar rastro una vez cumplido su cometido.
¿Xenobots o biobots?
Nos encontramos ante un descubrimiento de primer orden, que abre las puertas de un mundo desconocido y lleno de promesas, pero tan novedoso que también encierra múltiples interrogantes. Para empezar, ni siquiera está claro cómo tendríamos que denominar a estas criaturas.
En las primeras informaciones facilitadas se ha propuesto el nombre de “Xenobots”, que combina su origen (la denominación científica de las ranas africanas es Xenopus laevis) con el tipo de entidad de la que se trata -– “bots” o robots –.
A mi juicio esta terminología resulta un tanto equívoca, porque la palabra “xeno” significa en griego “extranjero” o “extraño”. Me parece poco afortunado introducir este concepto, que normalmente asociamos a pensamientos negativos, en una nueva tecnología.
Tiene más sentido elegir la denominación de “biobots”, que une a la idea de robotsla de bios, un prefijo que muestra ostensiblemente su carácter de materia viva. Una característica, por cierto, esencial en este caso, ya que es la que dota a las nuevas criaturas tanto de gran plasticidad como de una capacidad a la que suelen ser ajenas las estructuras sintéticas: la de regenerarse a sí mismas en caso de sufrir daño.
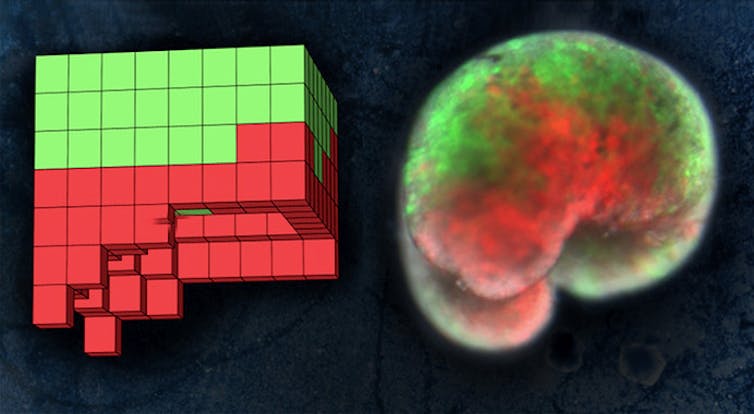 A la izquierda, el plano anatómico de un organismo diseñado por ordenador. A la derecha, el organismo vivo, construido a partir de piel de rana (verde) y células del músculo cardíaco (rojo).
A la izquierda, el plano anatómico de un organismo diseñado por ordenador. A la derecha, el organismo vivo, construido a partir de piel de rana (verde) y células del músculo cardíaco (rojo).Sam Kriegman (UVM), CC BY
Los miedos mitológicos no son razonables
Las cuestiones que se entrelazan con la ética requieren un análisis más profundo. Es fácil presuponer que habrá voces que clamen contra los biobots, ya sea porque nos exponen a escalofriantes peligros aún por determinar o porque su creación atenta por sí misma contra la naturaleza.
La fortaleza de estos argumentos proviene de que conectan muy bien con el imaginario colectivo. Al fin y al cabo, tanto la mitología antigua como la ciencia ficción contemporánea se han encargado de infundirnos un considerable temor a todo lo que parece poco natural. Lo han hecho a través de ejemplos de consecuencias que trae la ambición humana cuando se aúpa a un papel hacedor que no le corresponde.
Contamos con visiones muy pesimistas de lo que la biotecnología puede desencadenar sobre la especie humana. Los ejemplos van desde el mito de quimera, que hizo que los romanos exigiesen forma humana a los recién nacidos para considerarlos personas, hasta relatos como los de La isla del doctor Moreau y películas como GATTACA. Hay toda una herencia de miedo a lo artificial, a lo hecho por el ser humano, entre la que es difícil abrir camino a lo razonable.
La realidad se encuentra, al menos en lo que se refiere a los biobots, muy lejos de parecerse a esos escenarios dantescos.
A diferencia de lo que ocurre con otras tecnologías como la edición genética, las quimeras humano-animales y los organoides, en este caso estamos muy lejos de utilizar material humano, al menos de momento.
Aunque algún día llegáramos al punto de usar células embrionarias humanas para constituir estas estructuras vivas seguiríamos sin poder hablar de seres dotados de valor moral (dignidad). Esta frontera solo se avistará si empezamos a introducir estructuras neuronales en estos biobots.
Este escenario está muy lejos, si es que es viable algún día. Por tanto, solo aquellos que defienden la necesidad de valorar todas y cada una de las formas de vida – una línea de pensamiento minoritaria – podrían preocuparse por la aparición de estas nuevas entidades.
¿Sufren los biobots?
Ahora bien, ¿no debería preocuparnos un cambio tan radical en la estructura de la vida, aunque no afecte al material biológico humano? A mi juicio es obvio que no, aunque entiendo la raíz última de estas inquietudes.
Nuestra visión de la naturaleza tiende a idealizarla. Hablamos de la madre naturaleza y su sabiduría innata, algo panteístico. El sistema que nos rodea no posee atributos como la bondad y la inteligencia. Ciertamente, el mundo físico tiene un orden (variable) y unas normas, una forma de organización. No hay nada, sin embargo, que certifique que ese orden sea el óptimo para nosotros. De hecho, llevamos milenios pensando lo contrario, de ahí las alternaciones de la naturaleza que ha provocado el desarrollo de la medicina, la agricultura y el transporte
Introducir otras, como la creación de biobots,no debería resultar inquietante por sí misma. Otra cosa será inferir si la mera existencia como biobot causa sufrimiento a la criatura creada artificialmente. Este es el punto en el que nos hallamos en el caso de los organoides cerebrales, pero cuesta pensar que las dudas sean extrapolables a entidades que carecen de un centro de interpretación de señales nerviosas.
Si en el futuro nos encontramos ante una situación más compleja, será el momento de retomar esta discusión. Por ahora parece superflua.
Sin riesgos (de momento)
Esto no significa que debamos permitir cualquier uso de esta tecnología. La liberación de organismos de este tipo en un entorno no controlado podría entrañar graves riesgos para el ecosistema.
Tampoco parece posible autorizar, en un futuro próximo, experimentos que impliquen su introducción en el cuerpo de seres vivos, sean o no humanos, por razones de seguridad.
Para evitar estos excesos se encuentra ya en vigor toda una normativa que nos protege de usos poco razonables de tecnologías experimentales. Toda una pléyade de organismos, desde las agencias de seguridad hasta los comités de ética de la investigación, se encargan de vetar iniciativas de dudosa utilidad o elevado riesgo. Al menos, mientras no se hayan recorrido todos los pasos que ha de transitar cualquier tecnología nueva antes de su aplicación práctica.
El derecho también tendrá que estudiar qué estatuto proporciona a estos biobots, o si será necesario desarrollar alguna norma concreta que regule su uso, y seguro que su respuesta será más que satisfactoria.
Mientras tanto, quienes han de aplicar las normas tendrán que intentar hallar en su articulado unas guías generales con las que establecer pautas de acción concretas en este momento preciso. Dudo muchísimo que la aparición de formas de vida como estas suponga un desafío a este respecto.
Cabe pensar que este avance tecnológico merece una mirada esperanzada, aunque sea todavía muy pronto para calibrar su impacto en la práctica. No parece que un uso ordenado de esta tecnología plantee problemas éticos o jurídicos preocupantes. Habrá, en todo caso, que estar muy atentos a sus futuros desarrollos. Ellos nos confirmarán (o no) este primer diagnóstico.![]()
Sobre el autor: Iñigo De Miguel Beriain es Ikerbasque Research Professor e investigador distinguido de la Facultad de Derecho, Universidad del País Vasco / Euskal Herriko Unibertsitatea
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Por qué los biobots no son un problema ético (de momento) se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Pozos de conocimiento: el problema de la profundidad
- El comportamiento corpuscular de la luz: momento lineal del fotón
- Estroncio en la leche
Los retos de geolocalizar a la población española
Rosa Elvira Lillo Rodríguez, Iñaki Úcar y Rubén Cuevas Rumín
 shocky / shutterstock
shocky / shutterstock
La utilización de datos de localización es de vital importancia en episodios de pandemia como estos. Ha demostrado su utilidad en países como Corea del Sur o Singapur. España tiene aspectos diferenciales, especialmente en la cultura, que nos confieren particularidades en la adopción de este tipo de estrategias.
Las aplicaciones: ¿funcionan en España?
El uso de apps es una solución válida. Permiten combinar datos de localización precisa (GPS) con datos de contacto físico en distancias cortas (bluetooth) para trazar de manera bastante precisa los patrones de movilidad así como los encuentros de los ciudadanos (en concreto de aquellos infectados).
La utilización de aplicaciones sirve para desarrollar campañas de confinamiento selectivo en lugar del confinamiento global de la población. Estas han demostrado ser más efectivas en el control de la pandemia (como ha quedado patente en Corea del Sur), a la vez que contribuyen a reducir significativamente su impacto en la economía.
Pero las aplicaciones tienen un problema muy importante en un contexto como el de la sociedad española: hay que conseguir que una gran fracción de la población se la instale y todos los desarrolladores de apps saben que ésta es una tarea muy complicada. Solventar este problema (que no es tecnológico) es crítico para que la solución de la utilización de estas herramientas tenga sentido.
Geolocalizar con datos móviles: falta precisión
En el ámbito de la movilidad, el proyecto que se pretende impulsar es semejante al proyecto piloto que lanzó el INE para complementar el censo.
Los operadores móviles disponen de un gran volumen de datos que, si no se tratan de forma agregada, permiten identificar básicamente a cada ciudadano. Pueden utilizarse para estudiar los patrones de movilidad de las personas y evaluar la eficiencia de las medidas de confinamiento.
Sin embargo, existe una limitación importante respecto a la precisión de la localización. En centros urbanos, una antena puede dar cobertura en un radio de centenares de metros, mientras que en zonas menos pobladas pueden dar cobertura hasta decenas de kilómetros. Esto implica que la precisión del dato de localización no es alta y es especialmente insuficiente en zonas rurales.
Para mejorar la precisión, se necesitan datos con granularidad GPS que ofrecen mucha mayor fiabilidad que los datos de operadoras móviles. Existen proveedores como Google, Facebook y Apple que tienen este tipo de datos a escala global, lo que permite no solo estudiar los patrones de movilidad a nivel de un país sino también a nivel internacional. Esto es extremadamente importante en escenarios de pandemias como el que nos estamos enfrentando.
¿Debemos renunciar a la privacidad?
En cualquiera de los dos escenarios (apps o localización), debemos ser conscientes de que si queremos que se exploten este tipo de datos en una estrategia conjunta de estado, los ciudadanos tenemos que estar dispuestos a que nuestros datos se comparta con alguna institución (por ejemplo, los gobiernos o autoridades sanitarias).
Acotar y amparar jurídicamente la utilización de la información personal es una discusión relevante en el ámbito de la ética. La Agencia Española de Protección de Datos ha indicado criterios adecuados en la utilización de datos masivos. Como ha advertido recientemente, su empleo sería solamente imputable a este momento concreto:
“Esta situación de emergencia no puede suponer una suspensión del derecho fundamental a la protección de datos personales. Pero, al mismo tiempo, la normativa de protección de datos no puede utilizarse para obstaculizar o limitar la efectividad de las medidas que adopten las autoridades competentes”.
Tanto las empresas de telecomunicaciones como las tecnológicas pueden desempeñar un papel fundamental en este escenario. Además de aportar sus datos para que se puedan analizar patrones de movilidad, pueden servir de canal de comunicación con los usuarios.
En comparación con la solución de las apps que necesitan que los ciudadanos se instalen las aplicaciones, estas compañías ya tienen un canal directo de comunicación con decenas de millones de usuarios en un país (el caso de las teleco) y miles de millones en el mundo (en el caso de las grandes tecnológicas).
La utilidad de las iniciativas digitales desarrolladas por el Gobierno es incuestionable, pero también es incuestionable que se tienen que arbitrar medidas para garantizar que se dispone de la información personal mínima indispensable, bajo supuestos bien definidos y relegados a la mejora de la situación de la pandemia. Esta última frase puede parecer utópica, pero debe ser el contexto básico en el que se muevan todos los avances que se llevarán a cabo en los próximos días.![]()
Sobre los autores: Rosa Elvira Lillo Rodríguez es catedrática de estadística e investigación operativa además de directora del IBiDat (Instituto de Big Data Universidad Carlos III-Santander), Iñaki Úcar es investigador postdoctoral en el IBiDat y Rubén Cuevas Rumín, profesor titular y subdirector del IBiDat.
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Los retos de geolocalizar a la población española se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Una población mejor formada es una población más sana
- La delicada situación de la I+D en la economía española, por Javier García y Abel Fernández
- Marcas de agua digitales, qué son y para qué sirven
Me quiere, no me quiere
El amor ha sido el opio de las mujeres, como la religión el de las masas. Mientras nosotras amábamos, los hombres gobernaban
El matemático Steven H. Strogatz es especialista en el estudio de redes complejas y divulgador científico. En 1988 (ver [1]) publicó un artículo en el que proponía modelizar una determinada situación amorosa —entre, por ejemplo, Romeo y Julieta— usando ecuaciones diferenciales.
 Foto: Carlotta Silvestrini / Pixabay
Foto: Carlotta Silvestrini / Pixabay
Tras este artículo, muchas otras personas han escrito sobre este tema, es decir, sobre la modelización matemática de algunas situaciones románticas, intentando prever la evolución en el tiempo de ese vínculo amoroso. Vamos a explicar uno de estos modelos.
Supongamos que R(t) denota el amor de Romeo por Julieta en el tiempo t. Si R(t) tiene valor positivo significa que él la adora, y si es negativo no la soporta demasiado. Del mismo modo, J(t) denota el cariño de Julieta hacia Romeo en el instante t.
Una manera de plantear las ecuaciones que gobiernan la evolución en el tiempo de la relación entre ambos —un posible modelo para esta relación amorosa—es la siguiente:
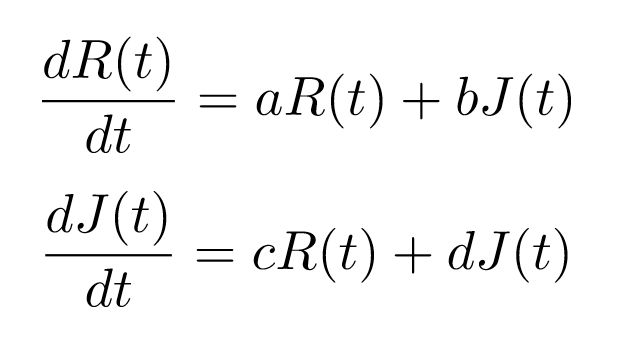
donde las constantes a y b determinan el carácter romántico de Romeo, y c y d la manera de querer de Julieta. Que dR(t)/d(t) sea positivo significa que R(t) aumenta al pasar el tiempo, y sucede lo contrario si es negativo.
¿Qué valores tienen las constantes a, b, c y d? Aunque su valor importa —como veremos más adelante— lo realmente relevante es el signo que poseen cada una de ellas. Que a sea positivo significa que Romeo se siente estimulado por sus propios sentimientos, y que sea negativo denota lo contrario. Si pensamos en b, el que sea positivo expresa que Romeo se siente animado por los sentimientos de Julieta, mientras que un valor negativo significaría que se desanima cuando Julieta siente interés por él. Se puede hacer una interpretación similar de c y d con respecto a la evolución del amor de Julieta por Romeo.
A Strogatz y su alumnado se les ocurrió clasificar los posibles “estilos románticos” del siguiente modo:
-
Si a y b son ambos positivos, hablamos de un castor ansioso: Romeo se siente estimulado tanto por sus propios sentimientos como por los de Julieta.
-
Si a es positivo y b es negativo nos encontramos ante un nerd narcisista: Romeo desea más de lo que siente, pero le asustan los sentimientos de Julieta.
-
Si a es negativo y b es positivo tropezamos con un amante cauteloso: Romeo se retrae ante sus propios sentimientos, pero el cariño que le profesa Julieta lo anima.
-
Si a y b son ambos negativos, nos encontramos con un ermitaño: Romeo huye de sus propios sentimientos y también de los de Julieta.
La manera en el que el amor de Julieta varía con el tiempo se puede clasificar de la misma manera: d se corresponde con a en la ecuación de Romeo, y c con b. Existen diferentes tipos de relaciones dependiendo de los valores de las constantes a, b, c y d. Algunos de ellos se muestran a continuación (pueden encontrarse los detalles en [3], [4] y [5]).
Pasión versus indiferencia
Romeo y Julieta se comportan como “polos opuestos” cuando c=–b y a=-d. las ecuaciones quedan entonces del modo
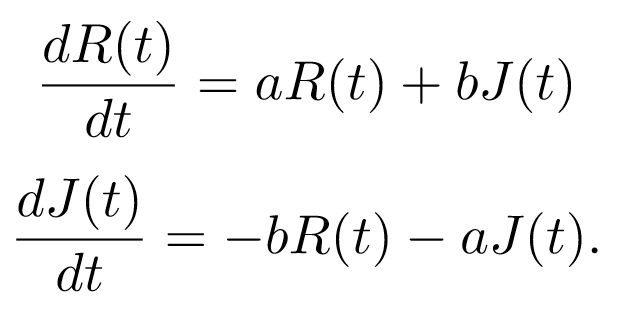
Estas relaciones pueden suceder de dos maneras:
-
Cuando coinciden un castor ansioso y una ermitaña (o viceversa), la evolución en el tiempo de la relación depende de los sentimientos que se priorizan, los propios (|a|>|b|) o los ajenos (|a|). Si Romeo prioriza sus propios sentimientos, la pareja terminará en desacuerdo: uno por siempre enamorado y la otra absolutamente indiferente. Y, en el caso opuesto, la pareja terminará en un ciclo interminable de amor y desamor que sucederán —cada uno de ellos— aproximadamente una cuarta parte del tiempo.
-
Cuando coindicen un nerd narcisista y una amante cautelosa (o viceversa), de nuevo todo depende de la prioridad dada a los sentimientos propios o ajenos. Si |a|>|b|, la pareja finalizará enamorada o en guerra perpetua. Y si |a| terminarán en un eterno ciclo de amor y desamor.
Así que eso de que “polos opuestos” se atraen, no parece que funcione demasiado bien…
Embriagados por los sentimientos ajenos
¿Y si Romeo y Julieta solo se dejan llevar por los sentimientos del otro? Es decir, ¿qué sucede si a=d=0? El sistema de ecuaciones quedaría en este caso del modo siguiente:
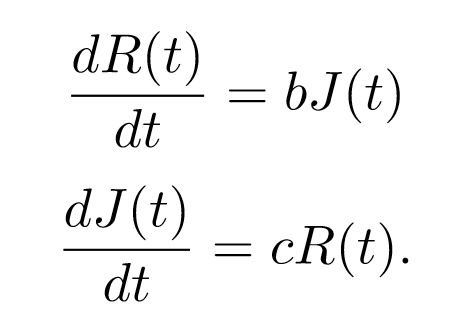
Y tres casos son posibles:
-
Si coinciden dos amantes cautelosos (b>0 y c>0), el resultado es el mismo que el de caso del nerd narcisista y la amante cautelosa con |a|>|b|.
-
Si tenemos dos nerds narcisistas (bccastor ansioso y la ermitaña con |a|>|b|.
-
Y si coinciden un nerd narcisista y una amante cautelosa (o viceversa, es decir, bc
Por cierto, el “modelo de Shakespeare” correspondería al caso en el que a=d=0 y b y c son positivos, es decir, al de dos amantes cautelosos.
Y el modelo de Strogatz —el que propone en [1]— supone que a=d=0, b es negativo y c es positivo, es decir, estudia la relación entre un nerd narcisista y una amante cautelosa. En este caso, Romeo es un amante caprichoso: cuanto más lo quiere Julieta, menos ganas tiene Romeo de cortejarla. Y cuando Julieta pierde el interés por él, Romeo empieza a encontrarla extraordinariamente atractiva. Julieta, por el contrario, se deja llevar por los sentimientos de Romeo: su deseo crece cuando él la adora, y se enfría cuando él la ignora. Como ya sabemos, esta triste historia evoluciona como un interminable ciclo de amor y odio…
¿Cómo evolucionan otros posibles casos? ¿Te atreves a dar un modelo alternativo al planteado arriba?
Referencias
[1] Steven H. Strogatz, Love Affairs and differential equations, Mathematics Magazine 61, 35, 1988
[2] Steven H. Strogatz, Loves Me, Loves Me Not (Do the Math), Opinionator, 2009
[3] Omstavan, Love Affairs: A mathematical model using Differential equations!, Steemit, 2018
[4] Fabian Dablander, Love affairs and linear differential equations, R-bloggers, 2019
[5] Isaac Elishakoff, Differential Equations of Love and Love of Differential Equations, Journal of Humanistic Mathematics 9 (2), 2019, 226-246
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad.
El artículo Me quiere, no me quiere se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Amelia quiere explorar el desierto
- La ‘reverosis’ de Pablo
- La cuadratura del cuadrado: las redes eléctricas de Kirchhoff
Las bandas de Bloch
 Foto: Harli Marten / Unsplash
Foto: Harli Marten / UnsplashEn 1928, solo dos años después de la formulación de la mecánica cuántica, Arnold Sommerfeld modificó el modelo clásico de electrones libres tratando los electrones de acuerdo con la mecánica cuántica. Pero, como antes, Sommerfeld también consideró que los electrones eran pequeñas partículas de materia cargadas. No solo eso, el nuevo modelo aún contenía la suposición poco realista de que los electrones no interactúan con los iones [1] de la red, excepto para colisionar con ellos.
Ese mismo año, Felix Bloch, asistente de Werner Heisenberg en Leipzig, comenzó a hacer suposiciones más razonables en un intento de formular una mecánica cuántica más completa que explicase la conductividad eléctrica.
Primero, Bloch quería asignar un momento y energía definidos a cada uno de los electrones, pero no una posición definida o un intervalo de tiempo, por lo que eligió la faceta de onda de la dualidad onda-corpúsculo [2]. Supuso que los electrones se comportan, no como partículas, sino como ondas de de Broglie infinitamente extensas.
Por lo tanto Bloch no consideraba los electrones dentro de los conductores como un «gas» de partículas, sino más bien como ondas periódicas que se extienden por toda la red cristalina periódica. Este hecho tuvo posteriormente la consecuencia de que permite explicar cómo es que la electricidad puede comenzar a “fluir” por un cable en el mismo instante en que el cable se conecta a una toma de corriente [3].
Bloch hizo una segunda suposición. Supuso que los iones metálicos positivos, que están dispuestos en una matriz periódica infinita (esto es, en un cristal perfecto), ejercen una fuerza eléctrica atractiva sobre los electrones negativos. Esta fuerza atractiva podemos visualizarla como sumideros en el camino de los electrones, técnicamente «pozos de potencial». Los pozos de iones vecinos se superponen de manera que juntos forman una disposición periódica de “baches” que da a las ondas de electrones un recorrido muy irregular por el cable.
Con estas dos suposiciones, Bloch resolvió la ecuación de Schrödinger para averiguar las energías que las de ondas de Broglie de este tipo [4] podrían poseer mientras se movían en este tipo de potencial periódico. Descubrió que las energías permitidas de los electrones en el material se unen en bandas de estados cuánticos, de una forma análoga a como hay ciertos estados estacionarios cuánticos dentro de cada átomo en el que pueden estar los electrones. Entre las bandas, como entre los estados cuánticos, hay un rango de energías en el que los electrones tienen prohibido estar.
Notas:
[1] Un ion tiene carga positiva. Asumir que un electrón cargado negativamente solo interactúa de forma mecánica con ellos es llevar el vacaesferismo hasta casi lo ridículo.
[2] Recordemos esa parte del principio de complementariedad que dice “Cada experimento, o el experimentador que diseña el experimento, selecciona una u otra descripción como la descripción adecuada para ese experimento.”
[3] Démonos cuenta de que, si los electrones se consideran bolitas de materia, la corriente debería emplear un tiempo en llegar a los valores que establece la ley de Ohm.
[4] Recordemos que la ecuación de Schrödinger es una ecuación diferencial y que su solución es, por tanto, una o varias funciones matemáticas llamadas funciones de onda.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Las bandas de Bloch se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La teoría de bandas de los sólidos se hace topológica
- Construyendo la mecánica cuántica
- El principio de complementariedad
Normas de prudencia en el quehacer científico
 Foto: Comfreak / Pixabay
Foto: Comfreak / PixabayDados los dilemas vistos en la anotación anterior y otros que no se han recogido aquí, no dejan de hacerse llamadas de atención, tanto desde la propia comunidad científica, como desde fuera de ella, advirtiendo de la necesidad de actuar con prudencia y en algún caso, de establecer moratorias al uso de ciertas tecnologías hasta no tener maás garantías acerca de su inocuidad.
Con carácter general, y en el marco de su tesis doctoral sobre el entramado de ciencia y valores, Menéndez Viso (2005) propone recuperar la noción aristotélica de prudencia (phronesis) para relacionar lo que sabemos y lo que debe hacerse. Propone que la prudencia inspire las decisiones que toman los científicos y quienes hayan de aplicar los productos de la ciencia.
En este terreno, ya desde los años setenta del siglo pasado se ha propuesto la aplicación del llamado Principio de Precaución a la hora de tomar decisiones relativas a la aplicación de las técnicas objeto de controversia.
El Principio de Precaución empezó a tener reconocimiento jurídico de orden internacional cuando la Asamblea General de Naciones Unidas adoptó la Carta Mundial de la Naturaleza. El Protocolo de Montreal lo incorporó en su formulación en 1987. Y a partir de ese momento tuvo acogida en diferentes tratados internacionales (Declaración de Río y Protocolo de Kioto). También se ha ido incorporando a diferentes legislaciones nacionales.
El Principio de Precaución se sustenta en dos ideas principales:
- La necesidad de que quien toma las decisiones anticipen el daño que puede causar una actuación antes de que ocurra. Esta idea lleva implícito el cambio de la carga de la prueba, porque es quien propone la actuación quien ha de demostrar que no causará daño o que es muy improbable que lo cause.
- La proporcionalidad entre el riesgo y los costes y viabilidad de la acción propuesta
El problema de este principio es que hay numerosas y muy diversas formulaciones del mismo, lo que es indicativo de la dificultad real para objetivar y acordar una definición. A pesar de ello, ha tenido reflejo en el Tratado de Funcionamiento de la Unión Europea y en la legislación de algunos de sus estados. El Consejo de Europa lo define así:
Cuando una evaluación pluridisciplinaria, contradictoria, independiente y transparente, realizada sobre la base de datos disponibles, no permite concluir con certeza sobre un cierto nivel de riesgo, entonces las medidas de gestión del riesgo deben ser tomadas sobre la base de una apreciación política que determine el nivel de protección buscado.
El problema es que es una definición ambigua. La expresión “cierto nivel de riesgo” -que puede tener consecuencias de muy largo alcance- no puede ser más indefinida. Dado que también señala que las medidas han de tomarse “sobre la base de una apreciación política”, en última instancia han de ser criterios de carácter político los que se utilicen a la hora de tomar las decisiones que corresponda.
Y de acuerdo con la fórmula recogida en la web del Parlamento Europeo, este principio habilita a quienes han de tomar decisiones para adoptar medidas de precaución tempranas cuando las pruebas científicas acerca de un peligro para el ambiente o para la salud humana son inciertas y el riesgo es alto.
Holm y Stokes (2012) reconocen la existencia de ese déficit de definición, lo que genera un amplio margen para su aplicación. En sus formulaciones más exigentes el Principio de Precaución es incoherente con la ciencia de la evaluación de riesgos, socava el valor del conocimiento experto y establece objetivos de riesgo 0 nada realistas. También se ha argumentado que es irracional, puesto que su aplicación llega a impedir que se realicen las investigaciones necesarias para establecer los riesgos de forma científica. Otros hemos criticado sus formulaciones más exigentes por la inversión de la carga de la prueba que conlleva, recuperando a estos efectos la filosofía de la llamada prueba diabólica.
Para quienes se oponen al Principio de Precaución, la ambigüedad en su formulación abre un boquete para la toma arbitraria de decisiones. Sus defensores, sin embargo, sostienen que esa ambigüedad es positiva, porque promueve la flexibilidad y la responsabilidad.
Una de las críticas más sólidas que se ha hecho al Principio de Precaución es que su aplicación puede generar costes de oportunidad que acaben causando un daño muy superior al que se pretendía evitar. De hecho, y dado que exige que la carga de la prueba recaiga sobre quien se propone desarrollar o implantar algo nuevo, y no sobre quien trata de impedirlo, sesga la toma de decisiones contra la implantación de nuevas tecnologías. Invenciones y desarrollos tecnológicos como los automóviles, por ejemplo, no habrían quizás superado la prueba de acuerdo con la definición del Consejo de Europa.
Algunos creen que, teniendo en cuenta la magnitud de los beneficios que han reportado las invenciones, la ciencia, la tecnología, en suma, la cultura, a la humanidad, la cautela también podría aplicarse en un sentido diferente. Sostienen que quizás no debería ir dirigida a limitar de forma severa el desarrollo de lo nuevo, sino que debería utilizarse de forma mucho más equilibrada. Al fin y al cabo, la posibilidad de resolver los problemas que la humanidad deba afrontar sólo dependerá de saber cómo hacerlo. Nuestras principales limitaciones son las que se derivan de la ignorancia. Por eso, creen que limitar las posibilidades de irle ganando terreno a la ignorancia puede tener efectos muy negativos.
No son dilemas fáciles. Basta recordar la tragedia de la talidomida, o los efectos del amianto, graves problemas de salud que podían haberse evitado si se hubiese sido más cauteloso en determinadas ocasiones. Pero ello no obsta para tener presente que la cautela debe tener también doble filo: además de para limitar o prohibir, también podría aplicarse para desarrollar y permitir. La evaluación de las novedades debe, por ello, ser lo más equilibrada posible, contemplando riesgos y beneficios, y tratando de evitar que la carga de la prueba recaiga siempre en quien propone alguna innovación.
Hay quien ha formalizado estas cuestiones y les ha dado un tratamiento teórico. De ahí ha surgido lo que denominan el principio de proacción. Esta idea, propuesta por el transhumanista Max More, consiste en una especie de reverso del principio de precaución y consiste en “asumir los riesgos de acuerdo con la ciencia disponible y no la percepción popular” y tener en cuenta no solo los impactos de una tecnología sino los beneficios que se pierden en el caso de no ponerla en marcha.
Para concluir, nos ha parecido de interés traer aquí la idea formulada de manera reciente por la matemática Hannah Fry, quien propone que quienes trabajan en matemáticas, ingeniería informática, ciencia y tecnología deberían hacer una especie de juramento hipocrático, en virtud del cual se comprometerían a pensar de forma rigurosa acerca de las posibles aplicaciones de su trabajo, y obligarse a sí mismos a desarrollar aquellas acerca de las cuales tengan suficientes garantías de que no serán perjudiciales para la sociedad. No es la primera iniciativa en ese sentido (aquí y aquí otras), pero es reciente y está formulada de acuerdo con un procedimiento ya utilizado en el campo de la medicina.
Nada de esto es fácil.
Fuentes:
Holm, S, Stokes E (2012): Precautionary Principle, in Encyclopedia of Applied Ethics, Vol III, pp.: 569-575, 2nd edition, Academic Press, London
Menéndez Viso, A (2005): Las ciencias y el origen de los valores. Siglo XXI.
Este artículo se publicó originalmente en el blog de Jakiunde. Artículo original.
Sobre los autores: Juan Ignacio Perez Iglesias es Director de la Cátedra de Cultura Científica de la UPV/EHU y Joaquín Sevilla Moroder es Director de Cultura y Divulgación de la UPNA.
El artículo Normas de prudencia en el quehacer científico se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El papel de los gobiernos en el desarrollo científico
- El ethos de la ciencia y las normas de Merton
- #Naukas16 ¿Por qué vuela un avión? (y el método científico)
Sí con mis impuestos
 Foto: alobenda / Pixabay
Foto: alobenda / Pixabay
Ignacio López Goñi, catedrático de microbiología de la Universidad de Navarra, ha preguntado en Twitter lo siguiente:
R5 #CitSCiChatES #CienciaCiudadana
Si hace unos meses te hubieran preguntado: Con el dinero de tus impuestos, ¿subvencionarías una investigación sobre virus en murciélagos? ¿Qué habrías respondido?
— microBIO (@microBIOblog) April 8, 2020
Los murciélagos se encuentran entre los animales que más fácilmente pueden estar en el origen de una zoonosis, una enfermedad infecciosa que pasa de forma natural de una especie a otra. Por eso, el conocimiento de su biología y, con más razón, de los virus que pueden transmitirse a los seres humanos, es muy útil, no ya para hacer frente a una pandemia que ha matado a miles de personas y paralizado gran parte del mundo, sino para prevenir futuras pandemias. Pero hay otras disciplinas cuyo conocimiento puede ser crucial para controlar la expansión del virus y evitar el daño que provoca. La virología es un ejemplo evidente. Pero hay más.
Conocemos los linajes en que se ha diversificado el SARS-CoV-2 desde su primer salto a un ser humano gracias a la genética molecular. Sus métodos permitirán, eventualmente, caracterizar las variedades que vayan apareciendo y ayudarán a identificar rasgos peligrosos.
La epidemiología se basa en modelos matemáticos mediante los que trazar el curso de la pandemia y su posible evolución futura. Los modelos se alimentan de datos relativos al número de personas que hay contagiadas en cada momento y de las que han superado la infección. Se sabe quiénes están contagiados gracias a técnicas como la PCR (“reacción en cadena de la polimerasa”), que son el resultado de decenas de años de avances en biología molecular. Y para saber quiénes han estado infectados por el virus se hacen análisis (serológicos) que permiten detectar la presencia de anticuerpos específicos del SARS-CoV-2 en el suero sanguíneo y son fruto de años de trabajo en inmunología y analítica.
La búsqueda de fármacos antivirales se sirve ahora de las técnicas de biología estructural desarrolladas en las últimas décadas. Ya han obtenido imágenes de algunas proteínas del virus con una resolución de unos pocos nanómetros; así han caracterizado, por ejemplo, la estructura de una glucoproteína que sirve al virus para acoplarse a la célula pulmonar y pasar a su interior. Esas imágenes pueden ser cruciales para encontrar una molécula que bloquee esa vía de entrada. Se han obtenido mediante criomicroscopía electrónica, una técnica para cuyo desarrollo ha sido necesario tener un conocimiento muy preciso de la interacción entre las estructuras que se quieren caracterizar y los electrones con que se bombardean. La informática también es esencial, pues sin ella no podría procesarse la información que proporciona el microscopio electrónico.
Al ámbito de la inmunología corresponde el posible desarrollo de anticuerpos específicos contra el virus. Y también el modo de minimizar respuestas inmunitarias exageradas, que pueden deteriorar el epitelio respiratorio y comprometer su funcionalidad.
La obtención de vacunas eficaces y seguras es otra de las líneas prioritarias de actuación contra el virus. Hacen falta cultivos celulares (biología celular) para hacer los primeros ensayos. Hay que infectar ratones diseñados genéticamente para que sus células pulmonares contengan las proteínas de las que se vale el virus para introducirse y proliferar en su interior. Y si los ensayos son satisfactorios hay que producir las vacunas, proceso que, para inmunizar a millones de personas, tiene que satisfacer condiciones tecnológicas de excepción.
Hasta aquí he glosado, sin ánimo de ser exhaustivo, algunas disciplinas clave en la lucha contra COVID-19. Pues bien, ninguna de ellas se habría podido desarrollar sin contar antes con un conocimiento profundo de materias a cuya investigación muchos no querrían que se destinasen sus impuestos.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Sí con mis impuestos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:El campo magnético terrestre más allá de las películas de catástrofes: el canto magnético de las rocas
Los fósiles, los minerales o las rocas son, entre otras cosas, en lo primero que pensamos al hablar de geología, pero lo cierto es que la física es un ámbito científico que difícilmente se puede desvincular de la geología. Y es que el fundamento físico resulta clave a la hora de explicar algunos procesos geológicos que suceden tanto en el océano como en la superficie terrestre.
Con el fin de poner sobre la mesa la estrecha relación entre la geología y la física, los días 27 y 28 de noviembre de 2019 se celebró la jornada divulgativa “Geología para poetas, miopes y despistados: La Geología también tiene su Física”. El evento tuvo lugar en la Sala Baroja del Bizkaia Aretoa de la UPV/EHU en Bilbao.
La segunda edición de esta iniciativa estuvo organizada por miembros del grupo de investigación de Procesos Hidro-Ambientales (HGI) de la Facultad de Ciencia y Tecnología de la Universidad del País Vasco, en colaboración con el Vicerrectorado del Campus de Bizkaia, el Geoparque de la Costa Vasca y la Cátedra de Cultura Científica de la UPV/EHU.

Últimamente parece que está de moda en las películas de catástrofes que existan alteraciones en el campo magnético de la Tierra. De hecho, el campo magnético de la Tierra cambia en tiempos geológicos, porque el planeta está «vivo», y esos cambios dejan su marca en las rocas. Juan José Villalain, profesor del departamento de física de la Universidad de Burgos nos cuenta que nos dicen.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo El campo magnético terrestre más allá de las películas de catástrofes: el canto magnético de las rocas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¡Leamos poesía astronómica en las rocas!
- Las mareas del pasado leídas en las rocas del presente
- Geología, ver más allá de lo que pisamos
La oreja de oso, una joya del Pirineo que guarda el secreto de la resurrección
José Ignacio García Plazaola y Beatriz Fernández-Marín
 ‘Ramonda myconi’, la única planta resurrección de la península ibérica.
‘Ramonda myconi’, la única planta resurrección de la península ibérica.José Ignacio García Plazaola, Author provided
Según la mitología griega, Orfeo, hijo de Apolo y Calíope, intentó rescatar a su amada Eurídice de la muerte. Aunque él logró escapar del inframundo, ella desapareció para siempre. Lamentablemente, Orfeo también murió: fue asesinado y despedazado por las Ménades.
Producto de la combinación de la mitología clásica con la tradición más reciente, se cuenta que de las gotas de sangre de Orfeo brotó una planta, que guardó el recuerdo de su esencia más pura en la capacidad de volver a la vida después de muerta.
Esta planta se conoce hoy en día como flor de Orfeo (Haberlea rhodopensis) y es una de las cinco especies europeas que se incluyen en la familia de las Gesneriáceas.
Todas ellas se localizan en el sur del continente (montañas de Grecia, Macedonia y Bulgaria) y, como describe la mitología, presentan la sorprendente capacidad de volver aparentemente a la vida después de muertas.
Son lo que se denomina “plantas resurrección”. En todo el mundo hay unas 300 plantas resurrección. La mayoría tienen una distribución tropical y subtropical, con la excepción de las Gesneriáceas europeas.
Una planta tropical perdida en el Pirineo
En el Pirineo, tanto en su vertiente norte como sur, tenemos la suerte de contar con una de estas escasísimas plantas resurrección: la emblemática oreja de oso (Ramonda myconi). Es la única especie con estas características de la península ibérica.
El género Ramonda recibe su nombre en honor al botánico y explorador francés Louis Ramond de Carbonnières que, entre otras hazañas, fue el primero en ascender oficialmente al Monte Perdido.
 ‘Ramonda myconi’.
‘Ramonda myconi’.José Ignacio García Plazaola, Author provided
Además de su singularidad como planta resurrección, R. myconi y el resto de Gesneriáceas europeas tienen otra característica muy especial: son plantas de origen tropical, reliquias de un periodo pasado mucho más cálido que el actual. Por eso son denominadas técnicamente “paleotropicales”.
La observación de su morfología y aspecto nos revelará de inmediato ese carácter tropical y fácilmente las asociaremos a la muy conocida violeta africana (género Saintpaulia), planta ornamental de interior.
Siendo una especie de vocación tropical, resulta sorprendente que haya podido adaptarse con éxito al enfriamiento del clima en Europa, muy especialmente en el adverso entorno del Pirineo. Aunque encuentra su óptimo en barrancos calcáreos a mediana altitud, ha llegado a observarse incluso a casi 2 500 m en el entorno del Parque Nacional de Ordesa.
Dado que es una planta de hojas longevas y perennes, su exitoso desarrollo en la alta montaña implica que estas deben ser capaces de sobrevivir a temperaturas extremadamente bajas, algo especialmente llamativo en una especie paleotropical.
Hemos constatado recientemente que sus hojas soportan temperaturas por debajo de cero, e incluso la formación de hielo en su interior, sin sufrir lesiones irreversibles.
La combinación de su carácter de planta resurrección y su destacable tolerancia al frío extremo la convierte en una de las escasísimas plantas capaces de enfrentarse exitosamente tanto a las bajas temperaturas como a la desecación. ¿Cuál es pues su secreto?
Secarse, congelarse, y no morir en el intento
La respuesta probablemente no es única. Más bien al contrario, es un conjunto de características lo que permite a esta planta convertirse en una campeona de resistencia.
Aunque parezca contraintuitivo, las consecuencias biológicas de desecarse o congelarse son parecidas en esencia. Esto justifica en cierto modo que su preadaptación a la desecación ha sido la clave para su supervivencia en el Pirineo.
Básicamente, la planta evita las lesiones celulares reforzando sus membranas para evitar los daños estructurales y oxidativos. Pero la protección no solo debe actuar a nivel celular. Las hojas al deshidratarse deben plegarse siguiendo un patrón bien definido y ordenado de forma similar a como se produce el cierre de un paraguas.
 Plegamiento de las hojas de la oreja de oso.
Plegamiento de las hojas de la oreja de oso.Beatriz Fernández-Marín, Author provided
De este modo, durante el letargo y aparente muerte, los tejidos se mantienen latentes y sin sufrir daños irreparables. Puede incluso llegar a alcanzarse el denominado estado vítreo, en el que la movilidad de las moléculas es muy reducida. Así, los tejidos pueden mantenerse latentes sin apenas acumular daños durante mucho tiempo.
Cuando el agua vuelve a estar disponible, todo el proceso se revierte y las hojas recuperan en unos pocos días su aspecto más lozano. Este momento, el de la resurrección, es el más delicado. Un error en la precisa secuencia de activación del metabolismo puede resultar fatal para la planta.
 El aspecto de la oreja de oso cambia durante las estaciones.
El aspecto de la oreja de oso cambia durante las estaciones.José Ignacio García Plazaola, Author provided
Hoy en día, las plantas resurrección son objeto de estudio en algunos de los mejores laboratorios de fisiología vegetal del mundo. De su espectacular capacidad de volver a la vida podremos aprender muchas lecciones útiles para conseguir una agricultura más sostenible y segura y para desarrollar plantas casi indestructibles.
Curiosamente, algo así intuyó Salvador Dalí. En 1982 estuvo a punto de morir al intentar deshidratarse. Creía que de este modo podría alcanzar la inmortalidad, pues había observado que los microorganismos secos podían volver a la vida con una gotita de agua.
Quién sabe. Quizás las gotas de sangre de Orfeo nos sirvan para desentrañar los secretos de la vida eterna.![]()
Sobre los autores: José Ignacio García Plazaola es profesor de fisiología Vegetal en la Universidad del País Vasco / Euskal Herriko Unibertsitatea y Beatriz Fernández-Marín es profesora de biología vegetal en la Universidad de La Laguna
Este artículo fue publicado originalmente en The Conversation. Artículo original
El artículo La oreja de oso, una joya del Pirineo que guarda el secreto de la resurrección se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- El aporte de amonio aumenta la producción de sustancias anticancerígenas en el brócoli
- El secreto de Hans
- Epigenética, desigualdad y cambio climático
Aplausos
 Photo: Vlah Dumitru / Unsplash
Photo: Vlah Dumitru / UnsplashLuciano Pavarotti actuó muchas veces en Berlín pero el 24 de febrero de 1988 debió de ser una noche excepcional. Al menos, para unos pocos afortunados berlineses. El tenor italiano había ido a la ciudad para representar El elixir de amor de Donizetti en la Ópera Alemana de Berlín. No queda ningún recuerdo sonoro de la ocasión, ni siquiera una triste grabación clandestina. Pero a juzgar por la reacción del público, Pavarotti debió de tocar techo ese día. Según recogen las crónicas y el registro Guinness de los récords, después de su actuación el cantante tuvo que salir hasta 165 veces a saludar al escenario. Los aplausos se prolongaron durante una hora entera y siete minutos.
No se sabe cuándo empezamos a golpear nuestras manos para mostrar aprobación como colectivo, pero es una conducta extendida en casi todas las culturas humanas. El factor común es el ruido, eso sí, más que la palmada. A menudo es posible producirlo con las manos, pero también con algún objeto o con otras partes del cuerpo. Los romanos, por ejemplo, solían agitar la tela de su toga o chasquear los dedos. En países de habla alemana es común entre los estudiantes universitarios golpear las mesas con los nudillos después de cada lección. En otros contextos es común dar golpes con los pies, como cuando los músicos de una orquesta homenajean a su director.
El aplauso, como la risa, parece ser algo contagioso. En el teatro francés los claques eran aplaudidores profesionales, contratados para batir sus manos (incondicionalmente) al final de los espectáculos. No eran muy distintos al público dirigido que hoy anima los platós de televisión. El contagio de los aplausos, no obstante, tiene también un reverso oscuro. No hay nada más temible durante un concierto orquestal, por ejemplo, que una palmada a destiempo durante un silencio que no constituye una pausa. Invariablemente, otras se sumarán a ella rompiendo con su impaciencia el hilo de la música.
Por lo demás, el bramido de las palmadas suele ser algo caótico. Aunque existe cierto ritmo individual, globalmente están descoordinadas, de manera que el sonido total es un ruido homogéneo. Esto no sucede así siempre ni en todas partes, sin embargo. En algunos países de Europa del Este, es popular un tipo particular de aplauso sincronizado, conocido como vastaps o “aplauso de hierro” en húngaro. Se trata de un fenómeno fascinante porque no existe ningún director que coordine las palmas, ninguna señal aparente que dé comienzo al batir simultáneo. El orden surge espontáneamente de todo el colectivo y se disuelve de la misma manera sin que nada (ningún jefe, ningún individuo en concreto) parezca causarlo.
En 1999 un equipo de físicos decidieron asistir a las salas de conciertos de Rumanía y Hungría para estudiar este fenómeno123. Según explica Steven Strogatz en su maravilloso libro Sync4, “las grabaciones mostraron que las audiencias aplaudían desordenadamente al principio, luego cambiaban espontáneamente a aplausos estruendosos y rítmico, con un tempo más lento, y luego recaían en la cacofonía, alternando hasta seis o siete veces entre el caos y la sincronía”. Su comportamiento era similar al de ciertos osciladores armónicos conectados entre sí, como metrónomos apoyados sobre una misma tabla. Cuando la frecuencia de oscilación es parecida, sus movimientos acaban acoplándose, sin importar el punto de partida, siempre que exista algún tipo de comunicación entre ellos.
De forma parecida, los individuos que baten palmas en un auditorio tiene su propia frecuencia natural de aplaudidor y, además, se comunican entre sí porque pueden oír los aplausos de los demás. “Supongamos que la gente está dando palmas de manera desorganizada pero que todos ellos están intentando sincronizarse” explica Strogatz. Aunque, inicialmente, no puedan oír ninguna señal que seguir, “más tarde —y esto es más bien un misterio— un pulso sobresale solo un poquito, quizás porque unos pocos aplaudidores tienen suerte. Ese pulso empezará a oírse por encima del estruendo desorganizado del resto de la audiencia. Y como todos están intentando aplaudir al unísono, tratarán de acoplarse a ese ritmo”5. Un leve pulso surgido quizás, por pura casualidad, acaba arrastrando consigo a un auditorio entero.
Me pregunto si aquella noche del 24 de febrero de 1988, durante una hora entera (seguramente agotadora) de aplausos, los berlineses acabarían moviéndose a la vez, o si con compartir las agujetas al día siguiente se darían por satisfechos. Curiosamente, aunque Pavarotti ostenta el récord de más llamadas a escena, el aplauso más largo de la historia lo provocó en 2014 el poeta estadounidense Dustin Luke Nelson, durante una performance. Luke invitó a su público a aplaudir durante dos horazas y 32 segundos con el objetivo de aprender a apreciar el acto del aplauso en sí y conseguir formar un grupo más cohesionado.
Últimamente, yo pienso mucho en los aplausos. Sobre todo entre las 19:58 y las las 20:10 de cada día. Pienso que a estas alturas de abril, alguien debería avisar a Guinness y dar el récord de 2014 por superado y me imagino a mi prima, enfermera en uno de tantos hospitales saturados de Madrid, saliendo a saludar 165 veces para recibir el afecto que toda esta comunidad le envía. Ojalá toda experiencia nos sirva para formar un grupo más cohesionado. Quién sabe si con un poco de práctica, acabamos aplaudiendo a la vez.
Referencias:
1Z. Néda., E. Ravasz, Y. Brechet, et al. The sound of many hands clapping. Nature 403, 849–850 (2000)
2Z. Néda, E. Ravasz, T. Vicsek, Y. Brechet, A. L. Barabási. Physics of the rhythmic applause. Phys. Rev. E 61, 6987 (2000)
3Thomson, M., Murphy, K. & Lukeman, R. Groups clapping in unison undergo size-dependent error-induced frequency increase. Sci Rep 8, 808 (2018).
4Steven Strogaz, 2003. Sync, How Order Emerges from Chaos in the Universe, Nature, and Daily Life.
5Josie Glausiusz, 2000. The Mathematics of… Applause
.
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo Aplausos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:
