Cuaderno de Cultura Científica

Foto: vubp / Pixabay

El descubrimiento de que existían varias series radiactivas, cada una de las cuales contiene sustancias aparentemente nuevas, creó un problema grave. En 1910, todavía había algunos espacios vacíos en la tabla periódica de los elementos, pero no había suficientes espacios para las muchas sustancias nuevas que aparentemente pareceían surgir en las desintegraciones. La tabla periódica es una forma de presentar los elementos según sus propiedades químicas y, si no podía incluir los “elementos radiactivos”, tendría que ser revisada, quizás de alguna manera drástica y fundamental. Era un problema no menor.

La clave para la solución del rompecabezas radica en la observación de que algunos de las sustancias que se acababan de descubrir como miembros de una serie radiactiva tienen propiedades químicas idénticas a las de los elementos conocidos, aunque algunas de sus propiedades físicas sí son diferentes.

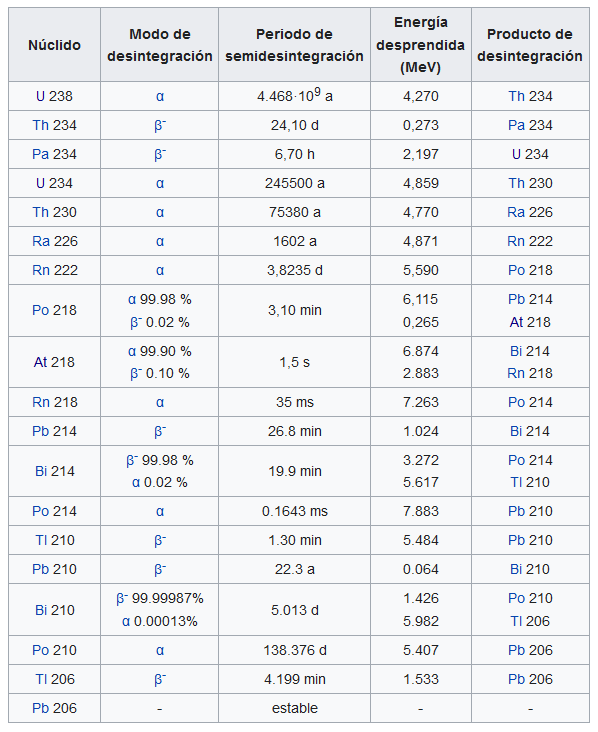Fuente: Wikimedia Commons

Por ejemplo, se descubrió que lo que entonces se llamaba Uranio II, “bisnieto” del Uranio I, tenía las mismas propiedades químicas que el propio Uranio I. Cuando se mezclaban, no se podían separar por medios químicos. Ningún químico ha detectado, mediante análisis químico, ninguna diferencia entre estas dos sustancias [1]. Pero las dos sustancias, ahora conocidas como uranio-238 y uranio-234, difieren entre sí en ciertas propiedades físicas. Como vemos en la tabla, el uranio-238 y el U-234 tienen periodos de semidesintegración bastante diferentes: 4,468·109 años y 2,455·105 años, respectivamente. Si nos fijamos en los modos de desintegración, la masa de un átomo de uranio-234 debe ser menor que la de un átomo de uranio-238 en la masa de una partícula alfa y dos partículas beta.

Otro par de sustancias radiactivas que se descubrieron en la época, llamadas entonces radio B y radio G, tenían las mismas propiedades químicas que el plomo; cuando se mezclan con plomo, no se pueden separar de él por medios químicos. Estas sustancias ahora se conocen como plomo-214 y plomo-206, respectivamente. El plomo 214 es radiactivo y el plomo 206 es estable. La tabla indica que los átomos deben diferir entre sí en masa el equivalente a dos partículas alfa y cinco partículas beta. Hay muchos otros ejemplos de este tipo de diferencias físicas entre dos o más sustancias radiactivas con el mismo comportamiento químico.

Soddy sugirió una solución que cambió nuestra visión sobre la naturaleza de la materia y la relación de los elementos en la tabla periódica. Propuso que un elemento químico podría considerarse como una sustancia pura sólo en el sentido de que todos sus átomos tienen las mismas propiedades químicas; es decir, un elemento químico puede ser en realidad una mezcla de átomos con diferente comportamiento radiactivo y diferentes masas atómicas, pero todos con las mismas propiedades químicas. Había surgido el concepto de isótopo.

Notas:

[1] Otra cosa ocurre en los elementos muy ligeros, donde diferencias pequeñas en términos absolutos son muy importantes en términos relativos. Pero eso fue muy posterior.

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

El artículo Los nuevos ‘elementos’ de las series radiactivas se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Las series de desintegración radiactiva
2. La impureza, por definición, de las muestras radiactivas
3. El modelo de Bohr-Sommerfeld y las propiedades químicas de los elementos

Birgus latro. Ilustración: María Lezana

Birgus latro es el artrópodo terrestre más pesado del mundo. Puede llegar a alcanzar los 4 kg de masa y 40 cm de longitud, aunque sus extremidades extendidas abarcan una distancia de 1m. No es el cangrejo más grande ni, seguramente, tampoco podría ser mayor de lo que es, pues lo más probable es que no pudiera sostener sobre sus extremidades una masa mayor y desplazarse en tierra firme. El más grande es el cangrejo gigante japonés, Macrocheira kaempfrei, pero ese es marino y bajo el agua no operan las restricciones estructurales propias del medio terrestre. Birgus, o cangrejo de los cocoteros, como es conocido, vive en zonas costeras de islas tropicales de los océanos Índico y Pacífico, y se alimenta de cocos, higos, y diversos materiales orgánicos. Su nombre común hace alusión, precisamente, a que consume cocos, lo que no es hazaña pequeña. Los rompe con sus pinzas y come lo que hay en su interior.

Birgus latro no sólo pesa mucho, sino que tiene, además mucha fuerza. En realidad, más que mucha, tiene muchísima fuerza; es el crustáceo que más tiene, de hecho. Hemos sabido de su poderío gracias a un estudio liderado por Shin-Ichiro Oka, de la Okinawa Churasima Foundation, en el que han medido la fuerza que desarrollan 29 cangrejos de los cocoteros de la isla de Okinawa.

Los investigadores observaron que la fuerza que ejercían con sus pinzas era proporcional al tamaño o masa corporal. El valor registrado más alto fue de 1800 newtons (un cangrejo de 2 Kg), por lo que uno de 4 kg llegaría a ejercer una de 3000 newtons. Unas pinzas tan poderosas le permiten consumir una gran variedad de productos, como ya se ha apuntado. Y también son una poderosa arma defensiva, lo que le ayuda a evitar los ataques de buen número de depredadores potenciales y a rechazar la presencia en su entorno de posibles competidores.

Es difícil hacerse una idea de lo que significan 2000 o 3000 newtons. Pongámoslo, pues, en un contexto más amplio. Una langosta ejercería una fuerza de no más de 250 newtons con sus pinzas, muy inferior a la de Birgus. Nuestras manos desarrollan alrededor de 300. Y, en el otro extremo, la mandíbula de un cocodrilo, de unos 16000, la más intensa que es capaz de desarrollar un animal.

Fuente: Shin-ichiro Oka, Taketeru Tomita, Kei Miyamoto (2016): A Mighty Claw: Pinching Force of the Coconut Crab, the Largest Terrestrial Crustacean. PlosOne.

Nota: Esta anotación está basada en Un poderoso crustáceo, de Juan Ignacio Pérez Iglesias, publicada en ZooLogik.

El artículo Las pinzas más poderosas del reino animal se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. La distribución del agua animal y el curioso caso del potasio
2. Evolución del tamaño animal
3. El balance energético animal

Josep Lluís Pelegrí i Llopart

Foto: Romello Williams / Unsplash

Toda una vida de estudio de los océanos me ha regalado la oportunidad de asomarme a su complejidad e inteligencia. Inicialmente me centré en analizar los componentes oceánicos por separado pero con los años descubrí que la belleza y riqueza de los bloques está en su complementariedad, en sus interconexiones, en su rol generador de la complejidad planetaria.

En el 2008 presenté una aproximación fisiológica a los océanos que propone que el sistema de circulación oceánico funciona de forma similar al sistema circulatorio de organismos complejos como los mamíferos. Un sencillo modelo fisiológico explicaba el patrón glacial-interglacial del CO₂ atmosférico.

El modelo fue posteriormente ajustado con algoritmos genéticos, demostrando que la oscilación natural del carbono atmosférico puede deberse a la transformación entre las formas orgánica e inorgánica de carbono disuelto en los océanos.

En términos fisiológicos, el corazón superficial del océano late con periodicidad anual e inicia un sistema circulatorio planetario con dos fases principales:

• Es muy activo en épocas interglaciales, con un metabolismo elevado que transforma grandes cantidades de carbono y nutrientes inorgánicos vía fotosíntesis.
• Se ralentiza durante los periodos glaciales, una fase de reposo con el almacenamiento de materia orgánica disuelta como forma de energía en reserva.

El océano, un ser vivo

Recientemente, bajo la premisa de que océano y atmósfera maximizan el flujo latitudinal de energía, hemos desarrollado un modelo energético planetario.

El modelo reproduce correctamente las tendencias climáticas entre el último máximo glacial y la actualidad, y hace predicciones razonables para finales de siglo. Un corolario de este trabajo es que la Tierra experimenta patrones espaciales que optimizan el flujo de propiedades, similares a los observados en estructuras y especies que han pervivido y evolucionado a lo largo del tiempo.

Estos estudios conceptuales sobre patrones fisiológicos temporales y espaciales, junto con muchos trabajos oceanográficos observacionales y numéricos en diferentes regiones del planeta, permiten reinterpretar la complejidad del planeta océano. Partiendo de un breve recordatorio de la hipótesis Gaia y apelando a la visión de la vida como proceso, reexaminaré el papel fundamental del agua y los océanos en nuestro planeta.

Una nueva mirada a Gaia

Durante la década de los 70, James Lovelock y Lynn Margulis propusieron que la vida interviene en la creación del ambiente planetario. Regula el entorno físico de modo que se optimiza el desarrollo de la propia vida.

Esta propuesta –la teoría Gaia– generó una nueva mirada a nuestro planeta, incluida una notable dosis de controversia, pero no consiguió entusiasmar a gran parte de la comunidad científica debido a la aparente imposibilidad práctica de verificarla.

A pesar de algunos valiosos esfuerzos durante esta última década (Harding, Crist y Rinker, Castro), el enfoque predominante actual sobre nuestro planeta es sistémico, tal como se puede ver por la gran proliferación de libros y revistas científicas sobre el sistema Tierra.

En este momento en que el ideario de Gaia parece haber cedido paso al pragmatismo del big data y las redes inteligentes, sorprende ver cómo muchos programas y organizaciones toman como lema el simbolismo del planeta vivo (p. ej. Living Earth, Living Planet, Living Ocean).

Estos programas surgen de nuestra nueva capacidad de observar con elevada precisión la casi totalidad de la superficie del planeta. Lo que antes era remoto e inaccesible aparece cercano y se transmite la imagen de familiaridad.

Sin embargo, estos programas se centran más en diseccionar los bloques (ambiente físico-químico, individuos y comunidades, ecosistemas) que en comprender el engranaje del todo. Su visión compartimentada de la Tierra dista mucho de la idea holística de un planeta vivo.

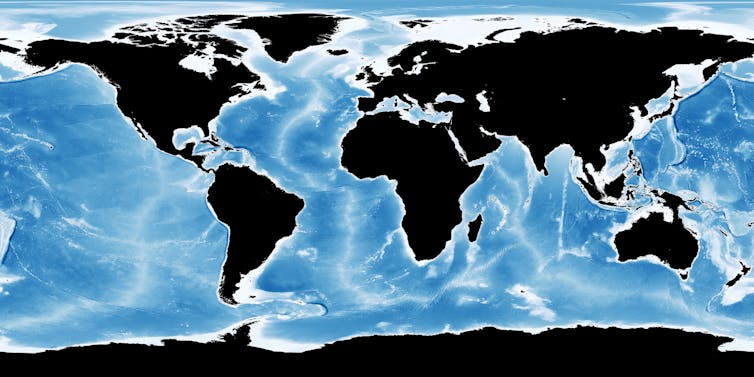Imagen batimétrica de la Tierra.
NASA / Jesse Allen con datos de General Bathymetric Chart of the Oceans (GEBCO) del British Oceanographic Data Centre., CC BY

La vida como proceso

La visión clásica de la vida se basa en la sustancia: el ser vivo material desarrolla funciones complejas, en aparente equilibrio, dentro de unos límites físicos delimitados. Este ser vivo –físicamente diferenciado, conexo y atrapado en un espacio limitado– se organiza y autorregula respondiendo y adaptándose a estímulos externos.

Una visión opuesta de la vida se basa en procesos dinámicos, que mantienen un flujo homeostático de propiedades. Materia, energía e información fluyen creando complementariedad y resiliencia, maximizando la complejidad y minimizando el desorden (entropía).

Desaparece la restricción espacial y temporal del individuo, las entidades diferenciadas se aprecian solo como una imagen estática dentro del flujo continuo de procesos. Temporalmente, algunas regiones exhiben un elevado grado de organización, pero renuevan completamente su materia en ciclos mucho más cortos.

La vida como proceso abre una nueva perspectiva a la hipótesis Gaia. Se puede afirmar con certeza que ninguna parte del sistema Tierra, incluidos los seres humanos, está cerrada. Solo la biosfera, con los océanos como elemento esencial y central, es realmente independiente, un sistema de una complejidad inconmensurable que solo requiere energía solar.

Flujo de vida, flujo de agua

En el flujo de materia, energía e información –el flujo de la vida–, el agua aparece como compuesto químico indispensable. Hace más de un siglo, Lawrence Henderson nos introdujo a sus maravillosas propiedades térmicas y como solvente (de carbono, nutrientes y sales, entre otras). Recientemente, Gerald Pollack ha enfatizado su ocasional comportamiento cristalino, con sorprendentes afinidades espaciales y temporales.

El agua, que conecta los lugares más alejados del planeta como solvente líquido o como soluto, líquido en el subsuelo y gaseoso en la atmósfera, también llega a los espacios más minúsculos donde tienen lugar los procesos moleculares de nuestra existencia.

El flujo del agua entre el medio y las entidades, llámense ecosistemas o individuos, aparece en todas las escalas: desde la formación de los océanos por el impacto de cometas o meteoritos y el reciclado del carbono gracias a la lubricación de las placas tectónicas hasta la transformación de la energía solar en energía química por medio de la fotosíntesis y los ciclos biogeoquímicos responsables del mantenimiento del volumen de agua planetaria.

Imagen de satélite de la Tierra.
Goddard Space Flight Center/NASA

Planeta océano

Hablar del ciclo hidrológico es hablar de océanos, y hablar de océanos es hablar de vida. Los océanos son medio, estructura y propósito: contienen el 97 % del agua de nuestro mundo y son el mayor repositorio de las propiedades vitales para la vida, con más del 95 % de la actividad metabólica planetaria.

Los frentes y corrientes oceánicos establecen el entorno físico y biogeoquímico, caracterizando regiones y definiendo el grado de conexión entre ecosistemas. Como resultado, las diferentes cuencas oceánicas asumen roles fisiológicos complementarios que posibilitan el funcionamiento del organismo planetario.

El océano vivo deja de ser una frase metafórica, se convierte en una realidad formada por mucho más que individuos, comunidades y ecosistemas marinos. Al flujo de materia (agua y propiedades biogeoquímicas) le acompaña el de energía (en todas sus formas, desde interna y mecánica hasta química, almacenada como materia orgánica) e información (genética, ambiente, comunidades). De aquí que la búsqueda de exoplanetas con vida empieza por la identificación de planetas océano.

Salud y consciencia planetaria

Es incuestionable que ninguna entidad en la Tierra, incluidos los humanos, está aislada. Gracias a los océanos, gracias al flujo del agua y sus múltiples propiedades, todos estamos interconectados con nuestro entorno y entre nosotros.

La vida como proceso cuestiona la individualidad: materia, energía e información forman parte del flujo universal, así ha sido durante 3 800 millones de años de vida planetaria. Cada uno de nosotros forma parte del planeta, a pesar de que en cada instante nos manifestamos con un elevado grado de organización en un espacio aparentemente limitado.

El futuro de una humanidad en armonía con su entorno yace en nuestra habilidad para desarrollar una consciencia planetaria. La salud del planeta depende de la salud de cada una de sus partes y viceversa, la salud de todo el organismo planetario es lo que nos traerá salud aquí y ahora.

La pandemia de COVID-19 y la emergencia climática son claros ejemplos de que salud y consciencia planetaria van de la mano.

 

Sobre el autor: Josep Lluís Pelegrí i Llopart es oceanógrafo, profesor de investigación y director del Instituto de Ciencias del Mar (ICM-CSIC)

Este artículo fue publicado originalmente en The Conversation. Artículo original.

El artículo Planeta océano: el corazón líquido que nos mantiene vivos se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Abonar el mar para enfriar el planeta
2. Otra mirada al planeta: arte y geología
3. ¿Qué hay más allá de la orilla del mar?

La semana pasada tuvo lugar la presentación mundial de Ciencia y Misterio, un proyecto de la Universidad Pública de Navarra. Se trata de una webserie con su misterio y su humor que pretende mostrar algunos de los problemas actuales de la actividad científica, como el fraude, la presión por publicar o el exceso de horas de trabajo.

La webserie está compuesta por los 5 capítulos que aparecen abajo. En el último están los créditos de todas las personas que han participado. El acto de presentación en el que guionistas, actores, y el director (con algún invitado ilustre además) comentaron el proyecto puede verse aquí.

Episodio 1

Episodio 2

Episodio 3

Episodio 4

Episodio 5

Edición realizada por César Tomé López

El artículo Ciencia y Misterio, la webserie se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. El misterio de la gelatina de Lorenzini
2. El lenguaje de los libros de alquimia oscura y el misterio de la existencia de éstos
3. El misterio del pez eléctrico monofásico*

Javier Portillo Berasaluce, Arantzazu López de la Serna, y Naiara Bilbao Quintana

Photo by Thomas Park on Unsplash

El 91 % del total de estudiantes del mundo se ha visto afectado por el cierre de los centros de enseñanza en 194 países debido a la pandemia. Este enorme desafío global ha generado una transición abrupta y no planificada a la enseñanza a distancia.

Resulta evidente que no estábamos preparados para una transición tan brusca, pero no lo es menos que la enseñanza a distancia tiene que ser parte de la solución, aunque determinar en qué forma y porcentaje y cómo articularla siguen siendo cuestiones abiertas.

Los retos globales que afrontamos tras la primera oleada son la recuperación a corto plazo y la construcción de sistemas educativos resilientes y equitativos para el futuro.

La respuesta a dichos retos no es una solución “llave en mano”. El “santo grial” de la educación a distancia no es la plataforma tecnológica online de turno, ofrecida ahora en bandeja de plata por multinacionales como Google o Microsoft.

Recortes de la autonomía docente

Ya en los últimos años venían manifestándose inquietudes sobre si el creciente protagonismo de corporaciones privadas internacionales podría recortar la autonomía profesional y los derechos del personal docente, así como el control local de las comunidades sobre sus escuelas.

Los habituales acuerdos asumidos con ligereza entre estas empresas y sus consumidores pueden modificar la concepción de la educación como un bien público. La Internacional de la Educación advierte que el contexto de la pandemia ha servido para que se nos ofrezcan productos tecnológicos para capitalizarlos en un futuro con objetivos comerciales y privatizadores de la educación.

Sobre la vuelta a la escuela en la nueva normalidad, la UNESCO, junto a la OIT (Organización Internacional del Trabajo) han editado un documento dirigido a los responsables políticos con el objeto de guiarles en el apoyo que la pandemia ha demostrado que necesita la comunidad educativa.

Otras necesidades que no son tecnológicas

El mensaje es claro, se requiere invertir en respuestas educativas que incluyan la contratación de más personal; la protección de los derechos y condiciones de trabajo de los docentes; la atención al impacto psicológico y socioemocional de la pandemia en alumnado y profesorado; la capacitación y preparación profesional adecuada para una escuela reconfigurada con impartición presencial y a distancia…

Quizás la COVID-19 haya decantado definitivamente el debate sobre las ventajas de la educación híbrida (Blended Learning), pues la tozuda realidad impone su uso; quizás disminuya la aversión total a las tecnologías de parte del colectivo, porque toda ayuda es necesaria cuando el confinamiento rompe en pedazos el modelo de docencia en el aula; quizás el colectivo más tecnólogo tenga que atenuar su entusiasmo, pues la tecnología per se no ha sido capaz de solucionar la situación de manera totalmente satisfactoria; quizás la regulación legal del trabajo a distancia sea prioritaria, pues deben protegerse los derechos laborales del cuerpo docente y deben prevenirse los efectos perniciosos a largo plazo de determinados usos de plataformas online.

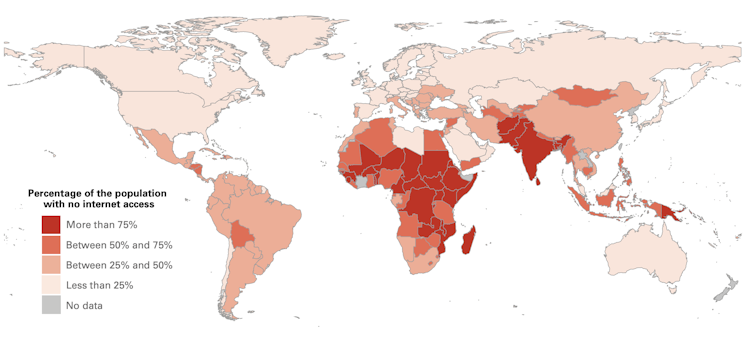La brecha digital: Porcentaje de población sin acceso a internet.
Promising practices for equitable remote learning: Emerging lessons from COVID-19 education responses in 127 countries, UNICEF, Office of Research-Innocenti

826 millones de estudiantes sin ordenador

En Europa Occidental identificamos de forma natural la educación a distancia con el uso combinado de dispositivos electrónicos y conexiones de internet de alta velocidad. La realidad internacional es otra, 826 millones de estudiantes (la mitad) no disponen de un ordenador en casa y 706 millones no tienen acceso a internet.

Esta realidad ha provocado que la respuesta educativa a distancia durante el confinamiento del 68 % de los países haya sido una combinación de: medios digitales (73 %), televisión (75 %), radio (58 %), recursos en papel repartidos a los hogares (48 %) y visitas (7 %).

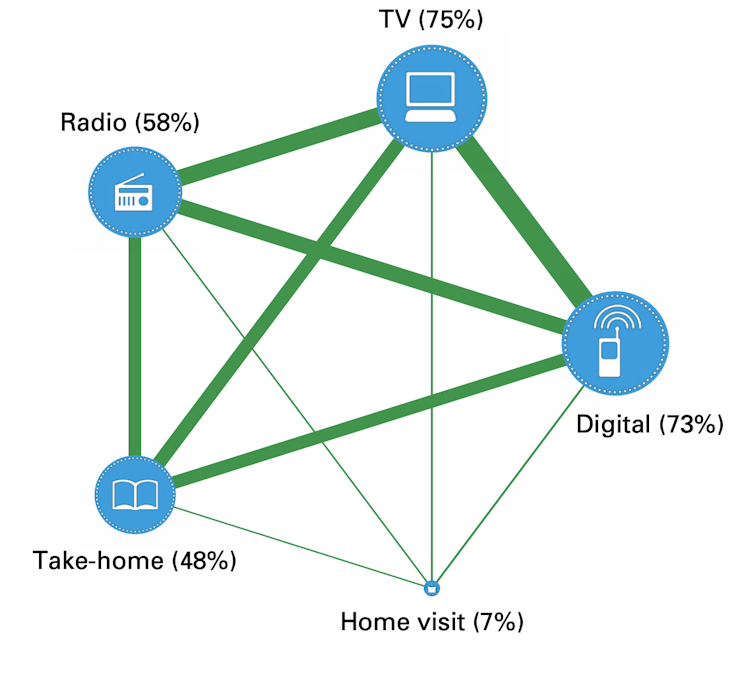Porcentaje de países según el modelo de enseñanza remota.
Promising practices for equitable remote learning: Emerging lessons from COVID-19 education responses in 127 countries, UNICEF, Office of Research-Innocenti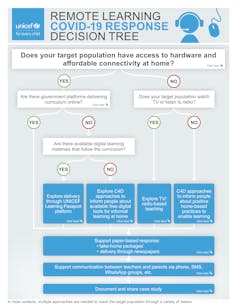Árbol de decisión sobre enseñanza remota.
UNICEF / Red Interagencial para la Educación en Situaciones de Emergencia (INEE)

Asimismo, la esencial realimentación de padres, madres y tutores se ha llevado a cabo mediante SMS, chatbots y aplicaciones de mensajería.

La variedad de contextos es tan amplia –tener o no electricidad, radio, TV, teléfono móvil, conexión de internet u ordenador– que UNICEF ha desarrollado un árbol de decisión sobre enseñanza remota, una herramienta rápida para determinar los canales más apropiados para la distribución de contenidos educativos.

Papel versus tecnología

Es interesante remarcar que, independientemente de la disponibilidad de ordenadores o plataformas online, UNICEF recomienda tener un soporte redundante a la comunicación online a través de papel para la distribución de contenidos y mediante SMS o teléfono para la realimentación entre educadores y tutores.

Esta estrategia permite, por un lado, disponer de un “plan B” para los casos en que fallen recursos que ya tenemos interiorizados como básicos en nuestro día a día como plataformas educativas online o conexión a internet, y por otro lado, asegura un canal de distribución de contenidos educativos para aquellas familias con menor poder adquisitivo que no dispongan de dichos recursos.

Así, tanto el uso de lo que se ha venido a denominar tecnología frugal, como la redundancia en los canales de distribución y comunicación son ingredientes necesarios en un sistema educativo resilente y equitativo.

La inclusión es la clave

La ONU aboga por un cambio generalizado en el mundo del trabajo hacia una digitalización más inclusiva y centrada en las personas.

La educación, concretamente, es una actividad eminentemente social en la que no debería obviarse la importancia del apoyo entre iguales. Esta máxima afecta al colectivo de estudiantes donde el refuerzo de la coevaluación, tutoría y mentoría entre alumnos tiene mucho potencial de crecimiento en situaciones de enseñanza híbrida o a distancia.

Asimismo, una comunidad de profesorado interconectado constituye una red bien tejida que arropa a cada profesional y facilita el debate, compartición de recursos, colaboración, realimentación y evaluación entre iguales. Las instituciones podrían incentivar el fortalecimiento de estas comunidades, tanto nacionales como internacionales, impulsando así el uso compartido de los recursos generados en formato abierto.

En conclusión, la enseñanza a distancia llegó para quedarse, bien como complemento que enriquezca la presencial, bien como recurso más intensivo en situaciones de confinamiento.

Ahora bien, la enseñanza a distancia no puede sustituir quirúrgicamente a la presencial, ni una plataforma online puede sustituir todas las interacciones entre personas que se dan en un aula, ni la necesaria labor del profesor o profesora.

El santo grial de la educación a distancia está en el profesorado. Es prioritario invertir en el capital humano que va a diseñar y modular los procesos de enseñanza-aprendizaje, que se basan en la interacción entre personas.

 

Sobre los autores: Javier Portillo Berasaluce, Arantzazu López de la Serna, y Naiara Bilbao Quintana, son profesores del departamento de Didáctica y Organización Escolar de la Universidad del País Vasco / Euskal Herriko Unibertsitatea

Este artículo fue publicado originalmente en The Conversation. Artículo original.

El artículo ¿Cómo abordar la ‘nueva enseñanza’ si la mitad de los estudiantes no tiene internet ni ordenador? se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. La enseñanza multilingüe de las lenguas
2. Científicos y estudiantes se encuentran a través de Internet
3. El sensacionalismo en las noticias clave en la concienciación sobre los riesgos de Internet

No es fácil atrapar los sonidos musicales en un trozo de papel. La música, con su poder evocativo, su insólita capacidad para agarrarnos de las emociones, parece esquivar cualquier representación sistemática. Una nota flota en el aire, atraviesa una cabeza, llega hasta el estómago y se va. Entre tanto, el estómago se ha arrugado, la cabeza se ha quedado temblando, el humano tiene los pelos de punta. Pero no hay palabras que describan fácilmente esa sensación. No hay referentes externos a la propia música que puedan explicar lo que ha sucedido.

Quizás por eso, hubo un tiempo en el que las melodías solo existían en el aire. Así sigue siendo en la mayoría de culturas del mundo. Luego inventamos la notación musical, un cazamariposas de tinta y papel, que tiene por objetivo congelar esas melodías y hacerlas viajar más lejos, en el espacio y en el tiempo. Los primeros en intentar usarlo fueron los sumerios. Más que escribir la música, ellos registraron la manera de interpretarla. Recurrieron a números que marcaban las distancias entre notas tal y como se interpretaban sobre las cuerdas de un instrumento. De forma parecida, una tablatura contemporánea para guitarra usa también cifras que señalan los trastes donde el intérprete debe colocar sus dedos. Las partituras de la tradición clásica, en cambio, intentan representar los sonidos mismos, con independencia del instrumento con que se toquen. Para ello, usa una rejilla de cinco líneas y cuatro espacios que se corresponden con las notas de una escala, el famoso pentagrama. Sobre él se sitúan distintos tipos de símbolos que representan las duraciones temporales de las notas (el ritmo), su dinámica (cómo de fuerte o suave debe sonar) su timbre o, incluso, el carácter con que deben interpretarse.

En su afán por fijar los sonidos, sin embargo, la mayoría de estos sistemas perdieron flexibilidad para retratar la música. Como las letras de nuestro alfabeto (símbolos abstractos que un día fueron ideogramas, que antes fueron simplemente dibujos) los signos de un pentagrama fueron ganando precisión a base de recurrir a convenciones. Como contrapartida, su significado quedó oculto para todos los extraños a esa convención. Hoy es difícil adivinar, a golpe de ojo, cómo suena la música de una tablatura o de un pentagrama a menos que uno esté entrenado para leerlos. Para el lego, son mensajes cifrados, las huellas de una hormiga errática y muda.

Existen formas menos precisas y, al mismo tiempo, más transparentes de pintar la música. Mi ejemplo parecido, en este sentido, son las partituras de la música budista del Tibet escritas en notación Yang Yig. Resulta hipnótico mirar estos documentos. Siempre acompañando a un texto, una línea se curva sobre el papel, asciende y desciende, se arruga, despega o crece. Parece el dibujo de los sonidos mismos bailando en el aire, la huella imaginaria de una voz.

Tres fragmentos de una partitura tibetana utilizada en un ritual de un monasterio budista. Fuente: Wellcome Collection

 

Cuando veo estos trazos, me acuerdo de Syrinx, un precioso solo para flauta de Claude Debussy. Fue compuesto hacia 1913 como banda sonora para una obra de teatro de Gabriel Mourey. Syrinx era, según el relato al que acompañaba, la última melodía que tocó el dios Pan antes de morir y debía tocarse desde fuera del escenario. Hoy, sin embargo, ocupa un lugar protagonista. A lo largo del siglo XX se fue convirtiendo en una de las composiciones más importantes del repertorio clásico para flauta, una obra que todo intérprete profesional debe conocer y dominar. Su melodía llena de exotismo y sensualidad es la excusa perfecta para jugar con todas las posibilidades del instrumento, con toda su elocuencia y toda su dulzura. Así lo vio también Mourey quien, al escuchar el solo lo describió como «una verdadera joya de sentimiento y emoción contenida, tristeza, belleza plástica y discreta ternura y poesía». Su obra de teatro, curiosamente, nunca llegó a completarse. Hoy solo se la recuerda como excusa: la semilla que dio lugar a una de las obras más bellas para flauta del siglo XX y desapareció.

Muchos historiadores consideran que Syrinx marcó un hito en la historia de la composición precisamente por permitir una libertad de interpretación desconocida hasta la fecha. Durante tres minutos, una flauta de plata dibuja en el aire una melodía llena de destellos. El tiempo se curva a voluntad del flautista, que se convierte en el verdadero centro de toda la obra. Cada compás tiene una duración distinta, cada nota se avalanza sobre la siguiente o se detiene obstinadamente, negándose a avanzar. Incluso el final queda abierto, en forma de signo de interrogación sobre una nota que se apaga (como Pan, quizás). Syrinx es un garabato, una mariposa díscola, el reflejo en el agua de una melodía.

Según una leyenda popular entre músicos, este solo para flauta fue escrito inicialmente por Debussy sin barras de compás ni líneas de respiración. Los manuscritos encontrados muestran que esta historia probablemente no es cierta pero es fácil entender el porqué de su popularidad. La melodía del Syrinx parece una criatura viva: no hay dos sonidos iguales, ni ningún pulso regular que parezca dictar su camino. En ese sentido, recuerda mucho más a los intrincados dibujos de las partituras del Tíbet que a las líneas rectas de un pentagrama. Curiosamente, este sistema de notación oriental no recoge el ritmo ni la duración de las notas. Se ideó como ayuda mnemotécnica para guiar el canto ritual de los monjes hacia el siglo VI, consistente en subidas y caídas suaves de la entonación. La notación recoge estas variaciones mediante curvas, así como instrucciones sobre el carácter con que debe interpretarse la música (fluyendo como un río, ligero como el canto de un pájaro1) y otros detalles sobre los cambios vocales y de entonación. Por lo demás, los cantos Yang son extremadamente graves, muy reiterativos, nada que ver con los destellos de Syrinx. Pero es, sin duda, esa ausencia de paredes temporales, tan infrecuente en la música, lo que los une. Una línea curva que va desde Debussy a un retrato involuntario de su música, dibujado desde en el extremo opuesto del mundo.

Nota:

1The Schoyen Collection. MS 5280/1

Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica

 

El artículo Del Tíbet a Debussy en una partitura se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. El último puzle de Bach
2. Receta de un Adagio (1)
3. Tema y variaciones

 

Hay estudios que afirman que los textos acompañados de muchas fórmulas matemáticas aburren o saturan… y la gente deja de leer. Una lástima, porque las hay realmente hermosas. En este texto va a haber fórmulas trigonométricas –y son preciosas–, pero también otras sorpresas matemáticas. ¡Y además vamos a hacer alguna demostración!

Vamos a ello. Las siguientes fórmulas involucran los coeficientes binomiales para el cálculo del seno, el coseno y la tangente del ángulo nθ en función del seno, el coseno y la tangente del ángulo θ (n es un entero positivo):

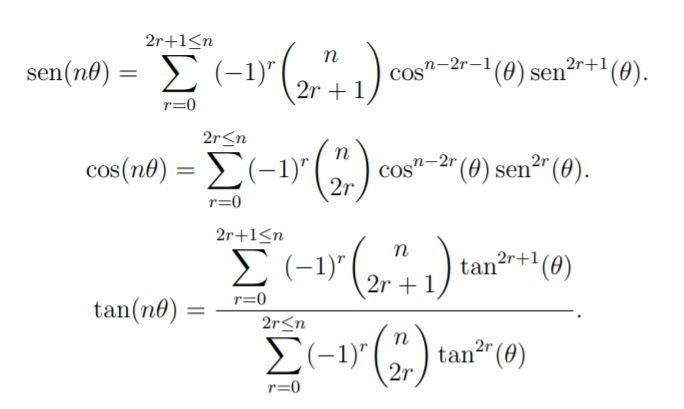
En efecto, la fórmula de De Moivre para números complejos afirma que:

Desarrollando el segundo miembro de la anterior igualdad –usando el teorema del binomio–, queda:

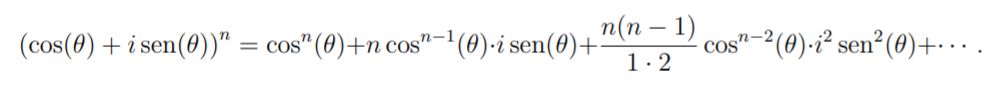
Como la unidad imaginaria verifica que i2=-1, i3=-i, i4=1, i5=i, etc., sustituyendo en la anterior ecuación y agrupando las partes real e imaginaria, obtenemos:

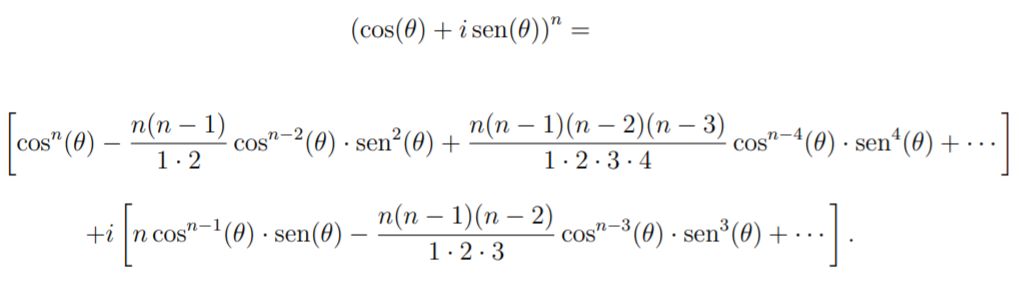
Igualando las partes real e imaginaria, queda:

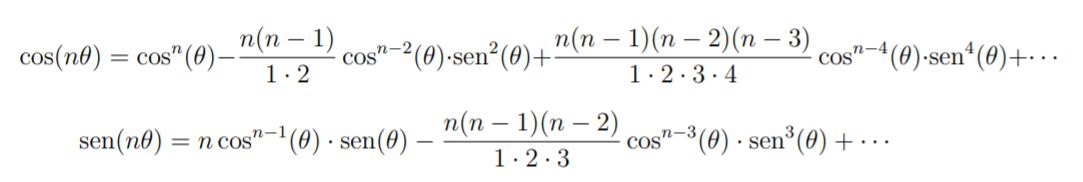
Y estas son justamente las sumas alternadas que habíamos anunciado para el seno y el coseno de nθ.

Para probar la igualdad propuesta para la tangente de nθ observamos que

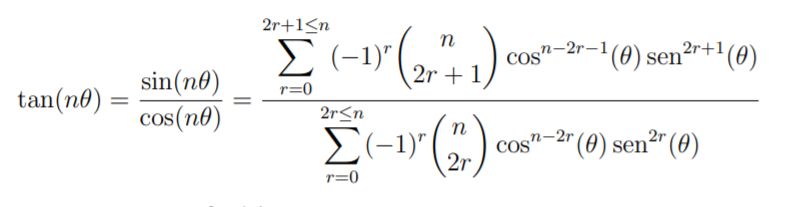
Y multiplicando numerador y denominador por cosn(θ), se deduce la fórmula de la tangente de nθ.

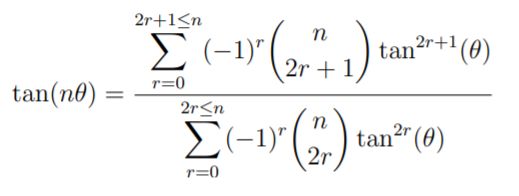
Parece difícil recordar esta fórmula un tanto compleja, pero será más sencillo si recurrimos al triángulo de Pascal.

Recordemos que en su Traité du triangle arithmétique (1654), Blaise Pascal iniciaba su texto con una página en la que dibujaba su triángulo aritmético. Le seguían casi un centenar de páginas en las que el matemático daba diecinueve propiedades de ese triángulo, bastante sencillas de demostrar en general. Pascal probaba algunas de ellas, otras las mostraba mediante un ejemplo y otras quedaban solo enunciadas.

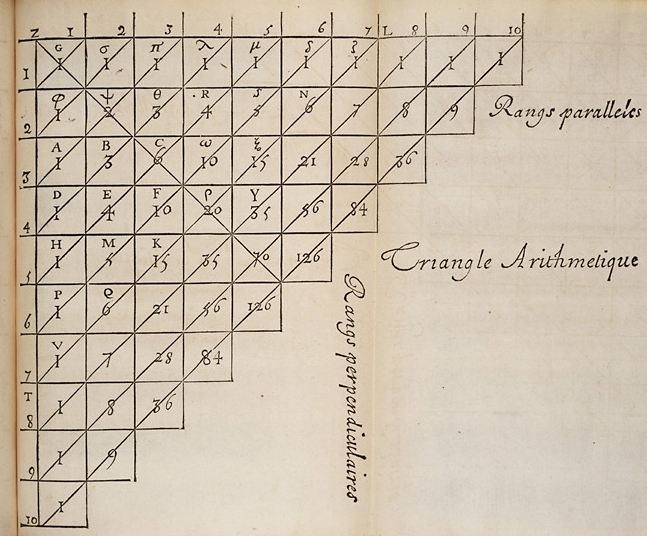El triángulo de Pascal (figura original de Pascal de 1654). Fuente: Wikimedia Commons

 

Ese triángulo, conocido hoy en día como triángulo de Pascal proporciona una manera de ordenar los coeficientes binomiales:

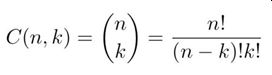
Recordemos que el coeficiente binomial C(n,k) es el número de grupos de k objetos que pueden elegirse en un conjunto formado por n objetos: Pueden calcularse por recurrencia, utilizando la llamada fórmula de Pascal:

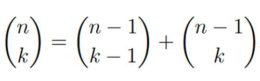
El triángulo de Pascal es el reordenamiento de los coeficientes binomiales desde el C(0,0) hasta el C(n,n), de manera que en la fila m aparecen –y en ese orden– C(m,0), C(m,1), C(m,2), …, C(m,m-1) y C(m,m).

Volvamos a la fórmula de la tangente de nθ antes obtenida. Observar que el numerador siempre comienza por C(n,1)tan(θ), los signos de los siguientes sumandos van alternando, la potencia de tan(θ) va aumentando de dos en dos y los coeficientes binomiales C(n,k) hacen lo propio.

En el caso del denominador, siempre se empieza por 1 (=C(n,0)tan0(θ)), los siguientes sumandos van alternando el signo, la potencia de tan(θ) va aumentando de dos en dos unidades y los coeficientes binomiales hacen lo propio.

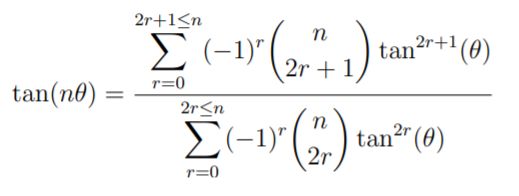
Para recordar la fórmula de la tangente denθ basta con colocarse en la fila n+1 del triángulo de Pascal –que es muy fácil de construir teniendo en cuenta la fórmula de Pascal– e ir moviéndose de manera alternada para ir recuperando los coeficientes del numerador y el denominador.

Lo hacemos en el caso de tan(8θ) para que se entienda mejor. La fórmula de tan(8θ) en términos de tan(θ) es –como hemos deducido antes–:

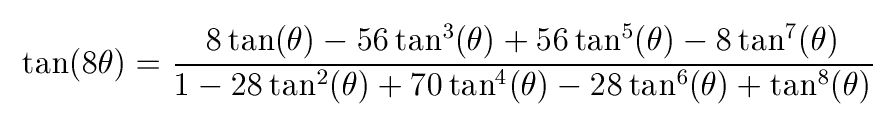
Nos colocamos en la fila 9 del triángulo de Pascal. Para obtener los coeficientes del numerador, comenzamos por el segundo dígito (en este caso 8) de la fila y vamos rescatando los números colocados en posición par. En la imagen hemos marcado en verde el coeficiente que va acompañado de un signo positivo y en rojo aquel que va con signo negativo en la fórmula (8, -56, 56, -8).

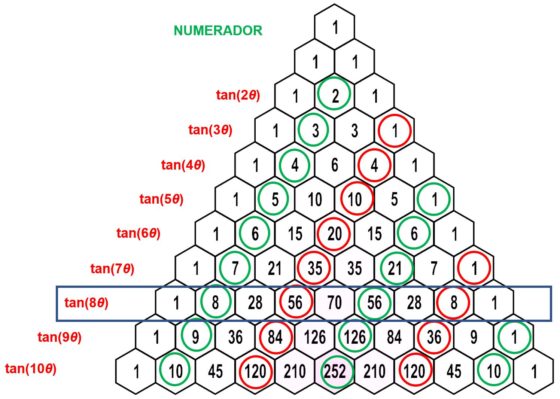
Para obtener los coeficientes del denominador, comenzamos por el primer dígito (el 1) de la fila y vamos rescatando los números que ocupan los lugares impares en esa fila. En la imagen hemos rodeado en verde los números que van acompañados de un signo positivo y de rojo aquellos que van con signo negativo en la fórmula (1, -28, 70, -28, 1).

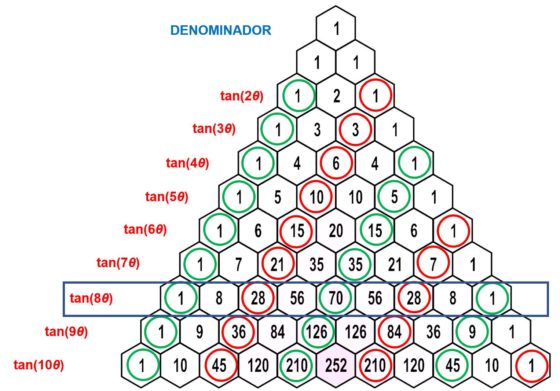
¡Una manera sencilla y hermosa de recordar el valor de la tan(nθ) en términos de tan(θ)!

Referencias

• Expansion of sin(nθ) and cos(nθ), Brilliant

• Frank C. Fung, An Approach to Mathematic Functions Basics (Section XLIII – Tangent Additions and the Pascal Triangle)

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad

El artículo El triángulo de Pascal para calcular tangentes se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Triangulando: Pascal versus Sierpinski
2. Blaise Pascal, Dios y la cicloide
3. Arte y geometría del triángulo rectángulo: Broken Lights

Foto:  Thor Alvis / Unsplash

En la tabla que vimos al hablar de las series de desintegración radiactiva se incorporaban los distintos periodos de semidesintegración para las distintas especies. Podemos comprobar que esos tiempos varían enormemente. Puede ser muy interesante que nos paremos un momento a reflexionar sobre este y otros aspectos del concepto de periodo de semidesintegración.

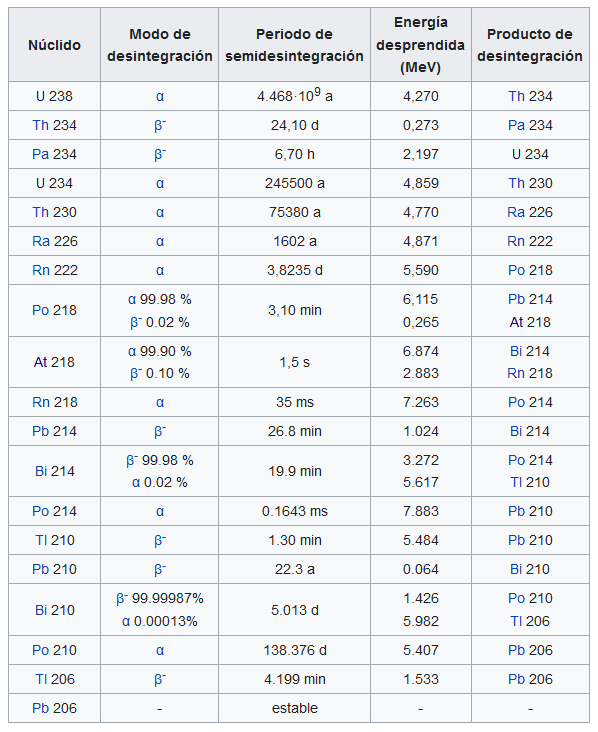Fuente: Wikimedia Commons

Para el 238U, la especie progenitora de la serie del uranio, el periodo de semidesintegración es de unos 4.500 millones de años. Esto significa que después de 4,5 ·109 años, la mitad de los átomos 238U se habrán desintegrado. Para el 214Po, el periodo de semidesintegración es del orden de 10-4 s; es decir, en sólo 1 / 10.000 de segundo la mitad de una muestra original de átomos de 214Po se habrá desintegrado. Si se dispusiera de muestras puras de cada uno, que contengan el mismo número de átomos, la actividad inicial (átomos que se desintegran por segundo) del 214Po sería muy alta y la del 238U muy débil. Sin embargo, si se dejara pasar solo 1 minuto, el polonio se habría descompuesto completamente a efectos prácticos y, por lo tanto, el número de sus átomos supervivientes sería tan pequeño que la actividad debida al polonio ahora sería menor que la actividad de los átomos de uranio.

De lo anterior podemos inferir que es posible que algunos elementos radiactivos, presentes en grandes cantidades hace mucho tiempo, se desintegrasen tan rápidamente que ahora no quedan rastros medibles. Por otro lado, muchos elementos radiactivos se desintegran tan lentamente que durante cualquier tiempo de experimentación ordinario las tasas de conteo que indican desintegración parecen permanecer constantes.[1]

Es importante recalcar las diferencias entre una población de, digamos, seres humanos, y una de átomos radiactivos. En un grupo de N0 bebés, la mitad puede alcanzar los 70 años; de estos N0 / 2 adultos mayores, es probable que ninguno celebre su cumpleaños número 140. Pero de los N0 átomos radiactivos con un periodo de semidesintegración de 70 años, en promedio N0 / 4 permanecerá intacto después de 140 años, N0 / 8 después de 210 años, etc. Para decirlo de otra manera, a diferencia de los humanos la probabilidad estadística de supervivencia de los átomos no cambia con “la edad” que ya han alcanzado. [2]

No podemos olvidar que al hablar de periodo de semidesintegración consideramos el comportamiento no de átomos individuales, sino de un gran número de ellos. Este método nos permite usar leyes estadísticas para describir el comportamiento promedio del grupo. Si cien mil personas lanzaran monedas simultáneamente solo una vez, se podría predecir con buena precisión que aproximadamente la mitad de ellas saldría cara. Pero no se podía predecir con precisión que una persona en concreto de esta multitud va a obtener cara en un solo lanzamiento. Si el número total de monedas lanzadas es pequeño (10, por ejemplo), es probable que el resultado observado difiera considerablemente de la predicción del 50% de caras que podríamos hacer con confianza si el número fuese cien mil.

En los experimentos con sustancias radiactivas se puede predecir que una cierta fracción de un número relativamente grande de átomos en una muestra sobrevivirá en un intervalo de tiempo dado (por ejemplo, la mitad sobrevivirá hasta alcanzar T1/2), pero no podemos predecir si un un átomo en concreto estará entre los supervivientes. A medida que la muestra de supervivientes disminuye en tamaño debido a las desintegraciones, las predicciones se vuelven menos precisas. Finalmente, cuando solo quedan unos pocos átomos sin cambios, ya no se pueden hacer predicciones útiles en absoluto. En resumen, la ley de desintegración es una ley estadística y, por lo tanto, es aplicable solo a grandes poblaciones de átomos radiactivos. Además, y esto es importante, no hace suposiciones sobre por qué los átomos se desintegran.

Notas:

[1] Es por esto que Becquerel no notó ningún cambio en la actividad de sus muestras de sal de uranio.

[2] En los seres humanos, por supuesto, la probabilidad de supervivencia (digamos, un año más) depende en gran medida de la edad, por lo que el concepto de «periodo de semidesintegración humana» no se puede utilizar en este caso.

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

El artículo La naturaleza estadística del periodo de semidesintegración se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Periodo de semidesintegración
2. La naturaleza estadística de la segunda ley de la termodinámica
3. La impureza, por definición, de las muestras radiactivas

Juanma Gallego

Los científicos han cuantificado el impacto del polvo del desierto en la población infantil de África, y han llegado a una conclusión preocupante: a pesar de ser una fuente natural de contaminación, el polvo aumenta considerablemente la tasa de mortalidad infantil.

Imagen 1: La mayor cantidad de polvo del mundo se genera en la Depresión de Bodele en el Chad, y ese polvo tiene gran incidencia en la salud, sobre todo en la salud infantil. (Fotografía: George Steinmetz)

El polvo nos ofrece paisajes espectaculares. Cuando hay polvo, podemos captar con nuestras cámaras atardeceres rojizos de gran belleza sin HDR o filtros especiales. En el País Vasco no es muy habitual este fenómeno, pero, según nos movemos hacia el sur, hay más posibilidades de verlo. Cerca del Sáhara, en las Islas Canarias, se aprecia perfectamente el efecto de este polvo. Nada más llegar al aeropuerto, al salir del avión, los viajeros que huyen del tiempo sombrío agradecen la bocanada de aire caliente. Y, con ella, la famosa calima. En un primer momento, como en la película Out of Africa, se agradece el toque exótico que da la calima, pero, con el tiempo, ese encanto inicial genera cierto malestar en la garganta y en los pulmones.

Son las dos caras de un mismo fenómeno: el lado positivo y el negativo. Al margen de la visión banal del turista, y centrándonos en el impacto que tiene a nivel mundial, también se aprecian esas diferencias. Comenzando por su lado positivo, los polvos que parten de los desiertos son fundamentales para fertilizar los ecosistemas de todo el mundo. El biólogo Eduardo Angulo explica en el artículo El polvo del Sáhara un artículo algunas de las funciones de estas nubes de polvo.

Aunque estas nubes se generan en muchos desiertos, el desierto del Sáhara es el mayor punto de partida de polvo del mundo. El polvo viaja a través del océano Atlántico, y llega hasta América en nubes perfectamente visibles por satélite. Es, sobre todo, a finales de la primavera y principios del verano cuando se dan las condiciones más propicias para que se generen este tipo de nubarrones, ya que en esa época las masas de aire oceánico son más frías, y elevan el polvo del Sáhara hacia capas más altas de la atmósfera.

Este tipo de nubes transportan, entre otros elementos, hierro y fósforo, componentes fundamentales tanto para las plantas terrestres como para el fitoplancton oceánico. En el caso de las plantas terrestres, es el Amazonas el que se beneficia especialmente de esta fertilización por vía aérea, pues sus tierras carecen de suficiente fósforo natural para mantener tanta biodiversidad.

En total, cientos de millones de toneladas de polvo atraviesan el océano cada año, pero este año ha sido especialmente notable. Según la información publicada en National Geographic, desde 1979 -año en el que comenzaron las observaciones por satélite-, la de este año ha sido hasta ahora la más densa. Por otro lado, algunos científicos creen que, al ser un aire tan seco, tiene un efecto contrario a la formación de huracanes, pues estas grandes tormentas necesitan aire húmedo para alimentar su enorme maquinaria meteorológica, y las nubes de polvo dificultan ese proceso.

Imagen 2: Investigadores de la Universidad de Stanford, Estados Unidos, que han estudiado la contaminación del polvo en África subsahariana han concluido que un aumento aproximado del 25% en las concentraciones de partículas medias locales ha causado un aumento del 18% en la mortalidad infantil. (Fotografía: stephlulu – Licencia Pixabay. Fuente: pixabay.com)

Por muy extenso que sea el Sáhara, la mayor parte del polvo no procede de las dunas, porque las partículas de arena que las componen son demasiado grandes como para recorrer largar distancias. El polvo se genera en otros puntos del desierto, sobre todo en zonas bajas capaces de almacenar partículas más pequeñas. La Depresión de Bodele en el Chad es una de las principales zonas: es más, es el centro de generación de polvo más importante del mundo. De media, hay tormentas de polvo 100 días al año.

Pues bien, un equipo de científicos ha centrado sus estudios en esa depresión para entender mejor la contaminación del aire en África. En una investigación realizada hace dos años, estos investigadores corroboraron que las partículas diminutas presentes en el aire (sobre todo las partículas PM2,5) causan numerosas muertes, especialmente entre los más pequeños: según los datos de 2015, ese año la exposición a estas partículas causó la muerte de 400.000 niños.

En esta ocasión, han analizado la relación entre el polvo y esas muertes. Los resultados publicados en Nature Sustainability ofrecen datos que requieren nuestra atención. Utilizando datos recogidos en 30 países del África subsahariana, se ha observado que un pequeño aumento de partículas en el aire eleva considerablemente las tasas de mortalidad infantil.

De acuerdo con los datos recogidos estos últimos 15 años, se han analizado las concentraciones de polvo en el África subsahariana, y se ha comparado esta información con los datos de natalidad, teniendo en cuenta un millón de nacimientos y los cambios en los niveles de partículas medidos por satélite. Argumentan que han visto una clara correlación. Según los resultados, el aumento del 25% de la concentración anual de partículas ha supuesto un aumento del 18% en la mortalidad infantil.

Son especialmente vulnerables a estas partículas aéreas los niños menores de cinco años. En una nota de prensa, han subrayado que en las últimas décadas en África se han producido grandes avances en materia de salud infantil, pero que, aun así, en algunas regiones las tasas de mortalidad infantil siguen siendo mayores de lo esperado. Esta diferencia ha sido atribuida al polvo.

Imagen 3: Las nubes de polvo son capaces de atravesar el océano. En la fotografía se aprecia una de esas nubes en junio sobre el Atlántico Norte captada por el satélite Suomi NPP. (Fotografía: NOAA/NASA)

Cómo no, los investigadores han tratado de cuantificar el impacto del cambio climático en esta materia, pero hay que recordar que la relación entre el polvo y el clima es compleja. Así, el polvo puede cumplir la función de una barrera, y dependiendo de la situación, esta barrera es capaz de reflejar la radiación solar, provocando un enfriamiento, pero también puede conllevar un calentamiento cuando capta el calor de la tierra. En cuanto al clima a nivel mundial, el impacto indirecto del polvo es aún mayor, sobre todo porque las fertilizaciones producidas gracias a este polvo permiten impulsar la eclosión del fitoplancton, lo que se traduce en una disminución del nivel de carbono en la atmosfera.

En cuanto a su influencia en África, estos expertos creen que la evolución del problema puede depender de las condiciones que se den en la Depresión de Bodele, zona del Chad donde se produce la mayor parte del polvo de África -y del mundo-. Así, los investigadores calculan que, dependiendo de los cambios que se den en las precipitaciones de esta depresión, la mortalidad infantil podría aumentar un 12% o disminuir un 13%.

Y han ido aún más lejos lanzando una propuesta audaz, de las que no se ven con buenos ojos en muchos sectores relacionados sobre todo con el medio ambiente: mojar la arena con el agua subterránea que hay en la comarca para que se genere menos polvo, utilizando para ello energía solar. Argumentan que, a menor escala, se ha realizado un proyecto similar en el valle californiano de Owens. Calculan que este tipo de riego habría evitado la muerte de 37.000 niños al año, ya que se produciría menos polvo. Según sus estimaciones, el «coste» de cada vida sería de 24 dólares y, teniendo en cuenta la situación socioeconómica actual de África, sostienen que sería más eficiente y realista que otras soluciones posibles.

Referencia:

Heft-Neal, S., Burney, J., Bendavid, E. et al. (2020). Dust pollution from the Sahara and African infant mortality. Nature Sustainability. DOI: 10.1038/s41893-020-0562-1

Sobre el autor: Juanma Gallego (@juanmagallego) es periodista científico.

Este artículo se publicó originalmente en euskara el 24 de julio de 2020 en el blog Zientzia Kaiera. Artículo original.

El artículo El polvo del Sáhara: fuente de vida y muerte se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. El polvo del Sáhara
2. El límite entre la vida y la muerte en las neuronas
3. De guijarro a asteroide en una trampa de polvo

 

Mercado en el Gueto de Varsovia (1941). Fuente: Albert Cuisian / Das Bundesarchiv

Dentro de unas semanas se cumplen ochenta años de la creación, por los ocupantes alemanes, del gueto de Varsovia. Agruparon en su interior a los judíos de la capital polaca y de otras ciudades de ese y otros países. El gueto era la estación previa al traslado al campo de Treblinka y otros campos de exterminio. Encerraron a algo más de cuatrocientas mil personas, casi la tercera parte de la población de Varsovia, en un espacio de 3,4 km2, el 2,4% de su superficie.

A finales de 1939 se habían registrado los primeros casos de tifus en la ciudad. Esa primera ola alcanzó su máxima incidencia en abril de 1940; para el verano ya se había disipado. El tifus es causado por la bacteria Rickettsia prowazekii, que transmiten los piojos; tiene un periodo de incubación de 14 días, provoca fiebre alta, dolor de cabeza y muscular, nauseas, escalofríos y sarpullidos extensos. Conforme progresa, aumenta la debilidad, se producen delirios, y pérdida de consciencia en algunos casos. Los peores desembocan en la muerte.

Una vez creado el gueto, las autoridades alemanas bloquearon el suministro de alimentos a su población, que tuvo que conformarse con lo poco que conseguía comprar el Consejo Judío. El hambre empezó a hacer mella, provocando muchas muertes por inanición. Aunque más adelante, en mayo de 1942, se levantó el bloqueo, la comida que suministraban los alemanes no llegaba al mínimo de subsistencia. En los meses siguientes, hasta julio de ese año, se registraron entre cuatro y cinco mil muertes al mes, aunque la cifra real debió de ser al menos el doble.

El tifus regresó a Varsovia justo tras la creación del gueto. La segunda ola fue peor. La salud de la gente se había deteriorado sobremanera como consecuencia de las restricciones severas de espacio, jabón y comida impuestas. Aunque oficialmente hubo veinte mil enfermos de tifus, la cifra real debió de rondar los cien mil, la cuarta parte de la población del gueto, tal y como atestiguan diferentes informes de la época. La enfermedad fue causa directa de unas veinticinco mil muertes, e indirecta de muchas más.

La incidencia del tifus creció a lo largo de 1941, hasta que en otoño empezó a remitir. Al llegar el verano siguiente había desaparecido. No era lógico que la epidemia detuviese su progresión al comienzo del otoño; lo esperable es que hubiese seguido creciendo hasta alcanzar una incidencia máxima al final del invierno de 1942. Un equipo internacional de investigadores ha utilizado modelos epidemiológicos para simular la dinámica de la epidemia de tifus y a partir de sus modelos han llegado a la conclusión de que el índice reproductivo básico del patógeno, el R0(t), alcanzó un máximo de casi 2,5 en mayo de 1941 y a partir de ese momento empezó a bajar, igualándose a 1 en enero de 1942 y llegando a cerca de 0,5 en julio de ese mismo año (si vale más de 1, la epidemia se extiende, si menos, retrocede).

Según los investigadores, fueron las actuaciones puestas en práctica por los judíos del gueto las que acabaron con la epidemia, incluso aunque muchas no pudieron ser implantadas de forma efectiva. Las principales se orientaron a formar a la población en higiene y salud, mantener limpias las estancias, promover el distanciamiento y aislar a los enfermos. Se salvaron así decenas de miles de vidas, quizás tantas como todas las que se habían perdido por hambre y enfermedad. Casi todos los supervivientes del gueto, más de doscientas sesenta mil personas, fueron deportadas a Treblinka, donde fueron asesinados. No se pudieron salvar del exterminio.

Fuente: Lewi Stone, Daihai He, Stephan Lehnstaedt, Yael Artzy-Randrup: “Extraordinary curtailment of massive typhus epidemic in the Warsaw Ghetto”. Science Advances 24 Jul 2020: Vol. 6, nº 30, eabc0927 doi: 10.1126/sciadv.abc0927

Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU

El artículo Epidemia en el gueto se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. La epidemia silenciosa del analfabetismo médico
2. ¿Cómo una bacteria inofensiva de Gambia acaba generando una epidemia en Wisconsin?
3. Dos años después

Anatomía del intestino delgado en un manual médico chino publicado en 1537, durante la dinastía Ming

En algunos libros antiguos de medicina china se encuentran tratamientos que tienen todo el sentido científico. El redescubrimiento de alguno ha dado lugar a la concesión de un premio Nobel, y otro, muy popular durante el XVI, salvó vidas. La base científica de este último, la sopa amarilla de la dinastía Ming, necesita de un Ignacio López Goñi para ser contada como merece.

Ignacio López Goñi es catedrático de microbiología y Director del Museo de Ciencias de la Universidad de Navarra.

La conferencia se impartió dentro del marco del festival Passion for Knowledge 2019 (P4K) organizado por el Donostia International Physics Center (DIPC).



Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus

El artículo Ignacio López Goñi – Naukas P4K 2019: La sopa amarilla de la dinastía Ming se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Naukas Bilbao 2017 – Ignacio López-Goñi: Las bacterias también se vacunan
2. Ignacio López Goñi – Naukas Bilbao 2018: La pandemia del siglo XXI
3. Ignacio López-Goñi: «El sistema de defensa de las bacterias es el mejor editor de genomas que existe»

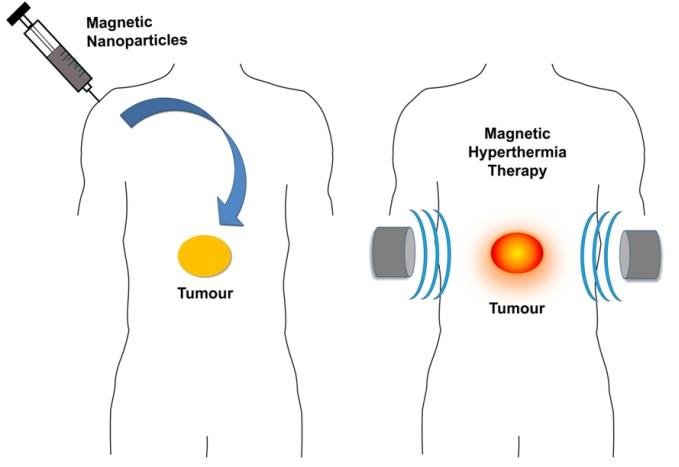Fuente: O.M. Lemine (2019) Magnetic Hyperthermia Therapy Using Hybrid Magnetic Nanostructures Hybrid Nanostructures for Cancer Theranostics doi: 10.1016/B978-0-12-813906-6.00007-X

Las células tumorales son más sensibles al calor que las células sanas. La hipertermia localizada podría ser, por tanto, una terapia contra el cáncer. Como los nanomateriales magnéticos presentan la capacidad de producir calor cuando son sometidos a campos magnéticos alternos, podrían emplearse nanopartículas magnéticas de tal manera que provocasen la muerte selectiva de las células tumorales sin dañar los tejidos sanos adyacentes. Podría ser una buena idea, en principio sin contraindicaciones, aunque aún presenta problemas de orden práctico, que se están abordando en ensayos clínicos.

Una de las mayores limitaciones de esta terapia experimental, denominada hipertermia magnética, es la tendencia de las nanopartículas magnéticas a aglomerarse, problema que se agrava cuando las nanopartículas se encuentran en un cuerpo vivo. La aglomeración conlleva una pérdida casi total de su capacidad para producir calor, convirtiéndolas en prácticamente inservibles.

Un grupo interdisciplinar de la Universidad del País Vasco ha creado un nuevo método que permitiría evitar la aglomeración de las nanopartículas. Los investigadores han demostrado in vitro que un adecuado recubrimiento de nanopartículas de magnetita (Fe3O4) con el copolímero PMAO-PEG impide que la capacidad de calentamiento de las nanopartículas decrezca en el medio celular.

La eficacia terapéutica de las nanopartículas recubiertas en cultivos de células de cáncer colorrectal también ha sido probada. El sistema induce la muerte celular total 48 horas después de la hipertermia.

Referencia:

Idoia Castellanos-Rubio, Irati Rodrigo, Ane Olazagoitia-Garmendia, Oihane Arriortua, Izaskun Gil de Muro, JoséS. Garitaonandia, Jose Ramon Bilbao, M. Luisa Fdez-Gubieda, Fernando Plazaola, Iñaki Orue, Ainara Castellanos-Rubio, Maite Insausti Highly Reproducible Hyperthermia Response in Water, Agar, and Cellular Environment by Discretely PEGylated Magnetite Nanoparticles (2020) ACS Applied Materials & Interfaces DOI: 10.1021/acsami.0c03222

Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa

El artículo Nanopartículas recubiertas para el tratamiento localizado del cáncer por hipertermia magnética se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Magnetosomas para el tratamiento del cáncer
2. Nanopartículas para reducir la metástasis hepática del cáncer de colon
3. Nanopartículas magnéticas contra células tumorales

Jesús Méndez

El 90 % de los docentes cree en ‘edumitos’, falsas ideas como los estilos de aprendizaje, que pueden perjudicar a sus alumnos. ¿Qué herramientas tiene el profesorado, aparte de su propia experiencia, para saber lo que funciona? Una iniciativa pionera en España se propone acercar a la escuela la evidencia sobre enseñanza de las ciencias.

Foto: Josh Manheimer / Pixabay

La educación científica está en apuros y los datos dan cuenta de la magnitud del problema: según la mayor encuesta realizada en España al respecto, la mayoría de los ciudadanos (51,2 %) considera que es difícil comprender la ciencia, y cuatro de cada diez españoles considera que el nivel de educación científica que ha recibido es bajo o muy bajo. Algo está fallando en el proceso.

“Hay un campo de la didáctica de las ciencias que trabaja investigando lo que funciona en educación, pero sabemos que sus conclusiones tardan una media de 50 años en llegar a las aulas”, comenta Digna Couso, física y doctora en didáctica de las ciencias. Ella es una de las coordinadoras del libro Enseñando ciencia con ciencia, publicado por iniciativa de la Fundación Española para la Ciencia y la Tecnología (FECYT) y la Fundación Lilly y que se puede descargar gratuitamente.

“Queríamos ofrecer un manual sencillo y bonito con lo que sabemos sobre lo que funciona y lo que no funciona en la educación de las ciencias”, explica Couso. El libro, en el que participan casi una veintena de especialistas, lanza mensajes concretos y accesibles junto con ejemplos prácticos de aplicación en las aulas.

La publicación forma parte de un plan más amplio desarrollado por FECYT para acercar la investigación y la práctica educativas, con acciones como un programa divulgativo en redes sociales y un curso online de formación del profesorado que podrán solicitar los centros de formación regionales.

Además, desmonta los mitos en torno a las prácticas educativas, los edumitos, generalmente bienintencionados pero erróneos que, según Marta Ferrero, maestra, psicopedagoga e investigadora sobre métodos educativos, “suponen una pérdida de tiempo, recursos e ilusión, y tienen un coste de oportunidad”. Estas creencias pueden repercutir negativamente, sobre todo en los estudiantes más desfavorecidos, y conllevan un alto coste en dinero y motivación que dejan de invertirse en métodos cuya eficacia ya ha sido probada.

Una ciencia próxima y argumentada

“El título de nuestro libro, Enseñando ciencia con ciencia, recoge dos sentidos diferentes”, precisa Couso. “Por un lado se refiere a que hay una ciencia de la enseñanza más allá del arte y la experiencia personal. Y también que para aprenderla hay que hacer ciencia en el aula, de forma análoga a como la hacen los propios científicos”.

No consistiría tanto en una educación basada en evidencias científicas, como a veces se denomina, sino en “una educación informada desde las pruebas”, precisa Ferrero. Porque “no se trata de supeditar la labor de los docentes, el protagonismo debe seguir siendo del profesorado. Pero la investigación sí que es una fuente de información para tomar decisiones. Una experiencia reflexionada tiene mucho valor”.

“Si tuviera que elegir tres mensajes —resume Rut Jiménez-Liso, profesora de didáctica de las ciencias en la Universidad de Almería y coordinadora también del manual— serían estos: que hay mucha investigación sobre lo que funciona y no funciona, que es muy importante mejorar la enseñanza de las ciencias para hacer ciudadanos críticos capaces de tomar decisiones fundamentadas; y que todos y todas podemos aprender ciencias, que el mundo que nos rodea puede tener sentido”.

La idea general que se tiene sobre la enseñanza de las ciencias es la de una transmisión directa de gran cantidad de conceptos, leyes y teorías. Sin embargo, los estudios recogidos en este manual abogan por un enfoque muy diferente basado en tres conceptos: indagación, modelización y argumentación.

A partir de preguntas que resulten cercanas o relevantes para los alumnos se produce un proceso en el que de forma activa buscan (indagan) pruebas que les permiten contrastar sus hipótesis, construyen explicaciones (modelos) basados en esas pruebas y las comparan (argumentan) para decidir cuál de ellas es más sólida o probable. Todo ello sin renunciar a sus ideas o modelos previos, sino activando precisamente esos conocimientos con los que vienen a la clase para luego construir a partir de ellos. Algo que es válido para todas las edades, incluso desde infantil.

“En todo el libro no hablamos de ninguna metodología concreta —explica Couso— porque hay muchas que incluyen los procedimientos clave, como la activación de ideas previas, la actividad e indagación sobre esas ideas, la discusión y la argumentación. De lo que se trata es de partir de lo que los alumnos saben y de que ellos sean los protagonistas de la construcción de conocimiento en el aula, sabiendo el docente en todo momento a dónde quiere llegar”.

¿Son todos los conocimientos científicos susceptibles de ser enseñados así?

“Todos lo son, porque todos los temas de ciencia están basados en pruebas —responde Rut Jiménez-Liso—, aunque es cierto que algunos pueden ser más áridos que otros. Lo que consigue este enfoque es evitar la repetida pregunta: ¿esto para qué me sirve a mí? ¿Para qué voy a estudiar los astros si yo no voy a ser astronauta? Si estudiamos por indagación el tema Sol-Tierra, los problemas no se basan en qué planetas componen el sistema solar, sino cuál es la mejor orientación de una casa, de una sombrilla, de unos paneles solares… Eso hace que cobre sentido para los estudiantes”.

“Quizá no todo se pueda enseñar así, pero entonces tampoco debería enseñarse”, matiza Couso. “Si quieres aprender el nombre de todos los huesos del esqueleto seguramente habrá métodos mejores, pero eso no es lo que los alumnos deberían aprender en la escuela, sino ideas profundas sobre el valor y la función del esqueleto”.

En educación, menos es más

En el libro se hace una defensa a ultranza del ‘menos es más’ en educación. “Las ideas potentes en ciencia son muy pocas, aunque luego sean muy complejas. Lo que se necesitamos son menos conceptos y más tiempo para trabajar esas pocas ideas en profundidad, porque eso es lo que deja huella. Al fin y al cabo lo que queremos son ciudadanos críticos y activos, que puedan participar en la toma de decisiones”, asevera Couso. Para ello deberían reducirse ostensiblemente los temarios, algo que ya está presente en los objetivos de la administración, pero que no se ha trasladado a los libros de texto, cada vez más extensos.

De la misma opinión es María Pilar Jiménez Aleixandre, catedrática de didáctica de las ciencias en la Universidad de Santiago de Compostela: “Resulta imposible abordar en clase todos los conceptos y teorías científicos. Lo importante es que el alumnado entienda cómo se ha llegado a algunos de ellos, seleccionados, lo que permite que en el futuro pueda entender cómo se ha llegado a otros”.

Porque “el objetivo, sobre todo para la mayoría del alumnado que no serán científicas o científicos profesionales, es que desarrollen el pensamiento crítico, que distingan entre opiniones sin fundamento y conocimiento apoyado en pruebas. En contextos de crisis, como pueden ser el cambio climático o la pandemia de covid-19, esta capacidad resulta esencial”.

La evaluación y las emociones

Uno de los capítulos del libro recoge consejos y pruebas sobre cómo debe ser la evaluación de los alumnos, teniendo en cuenta que su objetivo no es la calificación, sino el aprendizaje. De hecho, las notas numéricas no ofrecen información relevante.

Como escribe en su capítulo Neus Sanmartí, especialista en didáctica de las ciencias en la Universidad Autónoma de Barcelona: “Evaluar el grado de competencia requiere de la aplicación de criterios muy distintos de los tradicionales. Habitualmente se considera que un estudiante ha aprendido a un nivel mínimo cuando responde a la mitad de las preguntas en un examen, pero estos criterios de calificación no nos dicen si es competente”.

Además, si la evaluación va acompañada de una calificación, su efecto en el aprendizaje es nulo, porque los alumnos solo leen las cifras. Es más recomendable aplicar el concepto de rúbrica, detectar si el alumno alcanza un nivel de desempeño.

“Debemos aspirar a que los alumnos se coevalúen y autoevalúen —afirma Couso—, porque saben valorarse y son incluso más estrictos que los profesores. La evaluación debe ir dirigida a identificar lo que se ha hecho bien o mal, y a trabajar en cómo cambiar lo que no se ha hecho bien. Eso es exactamente lo que van a tener que hacer en su vida cuando el profesor ya no esté a su lado, porque no lo estará”.

Otro aspecto tratado en el libro es el papel de las emociones en el aprendizaje. Para Couso, “son sin duda importantes, pero no solo las positivas. Creo que ha pasado un poco como con las selfis, que han dado lugar a un solo tipo de fotos”.

En el libro se recoge que la enseñanza por indagación produce interés, concentración y satisfacción al reconocer que se aprende, pero se rechaza la idea de que deban promoverse solo emociones felices. Aprender conlleva emociones como el aburrimiento, inseguridad ante la pregunta planteada, resistencia a cambiar de ideas o incluso vergüenza por los planteamientos iniciales. Los docentes deben enseñar a reconocerlas y canalizarlas para reforzar las ganas de aprender.

Mucho más allá de las vocaciones científicas

El tipo de aprendizaje basado en los estudios y las pruebas promueve, más allá de unos conocimientos concretos, el fomento de un pensamiento crítico para todos que ayude a conocer el proceso de la ciencia, a tomar decisiones y a identificar afirmaciones pseudocientíficas. Eso ofrece la posibilidad de usar controversias para el aprendizaje en el aula y lleva a poner en más en contacto ciencias y humanidades.

Couso huye de la idea de que hay que fomentar vocaciones científicas: “No tenemos un problema de vocaciones, sino de diversidad. Los perfiles que llegan suelen ser muy homogéneos. Además, el concepto de vocación se aprovecha muchas veces para llevar a cabo una explotación: lo que debemos promover es una cultura de la profesionalidad. En cualquier caso, aunque aumentáramos mucho el número de profesionales relacionados con la ciencia, no llegarían a la mitad. ¿Es que el resto no tiene que saber ciencia?”.

El método de aprendizaje activo aquí propuesto no pretende formar científicos en miniatura, sino profanos competentes que puedan utilizar los conocimientos adquiridos en la vida real. A la vez, y sin forzarlos, al diseñar soluciones a problemas, construir modelos y evaluar afirmaciones, interiorizan que pueden llegar a ser científicos o ingenieras y promueven la sensación de autoeficacia.

Capítulo aparte merece también la enseñanza sin estereotipos de género, teniendo en cuenta que las niñas a los seis años ya piensan que son menos inteligentes que sus compañeros varones y que a los 10 o 12 muchas ya han descartado estudiar opciones de ciencia o tecnología.

Un futuro prometedor

“En cualquier debate aparece y se habla de la importancia de la educación —añade Couso—, pero siempre acaba prevaleciendo la fuerza de la anécdota o de la experiencia, cuando en realidad tenemos desde hace muchos años evidencias sobre cosas que funcionan y cosas que no lo hacen”.

La experiencia puede servir de ayuda en ocasiones, pero “no basta con ella, al igual que no basta con saber de ciencia para enseñarla bien” completa Couso, que lanza un mensaje final sobre la situación actual de la educación en ciencias: “En general, y cuanto mayores son los alumnos, las clases tienden a ser menos activas, más proclives a un consumo pasivo de conocimiento. Los docentes necesitan tiempo y que se les cuide, porque estamos en una situación muy prometedora, veo renovación, ganas y mucha motivación. Nuestra área de influencia desde la didáctica es muy pequeña y nos cuesta tener relevancia, pero cuando los profesores se acercan a estos métodos se entusiasman, porque ven que funcionan”.

Los edumitos perjudican gravemente al alumnado

“Tenemos un problema”, reconoce Ferrero. “Los estudios indican que algunos neuromitos en la educación son aceptados por más del 90 % de los docentes, como la creencia de que una estimulación extraordinaria aumenta el rendimiento cognitivo o que adaptar la forma de enseñar a los estilos de aprendizaje de los alumnos mejora los resultados”.

Este mito tan extendido tiene que ver con la aplicación de la teoría de las inteligencias múltiples, propuesta por el psicólogo y pedagogo Howard Gardner. “Pero no hay ninguna prueba de su utilidad. Más aún, muchos centros lo aplican de una forma que Gardner consideraría inadecuada”, explica Ferrero.

También existe la creencia de que los niños de hoy son nativos digitales, cuando en realidad “no usan la tecnología de forma diferente. Hay que enseñarles explícitamente a utilizarla. Hay pruebas claras de que no saben hacer búsquedas de forma correcta, no analizan bien el contenido ni su veracidad”.

¿Por qué ha tenido lugar la extensión de estos mitos y por qué no hay más lugares donde buscar pruebas contrastadas y adaptadas al profesorado? “La academia y las escuelas han estado tradicionalmente de espaldas una a la otra”, opina Ferrero, quien apunta algunas iniciativas útiles para los docentes, como Las pruebas de la educación, un repositorio internacional ofrecido por EduCaixa o una serie de publicaciones a cargo de la Fundació Jaume Bofill.

Este artículo se publicó originalmente en SINC. Artículo original.

El artículo Menos conceptos y más pensamiento crítico para mejorar la educación científica en el aula se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Por qué la filosofía es tan importante para la educación científica
2. Por qué los colegios no deberían enseñar habilidades de pensamiento crítico generales
3. Autismo y educación: problemas y pautas en el aula

 En la primera entrega de la serie Arte Moebius (I) en el Cuaderno de Cultura Científica, después de explicar brevemente qué es una banda de Moebius, algunas de sus curiosas características –que posee una sola cara y un solo borde– y un pequeño experimento para realizar en casa, habíamos dedicado la entrada a mostrar unos cuantos ejemplos de esculturas basadas en esta curiosa superficie. Los artistas mencionados en dicha entrada fueron Max Bill, José Ramón Anda, John Robinson, Jeremy Guy, Vladimir Vasiltsov y Eleonora Zharenova, A. Z. Nalich, Ernst Neizvestny, Mariko Mori y Chambliss Giobbi.

Superficie sin fin (1974-75), del escultor suizo Max Bill. Imagen de Modern Design

 

En la presente entrada vamos a seguir realizando un recorrido por algunas interesantes, curiosas y hermosas esculturas inspiradas en la superficie de una sola cara y un solo borde.

Para empezar, vamos a reiniciar este paseo artístico matemático con el mismo escultor con el que terminamos la entrada anterior, el estadounidense Chambliss Giobbi (Nueva York, 1963). Este artista neoyorkino trabaja con diferentes perspectivas sobre la banda de Moebius en una serie de esculturas, que son móviles, en las que utiliza coches de juguete para crear collages tridimensionales.

En su escultura Circunvalación de Moebius (2012), que mostramos en la entrada Arte Moebius (I), la estructura que subyace es un prisma cuadrado “flexible” rotado media vuelta y pegado por los extremos generando una doble banda de Moebius, además colocado para formar el símbolo del infinito (la curva llamada Lemniscata de Bernoulli). En su escultura Hoja de trébol de Moebius (2013) la forma que tiene la escultura es un nudo de trébol. Y finalmente la escultura móvil Rampa de salida de Moebius (2012), que podéis admirar más abajo y que me recuerda a otro de los curiosos experimentos relacionados con esta superficie.

Rampa de salida de Moebius (2012), del artista estadounidense Chambliss Giobbi. Imagen de la página web de Chambliss Giobbi

Veamos el mencionado experimento. Para realizar este necesitamos únicamente una hoja de papel, de hecho, nos vale con una tira alargada con la que construir una banda de Moebius, un poco de cinta aislante para pegar los extremos de la cinta de papel y unas tijeras. Mientras que en la anterior entrada habíamos explicado lo que ocurría en una cinta normal y en una de Moebius cuando se cortan longitudinalmente las bandas por la mitad, ahora veremos qué ocurre si cortamos longitudinalmente las bandas, pero por una tercera parte de su anchura (véase el artículo de Marta Macho, Listing, Möbius y su banda ).

Cuando cortamos longitudinalmente una banda normal por un tercio de su altura el resultado son dos bandas normales, de la misma largura, pero anchuras distintas, una un tercio y otra dos tercios de la anchura original. Mientras que en el caso de una banda de Moebius el resultado son una banda de Moebius, igual de largo y con una anchura de un tercio de la original, y una banda normal retorcida, con el doble de largo y un tercio de ancho, ambas entrelazadas.

La escultura de Giobbi nos recuerda a este experimento, pero el escultor de Nueva York habría intercambiado las larguras, en la anterior escultura la banda de Moebius con coches de juguete tiene el doble de largura que la banda normal, y es mucho más ancha.

El siguiente escultor que quiero que nos encontremos en este paseo es el artista británico Richard Fox (1965) que, como muchos otros escultores interesados en la superficie de Moebius, trabaja tanto con la banda de una cara, como con la de dos caras. Richard Fox tiene dos series de esculturas, realizadas en bronce una y en mármol blanco otra, tituladas Moebius, una de las cuales vemos en la siguiente imagen.

Moebius V (2018), del artista británico Richard Fox, realizada en bronce y de tamaño 50 x 47 x 40 cm. Imagen de la página Jenna Burlingham Fine Art

 

Pueden verse más obras de la serie en la página web de Richard Fox. Así mismo, tiene dos series de obras tituladas Ravel (enmarañar o enredar), que son bandas normales con dos caras. En una de las series, White Ravel, cada una de las caras con un color diferente, blanco y arena.

White Ravel in A, XVI (2016), del artista británico Richard Fox, realizada en sicomoro con pigmento de tierra blanca y base de piedra arenisca. Imagen de la página web de Richard Fox

Para la exposición OneOak/Unroble, que tuvo lugar en el Real Jardín Botánico de Edimburgo en 2012, Richard Fox realizó una banda de Moebius anudada, como un nudo de trébol, en madera de roble.

Nudo de trébol de Moebius (2012), del artista británico Richard Fox, realizada en madera de roble. Imagen de la página de Syva Foundation

 

Otro artista que trabaja con la superficie de Moebius, así como con otras superficies geométricas y nudos “topológicos” es el escultor californiano T Barney, del que podéis admirar sus hermosas esculturas en la página T Barney Sculptures. Vamos a mostrar aquí dos ejemplos realizados en distintos materiales, piedra y bronce.

La primera escultura es Siringa (ninfa mitológica de Arcadia), realizada en piedra, en concreto, en arenisca de Arizona.

Siringa (ninfa mitológica de Arcadia), del artista estadounidense T Barney, realizada en arenisca de Arizona. Imagen de su página T Barney Sculptures

 

Podéis disfrutar de un video en el que se ve la escultura en movimiento, con algunos detalles de la misma, en particular, puede observarse el parecido de este material, arenisca de Arizona, con la madera, con la cual en ocasiones se confunde.

La siguiente escultura es Tisbe (figura femenina de la mitología griega), realizada en bronce con una pátina de jade (en la siguiente imagen), rubí, zafiro o turquesa.

Tisbe (figura femenina de la mitológica griega), del artista estadounidense T Barney, realizada en bronce con una pátina de jade. Imagen de su página T Barney Sculptures

 

Ypodéis disfrutar de un video en el que se ve la escultura en movimiento, con algunos detalles de la misma.

En el año 2000 celebramos en Bilbao el Congreso Internacional de Geometría Diferencial en memoria de Alfred Gray, dedicado al matemático estadounidense Alfred Gray (1939-1998) que había fallecido en otoño de 1998 durante una estancia de investigación en la Universidad del País Vasco/Euskal Herriko Unibertsitatea. Uno de los invitados del congreso fue el escultor Helaman Ferguson, amigo de Alfred Gray, con quien este había colaborado para la realización de una serie de esculturas sobre la superficie minimal de Costa. Por este motivo, Helaman Ferguson realizó para el congreso una escultura con la superficie de Costa, The Alfred Gray Memorial Bronze D4, K 0 (2000).

The Alfred Gray Memorial Bronze D4, K (2000), del artista Helaman Ferguson, realizada con motivo del Congreso Internacional de Geometría Diferencial en memoria de Alfred Gray.

 

Pero la pieza más conocida de este escultor es Umbilic Torus / Toro umbilical (1988), que es una obra relacionada con la banda de Moebius. Expliquemos la estructura de la misma.

Recordemos que para construir una banda de Moebius tomamos una tira plana (de papel), giramos media vuelta uno de los extremos y lo pegamos al otro extremo. Imaginemos ahora que disponemos de un prisma triangular, largo y flexible (para poder manipularlo, aunque sea en nuestra imaginación), que giramos 120 grados, es decir, un tercio de vuelta, uno de los extremos y lo pegamos al otro extremo –triángulo extremo contra triángulo extremo-, entonces tendremos una figura geométrica que solamente tiene una cara. Esto se debe a que cada cara del prisma se continúa con la siguiente donde se juntan los extremos, tras el giro de 120 grados. Esta es la figura con la que trabajaba también el escultor británico John Robinson en su obra Eternidad (1980) y que vimos en la entrada anterior, Arte Moebius (I).

Para la escultura Toro umbilical, Ferguson utiliza no un prisma triangular, sino un prisma de deltoide, una curva de tipo triangular. A continuación, se muestra una ilustración de la curva conocida como deltoide (que realmente es la trayectoria de un punto de una circunferencia que rueda, sin deslizarse, dentro de otra circunferencia más grande, de tres veces su radio) y otra de la figura geométrica generada con el prisma de deltoide.

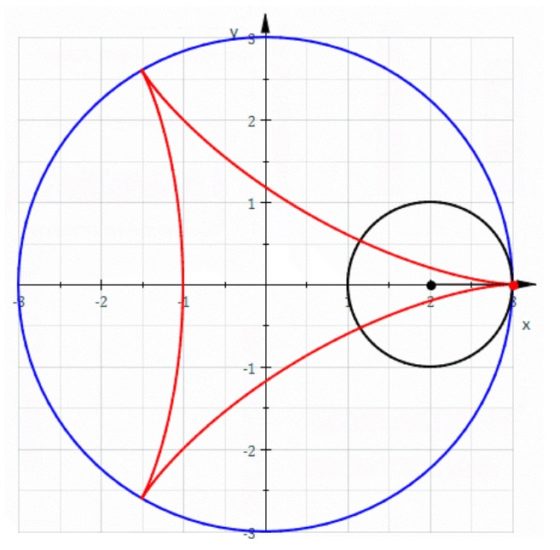Deltoide. Imagen de Wikimedia Commons

 

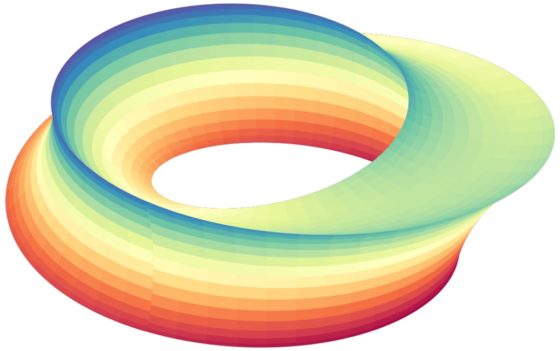Toro Umbilical. Imagen de Wikimedia Commons

 

Finalmente, la superficie de la escultura no es lisa, sino que Helaman Ferguson ha añadido la forma de la curva fractal de Hilbert, que es una “curva que rellena el plano” (aunque en esta entrada no entraremos en las cuestiones matemáticas de esta curva fractal; puede verse su construcción en la entrada Fractus, arte y matemáticas). Esta curva se define por un proceso iterativo infinito y el escultor incluye una de las primeras iteraciones para que la curva sea visible.

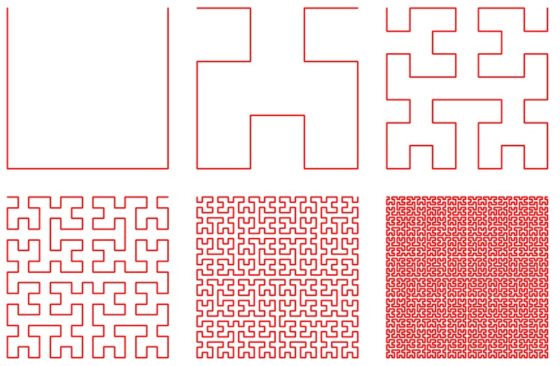Seis primeras iteraciones de la curva de Hilbert. Imagen de Data Genetics

 

Finalmente, el resultado del trabajo de Helaman Ferguson fue la escultura Toro umbilical (1988), que podemos ver aquí.

Toro umbilical (1988), de Helaman Ferguson. Imagen de ACM Siggraph

 

En la página web de Helaman Ferguson podéis ver una versión que realizó en 2012 del Toro Umbilical, en bronce, de 8,5 metros de altura, y que está en el exterior del Centro Simons de Geometría y Física de la Universidad Stony Brook.

A continuación, me gustaría hablar de dos escultores muy interesantes y que utilizan la banda de Moebius de una forma muy particular, representando en la escultura el espacio alrededor de este objeto geométrico, en lugar de la propia superficie. Son el artista estadounidense John Ernest (1922-1994) y el artista japonés Keizo Ushio.

Keizo Ushio (Fukusaki, Prefectura de Hyogo, 1951) es un artista con una obra escultórica muy geométrica, que al igual que algunos otros artistas mencionados en este paseo, ha llamado fuertemente la atención de la comunidad matemática.

Conocí a Keizo Ushio en el International Congress of Mathematicians que organizamos en Madrid en agosto de 2006, cuando le invitamos a realizar una escultura en vivo en el exterior del Palacio Municipal de Congresos de Madrid.

El escultor Keizo Ushio y el matemático Raúl Ibáñez en el exterior del Palacio Municipal de Congresos en Madrid, junto a la escultura Oushi-Zokei ICM Madrid 2006 en proceso de realización

 

En la escultura Möbius in Space (2005) de Keizo Ushio, que mostramos más abajo, y en otras obras similares, el objetivo del artista no es representar la superficie de una sola cara y un solo borde, sino el espacio exterior que rodea a la misma. De manera que la cinta de Moebius es el “espacio vacío” en la escultura. El problema de esta idea es hacer visible esa superficie que no está y que está dentro de ese “espacio exterior”. Para ello, Keizo Ushio trabaja con el objeto geométrico tridimensional conocido en matemáticas como toro sólido. El toro es la superficie generada por una circunferencia que gira alrededor de un eje en el mismo plano de la circunferencia, y que esencialmente es la forma de un flotador, de manera que el toro sólido es el objeto tridimensional cuyo exterior es el toro, por lo que es como un donut.

El toro es una superficie geométrica que está generada por una circunferencia que gira alrededor de un eje. Imagen de Wikimedia Commons

 

El toro sólido va a jugar el papel de “espacio exterior” de la banda de Moebius, por lo tanto, tenemos que pensar en la banda de Moebius dentro del toro sólido.

Para entenderlo mejor, pensemos primero en la banda normal dentro del toro. Si consideramos todos los diámetros verticales de las circunferencias que rotadas forman el toro, estos segmentos forman una banda normal (dos caras y dos bordes), cuya anchura es el diámetro de esas pequeñas circunferencias del toro. ¿Cómo se obtendrá la banda de Moebius? Si consideramos primero un diámetro vertical y luego para las demás circunferencias del toro se van considerando los diámetros que van girando, desde ese vertical, de forma que al llegar al lugar de partida han dado medio giro, luego de nuevo es el diámetro vertical, esos segmentos forman una banda de Moebius dentro del toro. Pensemos que los segmentos representados en la siguiente imagen son los diámetros, que han girado media vuelta, de las circunferencias del toro, luego efectivamente es una banda de Moebius dentro del toro.

¿Cómo realiza Keizo Ushio este tipo de esculturas? Empieza con un bloque rectangular –con forma de paralelepípedo- de granito (suele trabajar con diferentes tipos de granito), que moldea con un martillo neumático hasta conseguir dejarlo con la forma de un toro sólido. Una vez conseguido el toro se trata de barrenar con el martillo neumático los diámetros que corresponden a la banda de Moebius.

El escultor japonés Keizo Ushio, durante el International Congress of Mathematicians Madrid 2006, barrenando el toro para formar el vacío de uno de los diámetros del toro para realizar la escultura Oushi-Zokei ICM Madrid 2006

 

Antes de continuar, veamos con un experimento casero qué pasaría en el caso de barrenar una banda normal dentro del toro sólido, como la descrita anteriormente. Para ello hemos cogido un donut (toro sólido), luego con un palillo chino (la barrena) hemos barrenado el donut (toro), pero con los diámetros verticales, creando un espacio vacío en el toro que es el vacío de “la banda normal”, que como tiene dos caras deja al exterior, el donut, con dos partes, la de fuera y la de dentro.

En el caso de la escultura Möbius in Space (2005) se barrenan los diámetros dando media vuelta, es decir, formando el vacío de la banda de Moebius, que como solo tiene una cara, el espacio exterior no puede dividirse en dos partes y es una sola pieza. En la siguiente ilustración, del profesor estadounidense de Ciencias de la Computación Carlo H. Séquin (véase Sculpture Designs by Carlo Sequin Inspired by Keizo Ushio), vemos un diagrama de esta idea.

El resultado de todas las ideas anteriores, es la escultura de Keizo Ushio, Möbius in Space (2005). En este caso, como el artista ha pintado el borde del espacio vacío, el impacto visual de la escultura es mayor.

Möbius in Space (2005), de Keizo Ushio, realizada en granito y con un tamaño de 3,2 x 3 x 2 metros. Imagen del Wall Street Journal [https://www.wsj.com¿Qué es lo que ocurriría en la anterior construcción si en lugar de barrenar los diámetros del toro girando media vuelta, lo hiciera ggirando una vuelta entera? Entonces tendríamos una banda normal –dos caras y dos bordes- retorcida. Por este motivo, en las esculturas de Keizo Ushio en las que barrena los diámetros del toro girados una vuelta entera la zona vacía es una banda normal retorcida, con dos caras, luego la escultura se separa en dos partes. Esto es lo que ocurre por ejemplo en la escultura Oushi-Zokei ICM Madrid 2006. Muchas personas relacionan esta escultura con la banda de Moebius, pero realmente es una banda normal retorcida, por eso se separa en dos partes.

Oushi-Zokei ICM Madrid 2006, del escultor Keizo Ushio, realizada durante el International Congress of Mathematicians Madrid 2006

 

La siguiente escultura, Dream Lens (2003), está realizada barrenando diámetros en el toro girando vuelta y media, desde el primero hasta volver al mismo, de forma que la parte vacía del toro es una banda de Moebius retorcida.

Dream Lens (2003), del escultor Keizo Ushio, realizada en granito azul y de tamaño 0,8 x 3 x 2 metros

 

Aunque podríamos hablar muchísimo más de la obra de este genial escultor japonés, vamos a terminar con una serie de esculturas en las cuales tanto el espacio exterior, como el espacio vacío, son bandas de Moebius. Una de las piezas de esta serie es la escultura Möebius in space (1990), que mostramos a continuación.

Möebius in space (1990), de Keizo Ushio, realizada en granito negro africano y con un tamaño de 2 x 2 x 1 metros, que está en Mihama, prefectura de Fukui

 

La escultura Banda de Moebius (1971-72), del artista constructivista abstracto británico John Ernest (1922-1994) está basada en una idea similar a la de la escultura Möbius in Space (2005) de Keizo Ushio, aunque con un tratamiento más rectilíneo. El espacio exterior es un paralelepípedo con un “agujero” en medio, de manera que es “topológicamente” como un toro sólido. El espacio vacío es una banda de Moebius, pero colocada de forma más rectilínea dentro del espacio en el que está, con el objetivo de que en la imagen global, de frente, veamos un cuadrado dentro de otro cuadrado. El resultado es una pieza impactante.

Banda de Moebius (1971-72), del artista británico John Ernest, realizada en Madera, metal, contrachapado y pintura alquídica, con un tamaño de 2,44 x 2,14 x 0,58 metros. Pertenece a la colección de la Tate Gallery de Londres. Fotografía de Paul y Susan Ernest, en la página de la Tate Gallery

 

Volvamos a las representaciones de la propia banda de Moebius, pero en esta ocasión se trata de una escultura curiosa y colaborativa. La siguiente artista utiliza el material reciclado para crear sus obras de arte, es la artista valenciana Rosa Montesa. Como la propia artista explica en su página web, sobre esta escultura:

Esta escultura es un encargo de AIMPLAS [Centro Tecnológico en el sector del plástico]. El objetivo era que los trabajadores pudieran realizar colectivamente una pieza escultórica. La figura sobre la que están puestas las botellas es una Cinta de Moebius.

Cinta de Moebius realizada con material reciclado, botellas de plástico, a partir del diseño de la artista valenciana Rosa Montesa. Imagen de la web de Rosa Montesa

 

Para terminar, una pequeña sorpresa, al menos para algunas de las personas que estéis leyendo esta entrada. El artista surrealista catalán Salvador Dalí, que siempre estuvo muy interesado por las matemáticas y la ciencia, también quedó cautivado por la cinta de Moebius.

Algunos de los grifos del Castillo Gala Dalí, o Castillo de Púbol, tienen diseños con la banda de Moebius. Por ejemplo, los grifos de la bañera de la sala de baño de Gala, que era la antigua cocina de este castillo gótico.

Grifos de oro macizo de la bañera de la sala de baño de Gala, en el Castillo Gala Dalí, diseñados por Salvador Dalí a partir de la cinta de Moebius. Imagen de la guía secreta del Museo Dalí en Instagram

 

Así mismo, Salvador Dalí diseñó en 1970 una escultura con la forma de la Banda de Moebius, para ser realizada en pasta de vidrio por la casa Daum.

Escultura de pasta de vidrio, diseñada por Salvador Dalí a partir de la cinta de Moebius y realizada por la casa Daum. Imagen de The Dalí Universe

 

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

El artículo Arte Moebius (II) se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Arte Moebius (I)
2. El teorema de Pitágoras en el arte
3. Arte y geometría del triángulo rectángulo: Broken Lights

Foto:  Brian Suh / Unsplash

Cuando hablamos de la impureza de las muestras radiactivas pusimos como ejemplo que, de 1,000,000 de átomos de 218Po presentes en una muestra recién preparada, solo quedarían alrededor de 10,000 después de 20 min, y el resto se habría desintegrado en átomos de 214Pb y sus productos hijos. Solo 3 minutos después de la preparación de la muestra pura de 218Po el 50% de los átomos originalmente presentes en la muestra se habrían desintegrado. En el caso del radio (226Ra), la mitad de los átomos de radio en una muestra recién preparada de radio tardaría 1620 años en transformarse en átomos de radón.

Estos dos ejemplos ilustran el hecho experimental de que las muestras de elementos radiactivos presentan una gran diferencia en sus velocidades de desintegración. Estas diferentes velocidades son el resultado promedio de muchos eventos individuales de desintegración diferentes que ocurren al azar en una muestra. Si nos centramos en un átomo concreto de cualquier elemento radiactivo, nunca podemos saber cuándo se desintegrará; algunos pueden desintegrarse tan pronto como se producen, mientras que otros puede que nunca se desintegren. Aún así, se ha encontrado experimentalmente que dada una muestra que contenga átomos radiactivos de un mismo tipo [1], la fracción de estos átomos que se desintegra por segundo es inmutable [2] y siempre la misma para un número lo suficientemente grande de átomos de ese tipo. [3] Esta fracción es casi completamente independiente de todas las condiciones físicas y químicas, como temperatura, presión o combinación química. [4]

Este hecho experimental tiene consecuencias muy importantes. Digamos, por ejemplo, que 1 de cada 1000 de los átomos de una muestra pura recién preparada se desintegra durante el primer segundo. Entonces, cabe esperar que 1 de cada 1000 de los átomos restantes se desintegre durante el siguiente segundo. Igualmente, 1/1000 de los átomos que quedasen después de 10 s se desintegrarán durante el undécimo segundo, y así sucesivamente. De hecho, durante cualquier segundo siguiente, 1/1000 de los átomos que quedan al comienzo de ese segundo se desintegrarán, al menos hasta que el número de átomos restantes no sea lo suficientemente grande y que las predicciones se vuelvan muy inciertas.

Dado que la fracción de átomos que se desintegra por unidad de tiempo es una constante para cada tipo de átomo, el número de átomos que se desintegran por unidad de tiempo disminuirá en proporción al número decreciente de átomos que aún no han cambiado. En consecuencia, si hacemos una gráfica del porcentaje de átomos inalterados supervivientes en función del tiempo, se obtiene una curva como la de la figura siguiente.

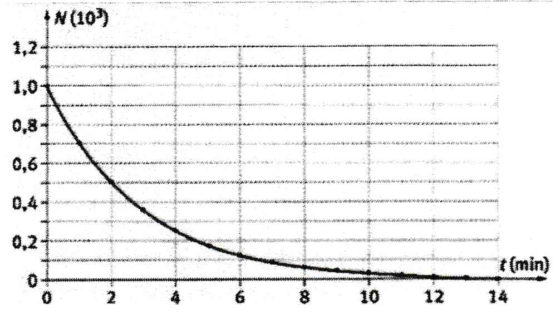Gráfica de la desintegración de una especie radiactiva con periodo de semidesintegración de 2 minutos. Fuente: Wikimedia Commons

El número de átomos en una muestra que se desintegra por unidad de tiempo se denomina actividad de la muestra. Por lo tanto, la gráfica también representa la forma en que la actividad medida de una muestra disminuiría con el tiempo. La curva que muestra el número de átomos que no se han desintegrado aun en función del tiempo se aproxima asintóticamente al eje del tiempo; es decir, el número de átomos supervivientes se reduce, pero solo se acerca a cero [5]. Esta es otra forma de decir que no se puede asignar un “tiempo de vida” definido en la que todos los átomos originales de una muestra se habrán desintegrado.

Sin embargo, es posible especificar el tiempo requerido para que se desintegre cualquier fracción cualquiera y arbitraria de una muestra, la mitad, un tercio o el 67%, por ejemplo. Por conveniencia a la hora de hacer comparaciones, se optó en su momento por la fracción 1/2. Rutherford denominó half-life, periodo de semidesintegración [6], al tiempo necesario para la desintegración de la mitad de los átomos originales de una muestra pura (símbolo T1/2). Cada tipo de átomo radiactivo tiene un periodo de semidesintegración único [7].

Notas:

[1] Para muestras de un mismo isótopo. Introducimos el concepto de isótopo más adelante en la serie, por lo que ahora preferimos la perífrasis.

[2] En el sentido de que no puede alterarse.

[3] Esta frase en negrita es fundamental para comprender la radiactividad.

[4] Este hecho convierte a algunas especies radiactivas en excelentes relojes para distintos usos. Probablemente la técnica más conocida que hace uso de uno de estos relojes es la datación por carbono-14.

[5] Lo de que es una curva asintótica es una simplificación. Conforme la muestra se hace más pequeña nos encontraremos fluctuaciones estadísticas que serán significativas, por lo que la curva ya no será tal, sino una serie de escalones.

[6] Hay que apresurarse a decir que half-life no es vida media, sino semivida. Vida media es un concepto de física de partículas y se refiere a una partícula concreta. En radiactividad hablamos de una población de átomos, por tanto de semivida y, más concretamente de periodo de semidesintegración.

[7] Lo que implica que el periodo de semidesintegración de un elemento se puede utilizar para identificar el tipo de elemento radiactivo.

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

El artículo Periodo de semidesintegración se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. La impureza, por definición, de las muestras radiactivas
2. La radiactividad no es una reacción química
3. Un modelo simple de gas

Santiago Pérez Hoyos

Atmósfera de Venus a partir de datos tomados por el AKATSUKI Ultraviolet Imager (UVI). Fuente: ISAS/JAXA – Wikimedia Commons

El descubrimiento en nuestro infernal vecino Venus de una molécula considerada como biomarcador o “huella de la vida”, el fosfano, ha sorprendido a los científicos que trabajamos en las atmósferas planetarias. Recuperados del primer impacto y tras los ríos de tinta que han corrido, tanto elogiando como rebajando el descubrimiento, llega el momento de reflexionar sobre los siguientes pasos que debemos dar para llegar a una respuesta concluyente.

Comenzamos con el más evidente: la detección de fosfano debe ser replicada.

Los compuestos químicos atmosféricos dejan en la luz una serie complicada de líneas que los identifican inequívocamente. Detectar más líneas, en regiones diferentes del espectro y con la mayor claridad posible, será el primer objetivo. No solo del equipo que anunció la detección, sino también de otros investigadores que ya se han puesto manos a la obra.

Hay un enorme interés en averiguar si la concentración de este compuesto es variable a lo largo del año de Venus, o si es diferente en diversas regiones del planeta. Dada su baja concentración, no todas estas preguntas podrán ser respondidas con los medios actuales y añadirán un nuevo motor para el desarrollo técnico que requiere la ciencia.

¿Hemos encontrado una “huella de la vida”?

Hay una serie de cuestiones más profundas que afectan a las propias premisas del estudio. La gran pregunta que subyace es la siguiente: ¿es realmente el fosfano una “huella de la vida”?

Hace un año se presentó convincentemente el papel del fosfano como biomarcador por su imposibilidad de ser creado por medios no artificiales en las condiciones de los planetas rocosos. Desde la biología aún debemos profundizar cómo determinados microorganismos anaeróbicos generan este compuesto y si podrían soportar las durísimas condiciones ambientales de Venus, aun rebajadas a los niveles atmosféricos donde se situarían.

Los organismos vivos también fueron propuestos en el pasado para explicar algunas de las estructuras que vemos en el espectro ultravioleta de Venus, de una manera mucho más aventurada que la que nos ocupa. ¿Podrían ambas hipótesis estar conectadas de alguna manera? Solo la biología podrá responder a estas preguntas.

Lo que nos queda por comprender sobre la atmósfera de Venus

En el terreno de la química atmosférica los interrogantes también se multiplican.

Aunque el fosfano se halla presente en Júpiter y Saturno, los gigantes gaseosos son capaces de generarlo gracias a dos ingredientes de los que Venus carece: una enorme cantidad de hidrógeno (prácticamente la totalidad de sus atmósferas) y una presión atmosférica descomunal debido a su también gigantesca masa.

Estos ingredientes no los encontramos en los planetas rocosos, incluso a pesar de que Venus no es como la Tierra en cuanto a presión y temperatura. Aunque los autores del descubrimiento buscaron con ahínco mecanismos alternativos, tuvieron que descartarlos todos. Sin embargo, es justo decir que las incógnitas acerca de los procesos químicos que operan en el planeta todavía son demasiado numerosas como para pasarlas por alto.

No comprendemos bien la química de la atmósfera de Venus. Es precisamente en este campo donde cabe esperar un debate más interesante en los próximos meses.

Un empujón para la misión DAVINCI+

Muchas de estas preguntas no se podrán responder con la información de la que disponemos ahora mismo. Probablemente tampoco con la misión Akatsuki de la Agencia Japonesa de Exploración Aeroespacial, que actualmente orbita en torno al planeta, ni con las misiones propuestas EnVision (ESA) ni VERITAS (NASA), porque todas ellas observan el planeta desde fuera.

Necesitamos una nave capaz de atravesar la densa atmósfera de Venus y darnos información de calidad sobre los niveles más profundos. Es la idea de DAVINCI+, una de las misiones preseleccionadas por NASA dentro de su programa Discovery, y pendiente de la decisión final que tomarán el próximo verano.

De llevarse a cabo, sería capaz de ofrecernos un recorrido por la evolución atmosférica de nuestro vecino, desde su pasado potencialmente habitable y húmedo hasta el infierno en el que el efecto invernadero lo ha convertido. El hallazgo de fosfano da un fuerte impulso para su confirmación al poner encima de la mesa una posibilidad que, hasta la fecha, pocos tomaban en serio.

El avance de la ciencia, aunque esté salpicado de sobresaltos y retrocesos, es continuo e imparable. Hemos sido testigos en los últimos días de un anuncio inesperado, bien fundamentado en los hechos pero todavía rodeado de numerosas incógnitas. A partir de aquí, veremos emerger un árbol de investigaciones científicas que nos llevarán en una dirección o en otra pero que, en todo caso, nos harán mucho más sabios por el camino.

Sobre el autor: Santiago Pérez Hoyos es investigador doctor permanente – Astronomía y Astrofísica, Universidad del País Vasco / Euskal Herriko Unibertsitatea

Este artículo fue publicado originalmente en The Conversation. Artículo original.

El artículo ¿Qué hacemos ahora con Venus? se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Una electrónica para Venus
2. NASA, ¿cuándo vas a llevarnos a Venus en un barco (o en lo que sea)?
3. Sorpresas en la atmósfera del polo sur de Venus

“Vampiro. 1. Espectro o cadáver que, según cree el vulgo en algunos países, va por las noches a chupar poco a poco la sangre de los vivos hasta matarlos.

2. Murciélago hematófago de América del Sur.”

Diccionario de la Lengua.

“Si hay una historia bien documentada en el mundo, es la de los vampiros. No falta nada: interrogatorios, certificaciones de notables, de cirujanos, de sacerdotes de la parroquia, de magistrados. La prueba judicial es una de las más completas. Y con todo eso, ¿quién cree en los vampiros? ¿Estaremos todos condenados por no haber creído?

Jean-Jacques Rousseau, Carta a Christopher de Beaumont, 1762.

“Los vampiros les causan a menudo grandes sufrimientos, mordiéndoles en la cruz, no tanto a causa de la pérdida de sangre que resulta de la mordedura, como a causa de la inflamación que luego produce el roce de la silla. Sé que en Inglaterra han puesto en duda últimamente la veracidad de este hecho; por tanto, es una buena suerte el haber estado yo presente un día en que se cogió a uno de esos vampiros (Desmodus d’Orbigny, Wat.), en el mismo dorso de un caballo. Vivaqueábamos muy tarde una noche cerca de Coquinho, en Chile, cuando mi criado, advirtiendo que un caballo de los nuestros estaba muy agitado, fue a ver qué ocurría; creyendo distinguir algo encima del lomo del caballo, acercó con rapidez una mano y cogió un vampiro. A la mañana siguiente, la hinchazón y los coágulos de sangre permitían ver dónde había sido mordido el caballo; tres días después hicimos uso de éste, sin que pareciera resentirse ya de la mordedura.”

Charles Darwin, Viaje de un naturalista alrededor del mundo, 1839.

Contaba Anthony Masters en su libro sobre vampiros, publicado en 1974, que hay dos tipos de vampiro, el mítico y el real, y ambos, según cuenta, pueden matar y son asesinos. El mítico, cuenta la leyenda, mata personas por miles, incluso solo por el terror que provoca. En su tiempo, y quizá ahora, era juzgado, condenado y ejecutado por asesino psicópata o, si no era así, simplemente era linchado. El vampiro real ataca para alimentarse y se le tiene por cruel y estremecedor.

Foto: Clément Falize / Unsplash

La mitología del vampiro, de ese vampiro mítico, no el real, aparece en muchas culturas y religiones de todo el mundo, tal como detalla Anthony Masters. La definición de vampiro y de vampirismo varía según el origen de la leyenda. En la mitología, los vampiros son seres no muertos, inmortales por tanto, y misteriosos y nocturnos. Ocupan la frontera, que atraviesan si les apetece, entre el mundo de los vivos y el de los muertos. El grupo de K. Gubb, del Hospital Box-Hill de Melbourne, en Australia, escribe que los vampiros son criaturas poderosas que provocan miedo, intrigan y fascinan, y dominan a otras personas. Se hicieron famosos y conocidos con los escritos de John Polidori y Bram Stoker en el siglo XIX.

En la revisión sobre vampirismo, que publicaron en 2013, Lennon da Costa Santos y sus colegas, de la Universidad Federal de Minas Gerais, en Brasil, proponen que se cree en la existencia de los vampiros cuando, en alguna persona, se observan síntomas de algunas enfermedades que recuerdan la descripción del aspecto de los vampiros de las leyendas. Mencionan la porfiria, que provoca un semblante anémico con una palidez exagerada. Es una enfermedad causada por un defecto metabólico que impide la síntesis de la hemoglobina de la sangre y, como efectos, hay anemia y palidez. La síntesis de la hemoglobina se detiene un paso anterior, cuando se produce la porfirina, molécula que precede a la hemoglobina, que, por tanto, se acumula en los tejidos del paciente, sobre todo en la zona subcutánea, los huesos y los dientes.

Además, la porfirina reacciona a la luz y produce radicales de oxígeno que, al sol, pueden provocar heridas en la piel. De ello la leyenda sobre la aversión al sol de los vampiros que, incluso, los puede destruir, y su obligada vida nocturna. La porfirina, en casos graves, llega a deformar el rostro, retrae los labios y muestra la dentadura que, así, parece más grande de lo habitual. Son los afilados colmillos del vampiro. Los enfermos de porfiria desarrollan conductas antisociales, agresividad y aislamiento, incluso desórdenes mentales. Para la imaginación popular, son seres malditos o demonios encarnados.

Vampiro (1895) de Edvard Munch

Los autores aluden al Doctor Juan Gómez Alonso que, en su tesis, defendida en 1992, y en publicaciones posteriores, relaciona el vampirismo popular con la rabia y menciona la coincidencia de una epidemia de esta enfermedad en Hungría, a principios del siglo XVIII, con la difusión de leyendas sobre vampiros en áreas montañosas y remotas de los Cárpatos. Gómez Alonso comenta que el vampirismo, según el mito, se transmite por mordedura, como muchas enfermedades transmitidas por animales y, entre ellas, la rabia. Además, el vampiro se puede transformar a voluntad en lobo, perro o murciélago, animales todos ellos que pueden contagiar de la rabia.

Es una enfermedad que altera la conducta, provoca más agresividad, y actúa en áreas cerebrales del sistema límbico, como el hipotálamo o la amígdala, encargadas de sentimientos y emociones. Lleva a conductas nocturnas, como la leyenda dice de los vampiros. Hay otros síntomas de la rabia que recuerdan a los relatos de vampiros: espasmos musculares, gruñidos, hidrofobia, fotofobia o, incluso, evitar la propia imagen en el espejo.

En conclusión, para Gómez Alonso, las epidemias de rabia del siglo XVIII pudieron ampliar y difundir los mitos sobre vampiros, ya existentes, en Europa centra y oriental.

Una tercera enfermedad a la que se atribuye la leyenda sobre los vampiros es la pelagra, provocada por la deficiencia en vitamina B3 o niacina que, en el siglo XVIII, en la época de la difusión de las leyendas sobre vampiros, se atribuye a la extensión del cultivo del maíz, que llegó a Europa desde América y, poco a poco, por su fácil cultivo y rendimiento, se convirtió en la base de la alimentación de las clases más pobres. La falta de vitamina B3 en el maíz provocó la deficiencia en esta vitamina en quienes lo tenían como el alimento más consumido.

Según la hipótesis de Jeffrey Hampl y William Hampl III, de las universidades de Massachusetts y de Rhode Island, la pelagra provoca dermatitis y demencia, con insomnio e irritabilidad, y, además, hipersensibilidad a la luz que les provoca alteraciones en la piel y quemaduras. Se inflaman los labios y los dientes parecen más grandes. Todos ellos son síntomas que también describen a los vampiros.

En psiquiatría, el vampirismo clínico se define como una creencia en fantasmas chupadores de sangre o que intentan conseguir sangre pues les produce un profundo placer sexual. Otros autores, según Gubb, consideran que el vampirismo clínico es el acto concreto de beber sangre de la víctima, una conducta poco común que se asocia con la esquizofrenia. Y hay expertos que asocian el vampirismo con actos agresivos o sexuales con cadáveres o con moribundos. Incluso se han descrito pacientes con autovampirismo cuando el sujeto bebe su propia sangre.

Uno de los vampiros más famosos del último siglo fue Peter Kürten, conocido como el Vampiro de Dusseldorf, nacido en 1893, asesinó, según la sentencia que le condenó, a nueve personas, con más intentos frustrados y más de ochenta agresiones sexuales. Murió guillotinado en 1931, a los 48 años, y la leyenda cuenta que preguntó, poco antes de la ejecución, si, una vez cortada la cabeza, oiría, aunque fueran unos segundos, la sangre saliendo de su cuerpo. En el juicio relató su pasión por beber la sangre de sus víctimas, en un síndrome llamado hematodipsia.

A pesar de la popularidad del vampirismo, las publicaciones científicas sobre este síndrome son escasas, sobre todo a partir de 1940, lo que indica la escasa investigación sobre ello. El grupo de Gubb llega a esta conclusión después de comentar trabajos publicados en Sudáfrica, Francia, Suiza y Estados Unidos hasta 2006.

Un vampiro común (Desmodus rotundus) alimentándose de un cerdo (animales disecados expuestos en el Museo de Historia Natural de Viena). Foto: Sandstein /Wikimedia Commons

Después de repasar el mito vamos a conocer la realidad del vampiro. Son murciélagos con una dieta exclusivamente de sangre. Son los únicos mamíferos con alimentación hematófaga o, si se quiere, sanguívora aunque sea una palabra que no está en el Diccionario. Solo hay tres especies de murciélagos con dieta de sangre: el vampiro común, Desmodus rotundus, que ya conocía Darwin; el vampiro de piernas peludas, o Dyphylla ecaudata, y el vampiro de alas blancas o Diaemus youngi, que solo gusta de la sangre de aves. Las tres especies se encuentran en Centro y Sudamérica, desde México hasta Chile y Argentina.

Las tres especies pertenecen a la misma familia aunque a distintos géneros, y se supone que han tenido un antepasado común. En esa familia hay murciélagos con dietas muy variadas como, por ejemplo, se alimentan con néctar, polen, insectos, frutas, pescado y carne. Y, como sabemos, solo tres especies tienen dieta de sangre, unos 10 mililitros al día. Al morder, segregan un anticoagulante que es una proteína muy apropiadamente llamada draculina. Horas después de la mordedura, la herida sigue sangrando con suavidad. Por cierto, rara vez muerden a una persona y, si lo hacen, es en las extremidades, los dedos o la nariz.

Es una dieta poco habitual y supone adaptaciones para que sea funcional y eficaz: mucho líquido y, por tanto, un potente sistema renal para eliminarlo, y una gran vejiga para almacenar la orina; riesgo, si no se controla y elimina el exceso de hierro, de provocar síntomas de toxicidad; además, es una dieta con exceso de proteínas y pocos carbohidratos y vitaminas; fuertes caninos para morder; sistema sensorial para detectar, por medio de infrarrojos, las zonas calientes de la piel de la víctima como las áreas con más cercanía del sistema circulatorio y de la sangre y allí, morder,…

El estudio del genoma del vampiro común, Desmodus rotundus, del grupo de Lisardia Zepeda, de la Universidad de Copenhague, ha localizado algunas de las adaptaciones a la dieta de sangre. Tienen vías de síntesis de vitamina B, que es muy escasa en la sangre y necesitan elaborarla. Hay proteínas en el intestino del vampiro que, con agua y dióxido de carbono, abundantes en la sangre, sintetizan hidratos de carbono. El exceso de hierro en la sangre se controla por genes que dirigen su eliminación. Las proteínas de la sangre se metabolizan y los productos resultantes se eliminan por el sistema renal en la orina.

Estos autores también han localizado los genes que dirigen la detección de radiación infrarroja, es decir, de calor, para encontrar en la piel las zonas con más circulación de sangre y, así, elegir el lugar para morder.

Estas adaptaciones, según el estudio publicado por el grupo de Fidel Botero Castro, de la Universidad de Montpellier, sobre el ADN de las mitocondrias, revelan que se habían seleccionado hace unos 4 millones de años, con una relativa rapidez para lo que duran estos procesos.

Referencias:

Botero Castro, F. et al. 2018. In cold blood: Compositional bias and positive selection drive the high evolutionary rate of vampire bats mitocondrial genomes. Genome Biology and Evolution 10: 2218-2239.

Gómez, J.A. 1998. Rabies: a posible explanation for vampire legend. Neurology 51: 856-859.

Gubb, K. et al. 2006. Clinical vampirism: a review and illustrative case report. South African Psychiatry 9: 163-168.

Hampl, J.S. & W.S. Hampl III. 1997. Pellagra and the origin of a myth: evidence from European literatura and folklore. Journal of the Royal Society of Medicine 90: 636-639.

Masters, A. 1974. Historia natural de los vampiros. Ed. Bruguera. Barcelona. 318 pp.

Santos, L.C.S. et al. Medical explanations for the myth of vampirism. Revista Medica de Minas Gerais 23: 510-514.

Velasco, E. 2018. Descubren cómo los vampiros pasaron a alimentarse solo de sangre. La Vanguardia 20 enero.

Wikipedia. 2018. Vampire bat. 29 October.

Wikipedia. 2020. Peter Kürten. September 4.

Zepeda Mendoza, M.L. et al. 2018. Hologenomic adaptations underlying the evolution of sanguivory in the common vampire bat. Nature Ecology & Evolution doi: 10.1038/s41559-018-0476-8

Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.

El artículo Los vampiros se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. A tomar el sol
2. El caso de Julius Lederer (y del agua que bebemos)
3. Un paseo por la ciudad

Aunque un experimento te lo cuente cualquier libro de texto no quiere decir que como te lo cuentan sea correcto. Por eso es tan importante reproducir los experimentos. El caso de Arquímedes y la corona ilustra el argumento. Da la charla César Tomé López, editor de este Cuaderno de Cultura Científica, de Mapping Ignorance y responsable de proyección internacional de Euskampus Fundazioa.

La conferencia se impartió dentro del marco del festival Passion for Knowledge 2019 (P4K) organizado por el Donostia International Physics Center (DIPC).



Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus

El artículo César Tomé López – Naukas P4K 2019: ¿Eureka?¿En serio? se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. José Miguel Viñas – Naukas P4K 2019: De nubes las pinacotecas están llenas
2. Joaquín Sevilla – Naukas P4K 2019: Lo que esconden unos champiñones al ajillo
3. Ambrosio Liceaga – Naukas P4K 2019: Nunca quisimos coches voladores

El sistema nervioso está formado por neuronas y células gliales. De estas últimas, las más abundantes son los astrocitos, que, entre otras muchas funciones, se encargan de captar la glucosa del torrente sanguíneo para proporcionar energía y permitir la actividad neuronal necesaria, y así asegurar que las funciones cognitivas se ejecuten de una manera correcta. Los receptores cannabinoides tipo 1 (CB1), que modulan la comunicación entre los astrocitos y las neuronas, constituyen la principal diana del componente psicoactivo del cannabis, llamado delta-9-tetrahidrocannabinol (THC).

¿Qué pasa cuando el THC actúa sobre los astrocitos? La investigación, en la que ha participado el grupo del doctor Pedro Grandes del Departamento de Neurociencias de la Facultad de Medicina y Enfermería de la UPV/EHU, concluye que la activación de los receptores de cannabinoides CB1 en las mitocondrias (orgánulos celulares encargados de la producción de energía) de los astrocitos de ratón impide el metabolismo de la glucosa y la producción de lactato en el cerebro, lo cual altera la función neuronal, causando un deterioro de las conductas de interacción social.

Según el Dr. Grandes, “la activación de estos receptores conduce a que los astrocitos generen una menor cantidad de especies reactivas de oxígeno, lo que afecta negativamente a la producción glucolítica de lactato causando un estrés neuronal y una falta de interacción social. La importancia de esta investigación radica no sólo en la identificación de este déficit que puede revertirse mediante la manipulación genética y farmacológica de estos cambios moleculares y bioquímicos causados por el tratamiento cannabinoide, sino también por lo que aporta al conocimiento de las alteraciones causadas por el cannabis en el cerebro”.

La colaboración del grupo de investigación del Dr. Pedro Grandes con el equipo del Dr. Giovanni Marsicano, de la Universidad de Burdeos, resultó fundamental hace unos años para demostrar por primera vez la presencia de receptores CB1 en las mitocondrias de las neuronas, cuya activación reduce la actividad mitocondrial causando pérdida de memoria. Los resultados de estos estudios se publicaron en el año 2012 en Nature Neuroscience y en 2016 en Nature. Sin embargo, “quedaba pendiente conocer cuál era la función de los receptores CB1 localizados en mitocondrias de astrocitos, de ahí la relevancia de este nuevo hallazgo, que además supone una continuidad en la línea de investigación y cooperación transfronteriza”, explica el doctor Grandes. Este descubrimiento se ha publicado en Nature.

Referencias:

Jimenez-Blasco D, Busquets-Garcia A, Hebert-Chatelain E, Serrat R, Vicente-Gutierrez C, Ioannidou C, Gómez-Sotres P, Lopez-Fabuel I, Resch-Beusher M, Resel E, Arnouil D, Saraswat D, Varilh M, Cannich A, Julio-Kalajzic F, Bonilla-Del Río I, Almeida A, Puente N, Achicallende S, Lopez-Rodriguez ML, Jollé C, Déglon N, Pellerin L, Josephine C, Bonvento G, Panatier A, Lutz B, Piazza PV, Guzmán M, Bellocchio L, Bouzier-Sore AK, Grandes P, Bolaños JP, Marsicano G. (2020) Glucose metabolism links astroglial mitochondria to cannabinoid effects Nature doi: 10.1038/s41586-020-2470-y

Magistretti, P.J. (2020) How lactate links cannabis to social behaviour Nature (News & Views) 583, 526-527 doi: 10.1038/d41586-020-01975-5

Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa

El artículo El cannabis rompe el equilibrio metabólico entre neuronas y astrocitos alterando el comportamiento social se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. El límite entre la vida y la muerte en las neuronas
2. Un nexo cannabinoide entre mitocondrias y memoria
3. El citoesqueleto de las neuronas y el alzhéimer

Concha trompeta de Chipícuaro. Arte tolteca (años 300-900). Fuente: Smithsonian Institution

 

Las caracolas han fascinado a los humanos desde siempre. Sus formas intrincadas, sus hermosos colores y patrones, el misterio de su cámara interior capturan la imaginación. Pero además de estas cualidades visuales, tienen un encanto adicional. Gracias a su potente sonido, las caracolas se han utilizado desde la antigüedad en culturas de todo el mundo para atravesar las distancias y el corazón de los dioses. En Nueva Guinea, aún existen llamadas estándar que dan la voz alarma, anuncian una caza exitosa u otros eventos importantes. Sus poderes sobrenaturales fueron conocidos asimismo en Europa. En Bohemia Occidental, se hacía sonar una caracola para ahuyentar a las tormentas. En la India, el shankha es una pieza esencial del budismo y el hinduismo. Constituye un recipiente ritual, así como un instrumento para ocasiones solemnes y ceremonias religiosas. En la mitología hindú, es un emblema sagrado del dios Vishnu. Los monjes tibetanos aún hoy la hacen sonar para convocar a los devotos. Como los niños náufragos de la novela de Golding, los fieles acuden a su llamada limpia y penetrante a través de la distancia.

Quetzalcoatl con la coraza del viento al cuello. Fuente: Wikimedia Commons.

De entre todas estas culturas, la caracola jugó un papel ritual especialmente importante en las sociedades precolombinas de América central y América del sur. Su uso está particularmente bien documentado en la mayoría de las áreas culturales de mesoamérica y en la zona de México occidental, donde se vinculaba a eventos sociales y ceremonias religiosas. Muchos de sus restos se han encontrado en sitios funerarios, indiando su papel como ofrendas1 en diversos ritos de paso. Normalmente, estaban ricamente decoradas, con todo tipo de relieves y pinturas. Cumplían asimismo un papel importante en la guerra, como instrumento de llamada. En algunas sociedades, se asociaban a los rituales y la parafernalia de los chamanes, que ejercían como líderes tanto espirituales y guerreros. De manera más general, la caracola se asociaba como símbolo a Quetzalcoatl, la serpiente emplumada, el dios azteca del viento, el aire y el aprendizaje que siempre llevaba alrededor del cuello la «coraza de viento» o ehecailacocozcatl. Este talismán con forma espiral se fabricaba, precisamente, a paritr de la sección transversal de una caracola y fue usado como collar por gobernantes y sacerdotes.

Una ilustración en el Códice Magliabecchiano muestra a un caracolista (en la cultura azteca eran conocidos como quiquizoani)con su mano introducida dentro de su instrumento (quiquiztli). Podría parecer una forma casual de sujetarlo pero no es el caso. Una de las limitaciones de la concha, es que, a priori, no puede producir más de una nota. Su tono viene dado por su longitud y a priori, este parámetro no es algo que se pueda cambiar. Sin embargo, los caracolistas como Steve Turre, son capaces de afinar varios sonidos introduciendo la mano en el extremo abierto de la caracola. Al hacerlo, el espacio disponible en su interior se vuelve más pequeño, las ondas sonoras se acortan y el resultado es un sonido sensiblemente más agudo que el original. El efecto es el mismo que cuando alguien vierte agua dentro una botella para cambiar su tono: la mano haría la función del líquido, en este caso. Hoy en día, los intérpretes de trompa utilizan esta misma técnica de afinación “manual” para afinar ciertas notas. Este instrumento de viento metal hermosamente acaracolado, tiene de hecho un origen muy similar al de la concha. Las versiones primitivas de la trompa consistían sencillamente en cuernos de animales encontrados (en inglés su nombre todavía es horn, de hecho), que fueron ganando complejidad hasta adquirir su actual forma metálica. Sin embargo, el recurso de afinar con la mano no fue explotado en Europa hasta el siglo XVIII. La ilustración del Códice Magliabecchiano sugiere que ya era utilizado por los intérpretes de conchas aztecas al menos desde dos siglos antes.

Códice Magliabecchiano, XIII, 11, 3. Xochipilli, “noble flor”, dios del sol naciente, las flores y la alegría, es llevado en una litera adornada con mazorcas. Códice Magliabechiano, f. 35r. Reprografía: Marco Antonio Pacheco / Raíces. Fuente: Wikimedia Commons

 

Curiosamente, la vinculación de las conchas con las culturas de centroamérica ha traído de vuelta este instrumento al mundo de las orquestas. Muchos compositores contemporáneos, especialmente en ese lindísimo país llamado México, han utilizado su característico sonido para evocar los ecos del pasado de su nación. Recuerdo la primera vez que yo escuché el penetrante tono de una caracola, brillante, tenso y doloroso, llenando la sala Nezahualcóyotl de la Ciudad de México. Sonaba el último movimiento La Noche de los Mayas (20’30’’) de Silvestre Revueltas y el público había hecho suyo aquel concierto. Fue un momento emocionante.

Referencia:

1Novella, Robert. (1991). Shell Trumpets from Western Mexico. Papers from the Institute of Archaeology. 2. 42. 10.5334/pia.16.

Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica

El artículo Mayas y aztecas en la orquesta se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. El océano en una caracola
2. Un sonido para hablar con los dioses
3. La caracola más grave del mundo