Cuaderno de Cultura Científica

Foto: Duy Pham / Unsplash

Las relaciones de amistad son mutables; se fortalecen y debilitan con más facilidad de lo que suponemos. De hecho, no es difícil que se desvanezca la relación intensa que une a dos personas para pasar a ser meras conocidas. Aunque hay, no obstante, algunas excepciones a esa regla: las dos o tres amistades que surgen en la juventud temprana y que resisten los estragos que causa el paso del tiempo y la distancia.

Un estudio relativamente reciente, liderado por el británico Robin Dunbar, ha desentrañado algunos aspectos de las relaciones sociales de chicos y chicas, y los avatares que sufren durante un periodo de 18 meses que comprende el final de los estudios de bachillerato y el comienzo de los universitarios. El estudio reveló, por ejemplo, que el 40% de las personas de la red social de los y las estudiantes se renovó durante el tiempo en que se prolongó; ese porcentaje refleja la fluidez de las relaciones sociales en ese segmento de edad. Lo que sorprendió al equipo de investigación es que normalmente las nuevas relaciones venían a ocupar el lugar de las que se perdían dentro de la red social. Esto es, mantenían con las nuevas amistades la misma frecuencia de contactos que con las que habían sido sustituidas. Cada persona tenía, en ese sentido, una huella social característica.

Para la amistad, conversaciones y actividades

Por otro lado, lo que más contribuía a que las chicas mantuviesen las amistades anteriores a la universidad eran las conversaciones, cara a cara o por teléfono. En los chicos, sin embargo, las conversaciones no afectaban en medida alguna a la probabilidad de mantener una amistad. Lo que influía eran las actividades que se hacían con las otras personas, como ir de bares, practicar algún deporte, ir al monte u otras. No es que la práctica de estas actividades no ayudase también a las chicas a mantener sus relaciones; lo hacía, pero afectaban en menor medida. Otra diferencia entre chicos y chicas era el tiempo que duraban las llamadas de teléfono y su distribución a lo largo de las horas. Las de las chicas, en promedio, duraban 150 s por la mañana, pero llegaban a los 500 s hacia el final del día. Las de los chicos, sin embargo, eran del orden de 100 s y no había diferencia entre la mañana y la noche.

Aunque en el estudio observaron grandes diferencias en los hábitos horarios de las personas monitorizadas, resultó que esos hábitos no se modificaron durante los 18 meses del estudio. Quienes madrugaban al comienzo lo siguieron haciendo al final, y lo mismo ocurrió con quienes trasnochaban.  En un estudio diferente, hecho con 1000 estudiantes universitarios daneses, comprobaron que un 20% madrugaban, otro 20% trasnochaban y todos los demás no tenían una tendencia horaria marcada. También descubrieron que quienes madrugaban no tenían preferencia por amistades con sus mismos hábitos, aunque quienes trasnochaban sí tendían a tenerlas. Los trasnochadores tenían redes sociales más amplias que los madrugadores (35 vs. 28), aunque, quizás lógicamente, estos dedicaban más tiempo a cada llamada telefónica (112 s vs. 94s.). Las redes de los madrugadores eran más sólidas, de hecho, más estables.

A juicio de Dunbar, el dato más inesperado y revelador de la naturaleza de nuestras relaciones sociales fue el de la constancia en su estructura, a despecho, incluso, de la identidad concreta de quienes la conforman. Queremos que nuestras amistades sean personas agradables, en quienes poder confiar; queremos congeniar con ellas. Pero lo que de verdad importa no es tanto quiénes forman nuestro grupo de amigos, cuanto el simple hecho de tenerlos.

Fuente: Robin Dunbar (2021): Friendship-ology. New Scientist 249 (3324): 36-40.

Para saber más:

Nos relacionamos con ciento cincuenta personas
Familiares, amigos, amigas y personas conocidas

Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU

El artículo En la amistad no importa tanto quien sino que lo sea se ha escrito en Cuaderno de Cultura Científica.

¿Estamos realmente diseñados para conectar con los demás? Si es así, ¿por qué siguen existiendo los psicópatas? ¿Se pueden tratar trastornos delirantes como la paranoia desde el punto de vista de la evolución? O ¿cómo ha cambiado la atracción sexual desde la época de nuestros ‘abuelos’ homínidos hasta ahora?

A estas y otras cuestiones relativas a la evolución del comportamiento humano se trató de dar respuesta durante la IV Jornada Nacional de Evolución y Neurociencias, evento organizado por la Cátedra de Cultura Científica de la UPV/EHU y la Red de Salud Mental de Bizkaia, que tuvo lugar los días 28 y 29 de abril en el Bizkaia Aretoa – UPV/EHU de Bilbao.

Desde que en 2017 un grupo de psiquiatras de la Red de Salud Mental de Bizkaia organizara la primera edición de esta jornada, la cita se ha convertido en un punto de encuentro para profesionales de distintos ámbitos científicos como la psiquiatría, la psicología, la biología o la filosofía con un interés común: la conducta humana desde una perspectiva evolucionista y su divulgación científica en un formato accesible y ameno para todos los públicos, a la par que riguroso y actualizado.

La interrelación entre ejercicio, biología, encéfalo y ecología es un bucle que se retroalimenta. Fernando Valladares, biólogo y profesor de investigación del CSIC, donde dirige el grupo de Ecologia y Cambio Global en el Museo Nacional de Ciencias Naturales, nos lo explica magníficamente en esta charla. Muy recomendable su web.



Para saber más:

Envejecer sanamente gracias al ejercicio físico
Memoria y envejecimiento: los efectos beneficiosos del ejercicio físico son tremendamente volátiles
Respuesta de los sistemas respiratorio y cardiovascular al ejercicio físico

Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus

El artículo IV Jornada Nacional de Evolución y Neurociencias: Fernando Valladares – Del ejercicio a la ecología y viceversa se ha escrito en Cuaderno de Cultura Científica.

Imagen de microscopia electrónica de transmisión de una bacteria magnetotáctica, Magnetovibrio blakemorei, con los nanoimanes que sintetiza en su interior. Foto: Grupo de Magnetismo y Materiales Magnéticos de la UPV/EHU

Imaginemos un vehículo diminuto, un nanocoche (de dimensiones un millón de veces inferiores al milímetro), dotado de una estructura magnética que permita controlarlo y dirigirlo mediante campos magnéticos. Imaginemos que introducimos ese coche en el cuerpo humano y lo llevamos hasta el lugar preciso en el que se necesite liberar un medicamento o eliminar células cancerosas. En esta audaz idea trabajan numerosos científicos repartidos por todo el mundo, entre ellos el grupo multidisciplinar Magnetismo y Materiales Magnéticos (GMMM) de la Universidad del País Vasco. Este equipo participa en una investigación para conseguir materializarla.

En concreto, este grupo, liderado por la profesora de la Facultad de Ciencia y Tecnología Maria Luisa Fernández-Gubieda, explora el uso de bacterias magnéticas, conocidas como bacterias magnetotácticas, en la lucha contra el cáncer. Estos microorganismos tienen la sorprendente habilidad de formar nanopartículas magnéticas de óxido de hierro dentro de sus células. Las partículas, con diámetros de unos 50 nanómetros (100 veces más pequeñas que las células de la sangre), se organizan, dentro de la bacteria, en forma de cadena, que actúa como una brújula magnética y orienta la bacteria en su conjunto en la dirección definida por un campo magnético. La idea sería utilizarlas para tratar el cáncer mediante hipertermia magnética o transporte de medicamentos: dirigirían las bacterias al lugar donde se localiza el tumor, y se calentarían por campos externos para conseguir quemar las células cancerosas y/o liberar fármacos mediante calor u otro estímulo externo.

“La bacteria es un excelente modelo magnético que nos ayuda a entender el comportamiento de las nanopartículas magnéticas y desarrollar modelos que transcienden a otros sistemas”, explica Mª Luisa Fernández-Gubieda.

Propiedades de las bacterias magnéticas

Ahora, en colaboración con un equipo del Helmholtz Zentrum Berlin, liderado por Sergio Valencia, han podido explorar más al detalle las propiedades magnéticas de estas bacterias. El grado de éxito de todas las posibles aplicaciones depende de las propiedades magnéticas de estas bacterias, y en concreto de cada uno de los nanoimanes que conforman sus cadenas. Sin embargo, la señal magnética de una única partícula es tan débil que, hasta ahora, era necesario estudiar la respuesta de promedios de cientos o miles de nanopartículas para obtener resultados significativos.

Contar solo con esos valores promediados restringía el diseño de aplicaciones personalizadas de nanoimanes. Y esto es lo que ahora ha cambiado. La física Lourdes Marcano, miembro de GMMMT, ha desarrollado un nuevo método. “Ahora podemos obtener información precisa sobre las propiedades magnéticas de varios nanoimanes individuales de manera simultánea», dice.

Anisotropía magnética

Efectivamente, el nuevo método permite medir las propiedades magnéticas de las nanoestructuras magnéticas individuales, incluso cuando están en el interior de entidades biológicas. En concreto, gracias a las imágenes magnéticas obtenidas en el microscopio de transmisión de rayos X del sincrotrón BESSY II (Helmholtz Zentrum Berlin), y con la ayuda de simulaciones teóricas, han conseguido información precisa sobre la anisotropía magnética de cada nanopartícula dentro del campo de visión del microscopio. La anisotropía magnética describe cómo reacciona una nanopartícula magnética a los campos magnéticos externos aplicados en una dirección arbitraria. Es, por tanto, un parámetro importante para controlar y dirigir las nanopartículas magnéticas.

De momento, obtener imágenes magnéticas de nanopartículas magnéticas dentro de una célula biológica con suficiente resolución solo es posible en grandes instalaciones de radiación sincrotrón, como la de del Helmholtz Zentrum Berlin. “Sin embargo, en el futuro, con el desarrollo de fuentes compactas de rayos X de plasma, este método podría convertirse en una técnica estándar de laboratorio», afirma Sergio Valencia.

Referencia:

Lourdes Marcano, Iñaki Orue, David Gandia, Lucía Gandarias, Markus Weigand, Radu Marius Abrudan, Ana García-Prieto, Alfredo García-Arribas, Alicia Muela, M. Luisa Fdez-Gubieda & Sergio Valencia (2022) Magnetic Anisotropy of Individual Nanomagnets Embedded in Biological Systems Determined by Axi-asymmetric X-ray Transmission Microscopy ACS Nano doi: 10.1021/acsnano.1c09559

Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa

El artículo Bacterias magnéticas para luchar contra los tumores se ha escrito en Cuaderno de Cultura Científica.

Ya estamos en verano y, para todas aquellas personas que amamos la música en vivo, por fin regresan los conciertos y festivales. Podremos volver a relajarnos, o a soltar adrenalina, dependiendo del estilo de música que escuchemos, mientras vemos tocar a nuestros grupos favoritos. Pero, ¿podremos también aprender algo de Geología a la vez que disfrutamos de los conciertos? Pues la respuesta, como no podía ser de otra manera, es sí.

Existen muchísimos grupos musicales que apelan a las Ciencias de la Tierra, de una manera u otra, en las letras de sus canciones. Y aquí os voy a citar solo algunos ejemplos del estilo musical que más me gusta, el heavy metal. Como se suele decir, para gustos los colores y, en este caso, si me permitís la broma, a mí me gusta el negro.

A veces los detalles geológicos son muy sutiles y se esconden como una simple frase dentro de una estrofa en la que parece que no viene a cuento, como en la canción “Hard as Iron” de Judas Priest, donde dicen, de repente:

“Terremoto, rompe la escala de Richter”

Creo que nunca una frase de una canción ha dado para tantas acaloradas discusiones geológicas como esta mención a una escala de medida sísmica ya obsoleta.

En otras ocasiones hay que leer un poco entre líneas para detectar la información geológica contenida en una canción. Un ejemplo lo encontramos en una estrofa de la canción “Ice Queen” del grupo Within Temptation:

“Con sus alas frías ella se acerca

Será mejor que sigas corriendo

Por calor, pronto estarás rogando

Vamos, solo siéntelo

Ella cubre la tierra con su letal manto”

Sí, están hablando, de manera metafórica, de glaciaciones.

Aunque lo habitual es que los grupos y cantantes nos suelten la información geológica directamente, sin que tengamos que pararnos a pensar mucho en lo que nos están diciendo. Así, Marko Hietala tiene una canción titulada “Stones” en la que, lógicamente, habla de piedras. Fijaos en lo que dice el estribillo:

“¡Piedras! Cayendo del cielo

¡Más piedras! Creciendo en el suelo

¡Piedras! Viajando por las estrellas

¡Más piedras! Aburridas, ingratas, sin vida

Piedras…”

O como olvidar al grupo Siniestro Total con su mítico tema “Pueblos del mundo extinguíos”, que inician la primera estrofa con fuerza:

“Ya no hay trilobites en el mar

En Siberia no queda ni un mamut”

Por si nos habíamos quedado con ganas de más, en la segunda estrofa nos dejan claro que el patrimonio fósil debe conservarse y exponerse en los museos, aunque emplean su propio toque satírico:

“Sonríe cuando te vayas a fosilizar

Que no piensen luego que lo has pasado mal

Procura extinguirte con clase y dignidad

Piensa en el Museo de Historia Natural”

Si todavía no os he terminado de convencer del enorme papel didáctico en Ciencias de la Tierra del heavy metal, no os preocupéis, porque he dejado los platos fuertes para el final.

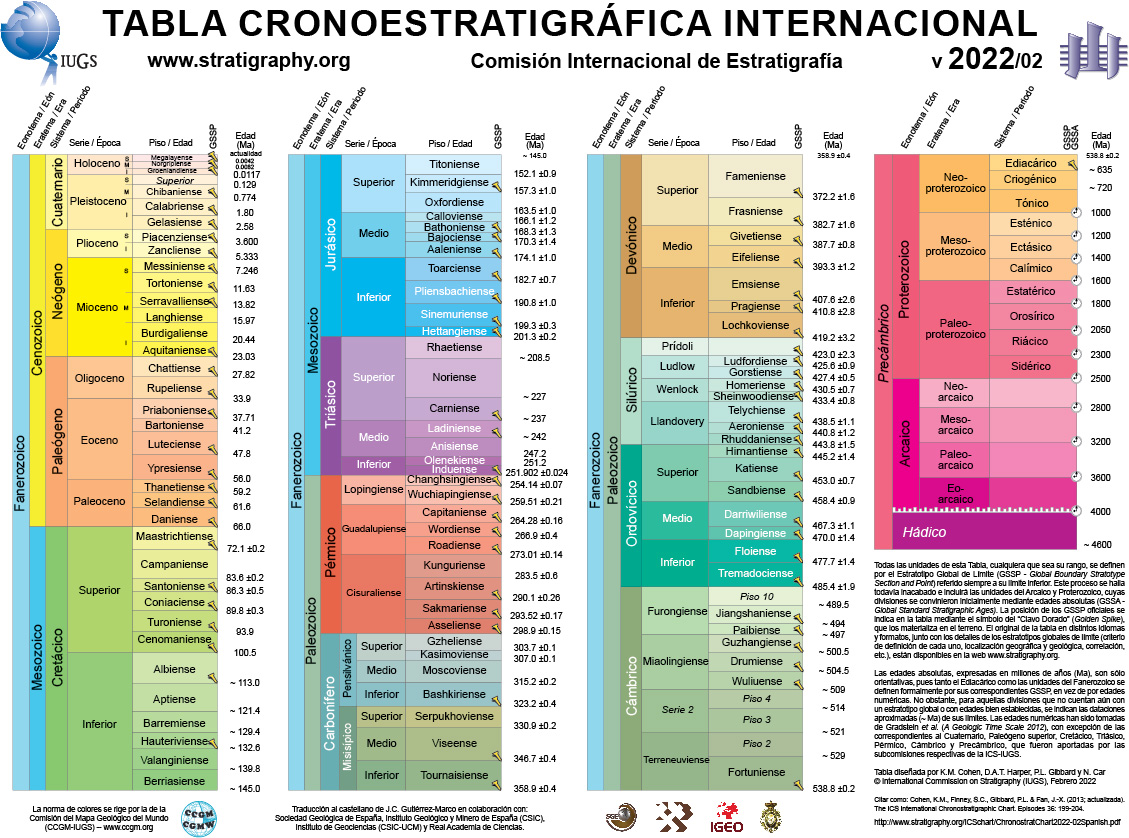Versión más actualizada de la tabla cronoestratigráfica internacional con todas las divisiones de la escala de tiempos geológicos y las edades de sus límites. Imagen tomada de International Comission on Stratigraphy

Seguro que, si este artículo lo lee el profesorado o alumnado de Geología de cualquier nivel educativo y cito la tabla cronoestratigráfica, sabrán lo que es, ya que se la habrán tenido que aprender en algún momento. Para quien no se haya tenido que enfrentar con ella, la tabla cronoestratigráfica es la escala de tiempos geológicos que recoge toda la historia de nuestro planeta. Tiene como unidad básica el millón de años y presenta, de manera ordenada de más antiguo a más moderno, todos los eventos geológicos acontecidos en la Tierra. Tiene diferentes niveles y subdivisiones, siendo los más grandes los Eones, que incluyen varias Eras que se dividen, a su vez, en Periodos y así sucesivamente.

Portadas de los discos del grupo The Ocean “Precambrian”, “Phanerozoic I: Palaeozoic” y “Phanerozoic II: Mesozoic/Cenozoic”, este último con el material promocional asociado al mismo. Imágenes tomadas de Metalblade

Pues si queréis un truco para memorizarla, únicamente tenéis que aprenderos el título y el orden de las canciones de los álbumes “Precambrian”, “Phanerozoic I: Palaeozoic” y “Phanerozoic II: Mesozoic/Cenozoic” del grupo The Ocean, ya que se llaman como los Periodos geológicos en los que se subdividen estos Eones. Reconozco que las letras son demasiado crípticas y cuesta relacionarlas directamente con los eventos acontecidos en dichos Periodos, pero a veces son muy poco sutiles. Como ocurre en la canción titulada “Permian: The Great Dying”, en donde aluden a conceptos tales como Laurasia o Gondwana, citan al aumento del nivel del mar como comienzo de la Gran Mortandad, se preguntan si estaremos entre el 5% superviviente y ya avisan de que harán falta 30 millones de años para recuperarse.

Si os interesa más la Geología Planetaria y queréis saber las principales características definitorias de los planetas de nuestro Sistema Solar, el grupo Nanowar of Steel nos hace un fantástico resumen en su tema “Uranus”. Tendría que transcribiros la letra entera para hacerles justicia, porque es una delicia geológica que, además, mezclan con la historia del descubrimiento de este planeta, así que os animo a ver el videoclip oficial. Eso sí, os aviso de que este grupo es del estilo “heavy metal de broma”, por lo que os echaréis unas buenas risas.

Portada del disco “Endless forms most beautiful” del grupo Nightwish y parte de su material promocional. Imágenes tomadas de Nightwish

Pero si un grupo musical merece una atención especial, ese es Nightwish. En 2015 sacaron un disco titulado “Endless forms most beautiful” en homenaje a una frase escrita por Charles Darwin en su libro “On the Origin of Species”. Todas y cada de las canciones es pura geología, aunque algunas la tienen escondida detrás de metáforas y símiles. Pero aquí solo voy a aludir a dos de ellas.

La canción que da título al disco, “Endless forms most beautiful”, hace un pequeño recorrido por algunos de los eventos evolutivos más importantes de la historia de nuestro planeta, incluyendo palabras tales como Panthalassa, Tiktaalik o eucariota. Pero si la letra es una delicia geológica, el videoclip oficial es una fantástica metáfora alusiva al motor que mueve la evolución biológica desde el origen de la vida en la Tierra. Pero… tiene una pequeña licencia artística y es que hace pequeños saltos en el tiempo, no continúa la historia de manera lineal desde más antiguo a más moderno.

Aunque este problemilla lo solventan en la canción “The Greatest Show on Earth”. Se trata de un tema de más de 20 minutos de duración que recoge los 4600 millones de años de historia de nuestro planeta dividida en tres actos, con dos partes adicionales en las que el biólogo evolutivo Richard Dawkins cita un pasaje de su libro “The Greatest Show on Earth: The Evidence for Evolution” y el párrafo de “On the Origin of Species” que da título al álbum. Aquí viajamos a un horizonte arcaico, vemos aparecer a LUCA, pasan los Eones hasta que todo termina, dando lugar a un nuevo comienzo en donde Lucy empieza un viaje fuera de África. En esta ocasión, lo que tenéis que ver es el videoclip del concierto que dieron en Wembley en 2015 y fijaros en toda la puesta en escena: asientos, pies de los micrófonos, carteles y vídeos de fondo, además de la letra, claro.

Espero que ahora escuchéis música de otra manera, prestando atención a estos pequeños detalles que nos llenan de cultura geológica sin darnos cuenta. Y también espero que miréis al hard rock y al heavy metal con otros ojos, concretamente con los ojos de la Geología. Obviamente no podía faltar esta analogía en dos estos estilos que, literalmente, se llaman “roca dura” y “metal pesado”, ¿verdad?

Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU

En la misma línea:

¡Música, matemática!

El artículo Heavy metal muy geológico se ha escrito en Cuaderno de Cultura Científica.

 

Desempeñó un papel notablemente modesto pero eficiente como esposa de un gran matemático que llevó a cabo múltiples actividades políticas y sociales, por lo que sus propios logros tendieron a verse eclipsados ​​por su enorme talento matemático. Pero su papel pionero en el campo de la geometría analítica está ahora bien establecido.

Yvette Kosmann-Schwarzbach

Las anteriores palabras de la matemática Yvette Kosmann-Schwarzbach (1941) aluden a la también matemática Marie-Hélène Schwartz, quien fue hija y pareja de dos conocidos matemáticos: el experto en teoría de la probabilidad Paul Lévy (1886-1971) y el especialista en teoría de distribuciones y Medalla Fields en 1950 Laurent Schwartz (1915-2002).

Marie-Hélène Schwartz. Imagen : Images des Mathématiques.

 

Marie-Hélène Lévy nació el 27 de octubre de 1913 en París. Era hija del matemático Paul Lévy y de Suzanne Lévy (1892-1973) —hija del comerciante Paul Lévy (¡su padre y su marido tenían el mismo apellido!) y Berthe Weil, y nieta del filólogo Henri Weil (1817-1913)—. Marie-Hélène era la mayor de la prole del matrimonio Lévy: Denise y Jean Claude eran su hermana y hermano.

Marie-Hélène se educó en París y pasó sus últimos años de estudios de secundaria en el prestigioso lycée Janson de Sailly; allí disfrutaba de las matemáticas y conoció a un estudiante de un curso inferior al suyo, Laurent Schwartz.

Lévy obtuvo buenos resultados en los exámenes de ingreso a las Grandes Écoles y, en 1934, comenzó sus estudios de matemáticas en la École Normale Supérieure de París; era la única mujer en su clase. En abril de 1935, Marie-Hélène y Laurent se comprometieron y planearon casarse en diciembre de ese mismo año.

Una enfermedad cambia sus planes

Los planes de la joven pareja fracasaron: en octubre de 1935 Marie-Hélène enfermó de una tuberculosis pulmonar. Por la gravedad de su dolencia, fue enviada al sanatorio Mont-Blanc en Passy, ​​un centro especializado en enfermedades pulmonares infecciosas crónicas. Allí le auguraron una larga permanencia en el centro, alejada de sus seres queridos. Aunque mejoró poco a poco, los médicos le anunciaron que probablemente no podría casarse y, de hacerlo, debía evitar quedar embarazada porque podría provocarle una recaída.

El 2 de mayo de 1938, nada más abandonar el sanatorio, Marie-Hélène se casó con Laurent Schwartz; aunque, en realidad, ambos se consideraban esposos desde el año 1935 en el que ella fue recluida en el sanatorio.

Marie-Hélène y Laurent Schwartz. Imagen : Images des Mathématiques.

 

El matrimonio se instaló en Laón, ciudad en el departamento de Aisne. Tras graduarse de la École Normale Supérieure de París, Laurent Schwartz había realizado el servicio militar obligatorio y había sido nombrado segundo teniente asignado a Laón. Aunque deseaban tener descendencia, los médicos recomendaron a la pareja esperar cuatro años para evitar una recaída de Marie-Hélène. En el otoño de 1938 se trasladaron a Châtillon-sous-Bagneux cuando Laurent fue destinado a la guarnición de Mont Valérien.

En septiembre de 1939 Laurent terminó su servicio militar y se movilizó inmediatamente cuando estalló la Segunda Guerra Mundial. El 22 de junio de 1940 Francia capituló ante Alemania y, por su seguridad, Marie-Hélène y Laurent —ambos de ascendencia judía— fueron evacuados a Aire-sur-l’Adour antes de que llegaran las tropas nazis a Biscarrosse, donde residía el matrimonio.

Reiniciando los estudios

Laurent fue desmovilizado el 15 de agosto de 1940. El matrimonio viajó brevemente a Toulouse para reunirse con los padres de Laurent; allí conocieron al prestigioso matemático y cofundador del grupo Bourbaki Henri Cartan (1904-2008). Marie-Hélène le pidió consejo sobre cómo podría intentar reiniciar sus estudios académicos; Cartan le recomendó que se mudaran a Clermont-Ferrand, ciudad a la que se había trasladado la Universidad de Estrasburgo tras la invasión alemana. Era una oportunidad tanto para ella como para Laurent. Marie-Hélène comenzó a investigar y publicó su primer artículo en 1941.

En 1942 se cumplían los cuatro años desde que Marie-Hélène había abandonado el sanatorio; la pareja decidió intentar tener esa descendencia tan deseada sin esperar al final de la guerra. Pensaban que la situación en la Francia de Vichy era relativamente estable. Sin embargo, en noviembre de 1942, Alemania ocupó Francia; Marie-Hélène —ya embarazada— y Laurent estaban en peligro extremo, no solo por ser judíos, sino también por ser trotskistas activos. Tuvieron que adoptar identidades falsas —como Marie-Hélène Lengé y Laurent-Marie Sélimartin— y moverse continuamente. Su hijo Marc-André nació el 17 de marzo de 1943.

Tras la invasión aliada de Francia en junio de 1944, Marie-Hélène y su esposo regresaron a París. Después de un año en Grenoble, la familia se mudó a Nancy donde Laurent fue contratado en el otoño de 1945. El 30 de julio de 1947, Marie-Hélène tuvo a su hija Claudine.

La investigación se activa

En el ámbito de las matemáticas Marie-Hélène realizó una investigación sobre un problema propuesto por el especialista en análisis matemático Georges Valiron (1884-1955); recibió útiles sugerencias del geómetra diferencial André Lichnerowicz (1915-1998). Tras algunas publicaciones, presentó su tesis Formules apparentées à celles de Gauss-Bonnet et de Nevanlinna-Ahlfors pour certaines applications d’une variété à n dimensions dans une autre en mayo de 1953, bajo la supervisión de Lichnerowicz.

Tras su doctorado, Marie-Hélène trabajó como asistente en varias universidades hasta que en 1964 fue nombrada profesora en la Universidad de Lille, donde permaneció hasta su jubilación en 1981. Durante esos años escribió numerosos textos y continuó con sus investigaciones. Jean-Paul Brasselet, alumno de Marie-Hélène resumía los logros de su directora de tesis con estas palabras:

Desde el estudio de las funciones de una variable compleja hasta las clases características de variedades singulares, el viaje matemático de Marie-Hélène Schwartz ha seguido un recorrido bien definido, superando todas las dificultades encontradas en el camino. […] Podemos distinguir en su recorrido matemático cuatro períodos cuyos temas abarcan sucesivamente las funciones de variable compleja, la teoría de Ahlfors, el teorema de Poincaré-Hopf para variedades singulares y campos radiales y, finalmente, las clases características de variedades singulares. Un punto común de estos trabajos es que eran de actualidad para la época, o, como veremos, muy adelantados a su tiempo.

A pesar de su delicada salud Marie-Hélène vivió casi hasta los cien años. Durante su larga vida le acompañaron sus incesantes dolores de cabeza, vivió tiempos muy duros durante la Segunda Guerra Mundial y sufrió la pérdida de su hijo Marc-André quien se suicidó en 1971.

Referencias

• Jean-Paul Brasselet, Marie-Hélène Schwartz et les champs radiaux, un parcours mathématique, Comptes Rendus. Mathématique 359 (3) (2021), 329-354.

• Yvette Kosmann-Schwarzbach, Women mathematicians in France in the mid-twentieth century, BSHM Bulletin: Journal of the British Society for the History of Mathematics 30 (3) (2015), 227-242.

• John J. O’Connor, Edmund F. Robertson, Marie-Hélène Schwartz, MacTutor History of Mathematics archive, University of St Andrews.

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad

El artículo Marie-Hélène Schwartz: el coraje de una matemática judía y trotskista se ha escrito en Cuaderno de Cultura Científica.

En la respuesta a una carta de una niña de doce años en 1943 Einstein escribió: “Querida Barbara: No te preocupes por tus dificultades con las matemáticas; te puedo asegurar que las mías son todavía mayores”. El que Einstein suspendiese matemáticas es solo un mito. Pero es cierto que no era un matemático particularmente creativo. Su fuerza estaba en la física, y veía las matemáticas meramente como un medio para un fin. En más de una ocasión tuvo que apoyarse en otros para que le ayudaran con algunos obstáculos matemáticos o basarse en trabajos, como los de Minkowski, que abrían nuevas perspectivas al propio.

Fotografía de Hermann Minkowski que ilustraba la publicación en 1909 de Jahresberichte der Deutschen Mathematiker- Vereinigung (Informes anuales de la asociación de matemáticos alemanes) donde se recogía su presentación del 21 de septiembre de 1908 en el 80º Congreso de Científicos Alemanes titulada Raum und Zeit (Espacio y tiempo).

Einstein se enseñó a sí mismo matemáticas y física a una edad bastante temprana. En 1949, en sus Notas autobiográficas, escribe que descubrió las maravillas de un libro “santo” de geometría (Elementos, de Euclides) a la edad de doce años. Atribuía al estudio tan temprano de las pruebas geométricas el haberle enseñado el disfrute de usar el pensamiento para resolver problemas. Basándose en libros fuera del programa de estudios Einstein siempre estuvo más adelantado que el resto de su clase. Sin embargo, las matemáticas no le emocionaban. Más adelante en su autobiografía escribe: “Mi interés en el conocimiento de la naturaleza era […] absolutamente más fuerte, y aún no estaba claro para mí como estudiante que el acceso a un conocimiento más profundo de los principios básicos de la física está unido a los métodos matemáticos más complejos”.

Esta parece una descripción bastante adecuada de la evolución de las matemáticas en las teorías de Einstein sobre la relatividad: al principio no le importó demasiado el aspecto matemático para descubrir más tarde lo importante que podía ser. Tras la publicación de la teoría especial de la relatividad en 1905, su profesor de matemáticas en el Politécnico de Zúrich Hermann Minkowski expresó su sorpresa, ya que no podía creer que ese joven que se había saltado tantas clases podía tener la capacidad de producir una teoría tan revolucionaria.

Y Minkowski aportó la elegancia

Después de un examen más detallado Minkowski descubrió que las matemáticas eran ciertamente menos elegantes de lo que él consideraba que debían ser. En esa época, había un grupo de élite de matemáticos alemanes y suizos que estaba convencido de que la física teórica era realmente demasiado difícil para los físicos y que, por lo tanto, debía ser dejada en manos de los que estaban mejor preparados para abordarla. Minkowski se dispuso a acudir al rescate. Sus resultados se presentaron en 1908.

Dado que la teoría especial de la relatividad implicaba cambiar el tiempo y el espacio, Minkowski creó una serie de herramientas para describir el espaciotiempo mismo. La primera reacción de Einstein fue negativa, porque pensaba que hacía su sencilla teoría infinitamente más complicada, pero rápidamente cambió de opinión. Las matemáticas de Minkowski le daban a la teoría especial de la relatividad tanto una base como un vocabulario, que abría la puerta para que otros pudiesen trabajar mejor con la nueva teoría. Y cuando Einstein puso su atención en el desarrollo de una extensión de su teoría de la relatividad para describir la gravitación, las matemáticas de Minkowski probaron ser muy útiles.

Einstein también recibió ayuda matemática para la teoría general de la relatividad. Publicó una versión de la teoría general de la relatividad en 1911 pero sabía que todavía quedaba trabajo por hacer. Recurrió a su amigo Marcel Grossmann, diciéndole que se volvería loco si no le ayudaba. Grossmann sugirió que una oscura rama de las matemáticas llamada geometría de Riemann podría ser aplicable, aunque, según la biografía de Einstein de Abraham Pais, Subtle is the Lord, Grossmann también le dijo a Einstein que era “un lío terrible en el que los físicos no deberían meterse”. A pesar de ello, Einstein se metió, y resultó que la geometría de Riemann era la pieza que faltaba para desarrollar sus ecuaciones de la teoría general de la relatividad, cuya versión final se publicaría en 1916.

Einstein, efectivamente, necesitó la ayuda de los matemáticos pero, como David Hilbert, un profesor de matemáticas de la Universidad de Gotinga, dijese:

“Cualquier niño de las calles de Gotinga comprende más de geometría de cuatro dimensiones que Einstein. Sin embargo, a pesar de ello, Einstein hizo el trabajo y no los matemáticos. ¿Sabes por qué Einstein dijo las cosas más originales y profundas acerca del espacio y el tiempo de nuestra generación? Porque no había aprendido nada sobre las matemáticas y la filosofía del espacio y el tiempo”.

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

Una versión anterior de este artículo se publicó en Experientia Docet el 6 de diciembre de 2009.

 

El artículo Einstein y las matemáticas de la relatividad se ha escrito en Cuaderno de Cultura Científica.

Lepisma. Insecto tisanuro nocturno, originario de América, de unos nueve milímetros de largo, con antenas prolongadas, cuerpo cilíndrico cubierto de escamas plateadas muy tenues, abdomen terminado por tres cerdillas articuladas, y pies cortos con dos artejos y una uña en cada tarso, que roe el cuero, el papel y el azúcar.

Diccionario de la Real Academia Española .

Trataremos de un invasor, según el DRAE, que, en realidad, no invade, pues parece que es de aquí, de nuestro entorno, y que, en todo caso, a quienes invade es a otros.

Lepisma saccharina. Fuente: Wikimedia Commons

Los pececillos de plata se conocen como lepismas, del griego escama, y que Linneo utilizó para dar el nombre al género que los define. La especie más común para referirse al pececillo de plata es Lepisma saccharina, aunque es un nombre común que a menudo se generaliza a otras especies parecidas. También es conocida como cordón de plata, lepisma de la harina, lepisma del azúcar, traza, comesantos, cucaracha de agua y sardineta chiripa.

Como las escamas que recubren su cuerpo brillan y reflejan la luz, su aspecto recuerda al brillo de metales como la plata. Y cuando se mueven, contornean el cuerpo y recuerdan a un pez y de ello su nombre popular de pececillo de plata.

Son insectos tisanuros, muy primitivos, con unas 400 especies, sin alas y sin crecimiento por metamorfosis y, por tanto, crecimiento continuo. Miden alrededor de un centímetro. Es posible que sus antecesores aparecieran hace 400 millones de años. Ahora, los taxónomos han dividido a los tisanuros y, con ellos a los pececillos de plata, y pertenecen al orden Zygantoma. En cada puesta ponen unos 60 huevos que necesitan de 19 a 43 días para eclosionar.

Viven en la hojarasca y bajo la corteza de árboles y se alimentan de restos vegetales. Abundan en las casas, sobre todo en las bibliotecas, y atacan y destruyen libros pues se alimentan de papel. También gustan de cuadros y tejidos. Necesitan una humedad alta en el entorno que habitan, entre el 75% y el 95%, y buscan la oscuridad pues son fototáxicos negativos, es decir, huyen de la luz.

Los lepismas más conocidos son las especies Lepisma saccharina y Thermobia domestica. La primera es el más conocido y, como escribe, José Luis Yela, del INIA de Madrid, se alimenta de celulosa y colas y adhesivos de papel. Es una especie cosmopolita, a pesar del no demostrado origen americano que indica el Diccionario y, antes Linneo. Puede ser numeroso en entornos umbríos, recogidos y húmedos. Recientemente, el grupo de Yiheng Zhou, de la Universidad Tongji de Shanghai, han secuenciado el ADN de esta especie.

La segunda especie, Thermobia domestica, es el insecto del fuego o termobia de las tahonas y, si bien sus preferencias, los daños que provoca y su biología se parece a lo descrito para el pececillo de plata, busca entornos temperatura alta y humedad. Su color también es plateado pero con un dibujo oscuro en el dorso. Para poner los huevos necesita de 32ºC a 41ºC. Se le encuentra cerca de los hornos de las panaderías, de calentadores de agua y de calderas de calefacción. Tienen distribución cosmopolita, en interior y exterior, y se debate su posible origen asiático. Se alimentan de carbohidratos y almidón, como harina y encuadernaciones de libros.

En resumen, se alimentan de carbohidratos, almidón y compuestos parecidos de libros, carpetas, ropa, café, caspa, pegamentos, pelo, pinturas, fotos, yeso, azúcar, papel pintado, tapicerías, algodón, cadáveres de insectos, lino, seda, migas de pan, cuero, … Puede vivir hasta un año sin comida mientras no falte agua. Y son presa de tijeretas y arañas.

Pueden digerir celulosa, el componente principal de las plantas, pues sintetizan la enzima celulasa que la degrada. Es una enzima que solo se conoce en otra especie animal, el molusco bivalvo Teredo navalis, que se alimenta y taladra madera. Los animales herbívoros, para digerir la celulosa de los vegetales que son su alimento, tienen microorganismos simbiontes que lo hacen en su tubo digestivo.

Hay estudios para eliminar la presencia de pececillos de plata en las casas, a menudo con poco éxito por su habilidad para escapar y esconderse. Una de las investigaciones quizá con futuro es el ensayo con aceites de las hojas del cedro japonés Cryptomeria japonica publicado por Sheg-Yang Wang y sus colegas de la Universidad Nacional de Taiwan en Taipei. Una concentración de estos aceites no muy alta en papel repele al 80% de los lepismas. Y los vapores durante 10 horas alcanzan una tasa de mortalidad del 100%. Todavía sin confirmar parece que los vapores de eucalipto consiguen un efecto parecido.

El origen del pececillo de plata, que nuestro Diccionario sitúa en América, veremos que es tema de debate. Es posible que la propuesta llegó al Diccionario desde el Systema Naturae de Linneo, en la edición de 1758, que afirma que vive en América pero, añade, que es habitual en Europa. Para Rafael Molero Baltanás y sus colegas, de la Universidad de Córdoba, Lepisma saccharina no tiene su origen en América, y los muestreos en la región mediterránea y, en concreto, en la Península Ibérica y Marruecos, indican que aparece en entornos exteriores y naturales. Las citas anteriores al estudio de Molero Baltanás encuentran el pececillo de plata en la Península, además de Baleares y Canarias. Y las nuevas citas que publican en 2014 demuestran su presencia tanto en entornos doméstico como en hábitats naturales y en casi todas las regiones de la Península.

En Europa central y del norte y en América es una especie vinculada a la especie humana por dónde vive y, quizá, fue introducida en viajes y exploraciones. Es curioso y poco conocido que el pececillo de plata y otras especies cercanas del orden Zygentoma también se han encontrado habitando en hormigueros. Incluso imitan el sistema de reconocimiento entre hormigas por la secreción de compuestos orgánicos en la cutícula. En un estudio reciente, Ruben Claus y sus colegas, de la Universidad de Gante, en Bélgica, en el que participa Rafael Molero Baltanás, recuerda que el pececillo de plata, Lepisma saccharina, no es habitual que se asocie con hormigas en Europa. Sin embargo se ha encontrado en hormigueros de la hormiga Formica rufa en España, Portugal, Alemania y Bélgica.

En resumen, en nuestro entorno más cercano no es una especie invasora y es posible que lo sea en otros lugares. Su distribución y conducta recuerda a las cucarachas y su distribución actual. Hay que actualizar la descripción que aparece en el Diccionario.

Y, para terminar, un texto escrito para una periódico de gran tirada, El País, por un autor conocido, Juan José Millás, y que trata del pececillo de plata, y que reproducen Rafael Molero Baltanás y sus colegas, en 2014, en el Boletín de la Sociedad Entomológica Aragonesa. Se titula Oración y apareció en la contraportada del diario:

Hay un insecto microscópico, el lepisma, también llamado por su aspecto pececillo de plata, que vive en los libros igual que un delfín en las profundidades del océano, surcando las páginas como si fueran láminas de agua sucesivas. Puede alojarse indistintamente en un volumen de Kafka o Flaubert, de Melville o Poe, sin que el grado de salinidad de escrituras tan diferentes afecte a su organismo. El lepisma navega, pues, en el interior de la masa de papel recorriendo títulos, textos y texturas, aunque lo normal es que si nace en Moby Dick muera en esta novela sin cruzarse jamás, curiosamente, con la ballena blanca, su pariente lejano.

El lepisma ignora también la existencia del lector, tampoco nosotros nos damos cuenta de que junto al argumento imaginario que forman las palabras, en cada hoja está sucediendo un drama real protagonizado por una familia de pececillos de plata que se alimentan de las comas de nuestros textos preferidos. Nos acompañan en la travesía lectora como los delfines a los navegantes, saltando fuera de la página y zambulléndose en ella a través de un adverbio, que atraviesan sin romperlo ni machacarlo.

Cuánta gente vive de la literatura, pues. Es increíble. Estos lectores sin alfabetizar que se alimentan paradójicamente de nuestras publicaciones son los más ingenuos sin duda, pero conviene tenerlos en cuenta. Quizá el universo no sea más que un gigantesco libro que alguien lee con pasión mientras nosotros, sus lepismas, navegamos por él pese a ignorar su sintaxis. A ese lector gigante le dedico este artículo con el ruego de que, cuando se canse de leer, cierre el libro sin violencia, para no hacernos daño.

Referencias:

Claus, R. et al. 2022. Established populations of the indoor silverfish Lepisma saccharinum (Insecta: Zygentoma) in red wood and nests. Belgian Journal of Zoology 152: 45-53.

Guerrero C. & F. Rueda. 1988. Los insectos y el hombre. Penthalon Ed. Madrid. 169 pp.

Joshi, M.J. et al. 2020. Silverfish (Lepisma saccharina): An overview and their management. Agriculture & Foods: e-Newsletter 2: March 23155.

Molero Baltanás, R. et al. 2014. Lepismas y libros: Actualización del conocimiento sobre Lepisma saccharina (Zygentoma: Lepismatidae) en España. Boletín SEA 54: 351-357.

Wang, S.-Y. et al. 2006. Essential oil from the leaves of Cryptomeria japonica acts as a silverfish (Lepisma saccharina) repellent and insecticide. Journal of Wood Science 52: 522-526.

Wikipedia. 2021. Thermobia domestica. 3 mayo.

Wikipedia. 2022. Lepisma saccharina. 29 enero.

Wikipedia. 2022. Silverfish. 30 May.

Yela, J.L. 1997. Insectos causantes de daños al patrimonio histórico y cultural: caracterización, tipos de daño y métodos de lucha (Arthropoda: Insecta). Boletín SEA 20: 111-122.

Zhou, Y. et al. 2022. Profiles of telomeric repeats in Insecta reveal diverse forms of telomeric motifs in Hymenopterans. Life Science Alliance doi: 26508/lsa.202101163.

Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.

Para saber más:

Los invasores: Invasiones biológicas
Especies exóticas invasoras

El artículo Los invasores: Pececillos de plata se ha escrito en Cuaderno de Cultura Científica.

Un nuevo estudio realizado en Atapuerca ha llegado a la conclusión de que los homínidos que vivieron allí hace entre 1,2 y 0,4 millones de años llegaban a la madurez antes que los seres humanos modernos. A esta conclusión se llega tras analizar y comparar las coronas de sus dientes.

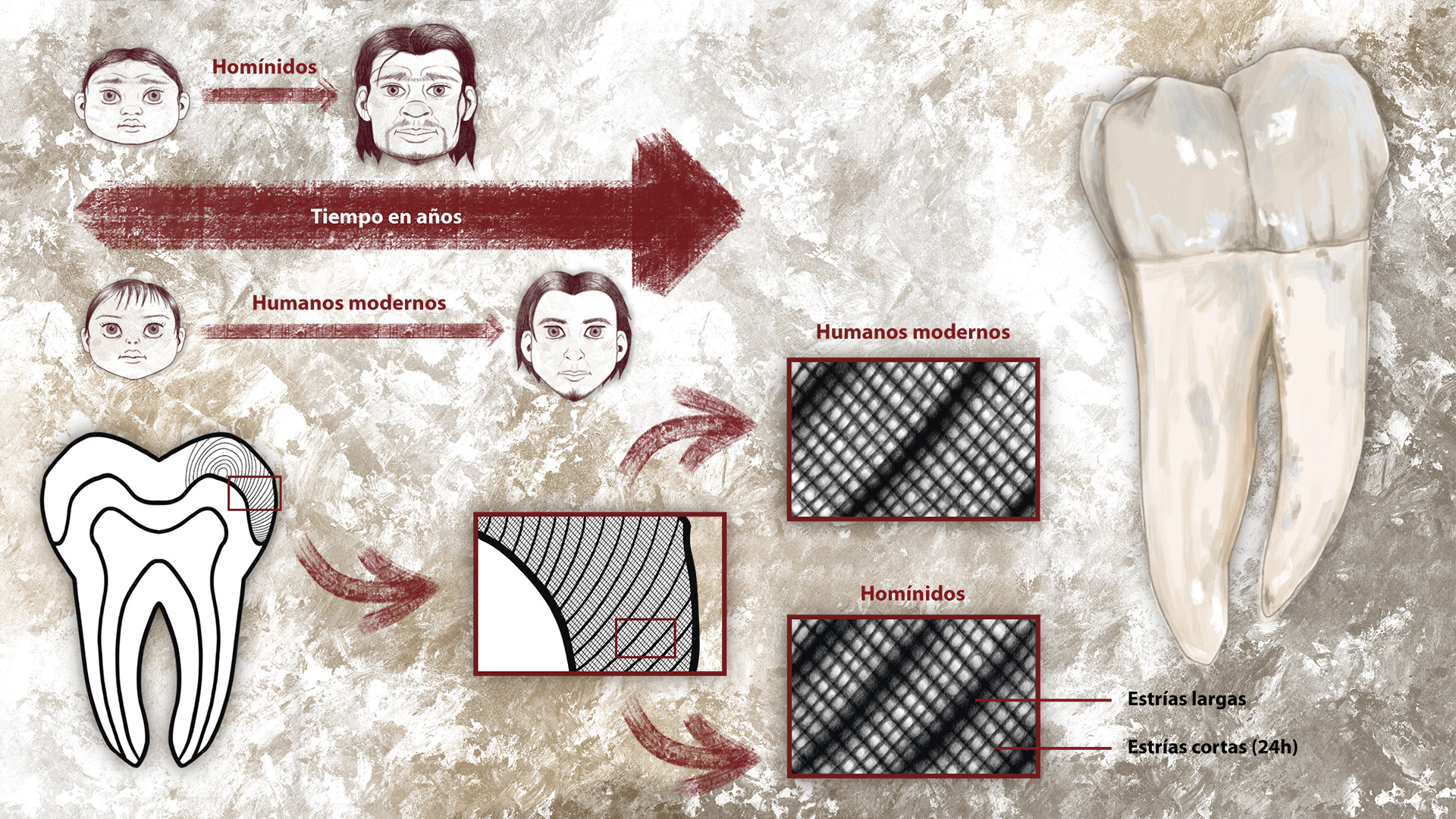Diferencias en la maduración de los homínidos. Comparación de la maduración de los homínidos de Atapuerca y de los humanos actuales tomando como referencia las estrías largas y cortas de las coronas de sus dientes. Ilustración: Nerea Goikoetxea Zabala.

La corona de los dientes crece de manera circular, formando anillos concéntricos a intervalos regulares, al igual que los troncos de los árboles, las cebollas o el pelo. Este crecimiento crea líneas que aparecen en la superficie del esmalte de los dientes. Podemos diferenciar dos tipos de estrías: largas y cortas.

Estas últimas (también llamadas estrías transversales) tienen un crecimiento circadiano, es decir, se generan cada veinticuatro horas. Los ameloblastos, aquellas células encargadas de la formación del esmalte, detienen su actividad durante un corto período de tiempo de manera periódica, dando lugar a las estrías largas, estrías de Retzius o perikymata (plural de perikyma). El número de estrías cortas entre dos estrías largas sucesivas varía entre seis y once, es constante para el mismo individuo y diferente en cada especie de homínidos. Gracias al conteo de estas líneas, puede conocerse con gran precisión el tiempo de desarrollo del esmalte de los dientes.

Para este estudio, un equipo de científicos del Centro Nacional de Investigación sobre la Evolución Humana (CENIEH) analizó una amplia muestra de dientes de diferentes homínidos del Pleistoceno Inferior y Pleistoceno Medio de Europa, concretamente de la sierra de Atapuerca.

El desarrollo dentario de estos homínidos se estudió desde dos puntos de vista complementarios. El primero trata de la evaluación del momento absoluto de la formación de la corona utilizando las marcas de crecimiento presentes en la microestructura del esmalte. El segundo evalúa el tiempo relativo de formación de todos los dientes en un espécimen específico en comparación con los humanos modernos.

Para ello se utilizaron diferentes herramientas: el número de perikymata, la distribución de perikymata (medido como el número de perikymata por decil de altura) y la periodicidad de perikymata (que es la cantidad de estrías cortas entre dos estrías largas).

Por un lado, se examinaron el número y la distribución de perikymata de 286 piezas dentales: 96 del yacimiento de la Sima de los Huesos (430 000 años), 22 de Homo antecessor y 68 dientes no desgastados de una muestra de diferentes poblaciones de Homo sapiens. Por otro, se calculó la periodicidad de perikymata de 14 dientes (fracturados de manera natural) de homínidos de los tres yacimientos: el nivel TE9 de la Sima del Elefante (1,2 millones de años), el nivel TD6.2 de Gran Dolina (850 000 años) y la Sima de los Huesos.

Una novedad de esta investigación, a diferencia de los estudios anteriores, es que se han analizado dientes molares y premolares cuando antes solo se habían utilizado incisivos y caninos. Además, los métodos usados para reconstruir los dientes desgastados son ahora mucho más precisos. Estos estudios previos carecen de observaciones directas sobre el incremento del crecimiento en el esmalte de período corto (estrías transversales) en individuos, así como de los números observados entre estrías adyacentes de período largo de Retzius, la denominada periodicidad.

El principal problema al que se enfrentaron los científicos es el desgaste dental, efecto de la masticación. Las alturas de sus coronas originales se estimaron empleando un nuevo método de reconstrucción, una técnica estadística basada en regresiones polinomiales que permite estimar el porcentaje de esmalte perdido.

Los resultados indican que el crecimiento del esmalte de los homínidos de Atapuerca podría ser hasta un 25 % más rápido que en el Homo sapiens. Lo que significa que estos homínidos llegaban a la edad adulta varios años antes que nosotros.

Referencias consultadas:

Modesto-Mata, M., Dean, M.C., Lacruz, R.S. et al. (2020, marzo 13). Short and long period growth markers of enamel formation distinguish European Pleistocene hominins. Scientific Reports, 10. doi: 10.1038/s41598-020-61659-y

SINC. (2020, marzo 13). El esmalte de los homínidos de Atapuerca crecía más rápido que el de los humanos modernos. Agencia SINC.

Smith, T.M. et al. (2010, diciembre 7). Dental evidence for ontogenetic differences between modern humans and Neanderthals. Proceedings of the National Academy of Sciences. doi: 10.1073/pnas.1010906107

Ramírez, F.V., (1996). Líneas de crecimiento en el esmalte dentario. Aplicación a los homínidos del Plio-Pleistoceno. Revista Argentina de Antropología Biológica, 1 (1), 182-197.

 

Autora: Nerea Goikoetxea Zabala (@goikoilustra). Graduada en arte. Especialista en Ilustración Científica, UPV/EHU. Curso 20/21.

“Ilustrando ciencia” es uno de los proyectos integrados dentro de la asignatura Comunicación Científica del Postgrado de Ilustración Científica de la Universidad del País Vasco. Tomando como referencia un artículo de divulgación, los ilustradores confeccionan una nueva versión centrada en la propia ilustración

El artículo Los homínidos de Atapuerca maduraban antes que nosotros se ha escrito en Cuaderno de Cultura Científica.

¿Estamos realmente diseñados para conectar con los demás? Si es así, ¿por qué siguen existiendo los psicópatas? ¿Se pueden tratar trastornos delirantes como la paranoia desde el punto de vista de la evolución? O ¿cómo ha cambiado la atracción sexual desde la época de nuestros ‘abuelos’ homínidos hasta ahora?

A estas y otras cuestiones relativas a la evolución del comportamiento humano se trató de dar respuesta durante la IV Jornada Nacional de Evolución y Neurociencias, evento organizado por la Cátedra de Cultura Científica de la UPV/EHU y la Red de Salud Mental de Bizkaia, que tuvo lugar los días 28 y 29 de abril en el Bizkaia Aretoa – UPV/EHU de Bilbao.

Desde que en 2017 un grupo de psiquiatras de la Red de Salud Mental de Bizkaia organizara la primera edición de esta jornada, la cita se ha convertido en un punto de encuentro para profesionales de distintos ámbitos científicos como la psiquiatría, la psicología, la biología o la filosofía con un interés común: la conducta humana desde una perspectiva evolucionista y su divulgación científica en un formato accesible y ameno para todos los públicos, a la par que riguroso y actualizado.

La enfermedad mental, como el resto de enfermedades, tiene un sustrato biológico. Las paranoias, las ideas delirantes, tienen estabilidad en el tiempo porque, a pesar de su aparente heterogeneidad, responden a alteraciones en determinadas estructuras cerebrales. La posibilidad de estas alteraciones es consecuencia directa de la evolución. Luis Caballero, jefe de la Sección de Psiquiatría en el Hospital Universitario Puerta de Hierro y profesor asociado del Departamento de Psiquiatría de la Universidad Autónoma de Madrid, expone el caso.



Para saber más:

El gran encéfalo humano es un “encéfalo social”
Nuestro cerebro no piensa (y el de usted, tampoco)

Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus

El artículo IV Jornada Nacional de Evolución y Neurociencias: Luis Caballero – Trastornos delirantes desde una perspectiva evolucionista se ha escrito en Cuaderno de Cultura Científica.

Jorge Hernández Bernal y Santiago Pérez Hoyos

Salida de la Tierra, fotografía tomada por William Anders ​durante la misión del Apolo 8 a la Luna el 24 de diciembre de 1968. Fuente: NASA

 

Hace no tanto tiempo las noches eran oscuras y llenas de estrellas. La Luna parecía inalcanzable y los astros eran nuestro modo de orientarnos. Impulsado por el uso que hacemos de la ciencia y la tecnología, hoy el mundo ha cambiado. Las noches ya no son oscuras y las estrellas palidecen, hemos alcanzado la Luna y contamos con avanzados sistemas de geolocalización por satélite.

El espacio está cada vez más presente en nuestras vidas. En los últimos años el sector ha crecido rápidamente con la llegada de nuevas potencias y empresas privadas. Gran parte de este desarrollo se ha producido sin el escrutinio del conjunto de la sociedad civil. Y sin una reflexión que nos permita elegir conscientemente la forma de relacionarnos con estas nuevas realidades. Por ello es necesaria una ética espacial, una ética aplicada al espacio y análoga de la bioética. A través de ella podemos intentar responder cuestiones que van tomando forma. En algunos casos, hipotéticas; en otros, acuciantes.

Problemas que piden una ética espacial

Algunos de los problemas que aborda la ética espacial son bastante conocidos. Es el caso de la basura espacial. ¿Cómo deberíamos regular las actividades espaciales en la órbita terrestre? ¿Deberían seguir lanzándose megaconstelaciones de satélites?

Otras problemáticas son menos conocidas, pero ya están presentes: los lanzamientos espaciales suponen una creciente huella ecológica. ¿Es igual de aceptable contaminar para practicar turismo espacial que para lanzar un satélite meteorológico?

Multitud de iniciativas actuales buscan enviar humanos a la Luna y a Marte. ¿Sería correcto habitar estos astros permanentemente, o las actividades deberían limitarse a expediciones científicas temporales? ¿Qué grado de impacto ambiental es tolerable? ¿Se pueden extraer recursos naturales de estos astros? E, incluso, ¿se pueden comercializar esos recursos?

La minería espacial es una de las grandes problemáticas a medio plazo. Los asteroides del sistema solar contienen multitud de recursos con valor económico. Varias empresas están ya trabajando en ello, y algunos países se han apresurado a introducir legislaciones que respalden este tipo de actividades, cuyo encaje en los tratados internacionales vigentes es confuso.

¿Deben estos recursos ser de quien primero los alcance o debe haber algún tipo de reparto global? ¿Qué efectos puede tener sobre la economía y los equilibrios geopolíticos la introducción de nuevos recursos actualmente escasos? Si usamos estos recursos para continuar con el crecimiento extractivista, ¿no acabaríamos chocando con los límites del sistema solar como chocamos actualmente con los de la Tierra?

Ya existen proyectos para extraer y comercializar agua en el espacio. El agua, previamente separada en hidrógeno y oxígeno, podría ser un combustible muy conveniente para futuras naves espaciales. En la Tierra el agua es un recurso renovable, pero en el espacio, al ser expelida por los motores de las naves espaciales, se perdería para siempre. Por lo que a largo plazo se convertiría en un recurso estratégico y no renovable, además de esencial para la vida. ¿Cómo garantizar el derecho al agua en estas condiciones?

Si algún día establecemos colonias humanas en el espacio, ¿cómo garantizamos el bienestar de los colonos? ¿Cómo evitar situaciones cercanas a la esclavitud como las que se dan actualmente en alta mar? ¿Habrá que actualizar los Derechos Humanos para adaptarlos a las condiciones específicas del espacio?

Otra consecuencia de las actividades espaciales puede ser la alteración de los entornos espaciales. ¿Qué grado de alteración es tolerable? ¿Sería aceptable terraformar Marte? ¿Qué tratamiento deberíamos darle a la vida extraterrestre? ¿Deberíamos proteger la cara visible de la Luna para que las futuras generaciones sigan viendo la misma Luna que ha fascinado a tantas culturas durante milenios?

La cara visible de la Luna tiene un gran valor cultural para los habitantes de la Tierra. ¿Cambiaremos su aspecto a través de la minería o la edificación? ¿Deberíamos conservar este patrimonio cultural para las futuras generaciones o renunciar a él?Una reflexión necesaria en español

El futuro del sector espacial, como el de la humanidad en su conjunto, depende de la gestión que hagamos en los próximos años de la crisis climática y ecológica. La reflexión de la ética espacial es necesaria para que la exploración del espacio sea una aventura sensata y acorde al interés general. Los problemas del espacio deben estar al alcance de la opinión pública.

Hace tiempo que existe una reflexión sobre este tema en lengua inglesa. Ahora un grupo de académicos y profesionales nos hemos propuesto traer esta reflexión a la lengua española. Con este fin, los días 11 y 12 de julio de 2022 organizaremos en Bilbao un curso de verano de la Universidad del País Vasco. Este curso constituye la primera aproximación en lengua española a la ética espacial, y está abierto a la participación, presencial u online, de todo tipo de público.

Sobre los autores: Jorge Hernández Bernal y Santiago Pérez Hoyos son investigadores en el Grupo de Ciencias Planetarias, Universidad del País Vasco / Euskal Herriko Unibertsitatea

Este artículo fue publicado originalmente en The Conversation. Artículo original.

Para saber más:

Rusia contra Estados Unidos: por qué la exploración espacial debe contar con todos
¿Cuál es la huella ecológica del turismo espacial?

El artículo Por qué necesitamos una ética espacial se ha escrito en Cuaderno de Cultura Científica.

Pasaron otros treinta años desde que a Günther Christoph Schelhammer se le ocurrió a utilizar un tenedor para diagnosticar la sordera de sus pacientes, hasta que el diapasón adquirió su forma actual. Cuando lo hizo, no fue en manos de los otorrinos, sino gracias a un trompetista inglés.

A principios del siglo XVIII, Londres se había convertido en uno de los principales centros musicales del Barroco. Allí compusieron algunas de sus obras más conocidas compositores de la talla de Henry Purcell1 o Georg Friedrich Händel. Curiosamente, ambos le dedicaron varias partituras a una familia de músicos de apellido Shore: Matthias Shore, su hermano William y su hijo John eran trompetistas en la Capilla Real de Londres. Su hija, Katherine Shore fue cantante, actriz y tocaba también el clave. Todos fueron músicos destacados, pero además John Shore saltó a la fama por su virtuosismo como solista, o bien tocando a dúo junto a su hermana Katherine y otros cantantes de la época. Tenía un control y una agilidad con la trompeta que se consideraban únicos.

Todo cambió por culpa de un concierto. John debió de hacer un sobreesfuerzo tocando la trompeta y su labio, de repente, se desgarró. La herida resultó ser irreparable y Shore tuvo que abandonar su carrera como solista. Por suerte, además de un gran virtuoso, era también un tipo versátil. Había recibido una gran formación musical desde joven. Sabía tocar el laúd, reparar instrumentos, y le gustaba innovar y aprender técnicas nuevas. Después del accidente, se volcó en su faceta de laudista, y fue para afinar su instrumento que, en 1711 dio con la idea del diapasón. Se cuenta que desde entonces, antes de cada concierto y de forma muy teatral, sacaba esta curiosa horquilla metálica ante el público y repetía: “Nunca voy a ningún lado sin mi diapasón”2. ¡Eso sí que debió de ser una campaña de promoción!

El diapasón pronto se popularizó por toda Europa —aunque no necesariamente gracias al eslogan de Shore. Hasta entonces, los músicos habían recurrido a tubos de madera en busca de una referencia tonal. Pero estos eran poco fiables y se veían muy afectados por los cambios de temperatura y humedad del ambiente. El diapasón, por el contrario, era manejable y robusto, mantenía su tono constante independientemente de las condiciones ambientales y, además, produce un tono muy puro, sin apenas armónicos, que resulta muy fácil de identificar.

El diapasón de Händel

El mismo Händel acogió enseguida el invento. Debió de regalárselo el mismísimo John Shore, y a día de hoy, su diapasón es el más antiguo que se conserva. Sin embargo, si alguien lo hiciera sonar, notaría una diferencia muy importante respecto a uno actual. Para empezar, porque no dan la misma nota: los diapasones actuales suelen dar un la (A4003), mientras que el de Händel sonaba como un do (C512 Hz). Pero además, resulta que ese do nos sonaría bastante desafinado, casi un cuarto de tono más grave que el actual (C523 Hz)4.

La existencia de este diapasón permite a los musicólogos identificar la afinación exacta a la que Händel y sus contemporáneos deseaban escuchar sus obras (el tono de los diapasones ha permanecido estable hasta hoy). Pero además, nos da pistas sobre los cambios que han experimentado los sonidos musicales a lo largo de los últimos siglos5. En 1880, el erudito musical inglés A. J. Ellis6 hizo un viaje por toda Europa y examinó 74 órganos y diapasones de entre los siglos XVI y XIX, incluidos el diapasón de Händel y el del fabricante de pianos Stein, que construyó los pianos para Mozart en Viena. Descubrió que la frecuencia de afinación del la entre estos 74 instrumentos variaba en un rango de 374 a 567 vibraciones por segundo: el equivalente a un intervalo de quinta, o lo que en términos musicales viene a ser mogollón.

Este es el drama, la paradoja de toda esta historia: si bien el diapasón podía ayudar a producir un tono estable, constante a lo largo del tiempo, decidir qué frecuencia debía tener ese tono iba a ser mucho más complicado. Por eso, aunque los diapasones pronto estuvieron presentes en todos los centros musicales de Europa, no compartieron un estándar común hasta mucho tiempo después. A este invento le sucedió algo parecido que a los relojes: una cosa es aprender a medir el tiempo de forma precisa y estable, y otra muy distinta, ponerse de acuerdo en qué hora es. Resulta que el segundo problema es mucho más complicado, porque requiere poner de acuerdo a un montón de humanos. En el caso del reloj, el ferrocarril fue la clave para transportar la hora de un punto a otro del mapa y unificarla —la gente tenía que saber en qué momento llegar a la estación y para eso era necesario que distintas ciudades y países se pusiesen de acuerdo en un estándar. En el caso del diapasón, el encargado de hacer viajar ese buscado la universal, fue la radio.

El la universal de la BBC Foto: Alessandro Cerino / Unsplash

Antes de ese momento, hubo varios intentos de estandarización, pero ninguno llegó a triunfar del todo. Durante el siglo XIX, la música se fue haciendo más aguda, un semitono aproximadamente. Esta tendencia al alza respondía a una competición entre los propios músicos por conseguir un sonido “más brillante”, pero ocasionaba problemas a los cantantes, que no podían tensar sus cuerdas vocales indefinidamente. En 1859, el gobierno francés intentó ponerle freno y decretó que en adelante se aplicaría un la de 435 Hz en todo el país. Fue el primer intento de establecer un la común para todos, y aunque no logró imponerse por completo fuera de las fronteras francesas (de hecho, pasó a ser conocido como “tono francés”), sí frenó la escalada rampante de los sonidos musicales. A finales de siglo, los ingleses definieron su propio la en 439 Hz (supongo que por llevarle la contraria a los franceses, mayormente).

La aparición de la radio y su uso para difundir conciertos en Europa y Estados Unidos, hicieron más necesario que nunca fijar un estándar realmente internacional. En mayo de 1939, una conferencia en Londres acordó el estándar actual de A440. Se eligió esta nueva cifra en busca de una mayor precisión, ya que 439 es un número primo y resultaba más difícil de generar electrónicamente. El estándar A440 fue aprobado por el Instituto Británico de Estándares en 1939 y por la Organización Internacional de Estándares en 1955 y 1975. A partir de ese momento, la BBC comenzó a transmitir una señal de 440 Hz como tono de sintonización, el primer la realmente universal.

Y por fin todo fue unión y armonía en el mundo de las ondas… ¿o no? De hecho, y a pesar del estándar vigente, hoy en día la mayoría de las orquestas europeas afinan a A442. ¡Si es que no tenemos remedio!

Notas y referencias:

1Si no conoces nada suyo, te recomiendo echarle una oreja a esto.

2Bickerton, R. C., and G. S. Barr. “The origin of the tuning fork.” Journal of the Royal Society of Medicine, vol. 50, 1987, pp. 771-773.

3La afinación se suele designar con una letra, que sirve para nombrar las notas de la escala musical en el sistema anglosajón, seguida por su frecuencia en hercios. En este caso, A es la, por lo que A440 significa que el la se afina a 440 Hz. C512 indica la frecuencia del do.

4Si usásemos el diapasón de Händel para afinar, el la sonaría a 430 Hz.

5Feldmann, H. (1997). History of the tuning fork. I: Invention of the tuning fork, its course in music and natural sciences. Pictures from the history of otorhinolaryngology, presented by instruments from the collection of the Ingolstadt German Medical History Museum. Laryngorhinootologie, 76(2), 116–122. DOI: 10.1055/s-2007-997398

6Elis, A. J. The History of Musical Pitch. Nature 21(1880)50-54

Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica

El artículo En busca del la universal se ha escrito en Cuaderno de Cultura Científica.

En la anterior entrada del Cuaderno de Cultura Científica, titulada Universo pandigital, estuvimos hablando de números pandigitales, tanto de sus curiosas propiedades, como de algunos números pandigitales sorprendentes, así como de expresiones aritméticas pandigitales que se han utilizado para crear rompecabezas matemáticos, como las sumas o productos pandigitales. En esta entrada vamos a seguir en esta línea con las denominadas fracciones pandigitales, de las que ya hablamos de pasada en la entrada Fracciones sorprendentes.

El primer problema de ingenio publicado que esté relacionado con las fracciones pandigitales está recogido, según el matemático estadounidense David Singmaster, en el libro Mathematische Kurzweil (Diversión matemática) del alemán Louis Mittenzwey, publicado en Leipzig en 1880.

Problema 141 (Louis Mittenzwey): Utilizar las cifras 1, 2, …, 9 para formar tres fracciones cuya suma sea uno (1).

Las soluciones que aparecen en el texto son:

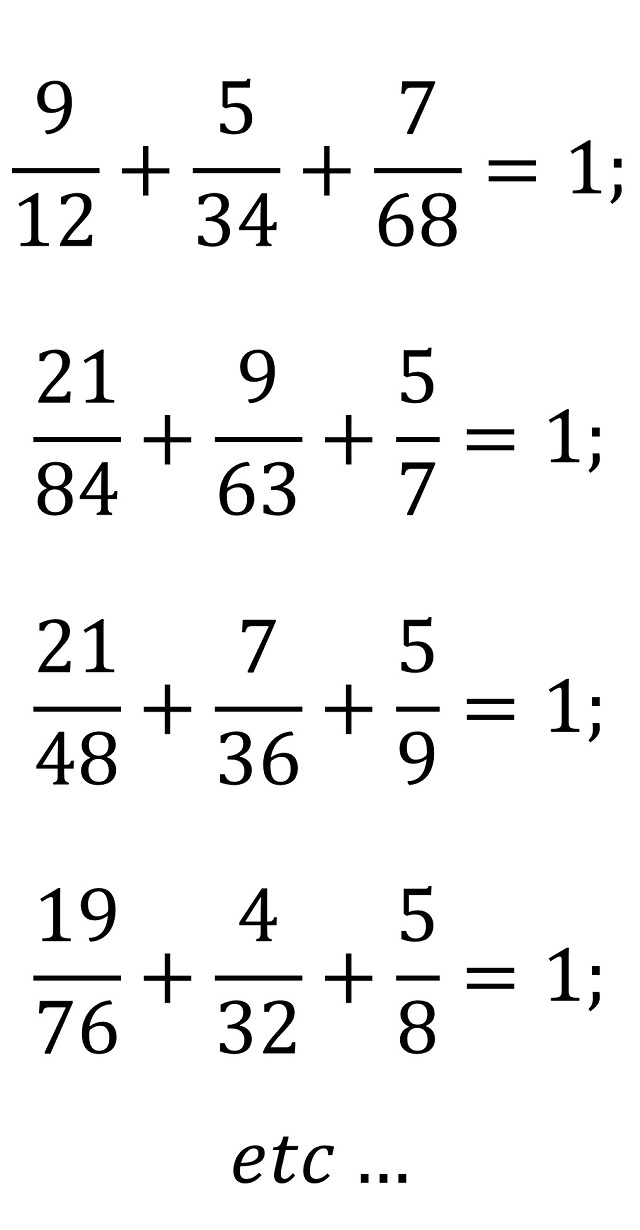
El inventor, coleccionista y comunicador de rompecabezas matemáticos y juegos de ingenio japonés Nob Yoshigahara (1936-2004), quien recibió el Premio Sam Loyd en 2003, recuperó este problema, pero solo para fracciones de la forma a/bc, de manera que es problema se podría plantear de la siguiente forma.

Problema (Nob Yoshigahara): Colocar las cifras 1, 2, 3, …, 9 en las casillas para que la siguiente suma de fracciones tenga sentido.

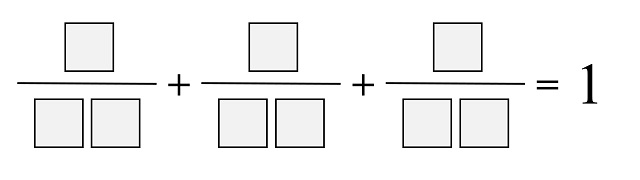
La única solución es la de este tipo que aparece como solución al problema 141, de Louis Mittenzwey.

Con motivo de mi entrada Universo pandigital, alguien me comentaba en Facebook que el matemático colombiano Bernardo Recamán Santos (imagino que en su libro Las nueve cifras y el cambiante cero, publicado por la editorial Gedisa) incluía una versión más extendida de este, ya que permitía que la suma fuese no solo 1, sino cualquier número natural N.

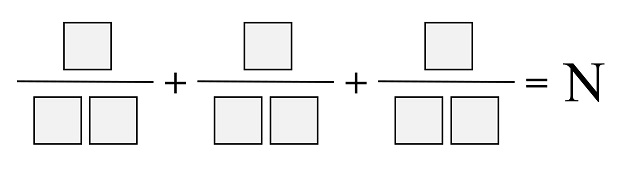
Para las personas que estáis leyendo esto queda este problema, para los casos en los que N no es 1. ¡A divertirse!

La siguiente aparición de fracciones pandigitales en libros de rompecabezas matemáticos fue en el texto Libro de puzzles estándar del siglo XX (1907), de Arthur Cyril Pearson. Curiosamente no aparecen como un problema abierto, sino como una anécdota numérica, titulada Malabares con las cifras.

Malabares con las cifras: Las nueve cifras básicas 1, 2, 3, …, 9 pueden ser colocadas de forma que se obtengan fracciones equivalentes a una de las siguientes 1/2, 1/3, 1/4, 1/5, 1/6, 1/7, 1/8 y 1/9, como

Por supuesto, que hay más formas de conseguirlo. De hecho, David Wells en su libro The Penguin Dictionary of Curious and Interesting Numbers comenta que existen existen 12 formas curiosas de utilizar las 9 cifras básicas, 1, 2, 3, 4, 5, 6, 7, 8, 9, para escribir la fracción 1/2. Las formas, más pequeña y mayor, son: 6729/13458 y 9327/18654.

Como no podía ser de otra forma, volvemos a encontrarnos al inventor de rompecabezas matemáticos y juegos de ingenio británico Henry E. Dudeney (1857-1930). En su celebrado libro Amusements in Mathematics / Diversiones matemáticas (1917) aparecen varios problemas, como el problema 88, llamado división digital.

División digital (Henry E. Dudeney): Otro buen rompecabezas consiste en ordenar las nueve cifras (excluyendo el cero) en dos grupos, de modo que uno de ellos, al ser dividido por el otro, produzca un número determinado sin resto. Por ejemplo, 13.458 dividido por 6.729 da 2. ¿Puede el lector encontrar distribuciones similares que produzcan 3, 4, 5, 6, 7, 8 y 9 respectivamente? Además, ¿puede encontrar los pares de números más pequeños posibles en cada caso? Así, 14.658 dividido por 7.329 es tan correcto para 2 como el anterior ejemplo que hemos dado, pero los números son mayores.

Antes de adentrarnos en la solución a este problema (que obviamente está ligado al anterior), comentar que existen algunas curiosidades más relacionadas con este problema. Por ejemplo, si tomamos la fracción 14.865/2.973, que es igual a 5, resulta que reordenando los dígitos de numerador y denominador obtenemos de nuevo una fracción pandigital cuyo valor es también 5, en concreto, 18.645/3.729. Aunque ninguna de ellas es la buscada, la fracción de números más pequeños posibles. Esta es 13.485/2.697, que también podemos reordenar para obtener una cuarta fracción pandigital de valor 5, 13.845/2.769.

La solución al rompecabezas de la división digital es la siguiente:

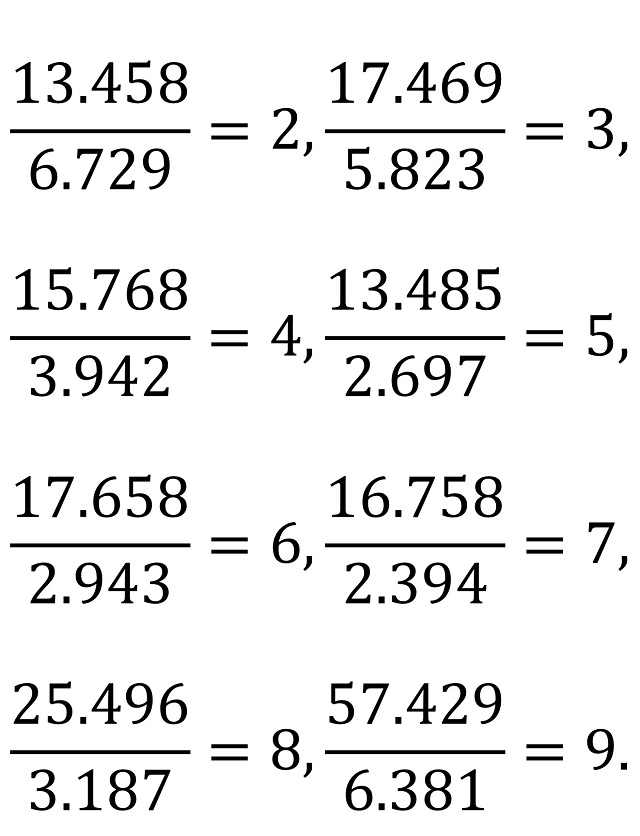
A este problema le seguían otros en el libro, como el problema 90, llamado el rompecabezas del siglo.

El rompecabezas del siglo: ¿Puede el lector escribir 100 en forma de un número mixto, utilizando cada una de las nueve cifras, una vez y sólo una vez? El distinguido matemático francés Edouard Lucas, ya fallecido, encontró siete formas diferentes de hacerlo, y expresó sus dudas sobre la existencia de otras formas. De hecho, sólo hay once formas y ninguna más. Aquí está una de ellas, 91 5.742/638. Nueve de las otras formas tienen igualmente dos cifras en la parte integral del número, pero la undécima expresión sólo tiene una cifra. ¿Puede el lector encontrar esta última forma?

Antes de continuar, recordemos a qué se refiere el autor con un número mixto y por qué el número 91 5.742/638 lo es. Para empezar, en la entrada Números errores de impresión), estuvimos hablando de lo que se conoce como fracciones mixtas. Una fracción mixta es una fracción impropia, es decir, el numerador es mayor que el denominador (ambos positivos), luego su valor es mayor que 1, que se representa como un número entero y una fracción propia. Por ejemplo, 3/2 es una fracción impropia, que se representa como 3/2 = 1 1/2, queriendo indicar que es la suma de 1 y 1/2 (esto es, 3/2 = 1 + 1/2, pero en la representación de la fracción mixta se omite el +). Cuando Dudeney habla de un número mixto sería una expresión de ese tipo, pero tal que la parte de la fracción no es una fracción propia, sino que su valor es un número natural. Así, el número mixto que aparece en el enunciado del rompecabezas es 91 5.742/638, cuyo valor es 91 + 5.742/638 = 91 + 9 = 100.

La solución a este problema la podéis intentar buscar vosotros mismos, ya que es la diversión que esconden los rompecabezas matemáticos. En cualquier caso, para quienes quieran consultarla o comprobar si la han obtenido, aquí la tenéis.

Pero Dudeney plantea, en el problema 91 (llamado Más números mixtos), también obtener números mixtos pandigitales cuyo valor sea cualquier número menor que 100.

Más números mixtos: Cuando publiqué por primera vez mi solución al último acertijo, me vi obligado a intentar la expresión de todos los números sucesivos hasta el 100 mediante una fracción mixta que contuviera las nueve cifras. Aquí hay doce números para que el lector pruebe su mano: 13, 14, 15, 16, 18, 20, 27, 36, 40, 69, 72, 94. Utilice cada una de las nueve cifras una vez, y sólo una vez, en cada caso.

Dudeney da las soluciones para esos números que plantea, por ejemplo, para 13 sería el número mixto 9 5.472/1368 = 13, aunque también puede haber soluciones para otros números menores que 100. Dejamos este rompecabezas sin resolver para las personas que estáis leyendo esta entrada.

Por otra parte, el gran matemático italiano Giuseppe Peano (1858-1932), a quienes muchos relacionan con la curva de Peano o los axiomas de Peano, entre muchas otras aportaciones matemáticas, publicó en 1925 el libro Giochi di aritmetica e problemi interessanti / Juegos aritméticos y problemas interesantes, que contenía la siguiente cuestión interesante relacionada con las expresiones aritméticas pandigitales. Daba las seis formas de expresar 9 como ABCDE/FGHIJ, utilizando las 10 cifras básicas, del 0 al 9 (en tres de ellas F = 0).

Y con estas curiosas fracciones pandigitales concluimos esta entrada del Cuaderno de Cultura Científica.

Bibliografía:

1.- Raúl Ibáñez, La gran familia de los números, Catarata, 2021.

2.- David Singmaster, Sources in recreational mathematics, an annotated bibliography

3.- A. Cyril Pearson, Twentieth Century Standard Puzzle Book (Libro de puzzles estándar del siglo XX), George Routledge & Sons, 1907.

Versión digital en la Librería Gutenberg: The Project Gutenberg EBook of Twentieth Century Standard Puzzle Book, by Cyril Pearson.

5.- Henry E. Dudeney, Amusements in Mathematics, Thomas Nelson and sons,1917 (el original puede verse en la librería Internet Archive).

6.- David Wells, The Penguin Dictionary of Curious and Interesting Numbers, Penguin Books, 1986.

7.- Giuseppe Peano, Giochi di aritmetica e problemi interessanti, Paravia, 1925 (el original puede verse en la librería Internet Archive ).

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

El artículo Fracciones pandigitales se ha escrito en Cuaderno de Cultura Científica.

Las ideas de Max Planck fueron el germen de algunas de las aportaciones más importantes de Einstein a la física. Planck fue el primero en afirmar explícitamente que la energía no es continua, sino que está constituida por trocitos indivisibles llamados cuantos, una idea sobre la que Einstein se basó para afirmar que la luz también estaba formada por paquetes similares, hoy conocidos como fotones. Esta relación paterno-filial se extendió también al mundo académico: los dos hombres estaban muy próximos y el aliento de Planck fue una gran ayuda para la ciencia y la carrera de Einstein, ya que Planck adoptó un papel muy activo tanto en la promoción de la teoría de la relatividad como en conseguir que Einstein avanzase profesionalmente.

Albert Einstein recibe la Medalla Max Planck de manos de…Max Planck (1929). Era la primera vez que se entregaba la distinción creada por la Sociedad Alemana de Física; se otorgó en esta primera edición a los dos teóricos. El primero en recibirla fue Max Planck, quien, acto seguido, hizo entrega de la suya a Einstein. Fuente: Institute for Advanced Study.

La principal contribución a la física de Max Planck llegó en 1901, cuando resolvió un problema conocido hoy como la “catástrofe del ultravioleta” (este nombre se lo dio Ehrenfest en 1911). Los físicos habían descubierto que cuando se trataba de luz y radiación las leyes de la mecánica clásica de Newton simplemente no servían. Un ejemplo es la llamada radiación del cuerpo negro. Un cuerpo negro es un cuerpo que absorbe toda la radiación electromagnética que incide sobre él que, a su vez, emite en forma de radiación térmica, cuyo espectro puede medirse. Pero la mecánica newtoniana predecía que las longitudes de onda ultravioletas deberían aumentar infinitamente, algo que no parecía probable y que los experimentos desmentían. Planck, que era muy creativo desde el punto de vista matemático, propuso una solución que partía de la hipótesis de que la luz sólo podía existir en paquetes específicos, cuantos, de energía. En vez de tener una onda continua de energía, como una onda sonora, Planck sugería que la energía era discontinua. La idea era parecida a una ola del mar que está compuesta por diminutas moléculas de agua, incluso si no son visibles al ojo humano. Una vez introducidos los cuantos la teoría modificada sí se correspondía con los datos experimentales de la radiación del cuerpo negro. La catástrofe del ultravioleta dejó de ser un problema, nacía la mecánica cuántica.

Pero Planck no sabía muy bien cómo interpretar esta nueva descripción de la radiación, o ni siquiera cómo esta innovadora técnica matemática podría ser aplicada a otra situación. De hecho llegó a decir que había introducido los cuantos en “un acto de desesperación”, por el que ganaría el premio Nobel en 1918. Pero fue un revolucionario reticente y no dio el siguiente paso: intentar averiguar qué significaba esta nueva idea.

Eso quedó para Einstein. Años después, Einstein recordaría que leyó el artículo revolucionario de Planck mientras estaba en la universidad y que dejó una profunda huella en él. Einstein se dio cuenta de que ninguna de las dos teorías fundamentales del momento, la mecánica newtoniana y la teoría electromagnética de Maxwell, describían exactamente el universo. Einstein empleó buena parte de los años siguientes en tratar de resolver este problema. Como consecuencia de este trabajo, en 1905, incorporó las ideas de Planck a una teoría completamente nueva de la luz. La teoría de Einstein decía que la luz visible, igual que la ultravioleta, estaba formada por cuantos. Este concepto fue el que terminó dándole el premio Nobel, pero también fue la teoría que tardó más tiempo en ser aceptada. Al principio, igual que la pasó a Planck antes que a él, Einstein no afirmaba rotundamente que estos “cuantos de luz” fuesen algo más que una herramienta matemática. Sin embargo, pasados unos años llegó a creer realmente que la luz estaba constituida por partículas igual que eran los electrones.

Planck, el facilitador

Es mérito de Planck haber sido uno de los responsables de que el novedoso artículo de Einstein se publicase. Planck era uno de los editores de la prestigiosa revista alemana Annalen der Physik. Llevaba su sección con una increíble apertura de mente: si un autor había publicado antes tenía prácticamente garantizado que podría volver a publicar en la revista, independientemente de lo que Planck opinase personalmente del trabajo. En este caso, a Planck no le gustaba demasiado la nueva teoría, pero movió hilos para que se publicase.

Einstein veía, como no podía ser de otra manera, las raíces de su trabajo en el previo de Planck, pero a Planck le llevó un tiempo poder aceptar la idea. Justo después de la primera Conferencia Solvay, celebrada en el otoño de 1911, Einstein escribió a un amigo: “He tenido bastante éxito a la hora de convencer a Planck que mi concepción [de los cuantos de luz] es correcta, después de su lucha en contra de ella de tantos años”. Si bien Planck terminó aceptando la existencia de los fotones, siempre mantuvo algo de distancia con la física cuántica que él había generado, dejando a sus colegas más jóvenes que trabajasen en los detalles.

Sin embargo, con la teoría especial de la relatividad Planck mantuvo una posición mucho más favorable y activa. El mismo año en que Einstein publicó su teoría de los cuantos de luz, también publicó su artículo sobre la teoría especial de la relatividad. Ese mismo otoño Planck ya daba conferencias sobre los detalles de la nueva teoría de Einstein. Planck era, ya en esa época, un científico de enorme influencia y para el joven Einstein contar con su apoyo fue un éxito importantísimo. En 1910, Planck fue aún más lejos en su apoyo a Einstein, llegando a compararlo públicamente con Copérnico, diciendo. “Este principio [de la relatividad] ha traído una revolución en nuestra representación física del mundo, que, en extensión y profundidad, solamente puede ser comparada con la que produjo la introducción del sistema copernicano”.

Y, con todo y como buen camarada, Planck no podía evitar mofarse educadamente de Einstein: tras leer un intento de éste de escribir un artículo de divulgación de la teoría de la relatividad dirigido al público en general, Planck dijo que Einstein parecía pensar que podía convertir una frase compleja en algo entendible simplemente introduciendo frecuentes interjecciones de “querido lector”.

Planck, el héroe

Planck se convirtió en un defensor de las ideas y la persona de Einstein, llegando a extremos que rayan el heroísmo. Empezando por su carrera profesional, Planck ayudó a Einstein a conseguir un trabajo en los recientemente creados Institutos Kaiser Wilhem en Berlín, llegando a negociar en su favor para que le concedieran los aumentos de sueldo anuales. Planck también era secretario de la Academia Prusiana de Ciencias en la que se dedicaba a promover la ciencia alemana. Al aumentar el nacionalismo y el antisemitismo alemanes, Einstein le prometió a Planck, para entonces un íntimo amigo, que no abandonaría Berlín si no era absolutamente necesario.

Einstein terminaría abandonando Berlín y renunciando a su pertenencia a la Academia Prusiana en 1933, justo después de que se le otorgasen a Hitler plenos poderes sobre Alemania. Para entonces Planck tuvo que admitir que era “la única salida”, pero no se quedó callado como muchos de sus colegas. Permaneció en Alemania y mantuvo su posición en la Academia desde la que intentó desesperadamente contener los ataques contra la “ciencia judía” y los científicos judíos. Tras la marcha de Einstein en 1933, Planck continuó alabando en público su trabajo y a su persona, a pesar de haberse convertido Einstein en el objetivo principal de los ataques y del riesgo que ello suponía para el propio Planck y su familia: “Herr Einstein no es uno más entre muchos físicos sobresalientes, sino que Herr Einstein es el físico a través de cuyos ensayos, publicados en nuestra Academia, el conocimiento físico en este siglo ha sido profundizado de una manera cuya importancia sólo puede compararse con los logros de Johannes Kepler o Isaac Newton”. Planck, llegó a solicitar y conseguir entrevistarse con Hitler para intentar convencerle, sin éxito, de que su política contra los judíos perjudicaba el avance científico alemán.

Tras una vida de prestigio en Alemania, la Segunda Guerra Mundial fue, en lo personal, devastadora para Planck. Su hijo fue asesinado por la Gestapo por su participación en el intento de atentado contra Hitler de 1944. Otros tres hijos de Planck y su primera esposa habían muerto ya y este fue el mazazo final. Le quedaban aún se segunda mujer y el hijo de ambos, pero la vida dejó de interesarle. Moriría tres años después.

Si bien siempre fue un líder de la comunidad científica internacional, Planck no publicó ningún artículo relevante desde el de 1901. Sus escritos se volvieron cada vez más hacia la filosofía de la ciencia y a la descripción de cómo cambiaban las teorías científicas: “Una nueva verdad científica no triunfa porque convence a sus opositores y les hace ver la luz, sino más bien porque sus opositores terminan muriendo y una nueva generación crece familiarizada con ella”. Planck escribía esto en una época en la que otros filósofos estaban desarrollando ideas sobre cómo se desarrolla la ciencia, ideas que todavía perviven en el pensamiento filosófico actual, pero el principio de Planck parece que es especialmente relevante para la mecánica cuántica. Einstein y Planck fueron dos de los pocos físicos que levantaron su voz en contra de la nueva física, mientras que una nueva cosecha de veinteañeros la abrazaba con entusiasmo. Tras las muertes de Einstein y Planck, la mecánica cuántica que fundaron, pero siempre cuestionaron, se enseña, con la convicción de la teoría aceptada, a las nuevas generaciones de estudiantes.

Para saber más:

Las constantes de Planck y el caballo blanco de Santiago

Átomos (serie sobre el descubrimiento de la estructura atómica)

Cuantos (serie sobre la creación de la mecánica cuántica)

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

Una versión anterior de este artículo se publicó en Experientia Docet el 26 de septiembre de 2010.

El artículo Einstein y Max Planck se ha escrito en Cuaderno de Cultura Científica.

Las misiones espaciales nos permiten estudiar el resto de los cuerpos de nuestro Sistema Solar, aunque a veces sea únicamente desde su órbita, pero lo suficiente como para descubrir detalles importantes sobre su estructura y composición, detalles que, desde la Tierra, debido a su lejanía, son muy difíciles de apreciar.

Algunos de los objetos más interesantes dentro del estudio de la geología planetaria son los asteroides, el material «sobrante» de la formación del Sistema Solar. En ellos podemos encontrar reflejados distintos momentos evolutivos, como fósiles que nos muestran las distintas etapas de la construcción de los planetas, con una gran diversidad que va desde los asteroides más primitivos y sin alterar hasta aquellos que podrían haber formado parte de cuerpos mucho más grandes, pero que a causa de los impactos sufrieron una fragmentación catastrófica.

De ahí que su estudio sea tan relevante, porque podríamos encontrar pistas que nos ayudasen a reconstruir todas las etapas de la formación de nuestro sistema planetario, especialmente aquellas que pueden no haber quedado preservadas en los planetas o satélites por todos los cambios que han sufrido a lo largo de 4500 millones de años de historia.

Psique observado desde el Very Large Telescope. Aunque la resolución debido a la distancia no es muy grande, se pueden apreciar importantes variaciones en su albedo (proporción de luz incidente que se refleja). Fuente: ESO/LAM.

Una de las piezas de este puzle podría ser el asteroide 16 Psique, descubierto en 1852 por el astrónomo italiano Annibale de Gasparis, quien descubrió al menos otros nueve asteroides más. Este cuerpo, de unos 226 kilómetros de diámetro, llamó la atención de los astrónomos por como reflejaba la luz del Sol, en una proporción mucho más alta que otros asteroides, haciéndoles pensar que en realidad era un cuerpo principalmente metálico.

¿Y dónde podemos encontrar la mayor parte de los elementos metálicos que forman un planeta? Pues en el núcleo de estos, ya que, durante la etapa de diferenciación planetaria, los planetas todavía a muy alta temperatura empiezan a separar sus componentes químicos por densidad, hundiéndose los elementos más densos y ascendiendo los menos densos, dando lugar a la estructura por capas y la formación del núcleo metálico.

¿Cómo podría ser, entonces, que Psique fuese un cuerpo eminentemente metálico? Al principio, los científicos supusieron que podría ser el núcleo de un planeta que había sufrido colisiones tan violentas que habían arrancado la corteza y una gran parte del manto, dejando expuesto ese núcleo metálico que ahora se observaba. Pero la historia no acababa aquí.

Los estudios sobre su masa y densidad, en cambio, contaban una historia muy diferente: la densidad media estaba en torno a los 4 g/cm3, muy alejado de lo que sería un asteroide monolítico formado por metales. Las perturbaciones gravitatorias que ejercía sobre otros cuerpos cercanos corroboraban ese dato de densidad, por lo que no podía ser exclusivamente un cuerpo metálico o al menos monolítico.

¿Cómo era posible esa discrepancia tan importante entre los datos visuales y los de su masa? Pues era francamente difícil reconciliarlos: algunos autores comenzaron a pensar que podría ser un cuerpo muy poroso debido a los impactos, superando el 50% de porosidad. Esta porosidad podría haber sido la responsable de la baja densidad, pero los modelos físicos hasta el momento consideran poco probable que esto hubiese ocurrido.

Otras teorías apuntaban que podría ser el resultado de varias colisiones en las cuales se mezclase el componente rocoso y metálico de distintos cuerpos, generando una superficie mixta y variada.

Y desde luego, las últimas observaciones de radar muestran que es un cuerpo formado por una mezcla de componentes rocosos y metálicos, lo que parece que es el hecho responsable de que su densidad sea lo baja que parecen mostrar los demás datos, pero, si es así, ¿cómo está formado realmente?

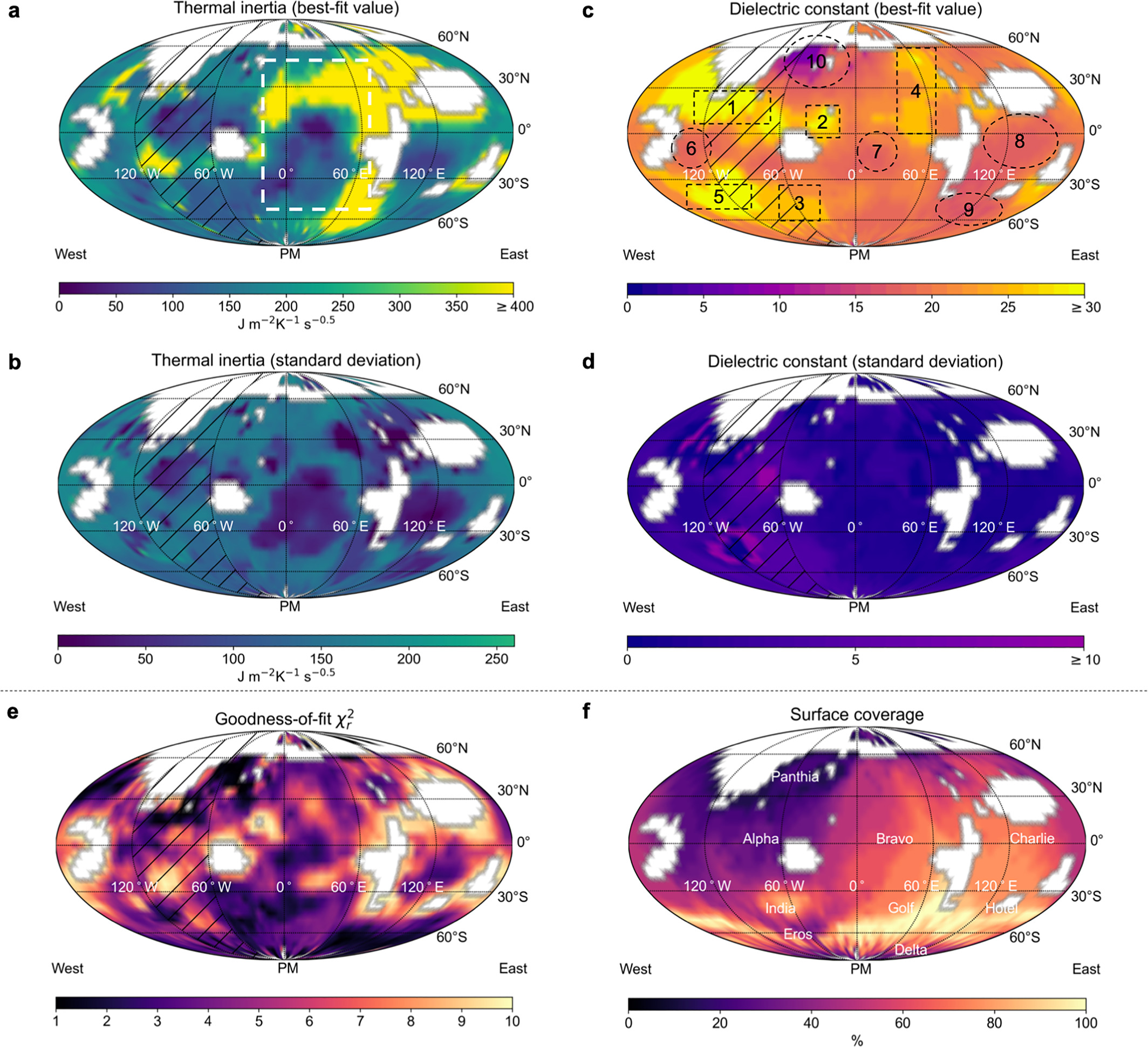Los datos de ALMA sugieren una superficie muy heterogénea, probablemente como fruto de una historia muy compleja. Imagen cortesía de Cambioni et al. (2022).

Uno de los modelos más recientes afirma que, en realidad, Psique es un cuerpo diferenciado, con su corteza y mantos probablemente rocosos… como por ejemplo nuestro planeta. Pero aquí es donde viene lo interesante. Es posible que, tras su formación, Psique tuviese una gran actividad geológica fruto de su calor interno, parte de la cual se traduciría en fenómenos volcánicos.

Estos volcanes podrían haber emitido una lava metálica que provendría del núcleo de Psique, cubriendo parte de la superficie y dando ese aspecto tan reflectante que llamó la atención de los científicos. Eso no quiere decir que antes no hubiese lavas con un componente más silicatado, por ejemplo, simplemente que puede haber otro tipo de vulcanismo que en nuestro planeta no conocemos, por exótico que nos parezca.

De hecho, para comprobar esta hipótesis, un equipo de científicos ha fundido basaltos ricos en hierro, esperando que se segregasen por densidad los distintos elementos. Posteriormente, simularon una erupción para ver qué tipo de relieves podrían generarse en Psique a causa de la interacción entre coladas de lava “rocosas” y las metálicas, pero también las formas que estas lavas podrían generar independientemente sobre la superficie, para que cuando podamos ver la superficie de cerca podamos interpretar de la mejor manera lo que observamos.

No obstante, cabe la posibilidad que la historia de Psique sea todavía más compleja y que los modelos propuestos no sean más que capítulos en la agitada historia de un asteroide que puede ayudarnos a comprender mucho más sobre el nacimiento de nuestro Sistema Solar.

Ilustración de la misión Psique. Fuente: NASA/JPL-Caltech/ASU.

Desgraciadamente, el pasado día 24 de junio se retrasó la misión que debía visitar este asteroide, llamada Psique también y que tenía que despegar este año, hasta, probablemente, 2023 o 2024, por lo que tendremos todavía que esperar a acercarnos a este mundo tan apasionante.

Referencias:

Soldati, A., Farrell, J. A., Wysocki, R., & Karson, J. A. (2021). Imagining and constraining ferrovolcanic eruptions and landscapes through large-scale experiments. Nature Communications, 12(1). doi: 10.1038/s41467-021-21582-w

Matter, A., Delbo, M., Carry, B., & Ligori, S. (2013). Evidence of a metal-rich surface for the Asteroid (16) Psyche from interferometric observations in the thermal infrared. Icarus, 226(1), 419–427. doi: 10.1016/j.icarus.2013.06.004

Cambioni, S., de Kleer, K., & Shepard, M. (2022). The Heterogeneous Surface of Asteroid (16) Psyche. Journal of Geophysical Research: Planets, 127(6). doi: 10.1029/2021je007091

Para saber más:

Choques de asteroides, arte islámico y cuasicristales
De guijarro a asteroide en una trampa de polvo

Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.

El artículo Rumbo a Psique se ha escrito en Cuaderno de Cultura Científica.

Foto:  StockSnap / Pixabay

En promedio, dedicamos una quinta parte de nuestro tiempo de vigilia a relacionarnos con los demás. Pasamos alrededor de tres horas y media al día con otras personas en contextos sociales. Aunque ese tiempo puede parecernos mucho, lo cierto es que no lo es tanto, máxime si tenemos en cuenta con cuántas personas nos relacionamos habitualmente.

Hace ya unos cuantos años, Robin Dunbar propuso que el número aproximado de personas con el que nos relacionamos de forma habitual es de ciento cincuenta (el llamado número de Dunbar). En esa cifra se incluyen las personas con las que nos relacionamos en casa, el trabajo o la calle, y también aquellas con las que interactuamos en las redes sociales de internet.

Ahora bien, no nos relacionamos con todas ellas del mismo modo. Hay diferentes niveles de interacción. Las relaciones pueden, de hecho, visualizarse en una estructura de esferas concéntricas. En la más interna se encuentra la familia o, dependiendo de los casos, el núcleo de apoyo, el puñado de personas que ayudan en los momentos difíciles. Ese grupito lo forman alrededor de cinco personas. No obstante, quienes tienen una familia grande tienden a tener menos amistades cercanas y ocurre lo contrario con quienes no tienen apenas familiares. Otras diez personas, en promedio, son las amistades más cercanas. Treinta y cinco personas más son las que consideramos amigos o amigas. Y las cien que quedan hasta los ciento cincuenta, son las conocidas con las que tenemos trato frecuente.

Si hacemos el cálculo simple de dividir las tres horas y media entre las ciento cincuenta personas con las que nos relacionamos, obtenemos, en promedio, cerca de minuto y medio con cada una de ellas. Pero ese dato, en realidad, no dice gran cosa. El 40% del tiempo que dedicamos a relacionarnos con los demás, lo empleamos con el círculo más próximo. Eso significa que a cada una de esas personas le dedicamos unos diecisiete minutos al día. Igualmente, al grupo de buenos amigos le dedicamos el 20% del tiempo o, lo que es lo mismo, algo más de cuatro minutos diarios a cada uno. Por último, a cada una de las personas de las dos últimas esferas le dedicamos algo más de medio minuto diario.

A la hora de valorar esos datos, hay que tener en cuenta dos cosas. Por un lado, sobre todo en el caso de las personas pertenecientes a la categoría de amigos y conocidos, es muy normal que no se interactúe con ellos todos los días. Pueden pasar semanas, incluso, sin que se mantenga una conversación. Por lo tanto, en las ocasiones en que se mantiene, el tiempo de interacción puede ser bastante más largo. Por otro lado, muchas de esas interacciones no se desarrollan cara a cara, sino a distancia, ya sea por teléfono, mediante mensajería instantánea o a través de redes sociales de internet.

Otro elemento importante es la distancia a la que nos encontramos de todas esas personas. En este aspecto opera la regla de la media hora, el tiempo durante el que estamos dispuestos a desplazarnos para estar con alguna persona de nuestros círculos. Pero, curiosamente, la frecuencia con la que interactuamos a distancia con alguien es mayor cuanto más cerca de nosotros vive.

Por último, las relaciones cambian a lo largo de la vida: las personas entran o salen de esas esferas. Cuanto mayor sea la frecuencia con la que nos relacionamos con alguien, más probable es que la relación se prolongue. Por eso, si queremos que una relación se mantenga, conviene que la cultivemos. No sobrevive sin atención.

Fuente: Robin Dunbar (2021): Friendship-ology. New Scientist 249 (3324): 36-40.

Para saber más:

Nos relacionamos con ciento cincuenta personas 

 

Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU

El artículo Familiares, amigos, amigas y personas conocidas se ha escrito en Cuaderno de Cultura Científica.

¿Estamos realmente diseñados para conectar con los demás? Si es así, ¿por qué siguen existiendo los psicópatas? ¿Se pueden tratar trastornos delirantes como la paranoia desde el punto de vista de la evolución? O ¿cómo ha cambiado la atracción sexual desde la época de nuestros ‘abuelos’ homínidos hasta ahora?

A estas y otras cuestiones relativas a la evolución del comportamiento humano se trató de dar respuesta durante la IV Jornada Nacional de Evolución y Neurociencias, evento organizado por la Cátedra de Cultura Científica de la UPV/EHU y la Red de Salud Mental de Bizkaia, que tuvo lugar los días 28 y 29 de abril en el Bizkaia Aretoa – UPV/EHU de Bilbao.

Desde que en 2017 un grupo de psiquiatras de la Red de Salud Mental de Bizkaia organizara la primera edición de esta jornada, la cita se ha convertido en un punto de encuentro para profesionales de distintos ámbitos científicos como la psiquiatría, la psicología, la biología o la filosofía con un interés común: la conducta humana desde una perspectiva evolucionista y su divulgación científica en un formato accesible y ameno para todos los públicos, a la par que riguroso y actualizado.

El cerebro humano es una máquina especializada en desentrañar mentes. Y lo hace casi siempre inconscientemente, de manera rápida y eficaz. ¿Cómo? Sintiendo lo mismo que los otros. El cerebro humano es hipersocial y emocional mucho más que racional. Nos los cuenta Manuel Martín Loeches, catedrático de psicobiología de la Universidad Complutense de Madrid y responsable de la Sección de Neurociencia Cognitiva del Centro Mixto UCM-ISCIII de Evolución y Comportamiento Humanos.



Para saber más:

El gran encéfalo humano es un “encéfalo social”
Nuestro cerebro no piensa (y el de usted, tampoco)

Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus

El artículo IV Jornada Nacional de Evolución y Neurociencias: Manuel Martín Loeches – Carácter emocional e hipersocial del cerebro se ha escrito en Cuaderno de Cultura Científica.

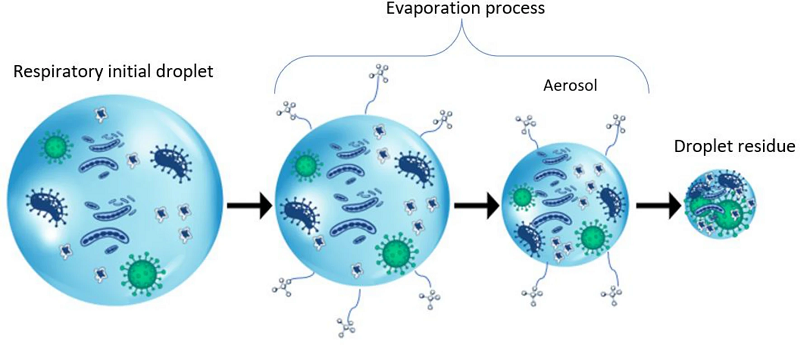
La capacidad de transmisión de un virus es uno de los factores más importantes a tener en cuenta en el estudio de enfermedades infecciosas. La gran mayoría de virus se transmiten por vía oral. Cuando una persona tose, habla o estornuda, exhala al ambiente una serie gotas de saliva que contienen el virus y, por tanto, tienen una gran capacidad de contagio. El tiempo que estas gotas van a permanecer en el aire depende de la velocidad de evaporación que, a su vez, depende de diferentes variables. Estas variables, en consecuencia, afectan a la transmisión del virus. Como se suponía, y ahora se confirma, temperatura y humedad son las más relevantes.

“El objetivo de este trabajo es estudiar mediante simulaciones computacionales el comportamiento de una partícula de saliva expuesta a diferentes características ambientales de un entorno social”, señalan Ainara Ugarte Anero y Unai Fernández Gamiz, investigadores del Departamento de Ingeniería Nuclear y Mecánica de Fluidos de la UPV/EHU, en la Escuela de Ingeniería de Vitoria-Gasteiz.

Para estudiar cómo se comporta la gota de saliva a través del aire, los investigadores crearon una simulación computacional basada en la dinámica de fluidos (CFD-Computational Fluid Dynamics) que examina el estado de una gota de saliva que se mueve por el aire cuando una persona habla, tose o estornuda. “Esta simulación se realizó en un entorno controlado y simplificado, es decir, en lugar de analizar un estornudo general con una serie de partículas, nos centramos en el estudio de una sola partícula en un entorno cerrado. Para ello, lanzamos gotas de entre 0 y 100 micras de una altura de unos 1,6 metros —distancia a la que se encuentra más o menos la boca de un humano— y se consideraron los efectos de la temperatura, la humedad y el tamaño de la gota”, explica Unai Fernández Gamiz.

“Los resultados demuestran que la temperatura ambiente y la humedad relativa son parámetros que afectan significativamente al proceso de evaporación. El tiempo de evaporación tiende a ser mayor cuando la temperatura ambiente es menor. Y las partículas con menor diámetro se evaporarán rápidamente, mientras que a las de mayor diámetro les cuesta más. Algunas partículas grandes, de alrededor de 100 micras, pueden permanecer en el ambiente entre 60-70 segundos y en principio se transportan a una mayor distancia; por lo tanto, por ejemplo, puede que una persona estornude en un ascensor, salga del ascensor y las partículas sigan ahí. De ahí la importancia de la distancia de los dos metros de distancia de seguridad en entornos cerrados en el caso de la COVID-19. Según lo estudiado, parece que esa distancia puede resultar razonable para evitar más contagios en el caso de la Covid-19”, indica la primera autora del trabajo.

A esto hay que sumarle también la humedad. “En un ambiente húmedo la evaporación se produce más lentamente, por lo que el riesgo de contagio es mayor, ya que las partículas permanecen más tiempo en suspensión”, añade Ugarte.

Referencia:

Ainara Ugarte Anero, Unai Fernandez Gamiz, Koldo Portal Porras, Ekaitz Zulueta y Oskar Urbina Garcia (2022) Computational characterization of the behavior of a saliva droplet in a social environment Scientific Reports doi: 10.1038/s41598-022-10180-5

Para saber más:

Saliva, bacterias y oxitocina: ¿por qué nos gusta tanto besarnos?
Lo que funciona, y lo que no, contra la Covid-19

Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa

El artículo El comportamiento social de una gota de saliva se ha escrito en Cuaderno de Cultura Científica.

Una de las principales características que definen la saga de videojuegos de Silent Hill es su atmósfera. Para crear ese ambiente psicológicamente opresor típico de cualquier survival horror que se precie, aquí nos encontramos perdidos en un pueblo cubierto por una espesa niebla que te impide discernir si lo que tienes a escasos metros de distancia es un poste de teléfonos o un ser horrendo que no pretende darte un abrazo, precisamente. Cuando Silent Hill se llevó a la gran pantalla en 2006, el equipo técnico que desarrolló el film cambió ligeramente la historia original, haciendo que la protagonista se perdiera por un pueblo fantasma sobre el que cae, de manera constante, una fina lluvia de ceniza que lo envuelve todo con un manto grisáceo. Y le dan una explicación basada en hechos reales que, aunque no os lo creáis, tiene una base geológica, como no podía ser de otra manera.

Detalle de la carretera de entrada a la localidad de Centralia, Pensilvania, donde se observan diversas fracturas a través de las que surge el humo producido por la combustión del carbón subterráneo. Foto: JohnDS / Wikimedia Commons.

Para ello debemos viajar a un pueblecito bucólico de Pensilvania, Estados Unidos, llamado Centralia. Nacido a mediados del siglo XIX gracias al descubrimiento de importantes yacimientos de carbón en toda la zona, la industria minera y extractora de este material se convirtió en su principal impulso económico. Pero, a comienzos de la década de los sesenta del siglo pasado, todo se convirtió en una pesadilla, al más puro estilo de las introducciones de los videojuegos de terror. Se produjo un incendio en una de las antiguas minas que alcanzó una de las vetas superficiales de carbón y el fuego se extendió sin control por todas las minas excavadas por debajo de la ciudad. Se abrieron grietas por el pavimento que se tragaban todo lo que pillaban por su camino, los depósitos subterráneos de combustible de la gasolinera alcanzaron temperaturas que presagiaban tremendas explosiones y surgieron gases tóxicos, humo y una lluvia constante de ceniza que empezó a cubrir toda la ciudad. Se intentó sofocar el incendio en múltiples ocasiones, pero todas infructuosas, porque mientras haya carbón bajo la tierra, el fuego permanecerá incontrolable durante décadas, incluso, siglos. A día de hoy, Centralia es un pueblo fantasma en el que apenas permanecen un puñado de habitantes.

Cartel turístico junto al cementerio de la Iglesia de San Andrew, en Birmingham. El texto dice: El carbón sobre el que se asienta la Iglesia de San Andrew era muy volátil. Era habitual que el carbón entrara en combustión bajo tierra, emitiendo humo y llamas por el cementerio. Parecían “los fuegos del Infierno”. Foto: Marta Pascual.Fuegos fatuos de base geológica

Nos toca ahora cambiar de continente para conocer otra historia muy similar y también bastante tétrica. Para ello, debemos desplazarnos a la ciudad inglesa de Birmingham, la segunda más poblada del Reino Unido y cuna de la Revolución Industrial a mediados del s. XVIII debido a que se asienta en una zona con una abundante acumulación de depósitos de carbón. A las afueras de la ciudad encontramos una pequeña colina en cuya cima construyeron la Iglesia de San Andrew, con un cementerio con las tumbas excavadas en la tierra y las lápidas de piedra. Pues esa colina tiene niveles de carbón muy rico en gases inflamables que afloran casi en superficie, hasta el punto de que la caída de un rayo provoca que se prendan fuego. Y los gases, humo e incluso llamas resultantes de la combustión salen a la superficie… entre las lápidas del cementerio. Obviamente los habitantes de Birmingham de hace un par de siglos debían creer que se encontraban a la entrada del infierno cuando veían esto. Eso, o en la mismísima Racoon City de Resident Evil.

Reconstrucción de una zona pantanosa bordeada por bosques de helechos arborescentes, licopodios, equisetos y coníferas de finales del Carbonífero. Ilustración: Sergey Krasovskiy.

Pero la interrelación entre los depósitos de carbón estadounidenses y británicos no se queda en una mera anécdota terrorífica. El carbón es una roca sedimentaria de origen orgánico, formada por restos vegetales continentales acumulados y enterrados en zonas pantanosas o estuarinas y que han sufrido una descomposición en ausencia de oxígeno. Tras el paso de millones de años y debido a la compactación por enterramiento, esta materia orgánica termina por consolidarse, dando lugar a las rocas sedimentarias. Estas rocas, formadas principalmente por carbono, son capaces de generar energía por combustión, por lo que se emplean como combustible fósil desde hace milenios. Los principales depósitos de carbón se han formado a partir de los restos vegetales que poblaron los pantanos y el litoral de nuestro planeta a finales de la Era Paleozoica, en un Periodo geológico ocurrido hace entre unos 359 y 299 millones de años. Y el nombre de ese Periodo fue acuñado por dos geólogos británicos a comienzos del siglo XIX estudiando las rocas que afloraban en su tierra. Como no podía ser de otra manera, lo llamaron Carbonífero, del latín “portador de carbón”. Pues siguiendo con la tradición geológica de subdividirlo todo, en Estados Unidos partieron en dos mitades al Periodo Carbonífero y, a la parte final del mismo (desde hace unos 323 a 299 millones de años), la denominaron Pensilvaniense en honor al estado de Pensilvania por la enorme abundancia de depósitos de carbón de esa zona. Y si aún queréis unir más a las ciudades de Birmingham y Centralia, a finales del Carbonífero Norteamérica y las Islas Británicas formaban parte de una misma masa continental, Laurrusia, a lo largo de la cual se desarrollaron las enormes masas vegetales que circundaban extensos pantanos bajo un clima subtropical y que, millones de años después, dieron lugar a los depósitos de carbón explotados en ambas localidades.

No siempre es fácil verlo, pero la Geología impregna por completo todo nuestro sesgo cultural, independientemente de la época en la que nos encontremos. Así, una curiosidad geológica puede convertirse tanto en una leyenda demoníaca como en inspiración para la ambientación terrorífica de una película basada en un videojuego. Lo más divertido es buscar el origen científico de todo ello.

Para saber más:

Una extinción de novela policiaca

Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU

El artículo Historias (geológicas) de la cripta se ha escrito en Cuaderno de Cultura Científica.

No es sencillo dedicarse a la investigación cuando, por necesidades familiares, los cambios de domicilio son continuos, y a lugares con culturas diversas. No es fácil pasar de las matemáticas abstractas a las aplicadas. Mary Wynne Warner brilló como investigadora a pesar de sus obligaciones como “esposa de un diplomático”, de ser madre de dos hijas y un hijo, y de tener que cambiar de la topología algebraica a la topología difusa. ¿Su receta? Talento, capacidad de adaptación y un admirable empeño.

Mary Wynne Warner. Fuente: 100WelshWomen.

 

Mary Wynne Davies nació el 22 de junio de 1932 en Carmarthen, en el sur de Gales. Su madre se llamaba Esther (1899-1982) y su padre Sydney (1901-1978); Mary era la mayor de las dos hijas del matrimonio. Cuando Mary tenía 6 años, la familia se mudó a Llandovery; el padre había sido nombrado director de una escuela primaria, a la que Mary asistió como alumna, una alumna muy destacada.

Estaba decidida a estudiar matemáticas, y en 1951 ingresó en la Universidad de Oxford para cumplir su sueño, graduándose en 1953. Obtuvo una beca de investigación para realizar su trabajo de doctorado en Oxford. Su supervisor fue el conocido matemático Henry Whitehead (1904-1960), quien lideraba un grupo muy activo en topología algebraica. Mary se incorporó a este equipo, y realizó grandes progresos en su investigación. En 1956 publicó su primer trabajo, A note on Borsuk’s antipodal point theorem, en la revista Oxford Quarterly Journal of Mathematics.

Un doctorado fallido y otro diez años más tarde

Lamentablemente, Mary no completó su doctorado bajo la supervisión de Whitehead. Había conocido a un estudiante de historia en Oxford, Gerald Warner, quien se graduó en 1954 y se unió al Servicio Diplomático en la Rama de Inteligencia. Cuando le destinaron a China, Mary y Gerald decidieron casarse. Lo hicieron en 1956, y poco después partieron hacia Beijing.

La vida de Mary cambió radicalmente, su apellido pasó a ser Warner, era la esposa de un diplomático, terminar la tesis no era posible lejos de Oxford y con sus nuevos compromisos. Aunque no renunció a las matemáticas: en Beijing conoció al topólogo chino Chang Su-chen, otro discípulo de Whitehead.

Sus reuniones de trabajo duraron poco tiempo. China estaba sufriendo un profundo cambio; entre 1955 y 1957, Mao Zedong impulsó el movimiento Sufan y el movimiento antiderechista: más de medio millón de personas fueron perseguidas, la mayoría intelectuales y disidentes. Chang Su-chen le comunicó a Mary que sus reuniones para hablar de matemáticas resultaban sospechosas para su gobierno y podían causarles graves problemas. Las matemáticas terminaron en 1958 en Beijing, año en el que nació la primera hija de los Warner, Sian. Poco después, la familia regresó a Inglaterra.

En Londres, Mary fue contratada como profesora a tiempo parcial en el Bedford College. En 1959, y en Reino Unido, nació su segundo hijo, Jonathan. Al poco tiempo Gerald fue destinado a Birmania. Allí, en Rangún, nació su tercera hija, Rachel, en 1961. Y Mary fue contratada como profesora en la Universidad de Rangún.

La familia regresó a Londres por un tiempo y Mary volvió a ocupar su puesto en el Bedford College. En 1964, el trabajo de su marido la llevó a Polonia, donde se unió a la escuela de Karol Borsuk (1905-1982) en Varsovia. Mary Warner comenzó a trabajar en una tesis doctoral bajo la supervisión de Andrzej Białynicki-Birula (1935-2021). Tras dos años en Varsovia, la familia de Mary se trasladó otros dos años a Ginebra durante los cuales completó su tesis doctoral, The homology of Cartesian product spaces, que presentó a la Academia de Ciencias de Polonia. ¡Por fin era doctora en matemáticas!

En 1968, la familia Warner regresó a Londres; Mary fue contratada como profesora de matemáticas en la City University. Al año siguiente apareció su segundo artículo The homology of tensor products. Entre 1974 y 1976, su marido fue destinado a Malasia; fue su último destino fuera del Reino Unido. Allí, en la revista Bulletin of the Malaysian Mathematical Society, Mary publicó sus dos siguientes artículos Some separation axioms weaker than T1(1975) y A note on the reduction of the general equation of a quadratic surface (1976).

Un cambio radical de tema de investigación

Al regresar a Londres, Mary recuperó su trabajo en la City University, y se concentró en la investigación matemática, en particular en la matemática difusa, área de la que se convirtió en una respetada investigadora.

Entre 1980 y 1985, Mary Warner escribió una veintena de artículos sobre espacios de tolerancia y teoría de autómatas. Generalizó ambos conceptos en el ámbito de la teoría de retículos en 1984.

La brillante actividad investigadora de Mary Warner la llevó a ser nombrada catedrática en la City University en 1996. Aunque profesionalmente estos éxitos le proporcionaron grandes alegrías, tardías por todas las dificultades que encontró, su vida privada estuvo rodeada de tragedia. Su hija Sian y su hijo Jonathan se suicidaron en la década de 1990.

Mary se jubiló en 1996, aunque continuó supervisando estudiantes de doctorado y trabajando en su investigación. Falleció inesperadamente, mientras dormía, el 1 de abril de 1998.

Referencias

• J. J. O’Connor and E. F. Robertson, Mary Wynne Warner, Mac Tutor, University of St. Andrews, 2003

• I. M. James and A. R. Pears, Mary Wynne Warner, Bull. London Math. Soc. 34 (2002) 745-752

• Mary Wynne Warner (1932-1998), mathematician, Dictionary of Welsh Biography

• Mary Wynne Warner, 100WelshWomen

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad

El artículo Mary Wynne Warner, la matemática viajera que pasó de la topología algebraica a la difusa se ha escrito en Cuaderno de Cultura Científica.

El meteorólogo ruso Alexander Friedmann fue uno de los primeros científicos en aplicar las ecuaciones de la relatividad de Einstein a un modelo del universo. Friedmann creó un modelo que mostraba un universo en expansión, un modelo que más tarde se probó que es correcto. Pero Einstein rechazó el modelo de Friedmann, llegando a publicar que los cálculos estaban mal hechos. Tuvo que rectificar.

Aleksandr Aleksándrovich Fridman, más conocido en los ambientes como Alexander Friedmann.

Alexander Friedmann* fue testigo de las primeras semillas de una revolución en la cosmología mientras vivía la revolución en Rusia. Nació en San Petersburgo en 16 de junio de 1888 y murió en la misma ciudad con tan solo 37 años, pero ahora la ciudad se llamaba Leningrado. Friedmann, por formación, era meteorólogo y, en sus últimos años bromeaba de vez en cuando diciendo que los matemáticos malos se hacen físicos, y que los físicos malos se hacen meteorólogos. Pero Friedmann tenía poco de mal físico y siempre estuvo a la última en los avances de su ciencia. Su apertura a nuevas ideas se la debió en parte a Paul Ehrenfest, que estableció un seminario de física en San Petersburgo en 1906 al que asistió Friedmann, y con quien desde entonces mantuvo una correspondencia fluida.

En 1920, Friedmann, tras un periodo en la Universidad de Perm, vuelve a su ciudad, entonces llamada Petrogrado, para enseñar matemáticas y física en la Universidad de Petrogrado y en el Instituto Politécnico. La Primera Guerra Mundial (1914-1918) había dejado aislada a Rusia de los últimos adelantos en la física, sobre todo alemana. Friedmann descubre en esta época la teoría general de la relatividad que Einstein había publicado en 1915. Se enseñó a sí mismo relatividad general leyendo directamente los artículos de Einstein, a pesar de que la mayoría de los físicos rusos ignoraron el asunto, y pronto empezó a sacar sus propias conclusiones que fue avanzando por carta a Ehrenfest.

El modelo Friedmann

Usando la relatividad general, Friedmann propuso un nuevo modelo del universo. Creyendo en la belleza y simplicidad perfectas de las matemáticas de Einstein, Friedmann se negó a ajustar las ecuaciones de la relatividad, como hiciese el propio Einstein, para incorporar una arbitraria “constante cosmológica” que permitiese garantizar la estabilidad del tamaño del universo. En vez de eso, el modelo de Friedmann tiene una distribución uniforme de materia. Este universo podría cambiar de tamaño, ya sea expandiéndose o, posiblemente, expandiéndose para luego contraerse para expandirse otra vez, cíclicamente. Un universo que se expande implica un universo que antes ha sido más pequeño. Llevando esto a su conclusión lógica el universo debió haber comenzado como un puntito minúsculo que se hizo mayor con el paso del tiempo. La idea de que el universo comenzó en un solo punto fue lo que más tarde evolucionaría hasta conocerse como teoría del Big Bang, Friedmann fue una de las primeras personas que consideró esta idea (el primero en proponerlo formalmente, sin embargo, fue Georges Lemaître en 1927 basándose, no en las ecuaciones de Einstein, sino en las leyes de la termodinámica).

Friedmann sabía que su modelo era una representación simplificada del universo y que no era la única solución a las ecuaciones de Einstein (de Sitter había publicado uno en el que universo no tenía materia, por ejemplo). Hasta qué punto creía realmente Friedmann que el universo había comenzado en un momento dado no está claro, pero sí es evidente que creía que su modelo era matemáticamente consistente y científicamente interesante, una herramienta más para ayudar a interpretar nuestro mundo. Friedmann publicó su modelo (“Sobre la curvatura del espacio”) en Zeitschrift für Physik en 1922 [1]. Einstein respondió en la misma revista tres meses más tarde con un sólo párrafo: “Los resultados concernientes al mundo no-estacionario, contenido en el trabajo [de Friedmann], me parecen dudosos. En realidad resulta que la solución dada en él no satisface las ecuaciones de campo”.

Friedmann escribió una carta muy cortés a Einstein en la que probaba las bases matemáticas de su trabajo:

“Considerando que la posible existencia de un mundo no-estacionario tiene un cierto interés, me permitiré presentarle aquí los cálculos que he hecho…para verificación y evaluación crítica. […] Si encontrase los cálculos presentados en mi carta correctos, por favor sea tan amable de informar a los editores de Zeitschrift für Physik acerca de ello; quizás en este caso publicará usted una corrección a su afirmación o dará la oportunidad de que una parte de esta carta se publique”.

Sin embargo, para cuando llegó la carta a Berlín, Einstein ya se había marchado de viaje a Japón. No volvería a Berlín hasta marzo, pero no parece que leyese la carta de Friedmann. Solo cuando Krutkov, un colega de Friedmann en Petrogrado, se encontró con Einstein en la casa de Ehrenfest en Leiden en mayo de 1923 y le contó los detalles de la carta de Friedmann, Einstein reconoció su error. Escribió inmediatamente a Zeitschrift für Physik:

“En mi nota previa he criticado [el trabajo de Friedmann sobre la curvatura del espacio]. Sin embargo, mi crítica, al convencerme por la carta de Friedmann que me comunicó el señor Krutkov, estaba basada en un error en mis cálculos. Considero que los cálculos del señor Friedmann son correctos y arrojan nueva luz”.

A pesar de ello, Einstein siguió rechazando la validez del modelo de Friedmann basándose en aspectos más metafísicos. Einstein simplemente no estaba cómodo con la idea de un universo que cambiase con el tiempo. Y no estaba solo; la mayoría de los científicos contemporáneos tenía unas opiniones igual de enraizadas sobre la eternidad del universo, de que sólo podía ser estático y de que sólo podía haber existido durante eones en la forma y tamaño que tenía en ese momento.

En 1924, Friedmann publicó otro artículo (“Sobre la posibilidad de un mundo con una curvatura negativa constante del espacio”) [2] que completaba el de 1922 y con el que demostraba que tenía un dominio de las tres posibles curvaturas del modelo (positiva, nula y negativa) una década antes de que Robertson y Walker publicasen su análisis.

En 1929, cuando Edwin Hubble demostró mediante observaciones astronómicas que el universo se está expandiendo, Einstein aceptó por fin la posibilidad de que el modelo de Friedmann, y el de otros como el suyo, pudiesen ser interpretaciones razonables de la relatividad. Friedmann no viviría para verlo: había muerto en 1925 de fiebre tifoidea. En la actualidad su modelo, completado por las aportaciones posteriores, se conoce como métrica Friedmann-Lemaître-Robertson-Walker.

Referencias:

[1] Friedman, A. (1922). Über die Krümmung des Raumes Zeitschrift für Physik, 10 (1), 377-386 DOI: 10.1007/BF01332580

[2] Friedmann, A. (1924). Über die Möglichkeit einer Welt mit konstanter negativer Krümmung des Raumes Zeitschrift für Physik, 21 (1), 326-332 DOI: 10.1007/BF01328280

Nota:

* Mantenemos la grafía Friedmann por ser la más extendida; firmó sus publicaciones en alemán tanto como Friedman como Friedmann. La transliteración al castellano de su nombre ruso es Aleksandr Aleksándrovich Fridman; de hecho, el cráter lunar en su honor es el cráter Fridman.

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

Una versión anterior de este artículo se publicó en Experientia Docet el 18 de octubre de 2009.

El artículo Einstein y Alexander Friedmann se ha escrito en Cuaderno de Cultura Científica.