Cuaderno de Cultura Científica

Virginia Arechavala trabaja en el grupo de desórdenes neuromusculares del Instituto de Investigación Sanitaria Biocruces Bizkaia. En esta interesante charla presenta su trabajo en busca de nuevas terapias para enfermedades poco frecuentes (habitualmente conocidas como «raras»), especialmente la distrofia muscular de Duchenne.

Virginia se doctoró en neurología en el King’s College de Londres y, tras varios años de investigación en centros británicos, se incorporó a Biocruces como profesora de investigación Ikerbasque.



Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus

El artículo Virginia Arechavala – Naukas Pro 2019: Buscando terapias para enfermedades poco frecuentes se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Francisco Villatoro – Naukas Bilbao 2019: El abrazo de la plata
2. Medicina regenerativa: utilización de células madre para el tratamiento de enfermedades humanas
3. Alfredo García – Naukas Bilbao 2019: Derribando mitos sobre la energía nuclear

La galaxia interna: neuronas (teñidas de rojo) y astrocitos (teñidos de verde) en un cultivo de células corticales de ratón. Fuente: Wikimedia Commons

Es conocida la importancia de la salud de las neuronas y sus conexiones para prevenir la aparición de algunas de las enfermedades neurodegenerativas más comunes, como las de Alzheimer o Parkinson. Sin embargo, las neuronas no están solas en el encéfalo, y muchas de sus funciones están soportadas por otras células, las llamadas células gliales. Entre estas grandes desconocidas se encuentran los astrocitos, las más abundantes y cuyas funciones incluyen desde el aporte de nutrientes y energía a las neuronas hasta el soporte físico de las mismas.

La enfermedad de Parkinson se relaciona con el deterioro de las neuronas de tipo dopaminérgico y con la acumulación de la proteína denominada alfa-sinucleína.

“Hasta ahora, puesto que las células que se ven principalmente afectadas por la enfermedad son las neuronas, la inmensa mayoría de estudios han estado enfocados a comprender los eventos que llevaban a estas células a morir. Es por ello, y puesto que se sabe muy poco del papel de los astrocitos en esta enfermedad, que nosotros decidimos dirigir nuestra investigación a entender si estas células tan importantes para la supervivencia neuronal contribuyen al desarrollo de la enfermedad de Parkinson”, señala Paula Ramos González investigadora del departamento de Neurociencias de la UPV/EHU.

Los investigadores han seguido dos líneas de investigación. Por un lado, “hemos trabajado con células de rata tanto con neuronas como con astrocitos, y pudimos determinar que los astrocitos son capaces de contribuir a la transmisión de la proteína tóxica alfa sinucleina —proteína que se acumula en el cerebro de los pacientes con enfermedad de Parkinson— y favorecer la muerte neuronal, sugiriendo un papel importante de estas células en la progresión de la enfermedad”, explica la investigadora.

Por otro lado, “con el fin de aproximarnos más a la realidad, planteamos un segundo estudio utilizando células humanas. Para ello, generamos astrocitos a partir de células de la piel de pacientes con Parkinson. Una vez generados estos astrocitos, comparamos diversos parámetros importantes entre los astrocitos derivados de donantes sanos y los astrocitos con la mutación. Sorprendentemente, encontramos que los astrocitos con la mutación no sólo eran hasta ocho veces más pequeños que los astrocitos sanos, sino que además generaban elevados niveles de proteínas oxidadas, que pueden resultar tóxicas para las células” añade Ramos González.

Finalmente, “consideramos importante cocultivar estos astrocitos directamente con neuronas, y analizar los efectos que podrían tener las células con la mutación sobre la supervivencia neuronal. Utilizando una técnica que nos permite seguir las neuronas individualmente, observamos que cuando estas convivían con los astrocitos con la mutación, el riesgo de muerte neuronal aumentaba significativamente, contrariamente a lo que ocurría al cultivarlas con astrocitos sanos” comenta.

La investigadora ha destacado que «todos estos resultados sugieren que los astrocitos disfuncionales contribuyen al inicio y progresión de la enfermedad de Parkinson, favoreciendo el proceso neurodegenerativo típico de la enfermedad. Aunque aún es necesario ahondar en el tema y profundizar con nuevos experimentos, este estudio propone una nueva posible diana terapéutica dirigida a mantener la funcionalidad de los astrocitos y abre un abanico de posibilidades en cuanto a futuros posibles tratamientos”.

Referencias:

Cavaliere, F. et al. (2017) In vitro α-synuclein neurotoxicity and spreading among neurons and astrocytes using Lewy body extracts from Parkinson disease brains Neurobiology of Disease doi: 10.1016/j.nbd.2017.04.011

Bengoa-Vergniory, N. et al. (2020) CLR01 protects dopaminergic neurons in vitro and in mouse models of Parkinson’s disease Nature Communications doi: 10.1038/s41467-020-18689-x

Ramos-González, P. (2020) Unraveling the role of astrocytes in the onset and spread of Parkinson’s disease UPV/EHU Tesis doctoral

 

Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa

 

El artículo El papel de los astrocitos en la aparición de la enfermedad de Parkinson se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Una posible terapia neuroprotectora y neurorrestauradora para el párkinson
2. El cannabis rompe el equilibrio metabólico entre neuronas y astrocitos alterando el comportamiento social
3. La mutación vasca de la dardarina y el párkinson

Existen muchos relatos, folclore y mitología relacionados con los grillos, que otorgan distintos significados a su sonido característico. En algunas zonas de Brasil, el canto de los grillos se asocia a la lluvia inminente o a una ganancia financiera inesperada. En otras, también puede ser un presagio de enfermedad. En Caraguatatuba, su significado depende de su color. En Barbados, un grillo ruidoso es señal de dinero, mientras que uno más tímido puede presagiar la enfermedad o incluso la muerte. En nuestra propia cultura audiovisual es común utilizar el sonido de los grillos para enfatizar el silencio, probablemente porque lo asociamos al campo, a las noches tranquilas lejos de la ciudad.

Foto: Aurélien Lemasson-Théobald / Unsplash

El origen de este sonido fue un misterio durante mucho tiempo. Algunas ilustraciones infantiles los muestran tocando pequeños violines. Otro mito persistente es que estos insectos se frotan las piernas para cantar. Ninguna de estas versiones es correcta (aunque me encantaría que la de los violines lo fuera). Lo cierto es que los grillos producen su sonido con ayuda de sus alas. Las frotan entre sí en un proceso conocido como estridulación. En una de las alas se encuentra el llamado “rascador”, con un borde bien definido. Mientras que la otra cuenta con una superficie con ondulaciones llamada “cuerpo”. El efecto es similar al de pasar un dedo por los dientes de un peine y no tan distinto al de deslizar un arco sobre las cuerdas de un violín. Si el traqueteo es lo bastante rápido, da lugar a un tono musical agudo y rugoso, como el canto del grillo, precisamente. Cada especie de grillo cuenta con estructuras distintivas que dan lugar a su timbre único. En el año 2012, un grupo de científicos consiguió incluso recrear el canto de una especie extinta [1], el Archaboilus musicus. Analizando un fósil de 165 millones de antigüedad, con las alas excepcionalmente bien preservadas, determinaron que este grillo o saltamontes jurásico producía un sonido de 6400 Hz.

La mayoría de los grillos hembra carecen de esas estructuras en sus alas por lo que no pueden produir los mismos sonidos. Hay excepciones: algunas hembras de grillos topo cantan. Pero en general, son los machos los que producen este característico timbre. Y, como decía Josquin des Prez, cuando lo hacen es solo por amor: su objetivo es atraer a las hembras y algunos utilizan todo un repertorio de distintas llamadas con este fin. Unas sirven para llamar a sus parejas desde lejos, otras funcionan mejor en las distancias cortas. Cuentan incluso con melodías triunfales para después del apareamiento o cantos cuyo objetivo es intimidar a otros machos. Las hembras, mientras tanto, les escuchan con los pies. No es nada despectivo: los grillos tienen pequeños agujeros en sus patas delanteras, de apenas un milímetro de diámetro. Son uno de los oídos más pequeños del reuno animal, pero también son muy sensibles.

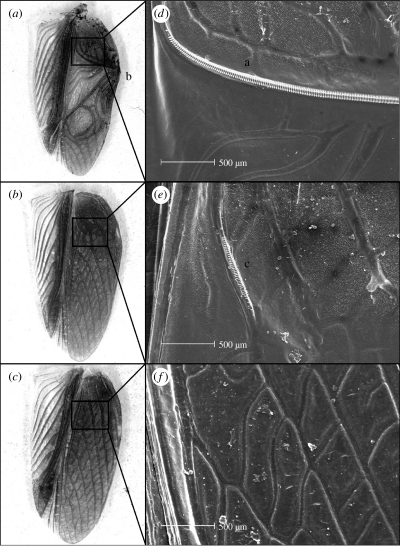Parte inferior del ala de un macho normal (a), un macho de alas planas (b) y una hembra (c). Fuente

Por otra parte, en la isla de Kauai en Hawaii, existe una especie de grillos que se han quedado mudos en apenas veinte generaciones [2][3]. En 2003, Marlene Zuk viajó a la isla y quedó sorprendida por su extraño silencio. Llevaba estudiando a estos bichos desde 1991 cuando su sonido inundaba el paisaje. Pero de año en año, su canto había ido atenuándose, hasta alcanzar un completo silencio apenas 12 años después. Los grillos no habían desaparecido. Pero estaban siendo atacados por una especie de mosca parasitaria que los localiza gracias a su canto. La mosca deja caer su larvas sobre ellos y estas los devoran desde dentro. La nueva presión ambiental ha hecho que en muy poco tiempo, solo sobrevivan los grillos silenciosos, con alas lisas parecidas a las de las hembras de su especie. Lo curioso es que estos grillos siguen frotando sus alas, como solían hacerlo para cortejar a las hembras. Como una orquesta de mimos aplicados, los grillos de Kauai siguen tocando sus violines, aunque ninguno cuente ya con su arco.

Referencias:

[1] Gu, J.-J., Montealegre-Z, F., Robert, D., Engel, M. S., Qiao, G.-X., & Ren, D. (2012, March 6). Wing stridulation in a Jurassic katydid (Insecta, Orthoptera) produced low-pitched musical calls to attract females. PNAS. https://www.pnas.org/content/109/10/3868

[2] Zuk M., Rotenberry J.T., Tinghitella R.M. Silent night: adaptive disappearance of a sexual signal in a parasitized population of field crickets. Biol. Lett. 2006; 2: 521-524 https://pubmed.ncbi.nlm.nih.gov/17148278/

[3] Pascoal, Cezard, Eik-Nes, Gharbi, Majewska, Payne, Ritchie, Zuk & Bailey. 2014. Rapid Convergent Evolution in Wild Crickets. Current Biology. http://dx.doi.org/10.1016/j.cub.2014.04.053

Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica

El artículo El silencio de los grillos se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Un genio desconocido del Renacimiento
2. El océano en una caracola
3. El sonido del viento (2)

En mi anterior entrada en el Cuaderno de Cultura Científica, A vueltas con el origen del ajedrez, mencionamos la fructífera relación que ha existido, y existe, entre las matemáticas y el ajedrez.

Muchos rompecabezas matemáticos y juegos de ingenio tienen al tablero y las piezas del ajedrez como elementos principales. En esta entrada vamos a prestar atención a algunos problemas que utilizan la pieza del caballo, con su movimiento característico en forma de L, moviéndose en todo el tablero o en parte del mismo. Uno de los principales problemas de este tipo es “el recorrido del caballo en el tablero de ajedrez”, que interesó a grandes matemáticos como Abraham de Moivre, Pierre de Montmort, Leonhard Euler o Adrien-Marie Legendre, y sobre el que podéis leer, por ejemplo, en el libro Del ajedrez a los grafos, la seriedad matemática de los juegos (RBA, 2015). Sin embargo, en esta entrada vamos a interesarnos por el problema de Guarini y otros relacionados.

Monolitos rotados (1988), del matemático británico Ron Brown, pertenece a una serie de obras que toman el problema del recorrido del caballo como herramienta de creación artística. Fotografía de Stephen Barth en el artículo The Use of the Knight’s Tour to Create Abstract Art

El problema de Guarini pertenece a una familia de juegos solitarios que consisten en intercambiar la posición de dos grupos distintos de fichas, normalmente de diferente color, blancas y negras, ya sea mediante el desplazamiento de las mismas –como Todas cambian, La estrella de ocho puntas o el Kono de cinco– o permitiéndose además saltar sobre las fichas contrarias –como El salto de la rana o El puzzle dieciséis inglés (sobre los que se puede leer en el artículo El salto de la rana, y familia), aunque en este caso las fichas son los caballos blancos y negros del ajedrez.

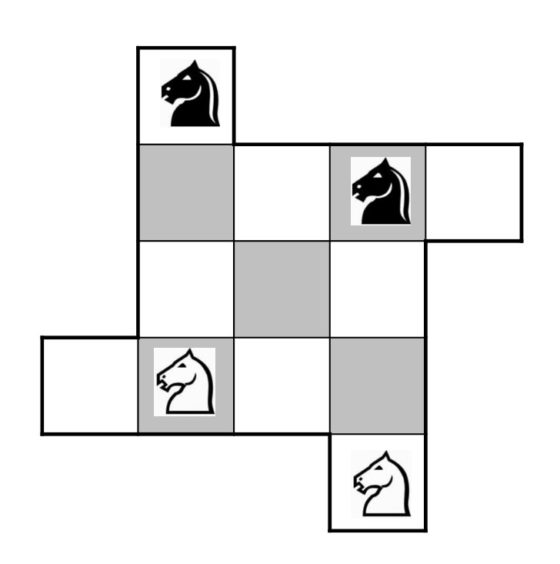
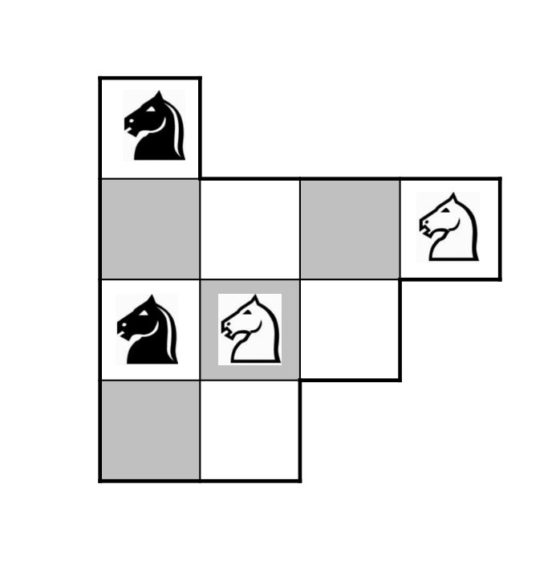
Antes de adentrarnos en el problema de Guarini os propongo jugar a dos versiones de un solitario de esta familia de juegos de intercambio de fichas sobre cierto tablero, el sencillo juego Todas cambian. En ambas versiones se juega con tres fichas (aunque puede generalizarse a un número mayor) de cada color, blancas y negras, sobre los tableros y con las posiciones iniciales que se muestran en la imagen.

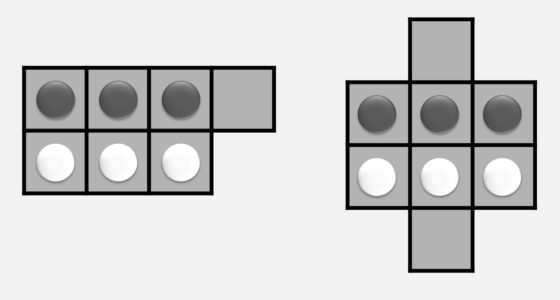
Las reglas del solitario Todas cambian son las siguientes:

i) las fichas se mueven de una en una, y cada una puede desplazarse a una posición adyacente que esté libre;

ii) cada desplazamiento puede ser realizado en horizontal (a izquierda o derecha), en vertical (hacia arriba o abajo) o en diagonal;

iii) el objetivo es intercambiar la posición de las fichas negras y blancas en el menor número de movimientos posible.

Estos son juegos ideales para pasar un buen rato, y su solución es lo que podríamos llamar una demostración constructiva. Sabemos que existe solución al reto porque la encontramos explícitamente, la construimos.

Por otra parte, el procedimiento para encontrar la solución es el básico método del ensayo y error, que consiste en realizar repetidos y variados intentos, en muchas ocasiones sin una regla aparente, hasta alcanzar el éxito. El problema de este procedimiento es que se trata de una búsqueda aleatoria, que no garantiza encontrar la solución, salvo que sea posible explorar todas las opciones, y aunque se encuentre la solución, no genera una técnica útil para utilizar con otros problemas, ni explica el motivo de la misma.

Antes de seguir leyendo, os animo a jugar a estos solitarios y a buscar vuestras soluciones a los mismos.

No es difícil de demostrar que la solución al primer juego puede alcanzarse en siete movimientos. Si numeramos los cuadrados de la primera fila como 1, 2, 3, 4 y de la segunda 5, 6, 7, y describimos cada movimiento como un par de números, la casilla origen de la ficha y la de llegada, entonces, la solución se puede expresar: (7,4), (2,7), (5,2), (1,5), (6,1), (3,6), (4,3). En realidad, no necesitamos tanta información, nos bastará con mencionar cuál es el hueco sin ficha, a partir del 4 inicial, esto es, 7 – 2 – 5 – 1 – 6 – 3 – 4.

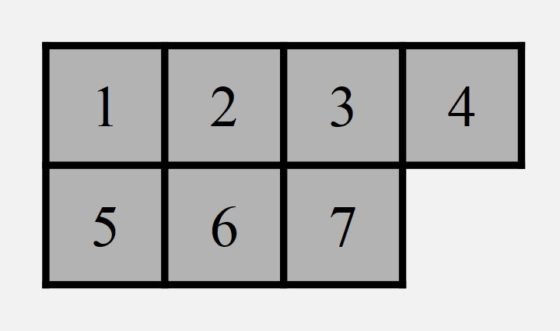
En diez movimientos se pueden intercambiar las fichas en el segundo tablero, aunque si se añade la condición extra de mover las fichas blancas y negras alternativamente, entonces serán necesarios un mínimo de doce. Es aconsejable mantener un registro de los movimientos realizados para comprobar que la solución ha sido correcta y contar el número de pasos.

Fotografía de la exposición Acromática. Una partida inmortal de Mabi Revuelta, en el Azkuna Zentroa, de Bilbao, en la cual el ajedrez, y en particular, la conocida como partida inmortal, es un elemento fundamental de esta exposición de la artista bilbaína Mabi Revuelta

Pero vayamos ya al pasatiempo relacionado con el ajedrez, el problema de Guarini. Este juego nos sirve además para ilustrar un procedimiento muy útil en el trabajo matemático, como es cambiar el punto de vista. Si el problema que estamos intentando resolver es complejo o la técnica que estamos utilizando no parece la apropiada, transformar el problema original en otro más sencillo o para el que conozcamos algún procedimiento que permita resolverlo, puede ser una estrategia exitosa.

El Problema de Guarini, de intercambio de caballos en un tablero de ajedrez de tamaño 3 x 3, aparece como el problema 42 en un manuscrito de 1512 del impresor, tipógrafo y arquitecto italiano Paolo Guarini di Forli (1464-1520), y dice lo siguiente:

“Dos caballos blancos y dos caballos negros están colocados en las cuatro esquinas de un tablero cuadrado de nueve casillas; se pide hacer pasar, según las reglas, los caballos blancos al lugar que ocupan los caballos negros, e inversamente, sin salirse del cuadrado”.

Aunque es algo muy conocido, vamos a recordar primero cómo es el movimiento del caballo en el ajedrez. Esta pieza realiza un salto o movimiento en forma de L –dos casillas hacia delante y una a un lado– como los que se muestran en la siguiente imagen.

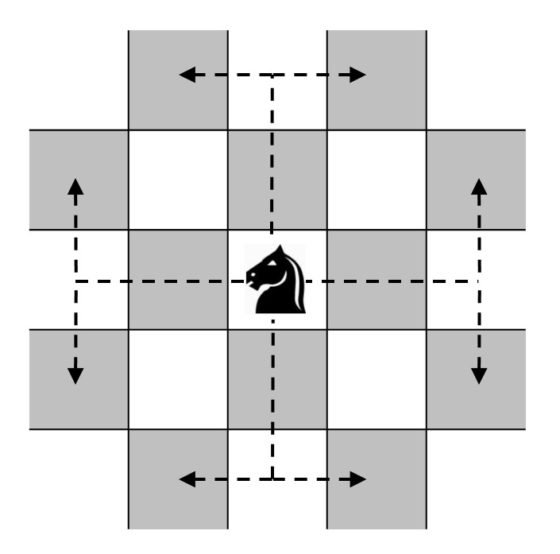
En la siguiente imagen se muestra el tablero del problema de Guarini y su posición inicial.

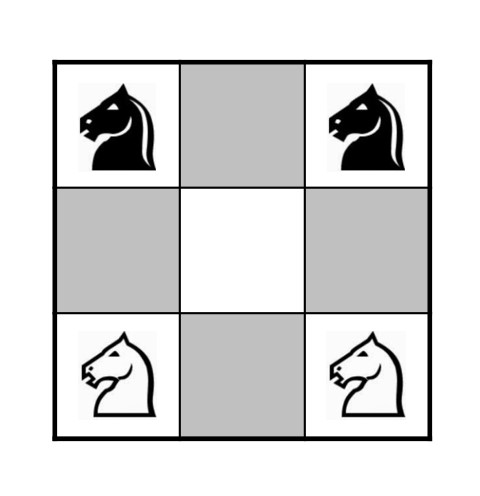
Este solitario ya aparecía en la recopilación de problemas de ajedrez y juegos de tablero del siglo XV, Civis Bononiae (Ciudadano de Bolonia), aunque realmente esa fue solo su primera aparición en Europa, puesto que había sido incluido, unos siglos antes, en el primer manuscrito árabe sobre ajedrez kitab ash-shatranj (hacia el año 840) del jugador y teórico árabe del shatranj, una forma antigua de ajedrez, al-Adli.

Un primer acercamiento al problema de resolver este desafío, consiste en transformarlo en el llamado Juego de la estrella de ocho puntas, que realmente no es más que el grafo asociado al Problema de Guarini.

La idea es representar mediante un esquema sencillo y útil los posibles movimientos del caballo en el tablero de ajedrez 3 x 3. Las casillas del tablero (que numeramos del 1 al 9 como en la imagen de abajo) se van a representar como puntos o círculos y los movimientos del caballo, de una casilla del tablero a otra, se representan mediante líneas que unen esos círculos (salvo el cuadrado central que es un punto aislado).

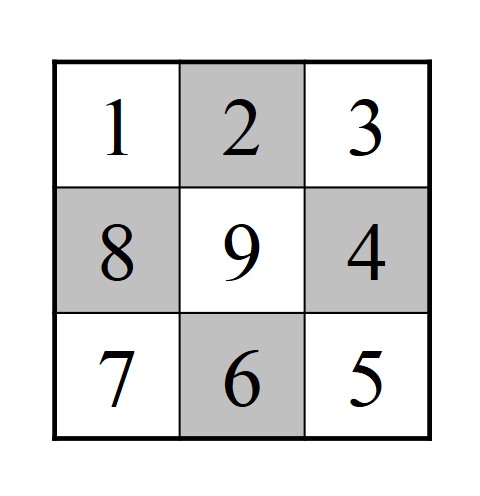
Así, se obtiene una estrella de ocho puntas y el Problema de Guarini de cambio de posición de caballos se transforma en el solitario que consiste en intercambiar la posición de las fichas blancas y negras (que son los dos caballos blancos y los dos negros), siendo los posibles movimientos de las fichas los desplazamientos a lo largo de las líneas de la estrella.

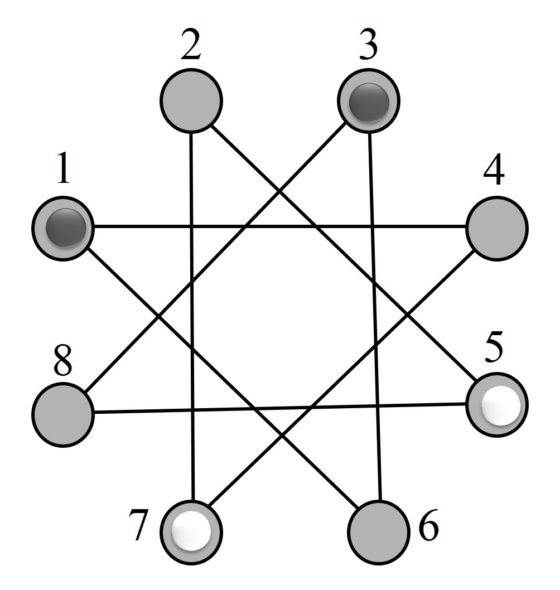
Esta presentación más moderna y sencilla del problema de Guarini, al igual que el problema original sobre el pequeño tablero de ajedrez, puede intentar solucionarse con el habitual método de ensayo y error. Sin embargo, antes de abalanzarnos sobre el mismo, podemos analizarlo un poco más y descubrir que realmente es un problema más simple de lo que aparenta, si se enfoca convenientemente.

Si nos fijamos en las líneas que unen los círculos, observaremos que realmente constituyen un ciclo circular cerrado. Por lo tanto, podemos desenrollar la estrella y transformarla en el circuito circular de la imagen, siendo la solución del solitario tan simple como desplazar las fichas en uno de los sentidos, por ejemplo, en el de las agujas del reloj.

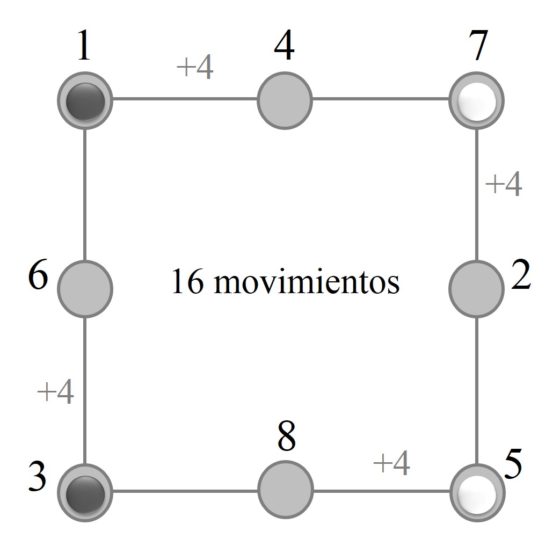
La solución consta de dieciséis movimientos, que consisten en desplazar cada una de las fichas cuatro posiciones en el sentido de las agujas del reloj. Esta solución llevada al problema de Guarini original describe en un cierto movimiento simétrico de los caballos alrededor del cuadrado central. El matemático recreativo británico Henry E. Dudeney (1857-1930) llamaba al anterior método de resolución, el “método de los botones y la cuerda”.

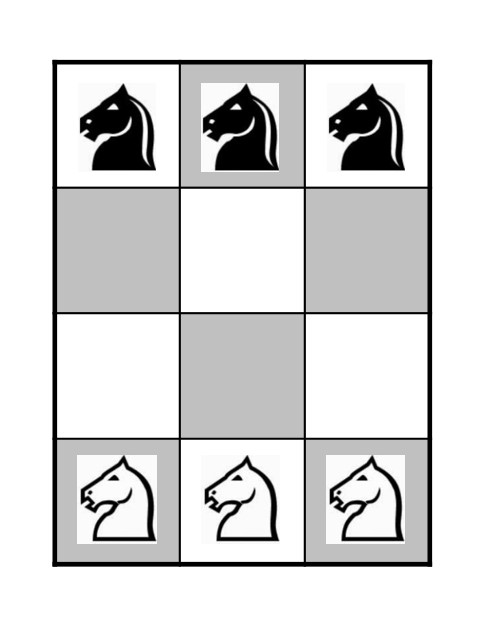
Relacionados con el problema de Guarini se han planteado otros problemas similares en los cuales se cambiaba el tamaño y forma del tablero de juego, y/o el número de caballos. La primera variante de este problema, para un tablero de tamaño 3 x 4, fue publicada en la revista Journal of Recreational Mathematics en 1974 (y posteriormente, en Scientific American en diciembre de 1978). El tablero y la posición inicial de la misma es la siguiente.

El método para resolverlo es de nuevo construir el grafo, de puntos y aristas, asociado al juego. Esta variante del problema de Guarini se transformaría en un problema de intercambio de fichas, tres blancas y tres negras, sobre la siguiente estructura estrellada.

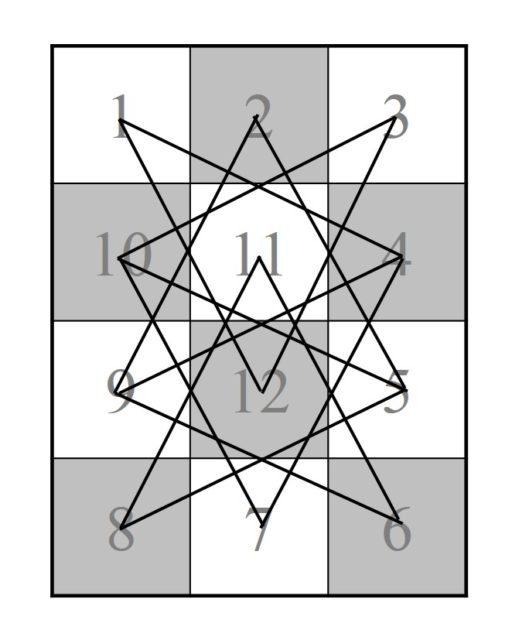
Aunque de nuevo debemos de deshacer el lío de las intersecciones de las aristas y simplificar el grafo, que ahora quedará de la siguiente forma.

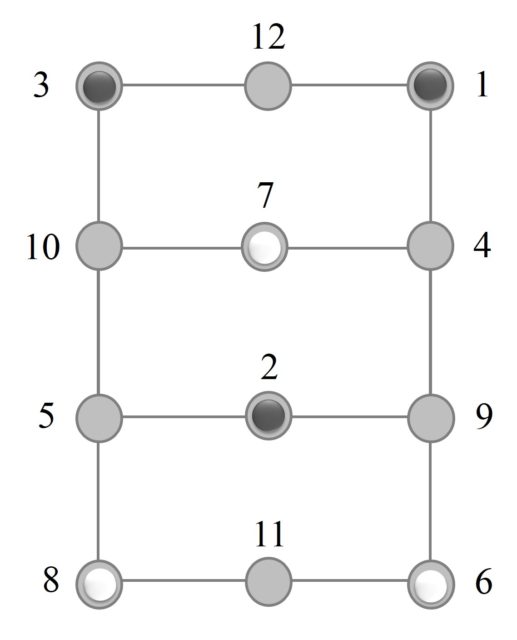
Ahora se pueden intercambiar las fichas blancas y negras en dieciséis movimientos. Para las fichas negras, la ficha de la casilla 1 va a la 6 (3 movimientos), de la 3 a la 7 (2 movimientos) y la de la 2 a la 8 (2 movimientos), en total serían 7 movimientos para las negras. Lo mismo para las blancas, otros 7 movimientos. El problema es que hay cruces entre las fichas blancas y negras, por lo que se necesitan dos movimientos más. En total dieciséis movimientos.

Para terminar con el contenido de esta entrada del Cuaderno de Cultura Científica os dejo planteadas otras dos variantes más.

Las siguientes imágenes, que cierran esta entrada, son dos obras del artista británico Tom Hackney pertenecientes a sus series de obras geométricas que representan partidas de ajedrez del artista y ajedrecista francés Marcel Duchamp (1887-1968).

Chess Painting No. 86 (Devos vs. Duchamp, Folkestone, 1933), del artista Tom Hackney, realizada en 2016. Imagen de la página web de Tom Hackney

 

Chess Painting No. 61 (Duchamp vs. Hanauer, New York, 1952), del artista Tom Hackney, realizada en 2015. Imagen de la página web de Tom Hackney

 

Bibliografía

1.- Raúl Ibáñez, Del ajedrez a los grafos, la seriedad matemática de los juegos, El mundo es matemático, RBA, 2015.

2.- Édouard Lucas, Recreaciones Matemáticas, vol. 1 – 4, Nivola, 2007, 2008.

3.- Miodrag S. Petrovic, Famous Puzzles of Great Mathematicians, AMS, 2009.

4.- Ron Brown, The Use of the Knight’s Tour to Create Abstract, Leonardo, Vol. 25, No. 1, pp. 55 – 58, 1992.

5.- John J. Watkins, Across the board, The Mathematics of Chessboard Problems, Princeton University Press, 2004.

6.- Miodrag S. Petrovic, Mathematics and Chess, 110 Entertaining Problems and Solutions, Dover Publications, 1997.

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

El artículo Ajedrez y matemáticas: el problema de Guarini se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. A vueltas con el origen del ajedrez
2. El problema de Malfatti
3. El problema de las flechas de Mahavira

Los conceptos de estructura atómica y nuclear, esto es, que un átomo consiste en un núcleo rodeado por electrones y que el núcleo está compuesto por protones y neutrones, llevaron a una pregunta aparentemente trivial, pero que resultó ser fundamental: ¿Es la masa de un átomo neutro igual a la suma de las masas de los protones, neutrones y electrones que componen el átomo neutro?

Foto: Casey Horner / Unsplash

Esta pregunta puede responderse con precisión porque se conocen las masas del protón, el neutrón y el electrón, así como las masas de casi todas las especies atómicas. Un estudio de las masas atómicas conocidas ha demostrado que, para cada tipo de átomo, la masa atómica es siempre menor que la suma de las masas de las partículas constituyentes cuando se miden en sus estados libres. El átomo más simple que contiene al menos un protón, un neutrón y un electrón es el deuterio, 21H. En este caso, las masas (en unidades de masa atómica, u) de los constituyentes de un núcleo de deuterio, llamado deuterón, son

Masa en reposo de un protón: 1,007276 u

Masa en reposo de un neutrón: 1,008665 u

Masa en reposo total de las partículas libres: 2,01594 u

Masa en reposo del deuterón 2,01355 u

Diferencia (Δm): 0,00239 u.

Aunque la diferencia en la masa en reposo, Δm, puede parecer pequeña, corresponde a una diferencia de energía significativa, debido al factor c2 en la relación E = mc2, donde c es la velocidad de la luz [1]. La diferencia, Δm, en masa, que se llama defecto de masa, corresponde a una diferencia en la cantidad de energía ΔE antes y después de la formación del núcleo, ΔE = Δmc2.

Por lo tanto, si consideramos la formación de un núcleo de deuterio a partir de la combinación de un protón y un neutrón, se “perderá” en el proceso una cantidad de masa de 0,00239 u. Este defecto de masa significa que una cantidad de energía igual a 2,23 MeV [2] debe irradiarse desde este sistema de partículas que se combinan antes de que se constituyan como un núcleo de deuterio.[3]

La pérdida de energía calculada a partir de la diferencia en la masa en reposo se puede comparar con el resultado de un experimento directo. Cuando el hidrógeno es bombardeado con neutrones, se puede capturar un neutrón en la reacción.

Esta reacción no produce fragmentos de partículas que tengan una gran energía cinética, por lo que el defecto de masa de 0,00239 u del deuterón en comparación con la suma de las masas del átomo de hidrógeno y el neutrón debe estar en el rayo gamma. La energía del rayo gamma se ha podido determinar experimentalmente y se ha encontrado que es de 2,23 MeV, ¡exactamente lo calculado! Esto confirma que al formar un núcleo, los constituyentes emiten energía, generalmente como un rayo gamma, correspondiente a la cantidad de diferencia de masa.

También se ha estudiado la reacción inversa, en la que un deuterón es bombardeado con rayos gamma:

Cuando la energía de los rayos es inferior a 2,23 MeV, esta reacción no tiene lugar. Pero si se utilizan rayos de energía de 2,23 MeV o más, la reacción ocurre; algunos fotones se absorben y se pueden detectar protones y neutrones libres.

En resumen: tras la “captura” de un neutrón por un núcleo de hidrógeno (un protón) para formar un deuterón, la energía se libera en forma de rayo gamma. Esta energía (2,23 MeV) se denomina energía de enlace del deuterón. Se puede considerar como la energía liberada cuando un protón y un neutrón se unen para formar un núcleo. Para obtener la reacción inversa (cuando se bombardea un deuterón con rayos gamma), se debe absorber energía. De aquí que se pueda pensar en la energía de enlace también como la cantidad de energía necesaria para romper el núcleo en las partículas nucleares que lo constituyen.

Notas:

[1] Sobre esta equivalencia puede leerse Equivalencia entre masa y energía, dentro de nuestra serie sobre la relatividad, Teoría de la invariancia.

[2] Un factor de conversión conveniente de masa atómica (expresada en unidades de masa atómica) a energía (expresada en millones de electronvoltios) es 1u = 931 MeV. Por tanto (0,00239 u) · (931 MeV/u) = 2,23 MeV.

[3] Además, también se debe perder un poquito más de energía (13,6 eV), emitida como fotón, cuando un electrón se liga a este núcleo para formar un átomo de deuterio.

 

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

 

El artículo La energía de enlace nuclear se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. El modelo protón-neutrón
2. El problema de la estructura nuclear
3. La hipótesis protón-electrón de la composición nuclear

Manuel Peinado Lorca

Fritz Haber.

La “revolución verde” impulsada por el “padre de la agricultura moderna”, el ingeniero agrónomo norteamericano Norman Ernest Borlaug, premio Nobel de la Paz en 1970, no hubiera sido posible si cuarenta años antes los campos de cultivo no hubieran experimentado otra revolución cuyo promotor fue a la vez criminal de guerra y responsable de la salvación de la agricultura moderna.

Inspire a fondo. Seguramente crea que está llenando sus pulmones de oxígeno. No es así. Casi el 80 % del aire que respiramos es nitrógeno, el elemento más abundante en la atmósfera, que es vital para nuestra existencia, porque, entre otras cosas, es un componente esencial de ácidos nucleicos y aminoácidos.

La vida orgánica, nuestra vida, es pura química reactiva, pero paradójicamente el nitrógeno es inerte, pues no interactúa con otros elementos. Cuando respiramos, el nitrógeno penetra en los pulmones y vuelve a salir de inmediato sin provocar reacción alguna salvo la de servir como agente diluyente del oxígeno en la respiración.

Para que nos resulte útil debe adoptar otras formas más reactivas, como el amoniaco, y son las bacterias las que hacen ese trabajo para nosotros, fijándolo y transformándolo en nitratos para que pueda ser absorbido por las plantas en uno de los ciclos fundamentales para el mantenimiento de la vida.

La falta de nitrógeno asimilable por las plantas parecía una barrera insalvable a comienzos del siglo XX. Hasta que el químico alemán Fritz Haber inventó los fertilizantes artificiales hace poco más de un siglo, la producción agrícola dependía del uso de abonos de origen natural (salitre, guano y estiércol, fundamentalmente), unos recursos próximos al agotamiento por la creciente demanda de alimentos impulsada por el incremento demográfico.

Imagen de la página 88 de Bulbs, plants, and seeds for autumn planting: 1897.
Archive.org

En 1907, Haber fue el primero en extraer nitrógeno directamente del aire. Como cuenta Benjamin Labatut, Haber solucionó la escasez de fertilizantes que amenazaba con desencadenar una hambruna global como no se había visto nunca; de no haber sido por él, cientos de millones de personas que hasta entonces dependían de fertilizantes naturales para abonar sus cultivos podrían haber muerto por falta de alimentos.

En siglos anteriores, la demanda insaciable había llevado a empresas inglesas a viajar hasta Egipto para saquear los campos funerarios de los antiguos faraones en busca del nitrógeno contenido en los huesos de los miles de esclavos inhumados con sus dueños para que continuaran sirviéndolos más allá de la muerte.

Como puede leerse en la imagen adjunta recortada del Morning Post de 1820, los comerciantes británicos, estaban adquiriendo rápidamente todo hueso disponible en Europa continental. La batalla de Leipzig (citada como Leipsic en la noticia), también llamada Batalla de las Naciones tuvo lugar entre el 16 y el 19 de octubre de 1813. Cabe señalar que un quintal de la época eran 100 libras, por lo que el artículo habla de un envío de más de 203 toneladas de osamentas.

Los saqueadores de tumbas ingleses ya habían agotado las reservas de Europa continental; desenterraron más de tres millones de esqueletos, incluyendo las osamentas de cientos de miles de soldados y caballos muertos en las guerras napoleónicas, para enviarlos en barco al puerto de Hull, en el norte de Inglaterra, donde los esqueletos eran molidos en las trituradoras de huesos de Yorkshire para usarlos como fertilizante para la tierra verde y agradable de Inglaterra, un mantillo de los campos de batalla que también produjo dientes para ser reutilizados como dentaduras postizas.).

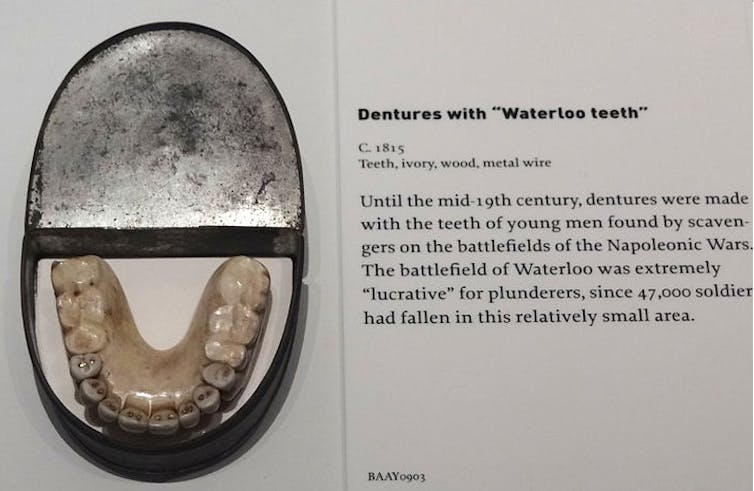Dentaduras postizas con dientes de Waterloo. Museo Militar de Dresde, Alemania.
Adam Jones

Al otro lado del Atlántico, los cráneos de más de treinta millones de bisontes masacrados en las praderas norteamericanas eran recogidos uno a uno por colonos pobres e indios desharrapados para venderlos al Sindicato de Huesos de Dakota del Norte, que los amontonaba hasta formar una pila del tamaño de una iglesia antes de transportarlos a las fábricas de Michigan que los molían para producir fertilizantes.

El saqueo de tumbas cesó cuando Carl Bosch, el ingeniero principal del gigante químico alemán BASF, convirtió en un proceso industrial lo que Haber había logrado en el laboratorio. En poco tiempo, BASF fue capaz de producir cientos de toneladas de nitrógeno en una fábrica operada por más de cincuenta mil trabajadores.

Hombres de pie con un montón de cráneos de bisonte, Michigan Carbon Works, Rougeville MI, 1892.
Colección Histórica Burton, Biblioteca Pública de Detroit.

El proceso Haber-Bosch fue el descubrimiento químico más importante del siglo XX: al duplicar la cantidad de nitrógeno disponible, permitió la explosión demográfica que hizo crecer la población humana de 1,6 a 7 mil millones de personas en menos de cien años. Hoy, cerca del cincuenta por ciento de los átomos de nitrógeno de nuestros cuerpos han sido creados de forma artificial, y más de la mitad de la población mundial depende de alimentos fertilizados gracias al invento de Haber.

En la Gran Guerra (1914-1918), el invento resultó decisivo: después de que la flota inglesa cortara el acceso al salitre chileno, Alemania se habría tenido que rendir mucho antes al no poder alimentar a su población ni obtener la materia prima que necesitaba para seguir fabricando pólvora y explosivos. Los recursos y la potencia industrial eran claves en un nuevo tipo de conflicto bélico, el más global conocido hasta entonces.

Las grandes potencias movilizaron a sus mejores talentos. A principios del siglo XX, la ciencia alemana era puntera; sólo en química, siete de los premios Nobel concedidos entre 1900 y 1918 fueron de esa nacionalidad. Entre estos últimos, Haber fue nombrado responsable del departamento de suministros químicos del ejército alemán.

La Gran Guerra iba ser completamente nueva. En el escenario europeo, las operaciones terminaron estancadas en un frente de trincheras. Las armas que podían ser decisivas, los temibles gases tóxicos, habían sido regulados por los tratados de La Haya que prohibieron utilizarlos dentro de proyectiles de artillería.

Esta prohibición respondía a un dilema ético que había atrapado a políticos, militares y científicos. Apoyado por el sector duro del ejército, Haber, a quien la ética le traía sin cuidado, dio con la solución: los gases estaban prohibidos en los proyectiles, pero ¿y si encontrara una sustancia idónea para liberarla desde bidones y se dejara que el viento hiciera el resto?

El primer ataque con gas de la historia arrasó a las tropas francesas atrincheradas cerca de Ypres, en Bélgica. Al despertar en la madrugada del jueves 22 de abril de 1915, los soldados vieron una enorme nube verdosa que reptaba hacia ellos por la tierra de nadie. A su paso las hojas de los árboles se marchitaban, las aves caían muertas desde el cielo y los prados se teñían de un color metálico enfermizo.

Aprovechando la dirección del viento, los alemanes abrieron unos 5 730 cilindros de cloro, unas 168 toneladas, hacia las filas aliadas durante la segunda batalla de Ypres, en abril de 1915.
Wikimedia Commons

Cuando las primeras patrullas enviadas al silencioso campo de batalla llegaron a las líneas francesas, las trincheras estaban vacías, pero a poca distancia los cuerpos de los soldados franceses yacían por todas partes con las caras y los cuellos arañados intentando volver a respirar. Algunos se habían suicidado. Todos estaban muertos.

Tras el armisticio de 1918 que puso punto final a la Primera Guerra Mundial, Haber fue declarado criminal de guerra por los aliados. Tuvo que refugiarse en Suiza, donde recibió la noticia de que había obtenido el Premio Nobel de Química por un descubrimiento que había hecho poco antes de la guerra, y que en las décadas siguientes alteraría el destino de la especie humana.

El mundo moderno no podría existir sin el hombre que «extrajo pan del aire», según palabras de la prensa de su época, aunque el objetivo inmediato de su milagroso hallazgo no fue alimentar a las masas hambrientas. Con el nitrógeno de Haber, el conflicto europeo se prolongó dos años más, aumentando las bajas de ambos lados en varios millones de personas, cientos de miles de ellos aniquilados por las nieblas letales inventadas por el propio Haber.

Sobre el autor: Manuel Peinado Lorca es catedrático de universidad en el Departamento de Ciencias de la Vida e Investigador del Instituto Franklin de Estudios Norteamericanos, Universidad de Alcalá

Este artículo fue publicado originalmente en The Conversation. Artículo Original.

El artículo El hombre que extrajo pan del aire (pero también mató a millones de personas) se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. El ARN está de moda… desde hace 3 800 millones de años
2. Un fósil neuronal de 25 millones de años: los humanos también orientamos las orejas
3. Las redes 5G no afectan a la salud… pero podrían hacer que el hombre del tiempo acierte menos

Ignacio Peralta Maraver y Enrico L. Rezende

El lagarto de collar (Crotaphytus collaris), muy común en el sur de Estados Unidos y el norte de México. Fuente: Dakota L. / Wikimedia Commons

 

El calentamiento global continua de manera acelerada y sin precedentes. La temperaturas están cambiando tan rápido que muchas especies tienen dificultades para adaptarse, y aquellas que no lo consiguen se extinguen.

Esto es especialmente cierto en el caso de los animales ectotermos, informalmente conocidos como animales de sangre fría, que dependen casi por completo de la temperatura ambiental para regular su metabolismo. Ilustremos el caso con la típica imagen de un lagarto tomando el sol sobre una roca antes de empezar su actividad diaria.

Animales que merman

Una de las consecuencias más llamativas del calentamiento global ha sido la reducción gradual del tamaño en muchos grupos animales alrededor del mundo. Este patrón se ha observado tanto en poblaciones actuales como en el registro fósil.

De hecho, la disminución corporal en animales, junto con los cambios en sus distribuciones y ciclos de vida, se considera ya una respuesta universal del calentamiento global.

Este fenómeno tiene grandes implicaciones en el funcionamiento de los ecosistemas, pero también en el uso que los seres humanos podemos hacer de ellos. Pensemos por ejemplo en la importancia que tiene el tamaño de los organismos marinos para la industria pesquera.

Se han propuesto muchas explicaciones para este fenómeno, pero no se ha contemplado la posibilidad de que las temperaturas puedan afectar de forma diferencial a la mortalidad de los organismos dependiendo de su tamaño.

Muy recientemente, hemos publicado en Nature Climate Change análisis que dan cuenta del impacto del tamaño corporal en la tolerancia al calor. Efectivamente, los organismos pequeños y grandes responden de forma distinta al estrés térmico.

A mayor tamaño, más difícil de calentar

Con la excepción de mamíferos y aves, la mayoría de los animales son ectotermos. Esto supone una enorme diversidad de tamaños y formas corporales, que incluye animales tan pequeños como un mosquito (o incluso menores si consideramos organismos unicelulares) y tan grandes como un cocodrilo africano o un tiburón ballena.

Teniendo esta diversidad de tamaños en mente, nos sorprenderá observar que la gran mayoría de los animales viven en un rango de temperatura muy ajustado: por lo general, entre 0 °C y 40 °C. Entonces, ¿cómo es posible que todos esos animales respondan igual al calentamiento? Pensemos: no cuesta lo mismo calentar un vaso de agua que una bañera de 200 litros.

La respuesta a esta pregunta es que no lo hacen. Pero hasta ahora no se había podido cuantificar, y mucho menos predecir, como varía la tolerancia al calor en función del tamaño.

El tiempo de exposición al calor

Muchos trabajos no pudieron explicar la relación entre el tamaño y la tolerancia al calor por no considerar el tiempo de exposición al que están sometidos los animales.

Un animal podría soportar un calor excesivo por poco tiempo. Pero si el animal está expuesto a este calor (o incluso a una temperatura menor) por un periodo largo, acaba muriendo. Una analogía a este caso la encontramos en los baños de vapor de una sauna. Difícilmente podría aguantar nadie en una sauna durante un día entero.

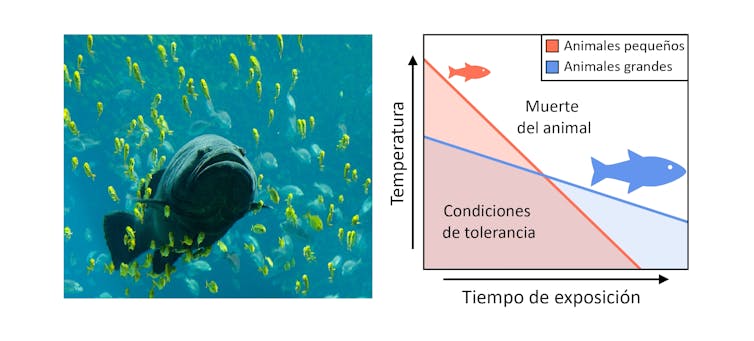La tolerancia al calor depende del tamaño en animales ectotermos (p.e. peces). Animales pequeños resisten temperaturas más elevadas que los animales grandes, pero por cortos periodos de tiempo. Fuente: Los autores

En nuestra ecuación incluimos tanto el calor extremo que pueden soportar los animales como el efecto del tiempo de exposición. Además, ponemos a prueba esta ecuación en artrópodos, moluscos, anélidos, peces, anfibios y reptiles.

El calor no afecta igual a grandes y pequeños

Nuestros resultados muestran que los animales ectotermos de pequeño tamaño aguantan temperaturas más elevadas, así como aumentos repentinos de las mismas. Esto ocurre por ejemplo en las olas de calor.

No obstante, los animales pequeños resisten al calor por poco tiempo, mientras que los grandes aguantan más en condiciones subóptimas.

Combinando nuestra ecuación con cálculos de metabolismo demostramos también que, con el calor, los animales grandes llegan a sus límites metabólicos antes que los pequeños.

El metabolismo es determinante en el desarrollo de los seres vivos. Por lo tanto, nuestro estudio indica que los animales ectotermos de gran tamaño verán más limitado su crecimiento con el calor excesivo.

Nuestro descubrimiento supone una poderosa explicación a la reducción de tamaño como causa del calentamiento global: los ejemplares mas pequeños tendrían una mayor capacidad de resistencia y dejarían mayor descendencia.

Límites de tolerancia al calentamiento global

El calentamiento global no ocurre igual en las diferentes regiones de nuestro planeta. Hay zonas donde el calentamiento es más rápido que en otras. Por ejemplo, las zonas tropicales se están calentando más deprisa que los polos.

Como resultado, algunas poblaciones animales están más cerca de los límites que pueden soportar que otras simplemente por su distribución.

Se han llegado a proponer medidas para calcular los límites de tolerancia de los animales. No obstante, en nuestro trabajo también discutimos que esas medidas estaban muy por encima del valor real.

Cuando incluimos el efecto del tamaño en esos cálculos, vemos que muchos animales están ya prácticamente al límite. Además, las poblaciones de las zonas tropicales son las más vulnerables al calentamiento.

Esta mejora de los cálculos de la vulnerabilidad de los animales al calentamiento global es un gran avance para identificar grupos de máximo riesgo y protegerlos mejor.

 

Sobre los autores: Ignacio Peralta Maraver es investigador postdoctoral en la Universidad de Granada y Enrico L. Rezende es profesor de Ecología y Evolución en la Universidad Católica de Chile

Este artículo fue publicado originalmente en The Conversation. Artículo Original.

El artículo El tamaño sí importa cuando se trata del calentamiento global se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. El calentamiento global y el aceite de oliva
2. El mural de la cantera: arquitectura, ciencia y arte contra el calentamiento global
3. El tamaño importa en organismos, empresas, ciudades y economías

El invierno (1786) de Francisco de Goya (1746-1828). Óleo sobre lienzo. 275 x 293 cm. Fuente: Museo del Prado

La música nos puede ayudar a hablar sobre el clima y el clima afecta a muchos aspectos de nuestras vidas, también al arte y, en especial, la música.

Isabel Moreno es meteoróloga y presentadora del programa de TVE «Aquí la Tierra» y colabora en el programa «Longitud de Onda» de Radio Clásica tratando temas relacionados con el cambio climático en el marco del mundo de la música.



Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus

El artículo Isabel Moreno – Naukas Bilbao 2019: El cielo en clave de Sol se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Francisco Villatoro – Naukas Bilbao 2019: El abrazo de la plata
2. Raúl Ibáñez – Naukas Bilbao 2019: Teorías fantásticas sobre las grafías de los números
3. Carlos Briones – Naukas Bilbao 2019: Luna

La búsqueda y el desarrollo de nuevos materiales para el almacenamiento de la energía es un área clave de nuestra sociedad, puesto que está íntimamente relacionado con el desarrollo tecnológico y la lucha contra el cambio climático. En este sentido, un estudio de la UPV/EHU ha utilizado por primera vez ionogeles —una combinación de polímero y líquido iónico— para baterías de sodio.

Una de las tecnologías de almacenamiento energético predominantes en el mercado son las baterías de litio-ion que se emplean en coches eléctricos y dispositivos electrónicos como los teléfonos móviles y ordenadores portátiles. Las baterías de litio-ion poseen una gran capacidad energética y son fáciles de producir. Sin embargo, las reservas de litio son limitadas, pudiendo llegar a la situación de falta de litio e incremento de su precio.

En este sentido, “este trabajo se ha centrado en las baterías de sodio. El sodio es un elemento que, a pesar de su menor densidad energética frente al litio, se puede emplear para crear baterías con un menor coste, ya que el sodio puede extraerse de muchas fuentes como puede ser el agua marina”, señala Asier Fernández de Añastro Arrieta, investigador del departamento de Química Industrial Aplicada de la UPV/EHU e investigador de POLYMAT.

“El objetivo principal de esta tesis reside en el estudio de nuevos materiales poliméricos para baterías de sodio. Una batería se compone de tres elementos: un cátodo o polo positivo, un ánodo o polo negativo y un material permeable que separa estos dos elementos conocido como electrolito. El electrolito tiene dos funciones principales, una de ellas es la de favorecer la difusión de iones del cátodo al ánodo que hace que podamos cargar o descargar la batería; a mayor y más efectiva difusión de iones, la carga será más rápida y eficiente. La otra función del electrolito en un batería tiene que ver con la seguridad del dispositivo en sí. Es de vital importancia que el electrolito separe físicamente el cátodo y el ánodo y que se mantengan separados durante toda la vida útil de la batería, ya que, el contacto entre el cátodo o el ánodo (por una posible rotura del electrolito) o una fuga del electrolito puede generar un fallo, sobrecalentamiento y en casos extremos, una explosión de la batería de un coche o un teléfono móvil tal y como se ha visto en varias ocasiones en los medios de comunicación”, explica el investigador.

Por ello, “en este trabajo hemos desarrollo membranas poliméricas que actúan como electrolito. Pero no electrolitos poliméricos cualquiera, sino ionogeles. Los ionogeles son materiales que combinan las mejores prestaciones de los polímeros —flexibilidad, bajo coste y ligereza— con las mejores prestaciones de los líquidos iónicos”, cuenta Fernández de Añastro. “Los líquidos iónicos a su vez —continúa—, son líquidos con una gran capacidad de difusión de iones siendo líquidos prácticamente ignífugos. La suma de los polímeros y los líquidos iónicos se materializa en un ionogel, una membrana polimérica, sólida y robusta con una gran capacidad de difundir iones y siendo un material muy seguro debido a su escasa flamabilidad”.

“A lo largo de la investigación hemos sido capaces de sintetizar varios tipos de ionogeles con alto contenido líquido desde un 50 % hasta un 90 %, empleando diferentes métodos físico-químicos con diferentes propiedades. Además, hemos empleado estos materiales en prototipos de baterías reales, como las pilas de botón, y hemos demostrado su capacidad y su buen funcionamiento”, subraya el investigador de la UPV/EHU.

El investigador ha destacado que «el límite que tienen actualmente los líquidos iónicos es su elevado precio; los electrolitos líquidos convencionales que están en todos nuestros móviles son mucho más económicos”. De todas formas, “en los últimos años se ha visto que los líquidos iónicos presentan propiedades excelentes para diversas aplicaciones en la industria. Por lo tanto, por mucho que cuesten si sus aplicaciones lo justifican, quizás podríamos encontrarlos en el mercado en un futuro no lejano”, comenta Asier Fernández de Añastro.

Referencia:

Asier Fdz De Anastro,  Nerea Lago, Carlos Berlanga, Montse Galcerán, Matthias Hilder, Maria Forsyth, David Mecerreyes (2019) Poly(ionic liquid) iongel membranes for all solid-state rechargeable sodium battery Journal of Membrane Science doi: 10.1016/j.memsci.2019.02.074

Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa

El artículo Ionogeles para baterías de sodio se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Las baterías ion sodio, la alternativa estacionaria
2. ADN para la nueva generación de baterías
3. Así funcionan las baterías de litio

Pablo Francescutti

Cibercafé, cibersexo, ciborg, ciberespacio, ciberactivismo, ciberpunk… El prefijo “ciber” se ha vuelto omnipresente, aunque pocos recuerdan que procede de la cibernética, la teoría que a mediados del siglo XX revolucionó las relaciones entre las máquinas y los seres vivos. Este año se cumplen siete décadas de Cibernética y Sociedad, el libro en el que Norbert Wiener propuso una sociedad ideal basada en flujos informativos regulados por ordenadores.

Ya en los años 50 se proponía una sociedad ideal basada en la combinación de la informática con los principios de retroalimentación, autorregulación y flujos informativos, a pesar de que todo lo relacionado con lo «ciber» parezca más moderno. Imagen: Pixabay

Año 1950: la Guerra Fría está al rojo vivo, chinos y americanos se enfrentan en Corea, y la caza de brujas del senador McCarthy envía a miles de artistas y funcionarios al paro o a la cárcel. En ese contexto crispado aparece un libro desbordante de optimismo: El uso humano de seres humanos: Cibernética y sociedad. En sus páginas, Norbert Wiener, un matemático del Instituto Tecnológico de Massachusetts (MIT), proponía una sociedad ideal basada en la combinación de la informática con los principios de retroalimentación, autorregulación y flujos informativos.

No corrían buenos tiempos para la lírica ni para las utopías. El éxito editorial de 1984, la novela de George Orwell publicada dos años antes, reflejaba el estado de ánimo. ¿De dónde sacaba Wiener los recursos intelectuales para contrarrestar al pesimismo distópico? Sencillamente, su propuesta nada tenía que ver con las recetas utópicas habituales, basadas en la reconfiguración integral de las instituciones políticas; en vez de ello se apoyaba en una categoría novedosa: la de información. Esta era a sus ojos la palanca del cambio, la panacea de todos los males sociales.

La información es el elemento fundamental de cualquier sistema biológico o artificial, sostenía Wiener; es más, el ser humano, la sociedad y la naturaleza son información, y es el intercambio de información con el entorno lo que nos permite adaptarnos mutuamente. Para dar cuenta de esa realidad fundó la “ciencia del control de las máquinas y los procesos dinámicos”: la cibernética, término que él mismo derivó del griego kybernetes, que significa timonel o piloto.

El autor de esa visión rompedora había nacido en 1894, hijo de inmigrantes judíos radicados en Massachusetts. “Era un niño prodigio, torpe y obeso”, apunta a SINC Sebastián Dormido, catedrático emérito de informática de la UNED. “A los 18 años se doctoró en filosofía de las matemáticas en Harvard, y tuvo maestros extraordinarios: Bertrand Russell, G. H. Hardy y David Hilbert. Luego se incorporó al MIT”, añade. Miope y bajito, Wiener hablaba ocho idiomas, aunque un chiste decía que no se le entendía en ninguno. Prototipo del sabio distraído, casó con Margaret Engerman (“Fue como criar trillizos”, diría ella de su matrimonio). Un perfil similar en carisma, sentido moral y excentricidad al de la otra celebridad científica de la época, Albert Einstein.

Wiener dando clase en el MIT.

De la artillería antiaérea a la ataxia

La Segunda Guerra Mundial arrancó a Wiener de las matemáticas abstractas: “Quiso desarrollar un cañón antiaéreo guiado por radar que corrigiera automáticamente la puntería, pero no tuvo éxito”, refiere Dormido. Fue un fracaso fecundo, pues orientó su atención a los circuitos de retroalimentación. Por eso, cuando un neurofisiólogo le habló de la ataxia, un trastorno muscular debido a un retraso en la transmisión de señales nerviosas, tuvo una intuición genial: explicarla en función del feed back, la retroalimentación circular que garantiza el equilibrio de un sistema. De allí concluyó “que el cuerpo humano es un sistema de retroalimentación homeostático y que muchos problemas en los seres vivos se deben a fallos de feed back”, apunta el catedrático de la UNED.

“El concepto de feed back no lo inventó Wiener, pero solo él percibió su relevancia en los sistemas biológicos y tecnológicos”, observa a SINC Manuel Armada, especialista en robótica del CSIC. “Supuso que esos mecanismos de control son muy similares en los seres humanos y en las máquinas. En nuestro organismo son ubicuos y se distribuyen horizontalmente, regulando la temperatura o la presión sanguínea”. Su otro gran hallazgo fue ver en la información el idioma universal que permitiría la comunicación entre los seres vivos y las máquinas, al igual que su control (llegó a fantasear con transmitir personas como mensajes. Este escenario de Star Trek era para él teóricamente posible: el reto consistía en diseñar un aparato emisor que tradujera los individuos a datos y un receptor que los reconstruyera a partir de la información recibida).

Su enfoque tendió puentes entre el orden natural y el artificial, granjeándole un enorme prestigio. Pero a Wiener la gloria intelectual no le bastaba. Su espíritu progresista se sublevaba contra los crímenes del fascismo, la división del mundo en bloques irreconciliables y el secretismo impuesto a la investigación por razones militares. Concluyó que el mayor enemigo de la humanidad era la entropía, entendida como pérdida, bloqueo o incomprensión de la información. La guerra favorecía la entropía, al igual que los totalitarismos, pues ambos obstaculizan los flujos informativos.

Portada del libro de Wiener ‘El uso humano de seres humanos: Cibernética y sociedad’

En Cibernética y Sociedad presentó su receta contra la entropía. Imaginó una sociedad descentralizada cuyos dispositivos de feed back la adaptarían automáticamente a las circunstancias cambiantes. Su “sistema nervioso”, los ordenadores, asegurarían que todo funcionase conforme a decisiones racionales. La transparencia resultante del mejor control y tratamiento de la información permitiría una vigilancia social recíproca, que atajaría las conductas negativas. El feliz mundo cibernético se compondría de pequeñas comunidades pacíficas y autogestionadas, y como no habría guerras ni conflictos internos, ni el Estado ni las fuerzas armadas tendrían en él un lugar relevante.

Decantado por el pacifismo, el profesor del MIT se negó a colaborar con la I+D al servicio de la destrucción masiva. Su negativa le convirtió en la personificación de la “ciencia con conciencia”, y se dedicó a alertar a la ciudadanía mediante una serie de ensayos relativos “al mal uso que el poder hace de las máquinas en perjuicio de nuestros congéneres y del planeta”.

El paradigma de moda

En paralelo, la cibernética se irradiaba a los campos más diversos. Haciendo sinergias con la teoría de la información de Claude Shannon, influyó en la biología, la neurociencia y la ecología, entre otros saberes. El politólogo Karl Deustch la aplicó en su modelo de los “nervios del gobierno”; y en el terreno de la salud mental ayudó a ver los trastornos psicológicos como fallos comunicativos en la familia. A los ingenieros les atraía su énfasis en el control de procesos; y a los soviéticos su utilidad de cara a la gestión económica, si bien su aplicación más lograda fue el sistema Cybersyn, que gestionó las empresas nacionalizadas por el gobierno chileno de Salvador Allende.

Al final de su vida, Wiener se horrorizó de los excesos de la automatización. Le espantaban los ordenadores diseñados para lanzar por su cuenta misiles nucleares, a los que calificada de “máquinas ajedrecistas dentro de armaduras”. Anticipando el impacto laboral de las tecnologías de la información, advirtió a los sindicalistas que la introducción de ordenadores en las cadenas de montaje provocaría un desempleo desastroso. Le gustaba comparar a las computadoras que se construyen a sí mismas con el Golem, ese Frankestein de la tradición judía que se vuelve contra su creador. Temía que su teoría “fuera mal utilizada por élites corruptas y egoístas para crear nuevas formas de gobiernos que solo serían eficaces como maquinarias de opresión y manipulación. De modo que se concentró en el desarrollo de miembros prostéticos, que juzgaba más benéficos para la sociedad”, observa Mathew Gladden, experto en Inteligencia Artificial de la Universidad de Georgetown (Estados Unidos). La muerte le sorprendió en 1964 trabajando en un “brazo biónico”.

Una utopía tecnológica

“La palabra cibernética se populariza y luego cae en desuso”, observa Dormido. Efectivamente, en los años siguientes, las aportaciones de Wiener pasaron de moda. Sus sueños de reforma social parecían irrealizables, al igual que su pretensión de fundar un paradigma transversal a todas las ciencias. El protagonismo pasó a desprendimientos de la cibernética como la inteligencia artificial o la teoría de los sistemas autopoiéticos de Maturana y Varela. Pero su núcleo duro, el procesamiento de señales correctoras de errores, “se mantiene vivo en las ingenierías, en los controles de servomecanismos en automóviles, aviones y cohetes, en los sistemas robóticos, en la teoría de la información y la señal, y en el hardware de la telefonía móvil y las redes inalámbricas”, enumera Peter M. Asaro, filósofo de la ciencia de la New School de Nueva York, “aunque ya nadie le llama cibernética”. Y su legado es palpable en la tesis de Donna Haraway de que todos somos organismos cibernéticos (cyborgs), mezclas de materia viva y máquinas unidas por la información.

Su herencia es aún más visible en internet. “La cibernética es el hecho histórico y tecnológico que hizo posible la Red”, declara a SINC Eduardo Grillo, semiólogo de la Academia de Bellas Artes de Nápoles. “La asimilación del pensamiento a los procesos comunicativos entre máquinas, la visión del hombre como el eslabón de una cadena informacional global, el rechazo al secreto y la confianza en que las conexiones posibilitan la auto-regulación de las conductas son ideas de Wiener que inspiraron a la ideología de Internet. Y otro tanto puede decirse de la importancia que atribuía a los canales comunicativos, al poder descentralizador y democratizador de la información y a estar todos conectados, valores que transmitió a los internautas”, apunta Grillo.

Wiener con Torres Quevedo, creador del primer autómata capaz de jugar ajedrez de la historia

 

Pero muchas de sus expectativas se malograron: “Temía que la información se volviese mercancía, contribuyendo a aumentar la ‘entropía social’, y es lo que sucedió. Su esperanza en que la sociedad se autorregulase tampoco se cumplió”, afirma el semiólogo italiano. Igual de frustrantes le hubieran parecido la práctica del secreto y el acceso desigual a la información que caracterizan a nuestra esfera digital, comenta Armand Mattelart, el historiador de la comunicación. “Y si bien su exaltación de la transparencia, las aplicaciones tecnológicas y la conectividad se ha integrado al imaginario de la Red, lo ha hecho subordinada a la lógica de la competencia”, precisa Grillo.

En España el nombre de Wiener es poco conocido, señala Armada, pese a que “nos visitó alguna vez y trató con Leonardo Torres Quevedo a propósito de su ajedrecista automático”. En su país natal su memoria está siendo rescatada del olvido. Creador de una tecnoutopía que se oponía a las tecnologías inhumanas, inventor de máquinas contrario a tratar a las personas como máquinas, es recordado como un profeta. Y aunque su confianza en que la comunicación por sí sola llevaría a la transparencia y al consenso se demostró desmedida, su exhortación a la responsabilidad moral de los científicos e ingenieros tiene más vigencia que nunca, indican sus biógrafos Flo Conway y Jim Siegelman, “La utopía de Wiener era demasiado racional, optimista, ingenua y parcial”, resume Grillo, convencido de “que nos sigue haciendo falta un impulso utópico, ya que las inmensas oportunidades que ofrece la Red dependen también de la idea de sociedad que la inspire”.

Sobre el autor: Pablo Francescutti es sociólogo, profesor e investigador en el Grupo de Estudios Avanzados de Comunicación de la Universidad Rey Juan Carlos (URJC) y miembro del Grupo de Estudios de Semiótica de la Cultura (GESC).

Una versión de este artículo se publicó originalmente en SINC. Artículo original.

El artículo Cibernética utópica: el plan de la sociedad perfecta que sentó las bases de internet se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Científicos y estudiantes se encuentran a través de Internet
2. 1969: el año en el que llegamos a la Luna e inventamos Internet
3. Comunicar la ciencia a la sociedad: el reto de Europa

 

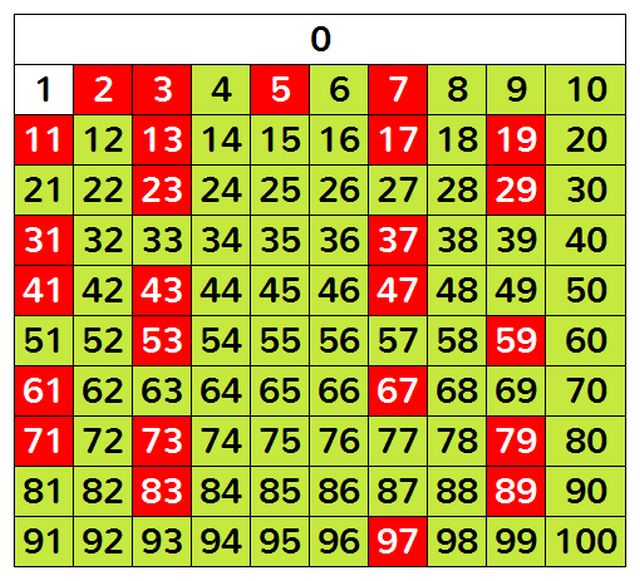Números naturales de cero a cien. Los números primos están marcados en rojo. Imagen: Wikimedia Commons.

 

¿Existe el primo morada de cualquier número entero?

Elije un número entero n mayor que 1. Enumera sus factores primos (con la multiplicidad que corresponda) de menor a mayor y escríbelos concatenados. Al número obtenido aplícale el mismo procedimiento y continúa de este modo. Terminarás cuando obtengas un número primo. Este número primo alcanzado (si existe) se denota por HP(n) y se denomina el primo morada (en inglés, home prime) de n.

Por ejemplo, si n=14, sus factores primos ordenados son (2,7) y obtendríamos el número 27. Sus factores primos son (3,3,3) y conseguiríamos así el número 333. Los factores primos de 333 son (3,3,37), y lograríamos el número 3337. El anterior número factoriza en (47,71), obteniendo al concatenarlos 4771, que es el producto de los primos 13 y 367. Y 13367 es primo, con lo cual habríamos terminado. Así HP(14)=13367. Y, por cierto,

HP(14) = HP(27) = HP(333) = HP(3337) = HP(4771) = H(13367) = 13367.

Observa, además, que si n es un número primo, es HP(n)=n.

Se ha calculado el valor HP(n) para todos los números menores o iguales a 48. Pero aún no se conoce el primo morada (si es que existe) del número 49. Los primeros cálculos no son complicados de realizar:

HP(49) = HP(77) = HP(711) = HP(3379) = HP(31109) = HP(132393) = HP(344131) =…

Como se puede observar, en cada paso las factorizaciones se hacen más complicadas ya que los números intermedios que van apareciendo en este proceso van creciendo.

En agosto de 2016, en la búsqueda de HP(49) se llegó a un número compuesto para factorizar que constaba de 251 dígitos; este número se consiguió tras 118 iteraciones del proceso descrito arriba. Por supuesto, para realizar todos los cálculos involucrados, ha sido necesaria la utilización de recursos computacionales.

El cálculo del primo morada de un número dado se reduce al problema de factorización de números enteros para el cual no existe ningún algoritmo eficiente que lo resuelva.

Además de los problemas computacionales relacionados con la solución de este problema, aún se desconoce si existe el número primo morada de cualquier entero positivo. Aunque se conjetura que sí.

Los detalles de la historia de esta búsqueda se mantienen en el sitio web World of Numbers de Patrick De Geest.

¿Son todos los números afortunados primos?

Multiplica los n primeros números primos. Encuentra el menor entero (mayor que 1) que produce un número primo cuando se añade al anterior producto. Ese número, a(n),se llama un número afortunado (en inglés, Fortunate number, por el antropólogo social Reo Fortune, quien fue el primero es estudiar este tipo de números).

Por ejemplo, si n=6, hacemos el producto:

2 × 3 × 5 × 7 × 11 × 13 = 30030.

El menor entero (mayor que 1) que sumado a 30030 da un número primo es 17. Efectivamente, 30030 + 17 = 30047 es primo y 30030 + m no es primo si m es menor que 17. Así, 17 (= a(6)), es un número afortunado.

Los primeros números afortunados (cada número en la lista, a(n), corresponde al producto de los n primeros números primos) son:

3, 5, 7, 13, 23, 17, 19, 23, 37, 61, 67, 61, 71, 47, 107, 59, 61, 109, 89, 103, 79, 151…

Observar que algunos de ellos se repiten. Además, ¡todos ellos son primos!

De hecho, Reo Fortune conjeturó que a(n) es siempre un número primo. De momento, la conjetura sigue abierta…

Referencias:

Home primes, Futility Closet, 29 diciembre 2020

Home primes (A037274), The OEIS Foundation

Home Prime, Wikipedia

Open Sequences for Home Prime Base 10 (HP10) with n ≤ 11500Fortunate Numbers, Futility Closet, 24 diciembre 2020

Fortunate numbers (A005235), The OEIS Foundation

Fortunate primes in numerical order with duplicates removed (A046066), The OEIS Foundation

Fortunate number, Wikipedia

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad

El artículo Dos conjeturas sobre números primos se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Números primos gemelos, parientes y sexis (2)
2. Buscando lagunas de números no primos
3. Una conjetura sobre ciertos números en el ‘sistema Shadok’

Fuente: CERN

Hasta 1932 el estudio de las reacciones nucleares estuvo limitado por el tipo de proyectil que podía usarse para bombardear los núcleos. Solo las partículas alfa de los nucleidos radiactivos naturalmente podrían provocar estas reacciones. El progreso fue limitado porque las partículas alfa solo se podían obtener en haces de baja intensidad y con energías cinéticas bastante bajas. Estas partículas de energía relativamente baja podrían producir transmutaciones solo en elementos ligeros. Cuando los elementos más pesados se bombardean con partículas alfa, la fuerza eléctrica repulsiva ejercida por la mayor carga del núcleo pesado la partícula alfa, también cargada positivamente, dificulta que la partícula alcance el núcleo. La probabilidad de que se produzca una reacción nuclear se vuelve entonces muy pequeña o nula. Dado que el interés por las reacciones nucleares era grande, la comunidad científica internacional buscó métodos para aumentar la energía de las partículas cargadas para poder usarlas como proyectiles.

Una posibilidad era trabajar con partículas como el protón o el deuterón que tienen una sola carga positiva. Al tener una sola carga, estas partículas experimentarían fuerzas eléctricas repulsivas más pequeñas que las partículas alfa en la vecindad de un núcleo y, por lo tanto, tendrían más éxito a la hora de acercarse lo suficiente como para producir transmutaciones, incluso a núcleos pesados (y por lo tanto de alta carga).

Se podían obtener protones o deuterones a partir de tubos de rayos positivos, pero sus energías eran bastante bajas. Se necesitaba algún dispositivo para acelerar estas partículas a energías más altas, como Rutherford fue uno de los primeros en decir. Estos dispositivos también presentaban otras ventajas: el experimentador podría controlar la velocidad (y la energía) de las partículas bombardeadoras y se podrían obtener rayos de proyectiles muy intensos. De esta forma sería posible encontrar cómo las reacciones nucleares dependen de la energía y naturaleza de las partículas incidentes.

Desde 1930 se han ideado y desarrollado muchos dispositivos para acelerar partículas cargadas. En cada caso, las partículas utilizadas (electrones, protones, deuterones, partículas o iones pesados) son aceleradas por un campo eléctrico. En algunos casos, se utiliza un campo magnético para controlar la trayectoria de las partículas, es decir, para dirigirlas. El tipo más simple tiene un solo paso de alto voltaje de aproximadamente diez millones de voltios, lo que aumenta las energías de electrones o protones a 10 MeV [1].

Otro tipo de acelerador tiene una larga serie de pasos de bajo voltaje aplicados a medida que la partícula viaja en línea recta. Algunas de estas máquinas producen energías de electrones de hasta 20 GeV (1 GeV = 109 eV). Un tercer tipo general utiliza campos magnéticos para mantener las partículas en una trayectoria circular, devolviéndolas una y otra vez a los mismos campos de aceleración de bajo voltaje. La primera máquina de este tipo fue el ciclotrón. Algunos de estos aceleradores producen electrones de 7 GeV o protones de 500 GeV. Gran Colisionador de Hadrones del CERN, produce haces de 6,5 TeV (1 TeV = 1012 eV), y colisiones de 13 TeV. Los aceleradores se han convertido en herramientas básicas para la investigación en física nuclear y de altas energías. Los aceleradores también se utilizan en la producción de isótopos radiactivos y como fuentes de radiación, tanto para fines médicos como industriales.

Estas «máquinas» se encuentran entre las estructuras más complejas y grandiosas jamás construidas. De hecho, son monumentos a la imaginación y el ingenio humanos, la capacidad de razonar y colaborar en grupos, algunos de miles de personas [2], en proyectos pacíficos que fomentan la comprensión de la naturaleza. Básicamente, estas «máquinas» son herramientas para ayudar a la comunidad científica a descubrir la estructura de las partículas nucleares, las fuerzas que las mantienen unidas, la composición última de la materia [3] y, en fin, del universo.

Con el descubrimiento del neutrón en 1932, se creía que solo tres partículas «elementales» eran los componentes básicos de la materia: el protón, el neutrón y el electrón. Pero surgió la necesidad de incorporar otras nuevas, como los neutrinos. A medida que se dispuso de aceleradores de alta energía, se descubrieron partículas «elementales» adicionales, una tras otra. Estas partículas se agrupan en «familias» según sus propiedades. La mayoría de estas partículas existen solo brevemente; la vida útil típica es del orden de 10-8 segundos o menos. Surgió un campo completamente nuevo, la física de altas energías cuyo objeto es discernir el orden y la estructura detrás de la gran cantidad de partículas «elementales» que se han descubierto [4].

Notas:

[1] Para el detalle de la interacción de los campos eléctrico y magnético con las partículas cargadas en movimiento, así como qué unidades se emplean, puede ser interesante consultar Aceleradores y electrón-voltios de nuestra serie Electromagnetismo.

[2] Se estima que en la construcción y operación del Gran Colisionador de Hadrones se ha superado ampliamente la cifra de 10.000 personas de alta cualificación en ciencia e ingeniería implicadas.

[3] Materia en sentido muy amplio del término, lo que incluye ordinaria, oscura y cualquier otra.

[4] Una descripción introductoria a lo que sabemos ahora mismo puede encontrarse en nuestro Del modelo estándar.

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

El artículo La necesidad de los aceleradores de partículas se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. La carga de las partículas radiactivas
2. Las bandas de Bloch
3. Ciencia Express: aceleradores de partículas

Rosa Ballester Añón y Enrique Perdiguero-Gil

Shutterstock / Lucian Coman

 

La utilización masiva de recursos para atajar la pandemia generada por el SARS-CoV-2 puede empeorar otros problemas de salud. Las estrategias en curso para disminuir la mortalidad producida por enfermedades tanto o más mortíferas que la covid-19 pueden quedar en segundo plano. La malaria es uno de los ejemplos. Tanto, que en noviembre de 2020 la Organización Mundial de la Salud pidió que se reforzaran las medidas para luchar contra la enfermedad.

La Estrategia Mundial contra la Malaria 2016-2030 fue aprobada por la Asamblea Mundial de la Salud en 2015. Su audaz objetivo es un mundo sin paludismo. Se pretende que en 2030 se reduzca en un 90 % la carga de mortalidad por esta enfermedad.

Anualmente son diagnosticados más de 200 millones de nuevos casos. El Informe mundial sobre el paludismo 2019 señala que el 93 % de los casos y de las muertes se produce en el África subsahariana. Más de la mitad se diagnosticaron en Nigeria, República Democrática del Congo, Uganda, Costa de Marfil, Mozambique y Níger. Más de dos tercios de los fallecimientos, unos 400 000 en 2018, correspondieron a niños menores de cinco años. Desde 2000 se han reducido significativamente casos y defunciones, pero en años recientes se ha estancado el declive. El paludismo avanza en algunos países, sobre todo en Latinoamérica.

Hace cien años, la malaria tenía carácter endémico en una amplísima franja que incluía Europa y América del Norte. En estas zonas hoy solo aparecen unos pocos casos importados. En España la enfermedad, conocida desde la Antigüedad, se declaró erradicada en 1963.

La malaria (del italiano medieval «mal aire») o paludismo (de paludis, genitivo del término latino palus: ciénaga o pantano) es una enfermedad producida por parásitos del género Plasmodium. Durante siglos, la causa de las fiebres típicas de la enfermedad se atribuyó a determinadas condiciones que creaban un “ambiente palúdico”.

Alphonse Laveran identificó el agente causal de la malaria en 1880. Entre 1891 y 1892 se describieron las diferentes especies del parásito. El papel de las distintas especies del mosquito Anopheles como vehículo de transmisión fue aclarado por Ross y Masson entre 1897 y 1899. Hacia 1902 fue posible plantear estrategias de intervención. Las campañas antipalúdicas incluyeron acciones contra las larvas de los mosquitos, mosquiteras, aislamiento de viviendas y la utilización preventiva de la quinina.

Llegaron las cloroquinas, pero la malaria no se fue

El uso posterior de otras medidas preventivas, como el insecticida DDT, generó cierto optimismo en la lucha contra la enfermedad. Un paso más fue la aparición de la cloroquina, un medicamento de síntesis que permitió superar la escasez de quinina. Se trataba de un optimismo extendido a todas las enfermedades infecciosas En las ediciones de los años sesenta del manual Historia Natural de la enfermedades infecciosas de Burnet y Davis se afirmaba: “En muchos aspectos se puede decir que la primera mitad del siglo XX marca el final de una de las mas importantes revoluciones sociales de la historia: la virtual eliminación de las enfermedades infecciosas como un factor significativo de la vida social”.

La malaria, sin embargo, no desapareció del planeta. Los intentos de globalizar las medidas antipalúdicas desarrolladas por la Sociedad de Higiene de la Liga de Naciones y, más tarde, de la Organización Mundial de la Salud, no tuvieron el éxito esperado. Se utilizaron estrategias de tipo vertical. Fue el caso del uso del DDT y de la cloroquina en la Segunda Guerra Mundial. La enfermedad se había convertido en un problema para los ejércitos aliados. Se decía que era más peligroso que las balas enemigas.

Las actuaciones integrales fueron menos utilizadas. Su objetivo eran los cambios estructurales y las mejoras en las condiciones de vida de las poblaciones. Además debían fortalecerse los sistemas de salud pública. Décadas después, el paludismo continúa siendo un grave problema a nivel mundial.

La búsqueda de una vacuna eficaz y segura es muy reciente. La vacuna RTS,S/AS01 (RTS,S) es la primera y, hasta la fecha, la única efectiva. Permite reducir significativamente la incidencia de la enfermedad y la potencial letalidad para los niños africanos.

La covid-19 y su impacto sobre la malaria

El Día Mundial del Paludismo (25 de abril) de 2019 se inició la primera campaña universal de vacunación infantil contra el paludismo. Según Pedro Alonso, director del programa de malaria de la Organización Mundial de la Salud: “esta vacuna no será la solución definitiva, pero tiene el potencial de salvar miles de vidas y, por ende, contribuirá al desarrollo económico y social de algunas de las zonas más desfavorecidas del planeta”.

En la situación actual, con el trasfondo de la pandemia, algunos autores han hecho estimaciones muy preocupantes. En 2020, en el peor de los escenarios posibles, las muertes por paludismo en el África subsahariana serían unas 769 000. Supondría volver a las tasas de mortalidad de principios de siglo. La causa sería la suspensión de las campañas de distribución de mosquiteros tratados con insecticidas y la reducción del acceso a antipalúdicos eficaces.

Las esperanzas generadas por la vacuna contra la covid-19 no deben oscurecer otras enfermedades infecciosas cuya erradicación es, hoy por hoy, imposible. El fracaso frente al paludismo puede ser una buena vacuna para el virus del optimismo exagerado.

Sobre los autores: Rosa Ballester Añón es catedrática emérita de Historia de la Ciencia y Enrique Perdiguero-Gil es catedrático de Historia de la Ciencia, ambos en la Universidad Miguel Hernández

Este artículo fue publicado originalmente en The Conversation. Artículo riginal.

El artículo Entre incertidumbres y éxitos: la lucha contra la malaria en los últimos cien años se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Historias de la malaria: La lucha contra la malaria
2. Si no puedes con tu enemigo, modifícalo para que te ayude en la lucha contra enfermedades infecciosas
3. Historias de la malaria: La guerra y la historia

Foto: Rohan Makhecha / Unsplash

A finales de 2016 este curioso observador del mundo que acude ante sus lectores cada dos semanas dejaba el año con pesar y pesimismo. Había sido un año pródigo en descubrimientos, con el hallazgo de las ondas gravitacionales como hito máximo. Pero había sido también el de las victorias de Donald Trump en los EEUU y del Brexit en el Reino Unido, en otras palabras, el año de los “hechos alternativos” y la posverdad. El futuro de la ciencia, entonces, se mostraba sombrío.

Durante 2020, la covid-19 ha acaparado toda la atención, pero el año ha dado, en el plano científico, más de sí. Es más, ha sido particularmente fecundo en hallazgos. Veamos, a meros efectos ilustrativos, algunos de los dados a conocer solo en el mes de diciembre.

En astronomía, están reescribiendo la historia de nuestra galaxia. La sonda japonesa Hayabusa2 ha podido traer a la Tierra una muestra de polvo del asteroide Ryugu. Y China ha descubierto casi 19.000 nuevos cráteres en la Luna.

La inteligencia artificial ha producido resultados espectaculares. El algoritmo Alpha Fold 2, predice con éxito la forma de las proteínas a partir de su secuencia de aminoácidos. Y más recientemente, han conseguido resolver la ecuación de Schrödinger, toda una revolución en química cuántica, por las posibilidades que abre para predecir las propiedades de las moléculas a partir de la disposición en el espacio de sus átomos.

En biología estructural y molecular, el último día de 2020 se publicó un método que secuencia el genoma y visualiza su estructura espacial en muestras biológicas intactas.

En neurociencia, se ha conseguido manipular la mente de personas y crear sueños mediante estimulación encefálica no invasiva, lo que abre posibilidades, hasta hace poco inimaginables, de penetrar en los secretos de la mente.

En ciencias ambientales, se ha observado que la disminución de la biodiversidad de ranas en zonas de América Central da lugar a peores brotes de malaria. El hallazgo pone de relieve la íntima relación existente entre la salud humana y la de los ecosistemas. También hemos aprendido que para predecir el comportamiento de los huracanes hay que tener en consideración el efecto de la contaminación atmosférica.

De un orden muy diferente es la autorización para consumo humano, por parte de Singapur, del primer producto cárnico cultivado en el laboratorio (carne artificial). Es el primer paso hacia una gran transformación en la forma de producir y consumir carne para reducir las emisiones de la industria y acabar con el sufrimiento animal.

Esos hallazgos son importantísimos, por sí mismos y por lo que implican. Pero todos empalidecen al lado del diseño y producción de las vacunas de la covid-19, una empresa que podemos considerar quizás como la mayor proeza científica de la historia. Si se superan los obstáculos y la vacunación progresa a un ritmo razonable, la inmunización de miles de millones de personas constituirá el mayor refrendo posible a la ciencia como instrumento de redención. Esta es la gran noticia de finales de 2020.

Hay más. La salida de Trump de la Casa Blanca es la mejor noticia para la ciencia en los Estados Unidos y también una buena nueva, en este ámbito, para el conjunto de la humanidad. Y la Unión Europea, por fin, ha tomado conciencia de la importancia de actuar al unisón en asuntos de carácter estratégico; cabe esperar que, en adelante, lo haga en investigación científica y tecnológica en mayor grado que hasta ahora.

El desarrollo de las vacunas de la covid-19 de 2020 sería así el punto de partida para una época de más progreso y bienestar, una época de transición hacia otros, mejores, tiempos.

Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU

El artículo Mejores tiempos para la ciencia se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Ciencia Clip: un concurso de vídeos de ciencia para jóvenes estudiantes
2. Ciencia para todos a través del cine y la literatura de ciencia ficción
3. El temor en los tiempos del ébola, por Guillermo Quindós

Catástrofe Ultravioleta #34 OLVIDOS

Despedimos la temporada con algunos de los olvidos históricos en nuestro país. La memoria de Cajal desperdigada por los puestos de un rastro, una casa amarilla pionera en el estudio animal y el proyecto de un carpintero que quiere recuperar del olvido un galeón del siglo XVI.

https://www.ivoox.com/t03e10-8211-olvidos_md_63118363_wp_1.mp3

Puedes escucharnos en:

– Podium Podcast
– iVoox
– Spotify
– Apple Podcasts

Agradecimientos: César Calavera, David Barrós, Juan Andrés de Carlos (Instituto Cajal-CSIC), Santiago Ramón y Cajal Agüeras, Fernando de Castro, Juan Pimentel, Alberto Relancio Menéndez (Fundación Canaria Orotava de Historia de la Ciencia), Ander Izagirre, Xavier Agote (Albaola), Julián Mayorga y su troupe

** Catástrofe Ultravioleta es un proyecto realizado por Javier Peláez (@Irreductible) y Antonio Martínez Ron (@aberron) con el patrocinio parcial de la Cátedra de Cultura Científica de la Universidad del País Vasco y la Fundación Euskampus. La edición, música y ambientación obra de Javi Álvarez y han sido compuestas expresamente para cada capítulo.

El artículo Catástrofe Ultravioleta #34 OLVIDOS se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Catástrofe Ultravioleta #30 INMERSIÓN
2. Catástrofe Ultravioleta #31 SIBERIA
3. Catástrofe Ultravioleta #32 TANATOS 1

Un estudio realizado por investigadores del departamento de Geografía, Prehistoria y Arqueología de la UPV/EHU muestra que las lapas de la especie Patella depressa son un indicador climático de alta resolución con importantes implicaciones para futuros estudios arqueológicos y paleoclimáticos.

Patella depressa Pennant, 1777. Fuente: WoRMS

Los análisis de las relaciones de isótopos estables de oxígeno en conchas de moluscos marinos permiten reconstruir las condiciones oceanográficas del pasado, y relacionarlas con el modo de vida de las poblaciones humanas durante la prehistoria. De manera previa al análisis de las muestras arqueológicas es preciso analizar conchas actuales para determinar si la especie encontrada es un adecuado indicador de las condiciones climáticas durante su crecimiento. A pesar de que la especie Patella depressa es una de las especies más representadas en el registro arqueológico del Holoceno a lo largo de la costa atlántica de Europa esta especie no había sido testada como indicador para la reconstrucción de la temperatura del mar.

Un estudio, codirigido por el investigador de la UPV/EHU Asier García Escárzaga en colaboración con investigadores del Instituto Max Planck y la Universidad de Cantabria, ha demostrado por primera vez que la especie Patella depressa es un adecuado indicador climático. Esta investigación combina un estudio de los patrones de crecimiento de las conchas y un análisis de isótopos estables de oxígeno.

Las temperaturas del mar reconstruidas a partir de los valores isotópicos de las muestras modernas reproducen adecuadamente las variaciones de la temperatura del mar durante la vida de los especímenes analizados. Estos resultados confirman que los análisis de isótopos estables de oxígeno en conchas de la especie Patella depressa son un magnífico indicador de las condiciones climáticas actuales y pasadas.

Esta novedosa investigación tiene, además, importantes implicaciones para el análisis de conchas arqueológicas que permitirá determinar los patrones de explotación del medio marino por parte de las poblaciones humanas durante la prehistoria y el impacto que los diferentes cambios climáticos ocurridos durante el pasado tuvieron para estos grupos.

Referencia:

Asier García-Escárzaga, Igor Gutiérrez-Zugasti, Manuel R. González-Morales, Alvaro Arrizabalaga, Jana Zech, Patrick Roberts (2020) Shell sclerochronology and stable oxygen isotope ratios from the limpet Patella depressa Pennant, 1777: Implications for palaeoclimate reconstruction and archaeology in northern Spain Palaeogeography, Palaeoclimatology, Palaeoecology doi: 10.1016/j.palaeo.2020.110023

Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa

El artículo Las lapas como indicador paleoclimático de alta resolución se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Los pigmentos respiratorios de alta afinidad
2. Cómo criopreservar células madre
3. Cómo conservar mejor los alimentos con una iluminación inteligente

Existe en nuestro universo un planeta lleno de simetrías. El planeta da vueltas alrededor de su eje y lo hace siempre al mismo ritmo: siempre en base a periodos regulares de tiempo. Tiene su propio satélite, además, que en su órbita obstinada repite siempre los mismos movimientos, siempre en periodos regulares de tiempo. No lejos de ellos, brilla una estrella. Planeta y satélite dan vueltas a su alrededor y… ya sabéis cómo continúa esta historia: periodos regulares de tiempo.

Concierto de Año Nuevo. Fuente: Wiener Philarmoniker

Esto, me diréis, no parece demasiado especial. Al fin y al cabo, habitamos un universo que en tiempos de Newton se comparó con el mecanismo de un reloj. Lo singular es que este planeta está habitado. Y una vez al año, siempre que pasa por un punto determinado de su órbita, las criaturas que lo habitan realizan un ritual de lo más extraño. De repente, cientos de ellas empiezan a golpear las palmas de sus manos entre sí, todos a la vez y lo hacen… sí, en base a periodos regulares de tiempo. Es la gran celebración de la conservación del momento angular y del movimiento periódico, también conocida como Concierto de Año Nuevo.

Aunque dar palmadas al ritmo de la música pueda parecer algo trivial, se trata de una tarea enormemente compleja. Para ejecutarla, no basta con escuchar la música y reaccionar a ella. Si queremos dar las palmadas a tempo, debemos detectar los patrones subyacentes en la música y adivinar cuándo viene la siguiente pulsación. Debemos anticiparnos constantemente a lo que suena.

Desde un punto de vista computacional, por ejemplo, este problema no resulta nada sencillo. Cada año, investigadores de todo el mundo se enfrentan a este reto con nuevos y mejorados algoritmos, con el objetivo de automatizar una tarea que, como humanos, nos resulta casi trivial: dada una pieza musical, ¿dónde se sitúa el pulso?, ¿cómo sabemos cuándo “dar la palmada»? No es de extrañar que los orígenes de la investigación en este ámbito hundan sus raíces en la psicología de la música: para detectar el tempo de una grabación debemos comprender, en paralelo, cómo los humanos percibimos eso que llamamos pulso.

El problema se complica especialmente en el caso de la música clásica. Por un lado, la ausencia de una base clara de percusión (como la batería, omnipresente en otros estilos musicales), hace que sea más difícil detectar picos de energía claramente diferenciados en la señal acústica y que ayuden a marcar el ritmo. Por otro lado, es común que en este tipo de música aparezcan patrones más complejos, como cambios de compás o polirritmos que, incluso para personas con cierta formación musical, pueden resultar difíciles de desentrañar. Todo ello se agrava por el hecho de el tempo que sigue un intérprete casi nunca es constante a lo largo de una misma pieza: lo más común es que varíe de manera expresiva mediante accelerandos y ritardandos; pequeñas flexiones de esos “periodos regulares”, que nosotros identificamos sin ningún problema pero que pueden confundir a las máquinas mejor entrenadas.

A día de hoy, existen multitud de algoritmos que intentan abordar este problema con mayor o menor éxito dependiendo del estilo musical. Los que se centran en el análisis de grabaciones reales (hay otros que analizan audios midi, por ejemplo) deben enfrentarse a dos problemas diferenciados. Por un lado, la detección de los ataques musicales (las notas que tocan los instrumentos, vaya) cuyas duraciones definen el ritmo de una pieza. Por otro, la detección de patrones y relaciones jerárquicas existentes en el ritmo que permiten establecer cuál es el pulso regular subyacente. La cuestión es que para interpretar esos patrones y esas relaciones, los humanos contamos con todo un bagaje cultural que nos permite relacionar esa música con el estilo al que pertenece, su carácter, su estructura… sin esas claves, es fácil que los algoritmos detecten patrones que no son estructurales o que no puedan distinguir entre el pulso de una pieza y sus posibles múltiplos o submúltiplos. Dicho de otra manera: cuando nosotros damos palmas al ritmo de la Macarena, casi siempre lo hacemos con un pulso determinado, pero también podríamos hacerlo al doble de velocidad. Es nuestro contexto cultural (incluso nuestro conocimiento de la coreografía de la canción), lo que nos ayuda a lidiar con esa ambigüedad. El ordenador lo tiene mucho más difícil.

Resulta sorprendente que una tarea tan cotidiana, tan intuitiva y fácil para nosotros, siga eludiendo a la inteligencia artificial. El hecho es que, hasta la fecha, ningún robot ha sido capaz de batirnos en el viejo arte de dar palmadas al ritmo de la música. Quizás, si algún día viene Skynet y las máquinas a conquistarnos, podríamos retarles a bailar un tango, o, peor aún, invitarles al Concierto de Año Nuevo. Seguro que les estallaría la cabeza.

Referencias:

Graham Percival and George Tzanetakis (2014). Streamlined Tempo Estimation Based on Autocorrelation and Cross-correlation with Pulses. IEEE/ACM Trans. Audio, Speech and Lang. Proc., 22(12):1765-1776.

Frederic Font and Xavier Serra (2016). Tempo Estimation for Music Loops and a Simple Confidence Measure. In 17th International Society for Music Information Retrieval Conference (ISMIR 2016), New York, 07/08/2016.

Simon Dixon (2001). Automatic Extraction of Tempo and Beat From Expressive Performances, Journal of New Music Research, 30:1, 39-58.

Almudena Martín Castro (2017). El metrónomo de Beethoven. Modelado físico de un misterio histórico. Trabajo Fin de Grado, Universidad Nacional de Educación a Distancia.

Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica

El artículo La extraña capacidad de sincronizarnos se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. La emoción de las escalas musicales
2. Tema y variaciones
3. El arte de la repetición

 

Para celebrar que esta es mi entrada número doscientos en la sección Matemoción del Cuaderno de Cultura Científica, voy a recurrir a un clásico de la divulgación de las matemáticas, la leyenda del origen del ajedrez.

La relación entre ajedrez y matemáticas ha sido siempre muy fructífera. Problemas clásicos como el recorrido del caballo sobre el tablero de ajedrez o el problema de las ocho reinas, entre otros, fueron estudiados por grandes matemáticos como Carl F. Gauss, Leonhard Euler, Abraham de Moivre o Adrien-Marie Legendre. Así mismo, muchos matemáticos recreativos como Lewis Carroll, W. W. Rouse Ball, Henry E. Dudeney, Sam Loyd, Édouard Lucas, Raymond Smullyan o Martin Gardner, se apasionaron con este juego, incluso fueron grandes jugadores, e inventaron interesantes rompecabezas matemáticos y juegos de ingenio sobre el tablero de ajedrez.

Retrato de jugadores de ajedrez (1911), del artista francés Marcel Duchamp (1887-1968)

Realmente, se desconoce cuál es el origen del ajedrez. Sabemos que fue introducido en Europa por los árabes, que lo habían aprendido de los persas, pero a ellos les pudo llegar tanto de la India, como de China. Su origen, tan remoto en el tiempo, ha propiciado que existan muchas leyendas, una de ellas relacionada con las matemáticas.

En esta, se atribuye su invención al brahmán hindú Sissa ben Dahir, que presentó el juego al rey Shirham de la India. Este, en agradecimiento, quiso premiar al brahmán y le pidió que fuese él mismo quien escogiera la recompensa por tan maravillosa invención. El brahmán solicitó que se le pagase en trigo. Un grano de trigo en pago por la primera casilla del tablero de ajedrez, dos granos por la segunda casilla, 4 por la tercera, 8 por la cuarta, … y así sucesivamente, doblando en cada casilla la cantidad de trigo de la casilla anterior. Al monarca le sorprendió la modestia de semejante petición, por lo que dio orden a sus ministros de que le fuera inmediatamente pagada esa cantidad de trigo.

Días más tarde, el rey enfadado al enterarse de que el brahmán aún no había sido pagado, mandó llamar a sus ministros. Estos le informaron de que había un problema… ¡¡El rey no tenía tal cantidad de trigo!!

Fotograma del hermoso trabajo audiovisual de Cristobal Vila titulado Inspirations (2012), que podéis ver en la página web Etérea Estudios, en el que se muestra la idea de los granos de trigo que hay en las primeras casillas del tablero de ajedrez

 

La cuestión es entonces la siguiente:

¿Cuánto trigo había solicitado exactamente el brahmán?

Veámoslo. Serían, en la primera casilla 1, en la segunda el doble 2, en la tercera el doble 22 = 4, es decir, es la suma de las potencias de 2, desde la potencia 0 (2 elevado a 0 es 1) hasta la 63 (hay 64 casillas y hemos empezado por 20), es decir,

1 + 2 + 22 + 23 + … + 263 (granos de trigo).

Como se observa, la suma de una progresión geométrica, de factor de progresión 2. En matemáticas tenemos una sencilla fórmula para calcular esta suma, que nos dice que esta suma es igual a

264 – 1 = 18.446.744.073.709.551.615,

es decir, más de 18 trillones de granos de trigo.

Pero la cuestión es saber si dicha cantidad de trigo es realmente grande o no, y en caso de serlo, cuánto de grande puede ser.

Si tomamos como cierta la estimación de que hay 15 millones de granos de trigo por metro cúbico, la cantidad solicitada por el brahmán equivale aproximadamente a un billón 230 mil millones (1.230.000.000.000) de metros cúbicos. Si tuviésemos que almacenarla en un silo, este podría tener, por ejemplo, uno de los siguientes tamaños:

i) un silo con una base que fuese igual a la superficie de todo el territorio histórico del País Vasco (que incluye las siete provincias o herrialdes, a saber, Bizkaia, Gipuzkoa, Araba y Navarra, en España, y Lapurdi, Zuberoa y la Baja Navarra, en Francia), que es de 20.664 km2, y que tendría ¡¡¡una altura de casi 60 metros!!!;

ii) o un silo que tuviera una base con la superficie de toda la Península Ibérica (580.000 km2) y que tendría una altura de más de 2 metros; en conclusión, un silo enorme.

Mural Cuarteto de Agricultores (2015), pintado sobre un silo, del artista Guido Van Helten, uno de los murales sobre silos de la ruta artística Silo Art Trail de Australia. Imagen de Destino infinito.

Pero sigamos pensando un poco en el trigo que el rey Shirham tenía que entregar al brahmán y preguntémonos:

¿Había alguna posibilidad de que el rey pudiese conseguir tal cantidad de trigo?

Según la base de datos (FAOSTAT) de la FAO, es decir, la Organización de las Naciones Unidas para la Alimentación y la Agricultura, la producción mundial de trigo en 2017 (último año con datos recogidos) fue de 771.718.589 toneladas de trigo. Luego, para poder calcular las toneladas que tenía que pagar el rey Shirham, necesitamos saber cuánto pesa el trigo. Ese dato nos lo da lo que se conoce como peso específico, la cantidad de kilos por hectolitro (0,1 metros cúbicos), del trigo. Aunque existen variaciones (en función de los tipos de trigo y otros factores), podríamos fijar una cantidad aproximada de 800 kilos de trigo por metro cúbico. Por lo tanto, los, más o menos, un billón 230 mil millones (1.230.000.000.000) de metros cúbicos, pesarían del orden de 984 mil millones (984.000.000.000) de toneladas.

Por lo tanto, si la producción de 2017 era de unos 780 millones de toneladas, se necesitarían unos 1.250 años de producción de trigo (del tamaño de la producción de 2017) en todo el mundo para pagar la deuda.

Pero está claro que la producción en aquel tiempo era muchísimo menor. Si tomamos como referencia la producción mundial de trigo en el siglo XIX, que era menor que 100 millones de toneladas, pero en cualquier caso mucho mayor que en la época de la leyenda, se necesitarían, como mínimo, unos 10.000 años con toda la producción mundial para cubrir la demanda de Sissa ben Dahir. Si tenemos en cuenta que el ser humano empezó a cultivar el trigo, más o menos, hacia el 9.500 a.c., y que entonces la producción era mínima, es posible que toda la producción de trigo de la historia no fuese suficiente para pagar el precio de la invención del ajedrez.

Pan (1949), de la artista ucraniana Tatiana Yablonskaya

Sorprendente, ¿no? Pero démosle una vuelta de tuerca más a la historia:

¿Cuánto tiempo tardaría uno de los sirvientes del rey Shirham en contar la deuda de granos de trigo (suponiendo claro que los tuviese y que contase a una velocidad de un grano por segundo)?

El tiempo que se tarda es de nuevo más de 18 trillones de segundos. Teniendo en cuenta que hay 31.557.600 segundos en un año, nuestra cantidad es más de 584 mil millones de años. Los físicos que estudian el origen del universo (el Big Bang) estiman que este se produjo hace 15 mil millones de años y que, según la teoría vigente sobre la evolución del universo, puede que este dure todavía entre 10 y 15 mil millones de años… luego realmente no existe el tiempo para poder contar directamente, una sola persona, esa cantidad de granos de trigo… Bueno, toda la población mundial actual, unos 7.800 millones de personas, tardaríamos del orden de 75 años entre todos.

Juego de damas, de la artista canadiense Liane Abrieu. Imagen de la página web de la artista

Como decíamos al principio de esta entrada, existen muchos problemas matemáticos y juegos de ingenio que tienen como base el ajedrez, ya sea solo el tablero, o también las piezas del juego. Para terminar esta entrada me gustaría recordar unos pocos de estos juegos para que puedan divertirse “jugando” las personas que así lo deseen.

Problema 1: Dado un tablero de ajedrez, 8 x 8, del que eliminamos dos casillas opuestas de las esquinas (por ejemplo, pongamos en ellas dos peones), ¿es posible recubrir este tablero con fichas de dominó (suponiendo que estas fichas tienen el tamaño de dos casillas)?

Este problema es un clásico que aparece en muchos libros de pasatiempos matemáticos. Es interesante como ejemplo de problema que no tiene solución y hay que buscar un razonamiento que explique el motivo por el cual no existe tal solución.

Problema 2: Si se consideran ahora triominós, que son fichas con tres casillas, pero en forma de L. No puede rellenarse el tablero 8 x 8 con estas fichas, puesto que 64 no es divisible por 3. Sin embargo, si eliminamos una casilla del tablero (por ejemplo, poniendo un peón), ¿será posible recubrir este tablero?

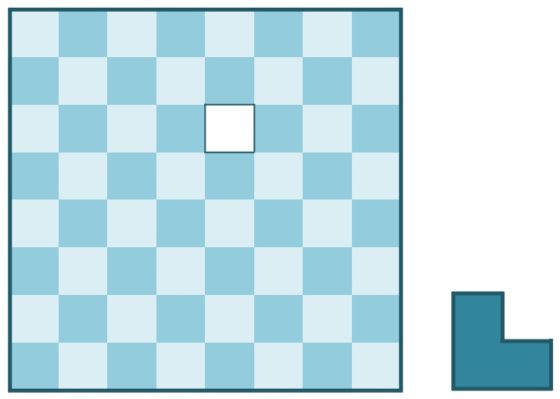
Este es un interesante problema sobre el que podéis leer en la entrada del Cuaderno de Cultura Científica titulada Embaldosando con L-triominós (un ejemplo de demostración por inducción).

Problema 3 (el recorrido del caballo): Utilizando la pieza del caballo, con su particular movimiento en el ajedrez, realizar un recorrido por todas las casillas del tablero, sin repetir casilla.

Este es un problema clásico. Puede leerse sobre el mismo en el libro Del ajedrez a los grafos, la seriedad matemática de los juegos, así como en muchos otros textos. Y otro problema clásico y estudiado por grandes matemáticos es el siguiente.

Problema 4 (las ocho reinas en el tablero de ajedrez): Colocar ocho reinas en el tablero de ajedrez de manera que ninguna de las reinas se vea amenazada por las otras siete.

Puede leerse sobre este problema en el libro Recreaciones Matemáticas, de Édouard Lucas.

Ajedrez 12 (2007) de la artista rusa Agatha Belaya. Imagen de la página web de la artista, donde encontraréis más pinturas relacionadas con el ajedrez

 

El juego del ajedrez (1944), de la artista y escritora estadounidense Dorothea Tanning (1910-2012)

 

Bibliografía

1.- Raúl Ibáñez, Del ajedrez a los grafos, la seriedad matemática de los juegos, El mundo es matemático, RBA, 2015.

2.- Georges Ifrah, Historia universal de las cifras, Ensayo y pensamiento, Espasa, 2002 (quinta edición).

3.- Antonio J. Durán (idea), Vida de los números, textos de Antonio J. Durán, Georges Ifrah, Alberto Manguel, T ediciones, 2006.

4.- Édouard Lucas, Recreaciones Matemáticas, vol. 1 – 4, Nivola, 2007, 2008.

5.- Miodrag S. Petrovic, Famous Puzzles of Great Mathematicians, AMS, 2009.

 

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

El artículo A vueltas con el origen del ajedrez se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. El origen de la escritura de los números
2. El origen poético de los números de Fibonacci
3. ¿Jugar al ajedrez te hace más inteligente? Un vistazo a las pruebas

El filósofo y matemático griego Tales de Mileto creía que la Tierra era un disco flotando en un mar de agua. Para su discípulo Anaximandro la Tierra era un cilindro, con la ecúmene (el mundo habitado) en una de sus tapas planas. Sin embargo, los antiguos griegos terminaron descubriendo que la Tierra tiene forma esférica. Una vez conocida la forma del planeta el siguiente paso fue saber cuál era el tamaño de nuestro planeta y para ello los griegos realizaron algunas estimaciones, utilizando la geometría, del perímetro terrestre. La medición griega más famosa, y certera, del perímetro de la Tierra se debe al polímata griego Eratóstenes de Cirene.  Pero fue el astrónomo persa Al-Biruni quien desarrolló un método más preciso aplicando ecuaciones trigonométricas al ángulo formado entre el pico de una montaña y un plano situado a sus pies. De esa manera calculó que el radio terrestre media 6339.9 km, 17 km menos de lo que en realidad tiene.

Los vídeos de Historias de la Ciencia presentan de forma breve y amena pasajes de la nuestra historia científica y tecnológica. Los vídeos, realizados para la Cátedra de Cultura Científica de la UPV/EHU, se estrenan en el programa de ciencia Órbita Laika (@orbitalaika_tve), los lunes a las 22:00 en la 2 de RTVE.

El artículo Historia del radio terrestre se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. Historia de Nicolas Bourbaki
2. Historia del movimiento ecologista
3. Historia de la tectónica de placas

Durante la toma de esta fotografía de un eclipse total de sol, los neutrinos procedentes del Sol atravesaron la Luna, la cámara, la fotógrafa y el planeta sobre el que esta estaba sin inmutarse. Foto:  karen kayser / Unsplash

La descripción de la desintegración beta en términos de la transformación de un neutrón en el núcleo es parte de una de las historias más fascinantes de la física moderna: la predicción y el eventual descubrimiento de las partículas llamadas neutrino y antineutrino.

Los estudios cuantitativos de las relaciones energéticas en la desintegración beta durante las décadas de 1920 y 1930 plantearon una cuestión difícil y seria. Se idearon métodos para determinar el cambio de energía en un núcleo durante la desintegración beta. Según el principio de conservación de la energía, la energía perdida por el núcleo debe ser igual a la energía transportada por la partícula beta; pero las energías cinéticas medidas de las partículas beta tenían una amplia gama de valores medidos, todos menores que la cantidad de energía perdida por el núcleo. Es decir, parte de la energía perdida por el núcleo parecía haber desaparecido.

Las mediciones realizadas en una gran cantidad de emisores beta indicaron que, en promedio, aproximadamente dos tercios de la energía perdida por los núcleos con desintegración beta parecían desaparecer. Los intentos de encontrar experimentalmente la energía que faltaba fallaron. Por ejemplo, se pensó que esta energía podría ser transportada por rayos gamma; pero estos rayos gamma no se pudieron detectar experimentalmente. El principio de conservación de la energía parecía violarse en la desintegración beta. Se encontraron discrepancias similares en las mediciones del momento del electrón emitido y el núcleo desplazado.

Como en el caso de los experimentos que llevaron al descubrimiento del neutrón, la comunidad física se esforzó mucho en encontrar una alternativa a la posibilidad de aceptar un fracaso de los principios de conservación de la energía y el momento. Estas y otras consideraciones relacionadas llevaron a Wolfgang Pauli a sugerir que otra partícula, que hasta ese momento había pasado inadvertida, se emite en la desintegración beta junto con el electrón, y que esta partícula es la que porta la energía y el momento que faltan.

Esta partícula hipotética no podía tener carga eléctrica, porque la carga positiva del protón y la carga negativa de la partícula beta juntas son iguales a la carga cero del neutrón original. El balance masa-energía en la desintegración del neutrón apuntaba a que la masa en reposo de la partícula de Pauli debería ser muy pequeña, mucho más pequeña que la masa de un electrón y posiblemente incluso cero. La combinación de carga eléctrica cero y masa cero o casi cero haría que la partícula fuera extremadamente difícil de detectar.

Enrico Fermi llamó a esta partícula hipotética neutrino [1]. Fermi construyó un modelo de la desintegración beta basado en la sugerencia de Pauli, en el que un neutrón se desintegra en un protón, un electrón y un neutrino, aquí representado por la letra griega nu (ν):

Este modelo describía adecuadamente los hechos conocidos de la desintegración beta. A partir de 1934, mientras la difícil búsqueda de su verificación experimental aún estaba en curso, el neutrino fue aceptado como una partícula «real» por dos razones, ambas teóricas [2]: salvaba el principio de conservación de la energía en la desintegración, y podía ser utilizado con éxito tanto para describir el resultado de los experimentos de desintegración beta como para predecir los resultados de nuevos experimentos.

Se hicieron muchos intentos infructuosos para detectar neutrinos durante 25 años. Finalmente, en 1956, se detectaron neutrinos en un experimento utilizando el flujo extremadamente grande de neutrinos que sale de un reactor nuclear. La detección de neutrinos es un proceso indirecto que consiste en detectar los productos de una reacción provocada por un neutrino. La reacción utilizada fue una desintegración beta inversa, la producción de un neutrón a partir de un protón. Debido a que el encuentro apropiado de un protón, un electrón y un neutrino en el mismo lugar y al mismo tiempo es un evento extremadamente improbable [3] y el neutrón resultante es difícil de detectar, «atrapar» los neutrinos requerió de una trampa muy elaborada y sensible. Una vez más, la fe en el principio de conservación de la energía se había justificado.

Notas:

[1] En castellano el diminutivo de neutro sería neutrito, en italiano de neutro, neutrino.

[2] En abierta contradicción con los que hablan de “el método científico” como algo único, lo identifican con el método hipotético-deductivo y hacen de la falsación el centro del mismo. La ciencia se basa en actitudes científicas, lo que implica el uso de los métodos que sean menester en cada caso, como este. Véase a este respecto nuestra serie La tesis de Duhem-Quine.

[3] Tanto es así que los neutrinos pueden atravesar toda la Tierra sin alterarse lo más mínimo. De hecho, ahora mismo tu cuerpo está siendo atravesado por neutrinos sin que produzcan efecto alguno.

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

El artículo El neutrino se ha escrito en Cuaderno de Cultura Científica.

Entradas relacionadas:

1. El modelo protón-neutrón
2. La fe en las leyes de conservación
3. Las series de desintegración radiactiva