Divinas matemáticas, ¿matemáticas divinas?
Ojo con el evangelio de hoy
el que habla no sabe
el sabio chino se mantiene en silencio
más de 3 sacudidas es página
2 paralelas que se cortan siempre
constituyen matrimonio perfecto
río que fluye contra su propia corriente
no llegara jamás a feliz término
todo está permitido
libertad absoluta de movimiento
claro que sin salirse de la jaula
2 + 2 no son 4
……………. fueron 4:
hoy no se sabe nada al respecto.
Nicanor Parra, «Ojo con el evangelio de hoy» en «Hojas de parra», 1985
Este hermoso poema de Nicanor Parra (1914-2018) —poeta y “sin embargo” matemático— es una buena manera de introducir este artículo dedicado a cinco conceptos matemáticos con nombres “divinos”.
Comenzamos con arcángeles, con el cuerno de Gabriel (o trompeta de Torricelli), que es una superficie de revolución con volumen finito y superficie infinita.
 El cuerno de Gabriel. Wikimedia Commons.
El cuerno de Gabriel. Wikimedia Commons.
Se obtiene al rotar alrededor del eje de abscisas la hipérbola de ecuación y=1/x, para x ≥ 1. Con una trompeta parecida, según la fe cristina, el arcángel Gabriel anunciaría el juicio final…
El siguiente es un problema de ecuaciones diofánticas —es decir, sus soluciones son números enteros— inspirado en el rebaño del dios griego del Sol. Arquímedes enuncia el problema de los bueyes de Heliosde este modo:
Amigo: Si has heredado la sabiduría, calcula cuidadosamente a cuánto se elevaría la multitud de los bueyes del Sol que, en otro tiempo, pacían en las llanuras de la isla Tinacria distribuidos en cuatro rebaños de colores distintos: uno blanco como la leche, otro berrendo en negro, el tercero colorado y el cuarto jabonero.
En cada rebaño había un número considerable de bueyes repartidos en las proporciones siguientes: el número de los blancos era igual a la mitad aumentada en el tercio de los negros más todos los colorados, mientras que el de negros era igual a la cuarta y quinta partes de los jaboneros más todos los colorados también, y considera, además, que el número de los jaboneros era igual a la sexta y séptima partes de los blancos, aumentado, igualmente, en los colorados.
Las vacas estaban repartidas así: el número de las blancas era, precisamente, igual a la tercera y cuarta partes de todo el rebaño negro, mientras que el de las negras era igual a la cuarta y quinta partes de las jaboneras, todas las cuales habían ido a pacer en compañía de los bueyes, y el número de las jaboneras era igual a la quinta y sexta partes de todo el rebaño colorado, mientras que las coloradas eran en número igual a la mitad de la tercera parte aumentada en la séptima del rebaño blanco.
Amigo: Si me dices exactamente cuántos eran los bueyes del Sol y cuál, en particular, el de bueyes y vacas de cada color, no se te calificará de ignorante ni de inhábil, pero no podrás aún contarte entre los sabios.
Observa ahora los diversos modos de estar dispuestos los bueyes: cuando los blancos juntaban su multitud a los negros, se mantenían en un grupo compacto que tenía la misma medida en profundidad que en anchura, y este cuadrado llenaba completamente las llanuras de Tinacria. Por otra parte, reunidos los colorados y los jaboneros, sin que estuvieran presentes los bueyes de otros colores o sin que faltasen, quedaban agrupados de tal suerte que, constituida la primera fila por uno solo, formaban gradualmente una figura triangular.
Amigo: Si encuentras estas cosas y, en una palabra, si concentrando tu ingenio, expresas todas las medidas de estas multitudes, te glorificarán por haber alcanzado la victoria y se te juzgará como consumado conocedor de esta ciencia.
Este problema fue descubierto en 1773 por el escritor Gotthold Ephraim Lessing, en la biblioteca de Wolfenbüttel en la que trabajaba como bibliotecario. El enunciado, reducido a notación matemática, se resume del siguiente modo: si llamamos W, X, Y y Z a los bueyes blancos, negros, jaboneros y colorados respectivamente, y con las mismas letras pero en minúscula a las vacas del mismo color, tenemos
-
W = (1/2 + 1/3)X + Z,
-
X = (1/4 + 1/5)Y + Z,
-
Y = (1/6 + 1/7)W + Z,
-
w = (1/3 + 1/4)(X + x),
-
x- (1/4 + 1/5)(Y + y),
-
y = (1/5 + 1/6)(Z + z),
-
z = (1/6 + 1/7)(W + w),
-
W + X es un cuadrado perfecto,
-
Y + Z es un número triangular,
-
T = W + X + Y + Z + w + x + y + z.
La solución de este problema, el número T, posee ¡206 545 dígitos!
 Pellegrino Tibaldi: Fresco del Palacio Poggi en el que se representa a los compañeros de Odiseo robando el ganado de Helios. Wikimedia Commons.
Pellegrino Tibaldi: Fresco del Palacio Poggi en el que se representa a los compañeros de Odiseo robando el ganado de Helios. Wikimedia Commons.
Pasamos a los diablos, comenzando por Belfegor, un demonio que seduce a las personas ofreciéndoles inventos ingeniosos que, supuestamente, les proporcionarán riquezas.
 Belfegor. Wikimedia Commons.
Belfegor. Wikimedia Commons.
El número primo de Befegor es:
1000000000000066600000000000001,
un primo palindrómico con el número del diablo 666 situado en el centro.
La escalera del diablo o función de Cantor, posee una cantidad infinita de “escalones”, cada uno de los cuales corresponde a uno de los intervalos eliminados en el proceso de construcción del conjunto de Cantor.
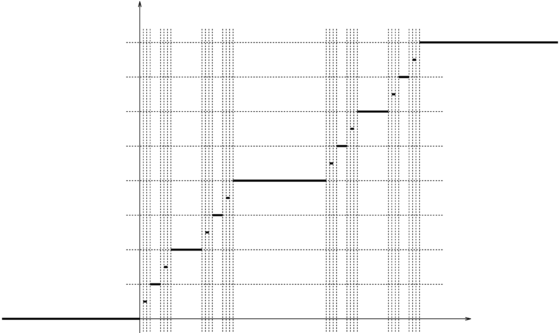 Gráfica de la escalera del diablo. Wikimedia Commons.
Gráfica de la escalera del diablo. Wikimedia Commons.
Abandonamos al diablo para terminar con el número de Dios, el máximo número de movimientos que son necesarios para resolver el cubo de Rubik desde cualquier posición —hay 43.252.003.274.489.856.000 posibles—. Ese número es 20…
 El cubo de Rubik. Wikimedia Commons.
El cubo de Rubik. Wikimedia Commons.
Por cierto, si queréis conocer la superficie de Dios, no olvidéis leer a Alfred Jarry…
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Divinas matemáticas, ¿matemáticas divinas? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- FUN WITH MATHS, diversión con matemáticas
- Más FUN WITH MATHS, diversión con matemáticas
- Ajedrez y matemáticas: el problema de Guarini
Actúa localmente: el dron espía del cambio climático
 Foto: Cameron Venti / Unsplash
Foto: Cameron Venti / UnsplashEl cambio climático afecta a todos los países en todos los continentes, y ya está produciendo un impacto negativo en la economía, la vida de las personas y las comunidades. En un futuro se prevé que las consecuencias serán peores. Si no intervenimos con urgencia las consecuencias en el futuro podrían ser catastróficas.
Hay dos posibles aproximaciones para abordar los problemas derivados del cambio climático: por un lado, reducir las causas del cambio climático tales como la emisión de gases de efecto invernadero (mitigación) y, por otro lado, acomodarse a las nuevas condiciones climáticas con el fin de reducir los daños o beneficiarse de nuevas oportunidades (adaptación).
El precio a pagar por adoptar medidas urgentes que permitan frenar el cambio en el clima puede parecer alto. Sin embargo, no invertir en este tipo de acciones estaría impidiendo adaptarse a las nuevas circunstancias creadas por el cambio climático e incluso generar nuevos puestos de trabajo cuando otros se vean abocados a desaparecer.
El cambio en los patrones climáticos afecta a la temperatura, al nivel y la acidificación del mar, y a la diversidad de las especies. Esto tiene efectos no solo en el mar abierto o en las profundidades marinas, también en las zonas costeras y en la alimentación humana vinculada a la explotación de los recursos marinos.
Por ello se hace necesario ir por delante en la medida de lo posible, desarrollar planes que permitan anticipar y minimizar el efecto del cambio climático sobre los recursos, ecosistemas marinos y áreas urbanas costeras; conservar los hábitats de interés y proteger las especies vulnerables; y gestionar de forma sostenible la pesca y la ordenación del espacio marino.
Para conseguirlo hacen falta datos, muchísimos datos y poder extraer información de ellos. Así, a través de modelos de hábitats y ecosistemas se puede analizar cómo las futuras condiciones climáticas pueden afectar a la distribución, la abundancia y la dinámica poblacional de diferentes especies y grupos tróficos importantes en un ecosistema. Se pueden realizar mapas de riesgo de impactos e indicadores de vulnerabilidad, lo que permite el estudio de posibles medidas correctoras y la elaboración de planes de contingencia.
La cuestión es como obtener datos de manera eficiente. En este caso eficiente implica de una forma mínimamente intrusiva, no contaminante, con un mínimo consumo energético y que esta energía sea renovable, y segura para las personas, todo ello durante largos periodos de tiempo.
AZTI es un centro científico y tecnológico que desarrolla proyectos de transformación de alto impacto relacionados con el medio marino en colaboración con organizaciones alineadas con los ODS 2030 de Naciones Unidas. Junto con Branka Composites, AZTI ha creado el Itsasdrone, un dron de superficie marino para misiones de toma de datos de larga duración y funcionamiento autónomo.

El Itsasdrone funciona solo con energías renovables y cero emisiones. El composite con el que está fabricado contiene un 30% de componentes de origen biológico y los procesos de fabricación son respetuosos con el medio ambiente. Entre las múltiples misiones que puede llevar a cabo están, entre otras, la toma de datos para estudios hidrográficos, muestreos oceanográficos, mediciones de olas y corrientes, análisis de las poblaciones de peces, estudios de migración de especies marinas, mediciones en zonas peligrosas, recopilación de datos meteorológicos y de composición del aire, medición de la actividad solar, monitoreo de derrames de petróleo o detección de desechos marinos.
Pero claro, un dron mínimamente intrusivo con esa capacidad para recopilar datos tiene otras aplicaciones menos, digamos, científicas: desde el control de la industria pesquera o los tráficos ilegales hasta el monitoreo de objetivos militares o la detección de minas. Y el puro y simple espionaje (formalmente, recopilación de datos de inteligencia), claro.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Actúa localmente: el dron espía del cambio climático se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Actúa localmente: tranvías eléctricos sin catenaria
- Actúa localmente: impresión 3D de piezas aeronáuticas de titanio
- Los ecosistemas acuáticos de África y el cambio climático
¿Puede la 5G contribuir a cerrar la brecha digital?
Ana García Armada
 Foto: Frederik Lipfert / Unsplash
Foto: Frederik Lipfert / UnsplashHoy en día no es posible disfrutar de las ventajas de la digitalización en todo el mundo. La Unión Internacional de Telecomunicaciones (UIT), consciente de lo prioritaria que resulta la inclusión digital, tiene un grupo de trabajo dedicado a este asunto.
Hay personas con necesidades específicas (asociadas a diferencias de edad, género, capacidad, nivel socioeconómico y geografía, entre otras) que pueden tener barreras para acceder y utilizar información y servicios digitales, lo que crea una brecha digital (digital divide en terminología anglosajona). Según la UIT, cerca de un 87 % de la población utilizaba internet en países desarrollados en 2019 frente a un 47 % en los países en desarrollo.
Pero no es necesario irnos a países en desarrollo para encontrarnos con ese problema. Como la pandemia ha demostrado, en España hay amplios porcentajes de la población que no tienen el acceso o la capacidad de aprovechar los servicios de banda ancha, y esto sucede por diversos motivos.
La UIT confirma que la población masculina, joven y urbana es usuaria de servicios on line con más probabilidad que las mujeres, habitantes de zonas rurales o población de mayor edad.
Este es un grave problema teniendo en cuenta que la digitalización abre la puerta a oportunidades en áreas como la educación, sanidad, seguridad y crecimiento económico. Como cualquier problema complejo, su solución requiere de acciones combinadas, en este caso en políticas y regulación, educación y tecnología.
Necesidades en política y regulación
Los operadores de telecomunicaciones europeos (agrupados en la European Telecommunications Network Operator’s Association) han publicado un informe sobre cómo el sector puede contribuir a la transformación digital y la recuperación económica. Titulado Conectividad y más: cómo las empresas de telecomunicaciones pueden acelerar un futuro digital para todos, señala que el 83 % de las pymes en la Unión Europea (UE) todavía no usan tecnologías en la nube y el 60 % de los niños y niñas de nueve años se educan en colegios que no están equipados digitalmente.
Estas empresas calculan que la mejora de la infraestructura digital de todas las escuelas europeas requeriría 14 000 millones de euros al año, lo que corresponde al 1,8 % del fondo Next Generation de la UE. Del mismo modo, la digitalización de todas las pymes europeas requeriría 26 000 millones de euros al año, es decir, el 3,5 % del mencionado fondo.
El informe no se queda en un diagnóstico y propone una serie de medidas urgentes tendentes a potenciar la inclusión digital. Entre ellas, incluye el aumento del atractivo que tiene para los operadores invertir en despliegues, facilitar la colaboración a gran escala de las empresas del sector de las telecomunicaciones, estimular la demanda y la transformación digital en sectores industriales y priorizar el liderazgo europeo en servicios digitales y la inversión en habilidades digitales.
Algunas de las novedades de la 5G pueden ayudar en este sentido, bien sea disminuyendo los costes de despliegue y operación, reduciendo el tiempo de despliegue de nuevos servicios, o mejorando el alcance y, por tanto, la cobertura.
La alianza O-RAN
Una de estas novedades tecnológicas de la 5G es la posibilidad de crear redes móviles basadas en software, con gran parte de sus funciones virtualizadas y centralizadas en procesadores de propósito general. Las ventajas de este gran paso en la evolución de la arquitectura de las redes móviles son muchas.
En el contexto de este artículo, cabe destacar que han hecho posible la aparición de un potente movimiento para crear una infraestructura de red abierta, conocido como la alianza O-RAN (Operator Defined Open and Intelligent Radio Access Networks: redes de acceso radio inteligentes y abiertas, definidas por los operadores). Su objetivo es transformar la industria de redes de acceso radio hacia sistemas abiertos, inteligentes y completamente interoperables.
La O-RAN abre la puerta de entrada al mercado a nuevas empresas, diversifica la oferta y redundará, lógicamente, en una mayor competencia y disminución de los costes para los operadores. Dejan de estar atados a un reducido número de fabricantes.
Muestra de la agilidad de este nuevo paradigma es el caso del nuevo operador móvil Rakuten que relata el blog de tecnología de IEEE Communications Society. En septiembre de 2020, tan solo cinco meses después de su lanzamiento inicial, Rakuten Mobile desplegó una red 5G con tecnología en la nube a escala comercial. Debido a la automatización de su red, la compañía asegura que puede proporcionar un nuevo emplazamiento celular 5G en cuatro minutos.
Nuevas frecuencias que facilitan la cobertura
La 5G trae también el uso de nuevas frecuencias en el espectro radioeléctrico. Tal vez las más comentadas sean las bandas de frecuencia muy altas (conocidas como milimétricas), que van a permitir la disponibilidad de grandes anchos de banda.
Sin embargo, no menos importantes son las frecuencias bajas que, a partir de la consecución del segundo dividendo digital, van a permitir alcances superiores a los que teníamos hasta ahora. Esto es así porque las frecuencias más bajas sufren una menor atenuación al propagarse. El potencial de estas frecuencias para cubrir zonas rurales es una oportunidad que no debemos desaprovechar.
Tecnología 5G específica para zonas rurales
Por último, también en relación con la tecnología 5G, hay que mencionar la aprobación en las especificaciones de la Unión Internacional de Telecomunicaciones de una interesante propuesta propugnada por la India.
Los estándares 5G en la UIT se denominan IMT-2020 y recogen una serie de tecnologías que cumplen con los requisitos previamente establecidos (también por la UIT) para avanzar hacia una nueva generación de comunicaciones móviles.
La tecnología de interfaz radio 5G de TSDSI (el organismo estandarizador de la India), denominada 5Gi, fue aprobada por la UIT el 23 de noviembre de 2020. La TDSI destaca en su página web que este estándar es un gran avance para cerrar la brecha digital rural-urbana en la implementación de 5G debido a la mejora de la cobertura. Permite conectar la mayoría de las aldeas de la India de manera rentable. Al ser un estándar mundial, su aplicación no se circunscribe a la India, y ya está encontrando el apoyo de varios países, ya que aborda sus necesidades regionales.
En definitiva, la tecnología nos abre posibilidades que deben concretarse con políticas, formación e información. La 5G, en este sentido, establece una buena base para mejorar la inclusión digital.![]()
Sobre la autora: Ana García Armada, es catedrática de teoría de la señal y comunicaciones en la Universidad Carlos III
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo ¿Puede la 5G contribuir a cerrar la brecha digital? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Puede la 5G interferir con los sistemas de predicción del tiempo meteorológico?
- Naukas Bilbao 2017 – Diana González: Identidad digital y robots
- ¿Puede la física resolver problemas en medicina?
Rana come mosquito
 Foto: Ray Hennessy / Unsplash
Foto: Ray Hennessy / UnsplashEl economista Joakim Weill, de la Universidad de California en Davis, presentó a finales de 2020 en la reunión de la Unión Geofísica Americana una comunicación en la que proponía que brotes de malaria de especial intensidad ocurridos en Costa Rica y Panamá durante las últimas décadas se habían debido a la disminución de las poblaciones de anfibios. Los autores de la investigación, desarrollada por un equipo internacional de procedencias geográficas diversas, habían estudiado un periodo que va de 1976 a 2016. Analizaron el momento y la extensión de los brotes de malaria y, mediante un procedimiento estadístico que valora el posible efecto de varios factores, su posible relación con el declive de los anfibios.
Las poblaciones de anfibios empezaron a declinar en la región a partir de principios de los ochenta, debido a la incidencia de una quitridiomicosis provocada por el hongo Batrachochytrium dendrobatidis. La micosis ha tenido efectos devastadores sobre las poblaciones de anfibios en todo el mundo y a ella se atribuye la desaparición de 90 especies y la reducción de los efectivos de varios centenares más.
El equipo de investigación observó que la incidencia de la malaria en los cantones (Costa Rica) y distritos (Panamá) estudiados se elevó, tras la pérdida de los anfibios, durante tres años hasta alcanzar una meseta que se prolongaba durante cinco años adicionales, para descender a continuación. Se llegaron a producir máximos de incidencia de 1,5 (Costa Rica) y 1,1 (Panamá) casos por cada mil habitantes. De esa incidencia, entre 0,76 y 1 era atribuible al efecto de la disminución de las poblaciones de anfibios. La pérdida de la diversidad de anfibios no fue el único factor que influyó en la incidencia de la malaria –la reducción de arbolado también lo hizo–, pero sí el más importante. La disminución de la incidencia tras los ocho años señalados habría sido consecuencia, probablemente, de las medidas de salud pública implantadas para contener la enfermedad.
La malaria es una enfermedad provocada por protozoos parásitos del género Plasmodium, y es transmitida a los seres humanos por mosquitos del género Anopheles. Se da la afortunada circunstancia de que los anfibios son consumidores de mosquitos, por lo que la reducción de los primeros puede conllevar un aumento de los segundos, si no hay otras especies que sustituyen a los anfibios como depredadores de mosquitos. Por lo tanto, la conexión entre los anfibios y la malaria vendría mediada por la intervención de los mosquitos, como vectores del protozoo.
Recapitulemos: el hongo patógeno mata a los anfibios; menos anfibios comen menos mosquitos, por lo que estos abundan; los mosquitos hembra, que ahora son más numerosos y se alimentan de sangre, pican a más seres humanos y les transmiten el protozoo, de manera que son más los que enferman de malaria. Conviene recordar que la expansión de micosis como la que afecta a los anfibios está provocada, en muchos casos, por actividades humanas, como el tráfico ilegal de animales vivos, o es facilitada por el tráfico internacional de mercancías.
Este es un estudio pionero y es necesario que sus resultados sean avaladas por otros para poder otorgar plena validez a sus conclusiones. Pero el modelo que proponen sus autores resulta verosímil, y no hace sino reforzar la noción de que para garantizar la salud humana es necesario también cuidar la de los ecosistemas y la de sus integrantes. Es la noción “One health” (Una salud), la aproximación a la salud humana y animal que mejor respuesta puede dar a los desafíos que nos plantea el deterioro a que hemos sometido la salud de los sistemas naturales.
Fuente: M. R. Springborn et al (2019): Amphibian Collapses Exacerbated Malaria Outbreaks in Central America. medRxiv
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Rana come mosquito se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Historias de la malaria: El mosquito
- Metamorfosis criogénica de la rana del bosque
- No habrá solución sin más conocimiento
Daniel Marín – Naukas Bilbao 2019: Guía para turistas lunares
 Foto: Andrew Russian / Unsplash
Foto: Andrew Russian / UnsplashTal y como está evolucionando de la cohetería era de esperar que tarde o temprano se necesitase una guía para turistas lunares. Daniel Marín nos la ofreció en primicia.
Daniel Marín es doctor en astrofísica y unas de las referencias en español a nivel mundial en divulgación de la exploración espacial a través de su blog Eureka.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Daniel Marín – Naukas Bilbao 2019: Guía para turistas lunares se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Naukas Bilbao 2017 – Daniel Marín: Algo se muere en el alma cuando una sonda se va
- Nahúm Méndez Chazarra – Naukas Bilbao 2019: Marcianos, extraterrestres y la zona habitable
- Francisco Villatoro – Naukas Bilbao 2019: El abrazo de la plata
Alimentación y sistema inmune
Iñaki Milton Laskibar, Alfredo Martínez Hernández, Irene Besné Eseverri y Maria Puy Portillo
 Foto: Brooke Lark / Unsplash
Foto: Brooke Lark / UnsplashEl sistema inmune es un conjunto de procesos y elementos biológicos que permiten mantener la homeostasis frente a agentes externos. Para ello, cuenta con dos niveles de respuesta inmunitaria. La primera es la no específica o innata, que está formada por barreras físicas, péptidos antimicrobianos y el complemento, entre otros. La segunda es la específica o adaptativa, donde intervienen los linfocitos T y B, así como los anticuerpos.
Para que la función inmunológica de una persona sea adecuada, es necesario cubrir sus necesidades energéticas. Especialmente, cuando el sistema inmune está activado (cuando se producen infecciones, por ejemplo).
Sin embargo, dicho sistema no solo requiere de energía para su funcionamiento, sino también de nutrientes concretos. Por ello, es importante conocer cuáles son estos nutrientes, así como los alimentos que los aportan, a la hora de planificar una alimentación adecuada.
Alimentos amigos del sistema inmune
Como se ha indicado, lo primero será cubrir las necesidades energéticas de la persona. Es fundamental puesto que situaciones de déficit energético (desnutrición) se han relacionado con inmunodeficiencia.
Pero también habrá que evitar ingestas excesivas de energía que pueden derivar en obesidad. Esta se caracteriza por un estado de inflamación crónico, así como por una adiposidad excesiva. Ambas situaciones afectan negativamente a la función inmunológica de una persona, haciéndola más susceptible a infecciones.
En cuanto a los macronutrientes, se considera que tanto los hidratos de carbono simples (azúcares) como los ácidos grasos saturados tienen un efecto proinflamatorio. Por ello, será necesario limitar el consumo de dulces y bebidas azucaradas, así como de carnes rojas, lácteos grasos y productos de bollería industrial (ricos en grasas saturadas).
Por el contrario, el ácido docosahexaenoico (DHA) y el eicosapentaenoico (EPA), ambos de la serie ϖ3, han demostrado tener efectos antiinflamatorios, así como de protección frente a infecciones. Por ello, incluir alimentos como pescado azul y frutos secos en la dieta ayudará a asegurar la ingesta de dichos nutrientes.
Proteinas y fibra
En el caso de las proteínas, se ha observado que cubrir las necesidades de ingesta de una persona favorece la función inmunológica. Se recomienda el consumo de proteínas de alto valor biológico (de alimentos de origen animal y de la soja). Estas juegan un papel fundamental en la producción de anticuerpos. Además, proporcionan aminoácidos con función inmunomoduladora como la arginina y la glutamina.
Por otra parte, asegurar una ingesta de fibra adecuada (entre 25 y 30 g/día) también será fundamental para la inmunocompetencia del sistema inmune debido a su efecto prebiótico. Esto permitirá mantener una microbiota adecuada, la cual favorecerá una función de barrera intestinal correcta. También proporcionará un efecto antiinflamatorio directo (menor producción de citoquinas proinflamatorias) e indirecto (mediante la producción de ácidos grasos de cadena corta, los cuales a su vez tienen un efecto antiinflamatorio).
Por otro lado, se ha propuesto el uso terapéutico de probióticos. Estos han demostrado su efecto antiinflamatorio (como el Lactobacillus rhamnosus y el Bifidobacterium lactis) para el restablecimiento de la respuesta del sistema inmunitario.
El papel de las vitaminas
Al igual que ocurre con los macronutrientes, los minerales y vitaminas también intervienen en el funcionamiento del sistema inmune. Por ejemplo, es bien conocida la importancia que tienen las vitaminas A y D a la hora de protegernos de las infecciones, especialmente las respiratorias.
Para asegurar una ingesta adecuada de estas vitaminas tenemos que incluir en la dieta carnes, pescado y huevos (fuentes de vitaminas A y D), verduras y frutas de colores vivos (fuentes de β–carotenos, precursores de vitamina A) y leche y derivados lácteos grasos (vitamina D).
En el caso de las vitaminas E y C, estas también intervienen en la función inmune. Reducen el estrés oxidativo y evitan la oxidación tanto de ácidos grasos poliinsaturados (como el EPA y DHA) como de células del sistema inmune.
En este caso, los aceites de origen vegetal (especialmente de girasol) y frutos secos aseguran el aporte de vitamina E. Por su parte, las frutas (especialmente cítricos) y verduras son la principal fuente de vitamina C.
Cabe destacar, además, que las frutas y verduras proporcionan polifenoles. Estos son compuestos que ayudan al sistema inmune por sus efectos antioxidantes y antiinflamatorios.
Por último, los déficits de vitaminas B6 (presente en alimentos ricos en proteína), B9 (verduras de hoja verde, legumbres y cereales) y B12 (alimentos de origen animal) se han relacionado con alteraciones en la respuesta inmune humoral y celular, inflamación y menor protección frente a infecciones.
¿Y los minerales?
En cuanto a los minerales, cabe destacar la importancia de todos, pero en especial del zinc (carne roja, legumbres, crustáceos y moluscos), en el sistema inmune. Este último que participa en el mantenimiento de membranas, así como en el crecimiento y diferenciación de las células del sistema inmune.
El hierro (carne, pescado, legumbres y verduras de hoja verde) es otro mineral a tener en cuenta debido a su importancia en el crecimiento y diferenciación de linfocitos T, al igual que el cobre (cereales integrales, frutos secos, legumbres, crustáceos y moluscos) y el selenio (carne roja, pescado, huevo, marisco y cereales integrales). Son necesarios en la proliferación de células T, producción de anticuerpos y la inmunidad celular.
Finalmente cabe destacar que mantener un estilo de vida activo puede ser beneficioso para el sistema inmune. Numerosos estudios han demostrado que la práctica de actividad física no solo tiene un efecto antiinflamatorio, sino que también ayuda a la regulación del sistema inmune y retrasa la pérdida de funcionalidad relacionada con la edad.![]()
Sobre los autores: Iñaki Milton Laskibar, Investigador Postdoctoral en Cardiometabolic Nutrition Group, IMDEA Alimentación. Investigador en Centro de Investigación Biomédica en Red de la Fisiopatología de la Obesidad y Nutrición (CiberObn), UPV/EHU; Alfredo Martínez Hernández, Director de Precision Nutrition and Cardiometabolic Health Research Program y Cardiometabolic Nutrition Group, IMDEA; Irene Besné Eseverri, , Universidad de Navarra, y Maria Puy Portillo, Catedrática de Nutrición. Centro de Investigación Biomédica en Red de la Fisiopatología de la Obesidad y Nutrición (CIBERobn), UPV/EHU
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo Alimentación y sistema inmune se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Día de Darwin 2020: Evolución del Sistema Solar + Teoría evolutiva y medicina
- Saturno tiene el sistema de nieblas en capas más extenso observado en el Sistema Solar
- Modalidades de alimentación
A qué edad perdiste el oído absoluto
 Foto: Lázaro Rodríguez / Unsplash
Foto: Lázaro Rodríguez / UnsplashJenny Saffran se ha pasado años estudiando cómo los bebés aprenden a usar el lenguaje. Es profesora en psicología del desarrollo de la Universidad de Wisconsin-Madison y su trabajo de investigación partió de una cuestión aparentemente sencilla1:
Cuando los bebés escuchan hablar a los adultos, ¿qué es lo que oyen, en realidad?
A fin de cuentas, el habla no es más que una señal sonora más, de entre todas las que nos rodean: variaciones de la presión del aire que empujan suavemente nuestro tímpano varios centenares de veces por segundo. Nosotros, como adultos, percibimos el habla como algo especial: un tejido de letras y sílabas que se agrupan en palabras. En el papel (o en la pantalla sobre la que ahora me lees), esas palabras están claramente separadas mediante espacios y cada una apunta a un significado que podemos definir. Pero en el aire que sostiene nuestras conversaciones, las palabras forman un río continuo de frecuencias y timbres, que un bebé debe aprender a descomponer. Y no es un problema sencillo, en absoluto.
Imagina que escuchases a un alienígena hablando en una lengua desconocida y tuvieses que ir desmigando su discurso en busca de unidades mínimas de significado que os permitan empezar a entenderos. Los miembros más jóvenes de nuestra especie se enfrentan a ese reto cada día y, para resolverlo, utilizan varias claves distintas. Una de ellas, es la prosodia: las melodías y los ritmos del habla, esa música insospechada que todos producimos cada vez que abrimos la boca contiene información clave sobre la estructura del lenguaje (cómo se organiza en sílabas, palabras y frases)2. Pero además, resulta que los bebés son unos expertos en detectar patrones, unas verdaderas máquinas de aprendizaje estadístico. Cada vez que escuchan las vocalizaciones de los adultos, ellos son capacidades de detectar las regularidades que se producen en la señal sonora, qué timbres se repiten en el mismo orden y en qué contextos.
Saffran estudió esta sorprendente habilidad midiendo la atención que prestaban un grupo de bebés de ocho meses a las posibles “palabras” de un idioma inventado3. Durante apenas dos minutos, les hizo escuchar una secuencia de sílabas sin ningún significado aparente (como por ejemplo bidakupadotigolabubidaku). La cuestión es que, dentro de esta secuencia aparentemente caprichosa había algunos grupos de sílabas, “palabras” artificiales, que se repetían en el mismo orden con más frecuencia (como, por ejemplo, bidaku). Cuando, en un segundo test, los bebés escucharon estas mismas palabras inventadas reaccionaron como si ya estuvieran familiarizados con ellas. Les prestaron menos atención que a otros grupos de sílabas, que no habían sido incluidos en un orden determinado durante la secuencia del entrenamiento. Es decir, los bebés habían sido capaces de identificar aquellos patrones de sonidos más repetitivos ¡con apenas dos minutos de entrenamiento!
En un experimento posterior, Saffran quiso comprobar si este asombroso poder de inferencia estadística infantil afectaba al tono de los sonidos y no solo a los fonemas del idioma4. Para ello diseñó un experimento en el que se evaluaba la capacidad de los bebés para reconocer grupos de tonos repetidos. La idea era la misma que en el experimento anterior, pero sustituyendo las sílabas por notas musicales. Si los bebés eran capaces de reconocer aquellos motivos melódicos (las “palabras de notas”) que se repetían con mayor frecuencia dentro de una secuencia continua más larga, no tardarían en habituarse a ellos.
Fue esto, precisamente, lo que sucedió. Cuando los bebés volvían a escuchar los grupos de notas (o motivos) más repetidos durante el entrenamiento, se mostraban menos sorprendidos que cuando estas mismas notas sonaban en un orden nuevo. Pero además, los resultados desvelaban un interesante matiz: para que ese aprendizaje fuese posible, los motivos melódicos debían repetirse exactamente en el mismo tono. Es decir: los bebés de ocho meses no tenían oído relativo, no podían reconocer un mismo contorno melódico cantado a distintas alturas. En cambio, ¡estaban usando su oído absoluto para reconocer las secuencias de notas del experimento de Saffran!
Si el oído absoluto es una habilidad innata que los niños de ocho meses comparten con los pájaros y con el mismísimo Mozart, la cuestión interesante “no es por qué algunas personas lo poseen” como apunta Diana Deutsch5, “sino por qué no es una característica universal”. Según Saffran y su colga Gregory Griepentrog, durante la etapa de adquisición del lenguaje, la mayoría de nosotros lo perdemos en favor de nuestro oído relativo, una habilidad más sofisticada que nos permite generalizar la información tonal del lenguaje e identificar contornos melódicos (prosódicos) aunque no se produzca exactamente a la misma altura ni los entone la misma voz.
Esto explicaría por qué el oído absoluto es más frecuente entre adultos que han recibido un entrenamiento musical temprano, como Mozart y muchos compositores célebres. Su formación habría impedido que “olvidasen” el sentido absoluto de los tonos con el que nacieron. También daría sentido a una curiosa estadística. Casi todos los “savants” con habilidades musicales tienen oído absoluto, y es una habilidad inusualmente frecuente entre aquellos que sufren autismo. Según Leon Miller6, los problemas del habla que a menudo acompañan a estas afecciones podrían haber facilitado que se preservase su oído absoluto.
Referencias:
1Mithen, Steven. “chapter 6 Talking and Singing to Baby Brain Maturation, Language Learning and Perfect Pitch.” The Singing Neanderthals, Harvard University Press, 2007.
2Saffran, Jenny R., et al. “Word Segmentation: The Role of Distributional Cues.” Journal Of Memory And Language, vol. 35, 1996, pp. 606–621.
3Saffran, Jenny R., et al. “Statistical Learning by 8-Month-Old Infants.” Science, vol. 274, 1996, pp. 1926-1928
4Saffran, Jenny R., and Gregory J. Griepentrog. “Absolute pitch in infant auditory learning: Evidence for developmental reorganization.” Developmental Psychology, vol. 37, no. (1), 2001, pp. 74–85
5Deutsch, Diana, et al. “Absolute Pitch, Speech, and Tone Language: Some Experiments and a Proposed Framework.” Music Perception, vol. 21, no. 3, 2004, pp. 339–35.
6Steven Mithen (2007) cita a Miller, L. K. 1989. Musical Savants: Exceptional Skill in the Mentally Retarded. Hillsdale, NJ: Lawrence Erlbaum.
Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica
El artículo A qué edad perdiste el oído absoluto se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:El misterioso número 22
La entrada de hoy quiero dedicarla a una curiosa propiedad relacionada con el número 22. Este es un sencillo número de dos dígitos, que es par, capicúa y semi-primo, es decir, producto de dos primos, ya que es igual al producto de 2 y 11. Además, es un número pentagonal, como vimos en la entrada El asesinato de Pitágoras, historia y matemáticas (y II), un número heptagonal centrado (véase la entrada El problema de las flechas de Mahavira ) y el número de particiones del 8 (recordemos que una partición de un número entero positivo es una forma de expresarlo como suma de números enteros positivos, donde el orden no es relevante; por ejemplo, las particiones del número 3 son tres, a saber {1 + 1 + 1, 2 + 1, 3}, mientras que existen cinco particiones del número 4 {1 + 1 + 1 + 1, 2 + 1 + 1, 2 + 2, 3 + 1, 4}).
 El número atómico del titanio es 22. Imagen de Titanium Mithril
El número atómico del titanio es 22. Imagen de Titanium Mithril
Pero vayamos con la curiosa propiedad del número protagonista de esta entrada, el número 22. Seguid mis instrucciones:
Selecciona un número de tres dígitos, con todos los dígitos diferentes entre sí, y escribe todos los números de dos dígitos posibles con esos tres dígitos (que serán seis). Entonces divide la suma de todos los números de dos dígitos obtenidos entre la suma de los dígitos del número original. ¿Qué ocurre?
Veamos qué ocurre con un ejemplo concreto. Sea el número de tres dígitos 739, que efectivamente tiene los tres dígitos diferentes. Los números de dos dígitos posibles con esos tres dígitos 3, 7 y 9 son 37, 39, 79, 73, 93 y 97. Sumamos estos números 37 + 39 + 79 + 73 + 93 + 97 = 418 y dividimos esta suma por la suma de los dígitos del número original 7 + 3 + 9 = 19, dando 418 / 19 = 22.
Como vemos el resultado es el número con el que habíamos empezado esta entrada, el 22. Pero esto puede ser casualidad. Por lo tanto, tomemos otro número, por ejemplo, 251, y veamos qué ocurre ahora. Para este número tenemos que 12 + 15 + 25 + 21 + 51 + 52 / 2 + 5 + 1 = 176 / 8 = 22. De nuevo, el número mencionado.
Da igual el número de tres dígitos que consideremos inicialmente, siempre vamos a obtener el mismo resultado, 22. Vamos a demostrar esta misteriosa propiedad.
Empecemos por un número de tres dígitos genérico abc, cuyo valor es: 100 a + 10 b + c. Tomemos los números de dos cifras que se pueden generar con ellos {ab, ac, bc, ba, ca, cb} y sumemos sus valores
(10 a + b) + (10 a + c) + (10 b + c) + (10 b + a) + (10 c + a) + (10 c + b),
que es igual a
10 (a + a + b + b + c + c) + (b + c + c + a + a + b) = 20 (a + b + c) + 2 (a + b + c),
que sacando factor común queda
22 (a + b + c),
que al dividirlo por la suma de los tres dígitos del número original a + b + c, queda claramente 22. Una vez más con un poco de algebra podemos demostrar un comportamiento misterioso de los números.
 22 Acacia Avenue es una canción del legendario álbum “The Number of the Beast” (1982) de Iron Maiden
22 Acacia Avenue es una canción del legendario álbum “The Number of the Beast” (1982) de Iron Maiden
Este comportamiento misterioso relacionado con el número 22 nos permite realizar un sencillo truco de magia. Podemos escribir una predicción (que sería el número 22) en un papel y meterla en un sobre o dársela a alguna de las personas que están con nosotros, para luego pedir a alguna otra persona que elija un número de tres dígitos (todos ellos distintos) y siga las instrucciones que le explicamos (que son las escritas arriba). El resultado de sus operaciones coincidirá con nuestra predicción, el número 22.
Hemos pedido que los dígitos del número original sean distintos, sin embargo, por la demostración anterior vemos que el resultado sigue siendo válido cuando hay dígitos repetidos en el número de tres dígitos inicial, aunque los dos dígitos iguales hay que tratarlos como si fuesen diferentes. Por ejemplo, si tomamos el número 522, cuyos tres dígitos son 2, 2, 5, tenemos que los números de dos dígitos posibles con estos son 22, 25, 25, 22, 52 y 52, luego 22 + 25 + 25 + 22 + 52 + 52 / 5 + 2 + 2 = 198 / 9 = 22.
 El dorsal 22 es el que luce el jugador del Athletic de Bilbao Raúl García. Imagen de El desmarque
El dorsal 22 es el que luce el jugador del Athletic de Bilbao Raúl García. Imagen de El desmarque
Vamos a terminar esta entrada del Cuaderno de Cultura Científica con algunas otras propiedades del número 22, además de las comentadas al principio de la entrada.
1. El número 22 es un número pancake, o número tortita, ya que la máxima cantidad de trozos de pancake, o tortita, que se pueden conseguir con 6 cortes es 22.
2. Los únicos números n para los cuales el factorial del número n! (véase la entrada Buscando lagunas de números primos [https://culturacientifica.com/2018/06/27/buscando-lagunas-de-numeros-no-primos/]) tiene n dígitos son 22, 23 y 24.
3. El 22 es un número cortés, o trapezoidal, ya que puede expresarse como suma de números naturales consecutivos, 22 = 4 + 5 + 6+ 7.
4. Es un número deficiente, ya que la suma de sus divisores propios es 1 + 2 + 11 = 14, menor que el propio número (véase la entrada Los números enamorados).
5. Es un número tal que el producto de sus dígitos 4 es igual a la suma de sus dígitos 4.
6. Su representación en la base binaria es 10110, por lo que se dice que es un número pernicioso, ya que la representación binaria contiene un número primo de unos (en este caso 3).
7. El número 22 es un número aritmético, ya que la media aritmética de sus divisores es un número entero 1 + 2 + 11 + 22 / 4 = 36 / 4 = 9. El número 24, por ejemplo, no es aritmético, ya que 1 + 2 + 3 + 4 + 6 + 8 + 12 + 24 / 8 = 60 / 8 = 7,5.
8. 22 es un número de Smith, ya que la suma de sus dígitos (2 + 2 = 4) es igual a la suma de los dígitos de sus factores primos, contados con multiplicidad (como 22 = 2 x 11, entonces 2 + 1 + 1 = 4). El número de la Bestia, 666, también es un número de Smith ya que 666 = 2 x 3 x 3 x 37 y 6 + 6 + 6 = 2 + 3 + 3 + 3 + 7.
 Portada y contraportada del albúm de Bon Iver titulado 22, A Million (2016), cuyo diseño es del artista Eric Timothy Carlson, con una gran cantidad de diseños numéricos
Portada y contraportada del albúm de Bon Iver titulado 22, A Million (2016), cuyo diseño es del artista Eric Timothy Carlson, con una gran cantidad de diseños numéricos
Bibliografía
1.- Raúl Ibáñez, La gran familia de los números, Catarata, 2021.
2.- Raúl Ibáñez, Cayley, el origen del álgebra moderna, Genios de las Matemáticas, RBA, 2017.
3.- Alfred S. Posamentier, Math Wonders to inspire Teachers and Students, ASCD, 2003.
4.- David Wells, The Penguin Dictionary of Curious and Interesting Numbers, Penguin Books, 1986.
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica
El artículo El misterioso número 22 se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Actúa localmente: tranvías eléctricos sin catenaria

El comportamiento de los océanos, la atmósfera, la superficie terrestre, la criosfera, la biosfera y el clima ya no es el mismo que ha caracterizado durante más de 11.000 años la época geológica en la que formalmente aún vivimos, el Holoceno. La especie humana ha cambiado el planeta Tierra.
Tanto es así, que el hecho de que podamos afectar de modo tan significativo el curso de la evolución geológica de nuestro planeta dio pie en 2009 a la creación del Grupo de Trabajo sobre Antropoceno para examinar la posibilidad de la formalización e inclusión de un nuevo término en la Tabla Cronoestratigráfica Internacional (conocida como la Escala del Tiempo Geológico), el Antropoceno.
Desde el punto de vista climático, el rápido aumento de los gases de efecto invernadero desde el siglo XIX ha provocado un creciente ascenso de la temperatura y del nivel del mar, acompañados por una pérdida de hielo en los continentes. Este calentamiento ha alcanzado ya niveles más altos que los detectados durante el Holoceno y se acerca a los de otras etapas interglaciares del periodo Cuaternario.
La evidencia de que es necesario empezar a actuar ya para ralentizar, si no revertir, los múltiples efectos perniciosos del cambio climático cristalizó hace ahora 5 años a nivel diplomático en en el llamado Acuerdo de París. Independientemente de ello, la consciencia ciudadana es la que está llevando a instituciones, gobiernos y empresas a adoptar medidas para reducir las emisiones de gases de efecto invernadero.
Aunque muchas veces se suele confundir en los medios de comunicación, cambio climático y contaminación no son la misma cosa. Quizás se deba a que los grandes medios residan en grandes ciudades y mezclan churras con merinas. Pero no es así. Por ejemplo, el cambio climático afecta a la aldea de mis ancestros en el norte de Salamanca, pero allí solo saben de la contaminación que es una cosa que está en Madrid, como el Bernabéu.
Con todo, en las grandes ciudades lucha contra la contaminación y lucha contra el cambio climático son la misma porque tienen la misma fuente: los motores de combustión de vehículos y las calderas de calefacción. La solución a ambos problemas pasa por el desarrollo de acumuladores de energía: en el primer caso como baterías de automóviles en sentido amplio y, en el segundo como acumuladores para, por ejemplo, paneles solares.
En las grandes ciudades el transporte público no contaminante y no emisor de gases de efecto invernadero es fundamental no solo para el cambio climático y la salud de la ciudadanía, también para la salud de los monumentos de la ciudad. Los requisitos no paran ahí. Si uno quiere un nuevo medio de transporte seguro, fiable, no contaminante y no emisor de gases de efecto invernadero, ¿por qué no añadirle además que no haga ruido y que no altere el entorno con estructuras permanentes?
Yo trabajaba en Sevilla cuando se estaban realizando las obras del llamado metro de Sevilla, un metro que en el centro de la ciudad circula en superficie. De vez en cuando los compañeros íbamos a tomar tapas a una cantina minúscula pero con excelente cocina de la zona de la catedral e, invariablemente, uno de nosotros, ingeniero por más señas, decía al ver las obras: “a ver que se inventan para las catenarias”. No hay catenarias en el metro de Sevilla en su zona monumental, y es eléctrico. Va con baterías, pero no unas cualquiera.
El desarrollo de unas baterías capaces de mover un tren durante kilómetros (más de 130 km al día, en el caso de Sevilla), con arranques y paradas, con frío en invierno (calefacción) y un calor achicharrante en verano (aire acondicionado), no es nada fácil. Dos entidades vascas colaboran en crear nuevos acumuladores que cumplan todos estas demandas: CIC energiGUNE, en los aspectos más de investigación, y CAF Power & Automation en los de desarrollo. El resultado puede apreciarse en este vídeo:
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Actúa localmente: tranvías eléctricos sin catenaria se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Actúa localmente: impresión 3D de piezas aeronáuticas de titanio
- Actúa localmente: robots inteligentes autoadaptativos para la producción industrial
- Actúa localmente: huesos a partir de ARN modificado e impresoras 3D
¿Somos la especie más inteligente del planeta?
Paul Palmqvist Barrena
 Encéfalo de la Capilla Sistina. Fuente: Flickr / Tom Blackwell
Encéfalo de la Capilla Sistina. Fuente: Flickr / Tom BlackwellPaul Palmqvist Barrena, Universidad de Málaga
A primera vista, la respuesta a esta pregunta parece sencilla. Somos la única especie que se plantea estas cuestiones, por lo que nuestra capacidad cognitiva debe rebasar con creces la de los restantes animales, ¿verdad?
Ahora bien, no deberíamos abordar el tema sin formular antes otra cuestión: ¿cómo podemos definir –y medir– la inteligencia? Según observó Homero en el libro octavo de la Odisea, “la inteligencia es un regalo de la gracia que no todos los hombres poseen”. Y aunque esta afirmación sigue siendo válida hoy día, la verdad es que no nos aclara el asunto.
Ya en la década de los años veinte del siglo pasado, el psicólogo experimental Edwin Boring opinaba que “inteligencia es lo que miden los tests de inteligencia”. En los setenta, Ulric Neisser, considerado el padre de la psicología cognitiva, escribía que “inteligencia es la suma de los atributos de una persona prototípicamente inteligente”.
Aun suponiendo un razonamiento circular, la última definición goza de cierto consenso: presumimos de saber qué personas son inteligentes y, en consecuencia, aceptamos como medida de su inteligencia lo que nos permite identificarlas.
Es frecuente que los genios se reconozcan, admiren y respeten, aunque provengan de disciplinas diferentes. Fue el caso de Buñuel, Dalí y Lorca, entre otros exponentes de la Edad de Plata de la cultura española, al coincidir en la madrileña Residencia de Estudiantes.
Los tests de inteligencia
Los tests de inteligencia nacieron a comienzos del siglo XX gracias al trabajo del pedagogo Alfred Binet y el psiquiatra Théodore Simon. Diseñados con la vocación de identificar alumnos con dificultades de aprendizaje, se convirtieron rápidamente en un sistema estándar para medir la inteligencia.
Ahora bien, a diferencia de otras magnitudes físicas, como el peso o la altura, la inteligencia no consta de una única dimensión. Esto hizo necesario diseñar baterías de tests para evaluar diversas funciones cognitivas. Por ejemplo, factores de inteligencia verbal, razonamiento analógico y visualización espacial.
Al correlacionarse bien las puntuaciones en estos factores y ser estables con la edad, se pensó que podrían medir un “factor general de inteligencia” subyacente, como intentaron el test Stanford-Binet o la escala de inteligencia para adultos de Wechsler.
Algunos de los aspectos que miden los tests son intrínsecos a los individuos: el caso de la memoria a corto plazo, la capacidad de razonamiento deductivo o la habilidad para detectar y manipular patrones en diseños geométricos y espaciales. En cambio, otros no están libres de influencias culturales, como los que tratan del conocimiento del mundo y el uso de vocabulario.
De hecho, no podemos entender la inteligencia humana fuera de su contexto cultural y ambiental.
Por ejemplo, el corredor de bolsa que triunfa en el entorno agresivo de Wall Street y el cazador-recolector bosquimano que sobrevive en el inhóspito desierto del Kalahari son prototipos de personas inteligentes y bien aclimatadas. Pero si intercambiasen sus vidas, el resultado previsible sería desastroso, como mostraba la película “Los dioses deben estar locos”. Al fin y al cabo, los “rasgos adaptativos” que asociamos a sus inteligencias tienen poco sentido fuera de sus respectivos entornos culturales.
La inteligencia en el Reino Animal
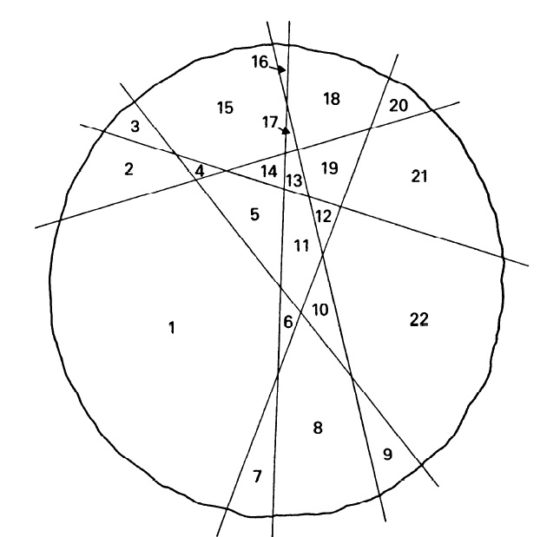
Existen organismos con notables habilidades cognitivas, tanto comparados con otros de su grupo como por su capacidad de resolver situaciones ajenas a su medio natural. Es el caso de los simios, los delfines, los elefantes, las hienas, los cuervos, los loros y las lechuzas. Todos ellos destacan por su desarrollo cerebral y por sus relaciones sociales complejas.
Entre los invertebrados llaman la atención sobre todo los pulpos y algunos himenópteros, como las hormigas, en las que conviene distinguir entre inteligencia “individual” y “colectiva”.
Cerebros de hormigas e inteligencia colectiva
El cerebro de una hormiga tiene unas 250 000 neuronas, cifra minúscula en comparación con los cien mil millones que alberga un cerebro humano. Pese a ello, sus colonias muestran comportamientos muy elaborados. Tanto, que desarrollaron la agricultura (jardines de hongos subterráneos) y la ganadería trashumante (pastoreo de pulgones) millones de años antes que la humanidad.
En particular, las especies guerreras esclavistas muestran tácticas de combate y decisiones estratégicas tan complejas como en los ejércitos humanos. El estudio de sus movimientos ha permitido desarrollar algoritmos matemáticos que simulan estrategias óptimas en el campo de batalla.
Esto nos lleva a plantearnos hasta qué punto emerge una “inteligencia colectiva superior” de la suma de comportamientos individuales de las hormigas, que funcionan como autómatas en respuesta a instrucciones químicas (feromonas) e interacciones sociales muy sencillas.
En el caso humano –a diferencia de los insectos sociales– habría que sumar el componente de maduración de los mecanismos cognitivos. La integración de los conocimientos y experiencias pasadas determina y condiciona nuestro aprendizaje. Parafraseando a Marie von Ebner-Eschenbach, “en la juventud aprendemos, mientras que en la madurez comprendemos”, algo extensible a simios, delfines y elefantes.
El coeficiente de encefalización
El tamaño del encéfalo ha recibido mucha atención por los antropólogos y zoólogos dada su correlación con el repertorio de habilidades cognitivas que observamos en el Reino Animal. Ahora bien, no se trata de sus dimensiones absolutas, sino de su relación alométrica con el tamaño de los animales.
El especialista en neurociencias Harry Jerison fue pionero en los setenta al estimar dicha relación mediante el ajuste por regresión entre los logaritmos de las masas corporal y cerebral en los vertebrados. Su enfoque comparativo, que se muestra para los mamíferos en la gráfica adjunta, estableció el ritmo al que aumentan las dimensiones del encéfalo según lo hace el tamaño del cuerpo.
Esto permitió estimar el volumen cerebral esperable por unidad de masa corporal. Y así, calcular el coeficiente de encefalización de cada especie a partir del cociente entre masa cerebral observada y estimada en el ajuste.
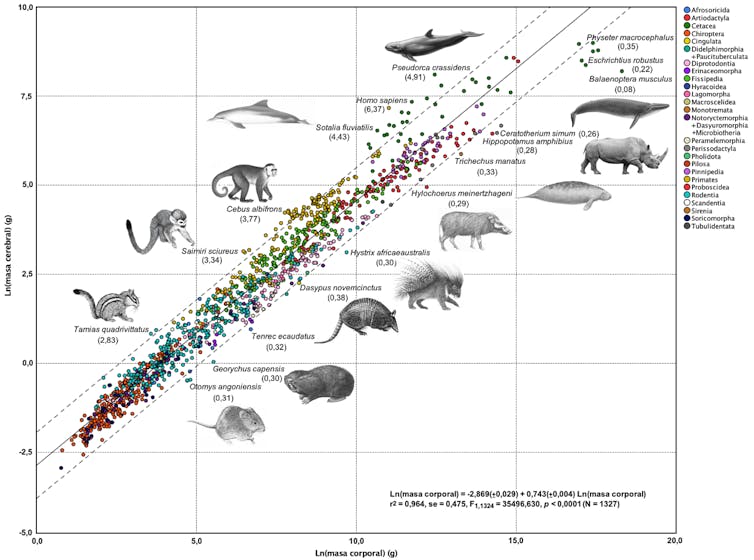 Coeficiente de encefalización en 1327 especies de mamíferos, identificadas según órdenes (leyenda en la parte superior derecha). Se muestran los valores numéricos obtenidos para diversas especies al dividir sus masas cerebrales por las estimadas con el ajuste. Figura elaborada por el autor a partir de datos recopilados de la bibliografía.
Coeficiente de encefalización en 1327 especies de mamíferos, identificadas según órdenes (leyenda en la parte superior derecha). Se muestran los valores numéricos obtenidos para diversas especies al dividir sus masas cerebrales por las estimadas con el ajuste. Figura elaborada por el autor a partir de datos recopilados de la bibliografía.En la figura se aprecia que los primates, el orden de mamíferos al que pertenecemos, tienden a situarse por encima de la recta de regresión. Esto indica que sus cerebros son de mayor tamaño que los de otras especies de masa similar.
Igual ocurre con los cetáceos que conservan los dientes (odontocetos). Por el contrario, los que tienen barbas para filtrar (misticetos) presentan encéfalos comparativamente reducidos, como se aprecia en la ballena azul (Balaenoptera musculus), el animal más grande de la Tierra. En ella, el coeficiente de encefalización toma el valor 0,08 (esto es, el volumen de su cerebro es solo el 8% del esperable para un animal de su tamaño).
Nuestra especie (Homo sapiens) presenta la encefalización más elevada entre los mamíferos, con un cerebro 6,4 veces mayor del calculado para una especie de nuestras dimensiones. Las siguientes son la falsa orca (Pseudorca crassidens, 4,9) y el delfín gris de río (Sotalia fluviatilis, 4,4).
Curiosamente, los hominoideos (chimpancés, gorilas y orangutanes), nuestros parientes vivos más próximos, no presentan los valores más altos de encefalización entre los primates. Este puesto corresponde a dos especies americanas: el capuchino de frente blanca (Cebus albifrons, 3,8) y el mono ardilla (Saimiri sciureus, 3,3).
Entonces, ¿se trata solo de tener un cerebro muy grande o hay algo más? El cerebro humano, una versión a mayor escala del de otros primates, presenta una densidad neuronal muy superior a la de un roedor. Concretamente 7,5 veces más neuronas por gramo de tejido cerebral y 12,5 veces más en el córtex prefrontal, donde se localizan las funciones cognitivas superiores.
Tenemos, pues, un cerebro con 100 000 millones de neuronas densamente empaquetadas, acompañadas por un billón de células gliales y enlazadas por 1 000 billones de conexiones sinápticas.
Nuestra arquitectura cerebral explica por qué somos la especie más inteligente del planeta, algo que debería imponernos más racionalidad en la gestión de sus recursos naturales y su biodiversidad. En eso, al menos hasta ahora, no hemos sido lo suficientemente “listos” y responsables.![]()
Sobre el autor: Paul Palmqvist Barrena es catedrático de paleontología de la Universidad de Málaga
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo ¿Somos la especie más inteligente del planeta? se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La evolución nos dice que es probable que seamos la única vida inteligente del universo
- ¿Jugar al ajedrez te hace más inteligente? Un vistazo a las pruebas
- ¿Por qué somos supersticiosos?
En el control de la inteligencia artificial nos jugamos el futuro
Antonio Diéguez Lucena
 Foto: Conor Luddy / Unsplash
Foto: Conor Luddy / Unsplash
Los avances en inteligencia artificial (IA) y en biotecnología, exacerbados en la imaginación popular por el discurso transhumanista, han propiciado que la gobernanza de la tecnología se haya convertido en un problema ineludible en la agenda política. Quizás ya no suene melodramático decir que se trata de un asunto en el que nos jugamos el futuro.
Seguimos, sin embargo, con instituciones y sistemas regulatorios que, a lo sumo, son funcionales en relación con la tecnología de la tercera revolución industrial (revolución digital e informacional), pero que resultan obsoletos para regular las tecnologías de la cuarta (unión de tecnologías digitales, particularmente la IA y las redes de sistemas inteligentes, la robótica, el internet de las cosas, las tecnologías de nuevos materiales, la nanotecnología y las biotecnologías). Esta revolución, a juicio de importantes analistas, ha comenzado ya.
Como bien explica el filósofo Luciano Floridi en su libro The fourth revolution, el reto que tenemos ante nosotros no es tanto el que puedan presentar las innovaciones tecnológicas como tales, sino el que plantea la propia gobernanza de lo digital. Sin embargo, buena parte de la sociedad parece no tomarse demasiado en serio este problema. Algunos legisladores y expertos son conscientes de la magnitud del desafío, pero hay dudas razonables de que puedan ejercer una influencia decisiva en el plano legal e institucional con la premura que sería exigible.
¿De verdad existe una inteligencia artificial?
Hasta el presente, todos los logros en el campo de la inteligencia artificial han sido en el desarrollo de lo que se conoce como “inteligencia artificial particular”, específica o estrecha. Es decir, en la creación de sistemas computacionales que despliegan una gran capacidad, superior incluso a la humana, para realizar tareas muy específicas y bien definidas. Por ejemplo, jugar a un juego con reglas fijas (ajedrez, go, damas, videojuegos), responder a preguntas de cultura general, realizar diagnósticos médicos precisos (enfermedades infecciosas, tipos de cáncer, medicina personalizada), reconocer caras y otras imágenes, procesar e interpretar la voz humana, traducir de un idioma a otro.
En realidad, una parte sustancial de lo que hoy llamamos inteligencia artificial son sistemas de minería de datos, llamados así porque son capaces de analizar cantidades masivas de datos y obtener de ellos patrones desconocidos y lo que podríamos considerar como conocimiento nuevo sobre esos datos.
Por impresionantes que sean estos logros, estas tecnologías no alcanzan la versatilidad y flexibilidad de la inteligencia humana. Los sistemas más inteligentes de los que disponemos en la actualidad no pueden ser utilizados con eficacia en tareas diferentes a aquellas para las que fueron programados. Hay quienes piensan que ni siquiera los deberíamos llamar inteligentes, puesto que la única inteligencia que aparece en ellos es la del programador humano o la de los seres humanos en cuyo contexto social estos sistemas cumplen alguna función.
Se suele decir que una máquina es inteligente cuando es capaz de realizar tareas tales que asumimos que requieren de inteligencia para ser llevadas a cabo. Esta es una definición operativa, puesto que considera que la inteligencia artificial se caracteriza como inteligente por sus resultados. No obstante, la propia caracterización de la inteligencia es un viejo problema cuya discusión continúa. No es fácil dirimir la cuestión, por lo que no es extraño que tampoco haya acuerdo sobre cómo definir la propia inteligencia artificial.
Aceptemos, sin embargo, que en un sentido no meramente metafórico podemos hablar de inteligencia artificial. ¿Debemos entonces temer la creación de una Inteligencia Artificial General (IAG)? ¿Tendremos máquinas superinteligentes que tomarán el control de todo el planeta o seremos capaces de controlarlas nosotros? Son preguntas que se repiten a menudo cuando se menciona el futuro de la IA en los medios de comunicación y en los libros de divulgación, y creo que merecen ser tomadas en serio.
La inteligencia artificial ya es un desafío
No conviene olvidar que, con independencia de si el desarrollo futuro de una inteligencia superior a la humana pudiera representar un peligro para la supervivencia de nuestra especie, lo que por el momento constituye un desafío desde el punto de vista de la salvaguarda de los derechos de las personas son ciertas aplicaciones de la IA cuyos efectos se están viendo ya, como es el caso del uso de nuestros datos personales por parte de sistemas de IA pertenecientes a las grandes empresas tecnológicas, cuyo poder a su vez se acrecienta aceleradamente, o los sesgos y opacidad de los algoritmos usados en la toma de decisiones importantes para la vida de las personas, como la contratación de personal en las empresas o la concesión de créditos bancarios.
Mención aparte merecen los peligros del uso de la IA en la identificación de rostros y en la búsqueda de delincuentes y prevención del delito, en la vigilancia y represión de disidentes políticos, en la creación de armas autónomas, o en la proliferación de los ciberataques, de las noticias falsas y de la desestabilización política mediante la desinformación.
Digamos también, para no dejar una imagen completamente negativa, que la IA está siendo un instrumento muy eficaz en la persecución de delitos financieros, en la protección de la seguridad de las personas, en la potenciación del progreso biomédico, en el logro de una mayor eficiencia energética y en la protección el medio ambiente.
Creo que, para analizar las consecuencias posibles de la inteligencia artificial, tanto favorables como desfavorables, discutir si se trata de inteligencia genuina, similar a la humana, con posibilidad de ser consciente o no, es desviar el foco del auténtico problema.
Lo que me parece que debería preocuparnos ahora no es si podremos crear inteligencia similar a la humana o superior, sino qué podrán hacer con nosotros las máquinas que creemos en el futuro, si es que estas tienen capacidad para tomar decisiones que se consideren en la práctica como inapelables en su autoridad. No es cómo piensen esas máquinas lo que importa, es cómo actúen, puesto que serán agentes con una cierta autonomía, y, sobre todo, cómo las insertaremos en nuestra ordenación social.
Lo relevante en todo esto será que los seres humanos acepten sin supervisión las decisiones que forjen dichas máquinas, así como las consecuencias que esas decisiones puedan tener sobre nuestras vidas, sobre todo si el propio ser humano cede el control.
En definitiva, es necesario promover instituciones y procedimientos que faciliten la defensa de los derechos de los ciudadanos frente a los riesgos potenciales de la inteligencia artificial, como, por ejemplo, la defensa del derecho a la privacidad, así como comenzar a pensar en los requisitos que serían fundamentales para un control efectivo de la IA, porque frente a lo que algunos nos dicen, no hay a priori ninguna razón incontestable para aceptar que el problema del control de la IA sea irresoluble.![]()
Sobre el autor: Antonio Diéguez Lucena es catedrático de Lógica y Filosofía de la Ciencia en la Universidad de Málaga
Este artículo fue publicado originalmente en The Conversation. Artículo original.
El artículo En el control de la inteligencia artificial nos jugamos el futuro se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- La búsqueda de la inteligencia artificial, en la próxima zientziateka
- Máquinas inteligentes (II): Inteligencia artificial y robótica
- La búsqueda de la inteligencia artificial
Eva Ferreira – Naukas Bilbao 2019: Hacer predicciones es muy difícil, sobre todo las del futuro
 Eva Ferreira. Foto: Iñigo Sierra
Eva Ferreira. Foto: Iñigo SierraHacer predicciones cuando en ellas las personas son un factor importante, se puede llegar a hacer muy complicado. Las personas no somos cometas. ¿Quién le hubiera dicho a Eva Ferreira cuando dio esta charla en 2019 que en 2021 iba a ser la rectora de la UPV/EHU?
Eva Ferreira es matemática de formación y catedrática de economía aplicada y profesora de estadística en la Facultad de Ciencias Económicas y Empresariales de la UPV/EHU.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo Eva Ferreira – Naukas Bilbao 2019: Hacer predicciones es muy difícil, sobre todo las del futuro se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Raúl Ibáñez – Naukas Bilbao 2019: Teorías fantásticas sobre las grafías de los números
- Naukas Bilbao 2017 – Raúl Gay: Todo sobre mi órtesis
- Clara Grima – Naukas Bilbao 2019: Mathematical Rhapsody
ADN nuclear de varios individuos neandertales a partir de sedimentos
 © Javier Trueba. Madrid Scientific Films
© Javier Trueba. Madrid Scientific FilmsLa menos conocida de las galerías de la Cueva Mayor en la Sierra de Atapuerca es la llamada Galería de las Estatuas. El nombre le viene de unas grandes estalagmitas que se formaron allí gota a gota hace más de un millón de años. A esas formaciones calcáreas se les atribuía la capacidad de hablar y aparecen en crónicas antiguas haciendo profecías. En la “Descripción de la Cueva llamada de Atapuerca” de los ingenieros Sampayo y Zuaznávar (1868) pueden verse grabados de las “estatuas”.
 Ilustración de la Sala de las Estatuas publicada en «Descripción con planos de la cueva llamada de Atapuerca» (Sampayo y Zuaznávar, 1868).
Ilustración de la Sala de las Estatuas publicada en «Descripción con planos de la cueva llamada de Atapuerca» (Sampayo y Zuaznávar, 1868).Esta galería se comunicaba con el exterior en la época de los neandertales, pero luego la boca se rellenó y la cavidad quedó aislada, de manera que cuando llegaron los H. sapiens a Atapuerca ya no pudieron entrar y ver las viejas columnas. A este lugar se accede ahora por el interior de la Cueva Mayor.
Finalmente, sobre el lugar donde habían vivido los neandertales se formó un suelo estalagmítico, es decir, una gruesa plancha de calcita, que selló para siempre el yacimiento.
En las excavaciones que se realizan desde el año 2008 en la Galería de las Estatuas se han recuperado restos de los animales consumidos por los neandertales y sus herramientas líticas, además de una falange de pie indiscutiblemente neandertal.
Debido a su total aislamiento, los sedimentos del yacimiento de la Galería de las Estatuas han mantenido constantes sus condiciones de humedad y de temperatura y no han sufrido ninguna alteración por agentes naturales o por intervenciones humanas modernas, lo que hace de Estatuas el yacimiento perfecto para excavar.
El equipo de Atapuerca mantiene una colaboración de años con Matthias Meyer, investigador senior del grupo de genética evolutiva del Instituto Max Planck de Antropología Evolutiva que dirige Svante Pääbo (Premio Princesa de Asturias) en Leipzig. Esta larga colaboración ha producido resultados espectaculares en el yacimiento de la Sima de los Huesos, que también se localiza en la Cueva Mayor. El ADN mitocondrial y el ADN nuclear humanos más antiguos se han recuperado en la Sima de los Huesos a partir de fósiles.
El ADN mitocondrial se encuentra en las mitocondrias, que son unos orgánulos que producen la energía de la célula. Es más fácil secuenciar completo el ADN mitocondrial que el ADN nuclear porque hay muchas mitocondrias en cada una de las células del cuerpo, y porque su longitud es de solo 16.000 pares de bases (las “letras” de la secuencia de ADN). El ADN nuclear es el de los cromosomas. Solo se encuentra en el núcleo celular y es mucho más largo: 3.200 millones de pares de bases. El ADN mitocondrial se trasmite solo por vía materna, mientras que el ADN nuclear se trasmite por vía paterna y materna. Estas razones hacen que el ADN nuclear sea mucho más informativo que el mitocondrial, pero al mismo tiempo enormemente más difícil (y costoso) de secuenciar.
 © Javier Trueba. Madrid Scientific Films
© Javier Trueba. Madrid Scientific FilmsRecientemente, el equipo dirigido por Matthias Meyer ha explorado la posibilidad de obtener ADN directamente de los sedimentos, sin necesidad de tomar muestras en huesos humanos, que faltan en la mayoría de los yacimientos. En un artículo anterior se demostró que era posible recuperar ADN mitocondrial de los sedimentos, pero faltaba conseguirlo con el ADN nuclear.
La temperatura es un factor de primer orden en la conservación de la molécula de ADN: a mayor temperatura, mayor degradación de la molécula. Por eso, cuanto más al norte esté el yacimiento, mejor será la conservación. Siberia es el lugar ideal para recuperar ADN antiguo pero, por sus especiales características, la Galería de las Estatuas ofrecía una oportunidad única de obtener ADN procedente del sedimento en una región situada en latitudes templadas.
En el artículo que se publica en Science, liderado por Benjamin Vernot, del equipo de Matthias Meyer, se informa de la obtención de ADN mitocondrial y ADN nuclear en dos yacimientos de los montes Altai en Siberia (cuevas Denisova y Chagyrscaya), y también en la Galería de las Estatuas de la Cueva Mayor. Esta publicación puede sin lugar a dudas calificarse de histórica, porque abre de par en par la puerta a futuras investigaciones. Ya no hacen falta fósiles humanos para identificar a los moradores de una cueva prehistórica.
Siempre, claro está, que las condiciones de conservación sean tan buenas como las de la Galería de las Estatuas… y siempre que la excavación se haga de forma extremadamente cuidadosa para que no se alteren esas condiciones. Y en efecto, en Estatuas se ha excavado todos estos años pensando en esa posibilidad, por lo que se ha renunciado a desobstruir la entrada de la Galería y comunicarla con el exterior. Esta estrategia de excavación, la de acceder al yacimiento realizando un largo recorrido por el interior de la cueva, ha hecho que la tarea sea más complicada, pero el artículo de Science demuestra que ha merecido la pena el esfuerzo. Desde el año 2020 se excava también la parte del yacimiento que quedó al otro lado del “tapón” de la entrada, en lo que ahora es la ladera de la sierra, con resultados muy interesantes.
 © Javier Trueba. Madrid Scientific Films
© Javier Trueba. Madrid Scientific Films¿Qué nos dice el ADN de los neandertales de la Galería de las Estatuas? Para empezar se ha recuperado en los sedimentos tanto ADN nuclear como ADN mitocondrial de varios individuos. El ADN del individuo más antiguo perteneció a un varón neandertal de raigambre antigua. Está datado en aproximadamente 110.000 años, pero su estirpe se originó antes, hace unos 130.000 años. La fecha que se ha calculado para esa “radiación” (que es como se llama técnicamente a un conjunto de líneas que se separan de un antepasado común) coincide con el inicio del último periodo cálido entre dos glaciaciones. Puede que la radiación y la mejoría climática tengan algo que ver, porque los grandes cambios ambientales producen grandes cambios ecológicos, que afectan a la evolución de muchas especies.
 Falange neanderthal. © Javier Trueba. Madrid Scientific Films
Falange neanderthal. © Javier Trueba. Madrid Scientific FilmsAlgunos miles de años después nos encontramos en la Galería de las Estatuas unos neandertales genéticamente diferentes, pertenecientes a una segunda radiación. De estos neandertales nuevos que sustituyeron a los antiguos se ha identificado a lo largo de la secuencia estratigráfica el ADN de por lo menos cuatro mujeres. Las más modernas se datan en unos 80.000 años. El clima ha cambiado para entonces, porque ya ha empezado el último ciclo glaciar. De nuevo la relación entre clima y evolución humana es muy sugerente.
Los neandertales de la última glaciación se conocen informalmente como “clásicos”. Son los más estudiados y los que presentan los rasgos más exagerados. Además hay una característica de los neandertales “clásicos” que es muy importante: tuvieron los cerebros más grandes de toda la evolución humana, más grandes incluso que los nuestros.
En esta investigación han participado, por parte de la Universidad del País Vasco, Arantza Aranburu y Asier Gómez-Olivencia, investigadores del Departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU.
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo ADN nuclear de varios individuos neandertales a partir de sedimentos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Nuevos neandertales del País Vasco (y algunos que dejan de serlo)
- Bioóleo a partir de residuos cítricos
- Hidrógeno a partir de composites de fibra de carbono
El jerbo que come hierbajos salados y apenas tiene agua para beber
 Psammomys obesus. Ilustración: María Lezana
Psammomys obesus. Ilustración: María LezanaPsammomys obesus, ese es el nombre científico de un jerbo que vive en el noreste de África y el Oriente próximo; se distribuye desde Argelia hasta las regiones de las dos orillas del Mar Rojo. La llaman “rata obesa”, aunque, de hecho, no es una rata, y en cuanto a lo de “obesa”, veremos más adelante que eso depende de las circunstancias. Lo que sí podemos decir es que es bien conocido por los especialistas en algunos campos de la biomedicina.
Vive en lugares relativamente desérticos, donde hay muy poca vegetación y menos agua. Su principal alimento consiste en Atriplex halinus, un matorral que crece en tierras con alto contenido salino, donde ninguna otra planta puede vivir. Se alimenta de las hojas de ese matorral y excava sus huras en sitios donde abundan. Atriplex es una planta de muy escaso valor nutricional; de hecho, la rata obesa es el único animal del que se sabe que la consume en el desierto. Por vivir donde vive, en un medio tan extremo, Psammomys no tiene competidores.
Es un animal muy poco activo. Se podría decir que, como no hay ningún otro animal que compita con ella por el alimento, puede permitirse el lujo de vivir “despacio”. Viviendo así gasta poca energía y eso le conviene, por vivir en un medio muy cálido, ya que en un medio tal, no es fácil disipar el calor que se produce cuando se despliega mucha actividad.
Como he señalado antes, los matorrales que consume la rata obesa son de muy escaso valor nutricional. Esa es, seguramente, otra razón por la que le viene bien la quietud. Pero desgraciadamente para Psammomys, eso tiene una consecuencia muy negativa: cuando se mantiene en cautividad engorda con mucha facilidad, y no solo eso, además padece diabetes de tipo II, que es la que se sufre como consecuencia de una dieta y hábitos alimenticios inadecuados. Eso es lo que le ocurre al pobre jerbo por cambiarle la dieta, pues en los laboratorios lo alimentan con piensos y cereales. Por esa razón, la rata obesa es muy utilizada, como modelo biológico, en las investigaciones sobre obesidad y diabetes. En la actualidad solo se crían en cautividad ejemplares pertenecientes a dos linajes; de hecho, es muy difícil mantenerlos en el laboratorio, ya que mueren con facilidad por culpa, precisamente, de la diabetes.
Donde vive la rata obesa la única agua que puede beberse es la del rocío que queda al amanecer en los matorrales. Por eso los lame en ese momento, antes de que se sequen; es su única bebida. Además, aprovecha toda el agua que puede de los tejidos de la planta, que es muy poca. Está, por ello, obligada a economizarla al máximo.
El mecanismo más poderoso para economizarla consiste en reabsorber en los riñones gran parte del plasma que se ha filtrado en los glomérulos renales; la orina que producen tiene, por esa razón, una concentración muy alta de solutos. Psammomys produce una orina que es 17 veces más concentrada que la sangre. Es un valor altísimo. En la rata canguro, otro pequeño mamífero muy bien adaptado a la vida en zonas séricas, la concentración urinaria de solutos es 14 veces más alta que la sanguínea, algo más baja que la del jerbo. Esa diferencia tiene que ver, seguramente, con la dieta, ya que Atriplex halimus tiene un alto contenido en sales. Así pues, el riñón no solo debe hacerse cargo de un intenso trabajo en economizar agua, sino que debe expulsar las sales que inevitablemente incorpora con la dieta, lo que constituye una severa dificultad añadida.
Psammomys obesus tiene que hacer frente a unas condiciones durísimas en su medio natural. Pero sacarlo de los desiertos en que habita y llevarlo a un laboratorio no mejora en absoluto sus condiciones de vida. Sustituye los rigores propios de la ausencia de agua por la maldición de la obesidad y la diabetes a que le aboca una alimentación mucho más rica que la que le proporcionan los hierbajos salinos del desierto.
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo El jerbo que come hierbajos salados y apenas tiene agua para beber se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Una proteína humana para potabilizar agua
- Los animales que respiran en agua
- Marcas de agua digitales, qué son y para qué sirven
Annie Russell Maunder: la Lady Computer que fotografiaba el Sol
Poseedora de todos los requisitos para el profesionalismo, excepto el género correcto, no solo era una ayudante de Walter, sino también una importante contribuyente a la astronomía por derecho propio. […] La formación matemática básica de Annie Maunder, las reflexivas publicaciones, la edición de revistas y la pertenencia a organizaciones profesionales dejan claro que ella era una participante de pleno derecho en la comunidad astronómica.
Marilyn Ogilvie (traducción libre de [4]).
Annie Scott Dill Russell nació el 14 de abril de 1868 en Irlanda del Norte. Realizó sus estudios secundarios en el Ladies’ Collegiate School de Belfast. Allí, en 1886, ganó el premio a la excelencia académica, lo que le permitió ir a estudiar matemáticas alGirton College de la Universidad de Cambridge. Aunque fue la alumna más destacada de su promoción, al finalizar sus estudios en 1889 y debido a las reglas discriminatorias de esos tiempos, no le concedieron su grado académico.
 Annie Russell Maunder. Imagen Wikimedia Commons.
Annie Russell Maunder. Imagen Wikimedia Commons.
Russell comenzó a enseñar matemáticas en el Ladies’ High School de la isla de Jersey, pero no encontraba satisfactorio su trabajo. Su oportunidad de cambiar de actividad no tardó en llegar.
El astrónomo William Christie (1845-1922), director del Real Observatorio de Greenwich entre 1881 y 1910, decidió contratar a mujeres para realizar cálculos astronómicos ante la falta de personal. Las conocidas como Lady Computers fueron empleadas entre 1890 y 1895; las cuatro primeras fueron Isabella Jane Clemes, Alice Everett (1865-1949), Harriet Maud Furniss y Edith Mary Rix (1866-1918). Se incorporaron el 14 de abril de 1890. Alice Everett, quien fue compañera de Annie en Cambridge, la avisó de la posibilidad de encontrar trabajo en el Observatorio. Russell, junto a otras mujeres, se unió en 1891. A pesar de que todas ellas tenían más edad y una formación superior a la de sus compañeros varones, su salario y sus condiciones laborales eran las mismas y apenas las permitían sobrevivir.
Annie fue asignada al Departamento Solar, donde trabajó a las órdenes del astrónomo Edward Walter Maunder (1851-1928), con quien se casaría en 1995. Russell tenía como tarea fotografiar manchas solares y registrar su posición y su tamaño. Durante el primer año de trabajo de Annie en Greenwich, el número de observaciones registradas en el Departamento Solar superó siete veces la cantidad media de registros de los anteriores 35 años.
Al casarse con Maunder, Annie tuvo que renunciar a su puesto en el Real Observatorio de Greenwich ya que las mujeres casadas no podían ejercer cargos públicos. Ella y Alice Everett fueron aceptadas en la British Astronomical Association, fundada por Maunder, que empleaba a astrónomos poco experimentados. Annie trabajó como editora del diario de esta asociación.
Aunque el matrimonio no tuvo hijos propios, Annie cuidó a los cinco hijos (entre 7 y 21 años en el momento de casarse) de Maunder, que había enviudado en 1888. A pesar de sus numerosas tareas domésticas, Annie continuó con su trabajo astronómico colaborando con Walter. Lamentablemente, sus aportaciones no fueron lo suficientemente reconocidas.
El matrimonio Maunder realizó en 1898 una expedición a la India para captar eclipses. Allí Annie realizó fotografías del cielo con una cámara gran angular, diseñada por ella misma, que pudo construir gracias a una subvención del Girton College. En principio, la cámara estaba diseñada para observar la Vía Láctea, pero gracias a su amplitud Annie consiguió capturar la corona del eclipse del 22 de enero de 1898, alcanzando los diez millones de kilómetros.
Annie participó en otras dos expediciones para observar eclipses, una a Argel en 1900 y después otra a Mauricio en 1901. Las fotografías que realizó ayudaron a conocer mejor el comportamiento de la corona solar.
 Annie Russell Maunder en la azotea del Hotel de la Régence (Argel) con su cámara. Imagen: Wikimedia Commons.
Annie Russell Maunder en la azotea del Hotel de la Régence (Argel) con su cámara. Imagen: Wikimedia Commons.
Entre otros muchos proyectos, Annie se involucró en las investigaciones históricas de Walter que buscaban documentar una época de actividad solar anormalmente baja en la segunda mitad del siglo XVII y principios del XVIII. En efecto, entre 1645 y 1715 —intervalo denominado mínimo de Maunder— las manchas solares casi desaparecieron de la superficie solar, como observaron los astrónomos de esa época. Durante un período de 30 años dentro del mínimo de Maunder, se observaron unas 50 manchas solares, cuando lo habitual es percibir entre 40 000-50 000 manchas.
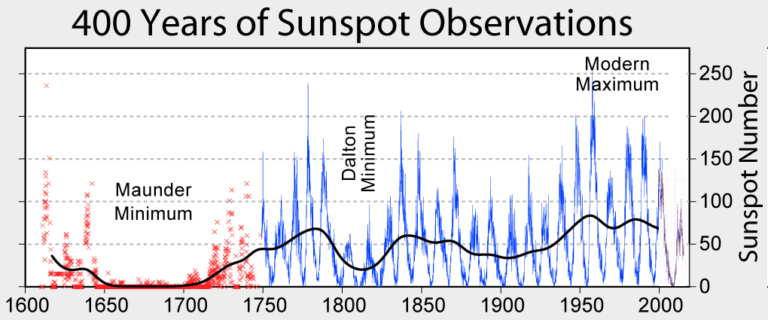 El mínimo de Maunder en 400 años de actividad solar medida por el número de manchas solares. Imagen: Wikimedia Commons.
El mínimo de Maunder en 400 años de actividad solar medida por el número de manchas solares. Imagen: Wikimedia Commons.
En 1907 Annie creó un catálogo de 600 grupos de manchas solares recurrentes, basándose en los datos obtenidos durante su contrato en el Real Observatorio de Greenwich. Y un año más tarde, con Walter como coautor, publicó The Heavens and their Story, reconociendo el propio Maunder a Annie como autora principal. Escrito de manera divulgativa para un público no experto, incluía sus fotografías del Sol y la Vía Láctea en un intento de atraer a más personas hacia la astronomía.
En 1916, finalmente, fue aceptada como miembro de la Royal Astronomical Society, 24 años después de haber rechazado su primera nominación: fue una de las primeras mujeres en conseguirlo.
Annie Russell Maunder falleció el 15 de septiembre de 1947. En su honor y en el de su marido se nombró el cráter Maunder —un cráter de impacto situado en la cara oculta de nuestro satélite—: Annie es una de Las mujeres de la Luna.
 Cráter Maunder. Wikimedia Commons.
Cráter Maunder. Wikimedia Commons.
Referencias:
[1] Daniel Roberto Altschuler Stern Fernando J. Ballesteros Roselló, Las mujeres de la Luna. Historias de amor, dolor y valor, Next Door Publishers, 2016
[2] M.T. Bruck, Lady Computers at Greenwich in the Early 1890s, Quarterly Journal of the Royal Astronomical Society 36 (1995) 83-95
[3] M. T. Bruck, Alice Everett and Annie Russell Maunder torch bearing women astronomers, Irish Astronomical Journal 21 (3/4) (1995) 280-291
[4] I J Falconer, J G Mena, J J O’Connor, T S C Peres, E F Robertson, Annie Scott Dill Maunder, MacTutor History of Mathematics archive, University of St Andrews
[5] Ziortza Guezuraga, Mirando al sol, Annie Russell Maunder, Mujeres con ciencia, Vidas científicas, 17 mayo 2017
[6] Wikipedia
Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad
El artículo Annie Russell Maunder: la Lady Computer que fotografiaba el Sol se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Vida de Galileo
- Personas famosas que estudiaron matemáticas: literatura y cine
- Henri Cartan, un “bourbakista” especialista en teoría de haces
Actúa localmente: simulaciones hiperrealistas
 Foto: Joshua Coleman / Unsplash
Foto: Joshua Coleman / UnsplashEn un futuro distópico la humanidad está atrapada sin saberlo dentro de una realidad simulada, Matrix, que las máquinas inteligentes han creado para distraer a los humanos mientras usan sus cuerpos como fuente de energía. Esta era la base de Matrix, la película de las Wachowskis de 1999. Si bien el argumento no parece muy eficiente desde el punto de vista termodinámico su impacto cultural es evidente, incorporándose el título de la película al lenguaje popular para significar que se vive en un mundo inventado y separado de la realidad.
Sin embargo, la idea de que vivimos en una simulación no es nueva en absoluto. Desde la ilusión del mundo del hinduismo (maya) y el sueño de Zhuang Zhou ser una mariposa taoísta, pasando por la caverna de Platón hasta llegar al genio maligno (malin génie) de Descartes, el Dios de Berkeley y el murciélago en la cubeta, la tentanción solipsista del escéptico, el concepto de que lo único que existe es mi consciencia y algo que le da información, es una constante histórica.
La idea de que todo nuestro universo no es más que una simulación en un ordenador de una civilización hiperavanzada no es fácilmente descartable. Solo aplicando la navaja de Ockham podríamos aventurarnos a sugerir que no parece muy probable. Con todo, Nick Bostrom publicó un artículo en 2003 en la revista Philosophical Quarterly titulado “¿Vives en una simulación por ordernador?” que dio paso a todo un movimiento metafísico, que no epistemológico, que afirma la realidad de esa simulación, el “simulismo”.
Curiosamente los humanos tendemos a comparar las cosas con aquellas que ya conocemos. Si nuestro conocimiento avanza con el tiempo, nuestras comparaciones lo hacen en paralelo. El típico ejemplo es el funcionamiento del encéfalo, que se compara con cualquier tecnología que sea la más avanzada, impresionante y con un halo de misterio del periodo en cuestión. Así Descartes comparó el encéfalo con una máquina hidráulica; Freud con una de vapor; posteriormente se asimiló el encéfalo a una centralita telefónica, después a un circuito eléctrico, para terminar llegando al ordenador; últimamente ya se encuentran textos en los que se le asimila a un navegador web o a Internet.
Cuando imaginamos el futuro estamos presos de exactamente el mismo sesgo cognitivo. Las personas que se plantean que el universo pueda ser una simulación lo hacen basándose en lo que la realidad virtual es capaz de hacer hoy día, lo que dota de validez emocional a la comparación pero no por ello la hace más probablemente cierta.
Y es que la realidad virtual está cada vez en más sitios, desde entornos para la rehabilitación de personas que han sufrido infartos cerebrales, en videojuegos (de todo tipo), hasta simulaciones hiperrealistas que permiten el entrenamiento seguro del personal especializado que va a realizar tareas muy complejas y potencialmente muy peligrosas.
Lo que puede llegar a conseguir la realidad virtual lo ilustra la vasca Virtualware que ha sido capaz, por ejemplo, de crear una simulación para GE Hitachi Nuclear Energy en la que se puede realizar el entrenamiento realista del movimiento del combustible radiactivo de una central nuclear, una operación en la que el nivel de conocimientos exigidos y la coordinación operativa del personal es del máximo nivel, y donde cualquier discrepancia con la realidad puede salir muy cara.
Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance
El artículo Actúa localmente: simulaciones hiperrealistas se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Actúa localmente: impresión 3D de piezas aeronáuticas de titanio
- Actúa localmente: huesos a partir de ARN modificado e impresoras 3D
- Actúa localmente: convertidores de potencia basados en carburo de silicio
La feminización de las aguas, cosa de humanos
María Larumbe / GUK
Tirar de la cadena o eliminar productos por el fregadero son gestos rápidos y eficaces que nos permiten desprendernos con facilidad de los residuos que generamos. Sin embargo, ¿te has parado a pensar alguna vez dónde van a parar esos productos? La realidad es que continúan su camino hacia el mar y los ríos del entorno y, aunque sean tratados por las depuradoras, algunos contaminantes acaban llegando a los ecosistemas marinos y fluviales, provocando fenómenos de lo más sorprendentes. De hecho, malas prácticas como desechar fármacos, productos de limpieza o algunos plásticos habituales del hogar de manera inadecuada causan problemas en el equilibrio marino como, por ejemplo, el cambio de sexo de algunos peces y moluscos.
No hay que olvidar que los peces, desde su fase embrionaria y durante toda su vida hasta que mueren, se ‘beben’ todo lo que no puede ser tratado por las depuradoras como algunos compuestos químicos, que debido a su naturaleza, evitan la acción de los sistemas de depuración. Algunos de ellos, como los detergentes de tipo alquifenol etoxilado, componentes plásticos como los ftalatos, pinturas, o fármacos de distinta índole como las píldoras anticonceptivas o los antidepresivos, pueden alterar el sistema endocrino de algunas especies acuáticas, provocando cambios en el crecimiento, desarrollo, comportamiento e incluso en sus sistemas reproductor e inmunológico.
En este sentido, una de las alteraciones más llamativas es la feminización de algunos organismos acuáticos, lo que se conoce como fenómeno intersex. Se trata de un fenómeno descubierto en la década de los 90 por un grupo de investigadores de Reino Unido que detectaron cómo los testículos de los peces macho que habitaban en ríos próximos a zonas industrializadas y urbanizadas desarrollaban ovocitos, células reproductoras femeninas, por efecto de estos vertidos.
 Mugil cephalus (nombres comunes: mújol, corcón, muble, albur, muxo, llisa, lisa, lebrancho)
Mugil cephalus (nombres comunes: mújol, corcón, muble, albur, muxo, llisa, lisa, lebrancho)Posteriormente, estos efectos se han descrito en diferentes zonas del mundo, siempre en zonas urbanas e industriales. En 2007 el grupo de investigación de Biología Celular en Toxicología Ambiental (BCTA) de la UPV/EHU detectó este fenómeno por primera vez en la costa vasca en la población de mújoles (o corcones) presentes en la Reserva de la Biosfera de Urdaibai.
Un hecho que, como explica el biólogo Maren Ortiz Zarragoitia, miembro del BCTA e investigador en la Estación Marina de Plentzia (Plentziako Itsas Estazioa), “está asociado principalmente a unos contaminantes que tienen la capacidad de accionar el mecanismo dependiente de las hormonas femeninas, los estrógenos, haciendo que las gónadas, en vez de producir espermatozoides de una forma normal, comiencen a producir ovocitos”.
Entre los contaminantes que afectan a las alteraciones del sistema reproductivo de los peces se encuentran derivados de los detergentes como los alquifenoles, ftalatos, el Bisfenol A o BPA, un compuesto plástico muy hormonado que se utiliza habitualmente en la fabricación de empastes y que se trata de uno de los imitadores del estradiol, la hormona sexual femenina. Este compuesto ha sido detectado en los estuarios, muestras de agua, así como en la bilis de los peces, que los metabolizan y los acumulan. También se han encontrado restos de fármacos como el etinilestradiol, componente principal de la píldora anticonceptiva.
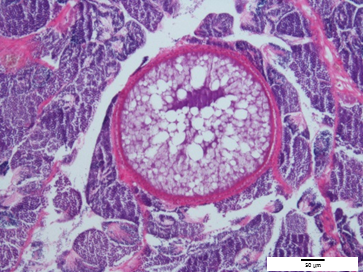 Gónadas intersex (testículos con ovocitos). Fuente: Ainara Valencia
Gónadas intersex (testículos con ovocitos). Fuente: Ainara ValenciaAdemás de la feminización de algunos machos, en el marco de sus investigaciones, estos expertos también están viendo que, en los lugares donde se ha detectado un alto porcentaje de peces intersex, los niveles de desarrollo ovocitario de las hembras no son tan buenos como en el de peces de otras zonas no contaminadas. En este sentido se han localizado hembras con ovocitos de menor calidad o con atresia -degeneración de óvulos-.
Efectos de la feminización de las aguas
 Toma de muestras. Fuente: Maren Ortiz Zarragoitia
Toma de muestras. Fuente: Maren Ortiz ZarragoitiaEn la actualidad, el BCTA está embarcado en un nuevo proyecto de investigación que se centra en la observación de la calidad de los gametos de los peces intersex con el objetivo de determinar si este fenómeno puede terminar afectando a la capacidad reproductiva de la población.
En concreto, dentro de este estudio se busca observar, por un lado, si el esperma de los machos intersex se comporta de forma similar o si tiene la misma calidad que la de los machos que no han estado expuestos a estos contaminantes y si este hecho repercute en la fertilidad de sus hembras, es decir, si sus ovocitos son de peor calidad que los de las hembras de zonas más limpias.
Las muestras de peces que se están investigando dentro de este proyecto son, sobre todo, mújoles o corcones, una especie abundante en las aguas vascas, fácil de capturar y que es muy buena para poder hacer comparativas, ya que vive tanto en zonas contaminadas como en zonas libres de estos componentes. Además de en los mubles, también se está caracterizando el fenómeno intersex en moluscos como ostras y mejillones, así como en copépodos, organismos presentes en el plancton.
Este estudio se está centrando sobre todo en Urdabai y en Pasaia, dos de las zonas con más organismos intersex detectados en Euskadi. Cuestión que, aunque resulte sorprendente en el caso de Urdaibai, declarada Reserva de la Biosfera por la UNESCO en 1984, puede estar relacionada, como explica Ortiz Zarragoitia, con la actual depuradora de aguas residuales de la zona, “que actualmente solo hace un tratamiento primario, quitando sólidos y partículas, y no evita la persistencia de los contaminantes diluidos en el agua”, así como con el aumento de la población en la zona de Gernika y alrededores. De todas formas, esperamos que con la conexión de la nueva depuradora de aguas residuales se vea una recuperación en la zona”.
Así al menos ha ocurrido en el caso de Pasaia, en donde se aprecia “una tendencia a la baja en los efectos hormonales, en comparación con años anteriores tras la instalación de la nueva depuradora de aguas residuales de Loiola”.
Hacia un futuro que no sea de “usar y tirar”
Para poder hacer frente a los efectos de la contaminación y el estrés ambiental, es importante reducir el uso de plásticos, mejorar la eficiencia de los sistemas de depuración y seguir apostando por el uso de nuevos recursos para depender menos de energías fósiles, que producen grandes cantidades de contaminantes.
Estas investigaciones ponen sobre la mesa la importancia de cuidar el medio acuático, ya que la salud de estos organismos y de los espacios donde viven, está asociada a nuestra propia salud. La contaminación y el estrés ambiental afecta tanto a la calidad del ecosistema y a estos peces y moluscos que también nos sirven de alimento. También invitan a pensárselo dos veces antes de tirar nada por el fregadero o el inodoro.
Además de miembro del BCTA e investigador de la Estación Marina de Plentzia, Maren Ortiz-Zarragoitia es coordinador del Máster Erasmus Mundus en Contaminación y Toxicología Ambientales ECT+ de la Universidad del País Vasco.
El artículo La feminización de las aguas, cosa de humanos se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:Envejecemos mejor que nuestros padres
 Foto: Heike Mintel / Unsplash
Foto: Heike Mintel / UnsplashSi tiene fotografías de familiares de hace varias décadas, les echa un vistazo y verifica la fecha en que se tomaron, se sorprenderá al comprobar que quienes aparecen en la imagen aparentan tener diez años más que los que tienen. En efecto, parecen más viejos. Y si es usted o su pareja quien, en este momento, tiene la edad que tenían quienes aparecen en la instantánea, se debatirá, perplejo, entre dos posibilidades: ¿Habrá envejecido mucho mejor que sus familiares? ¿O quizás es que la imagen que tiene de sí mismo le engaña y, en realidad, también usted ha envejecido aunque no lo quiera aceptar?
Quizás le ocurran ambas cosas a la vez, pero lo más probable es que usted y su pareja hayan envejecido menos que los familiares de la imagen a su misma edad. Esta es la conclusión a la que ha llegado el equipo de la gerontóloga Taina Rantanen de la Universidad de Jyväskylä, Finlandia, tras estudiar la condición física y cognitiva de dos grupos de personas, unas nacidas en 1910 y 1914, y las otras, cerca de tres décadas después. Las del primer grupo fueron examinadas entre 1989 y 1990, con 80 y 75 años de edad, y las del segundo grupo entre 2017 y 2018, también con 80 y 75 años de edad. A todas ellas se les hicieron pruebas de desempeño físico y de capacidad cognitiva.
Los del grupo que habían nacido tres décadas más tarde, caminaban más rápidamente y tenían más fuerza, tanto en las manos, al sujetar objetos, como en las piernas. Y en lo que se refiere a las capacidades cognitivas, los nacidos más tarde tenían más fluidez verbal, reaccionaban con mayor rapidez al realizar tareas complejas de movimiento de dedos y obtuvieron mejores resultados en ejercicios de correspondencias entre símbolos y números. En ambos casos se han comparado los registros correspondientes a personas de la misma edad.
El mejor desempeño físico y cognitivo que reflejan los resultados de las pruebas en quienes nacieron tres décadas más tarde no tuvo, no obstante, carácter general. Las medidas de función respiratoria, por ejemplo, no mostraron mejoría, ni tampoco las de la tarea de memoria a corto plazo que consiste en recordar secuencias numéricas.
Con el paso de los años, las condiciones de vida han mejorado en gran parte del mundo, y desde luego lo han hecho en los países occidentales. La prosperidad ha propiciado una mejor alimentación, con todo lo que ello implica en términos de salud. Pero también ha mejorado, y mucho, la atención médica. La gente ha estado cada vez más sana y es, por ello, lógico que llegue en mejores condiciones a edades avanzadas.
En lo que se refiere al desempeño cognitivo, un mejor estado de salud también ha podido ser un factor positivo pero, en este caso, los años de formación han ejercido una influencia determinante. De hecho, cuando se descuenta el efecto de los años de aprendizaje, las diferencias entre los grupos nacidos en épocas distintas se atenúan hasta casi desaparecer.
Por último, debe considerarse el efecto del nivel formativo sobre el estado de salud. Quienes tienen mejor formación también tienen hábitos de vida más saludables, acuden al médico con más diligencia y, dependiendo del país y la región en la que viven, tienen acceso a mejores servicios de salud. Se cierra así el círculo virtuoso que propicia un envejecimiento más saludable, una vejez más grata y una vida más prolongada. De lo que se trata es de que cada vez sean más, en todo el mundo, las personas que entran en ese círculo.
Fuentes:
Koivunen K et al: Cohort differences in maximal physical performance: a comparison of 75- and 80-year-old men and women born 28 years apart. J Gerontol A Biol Sci Med Sci, 2020 Sep 4, glaa224, doi: 10.1093/gerona/glaa224
Munukka, M eta al: Birth cohort differences in cognitive performance in 75- and 80-year-olds: a comparison of two cohorts over 28 years. Aging Clin Exp Res, 2020 Sep 12, doi: 10.1007/s40520-020-01702-0
Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU
El artículo Envejecemos mejor que nuestros padres se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- Si estás embarazada, mejor no consumas alcohol
- Una población mejor formada es una población más sana
- Nuestros ancestros asesinos
José Miguel Viñas – Naukas Bilbao 2019: Meterorología cuántica
 Foto: NOAA / Unsplash
Foto: NOAA / UnsplashLa meteorología cuántica es esa rama de la física que busca respuestas a los cuantos: ¿cuánto pesa una nube? ¿A cuánta velocidad caen las gotas de lluvia? ¿Cuántos rayos caen en la Tierra ahora mismo? Una de las características definitorias de la meteorología cuántica es que emplea unidades de medidas un poco raras, como el elefante asiático para la masa. Unos de los gurús de este campo, José Miguel Viñas, nos da algunas respuestas.
José Miguel Viñas es físico del aire y comunicador científico, meteorólogo en Meteored, en el portal www.tiempo.com, y consultor de la Organización Meteorológica Mundial.
Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus
El artículo José Miguel Viñas – Naukas Bilbao 2019: Meterorología cuántica se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- José Miguel Viñas – Naukas P4K 2019: De nubes las pinacotecas están llenas
- Naukas Bilbao 2017 – José Miguel Viñas: Me río yo del cambio climático
- José Ramón Alonso – Naukas Bilbao 2019: Son nuestros amos y nosotros sus esclavos
El colesterol de su membrana es lo que permite al VIH infectar las células
Un equipo de investigadores del Instituto Biofisika (UPV/EHU) ha descrito cómo el colesterol presente en la membrana del virus de la inmunodeficiencia humana (VIH) organiza y dirige la maquinaria viral para que el virus pueda entrar en nuestras células e infectarlas. Este hallazgo abre una nueva puerta para el desarrollo de fármacos más directos y eficientes para frenar la infección del virus.
El VIH es el virus causante del síndrome de la inmunodeficiencia adquirida (SIDA) debido a que las células que infecta y destruye son células inmunitarias. Este virus posee una membrana lipídica rica en colesterol, y precisamente este lípido es el objeto del estudio. Insertada en la membrana lipídica se encuentra la proteína de fusión o de envuelta ‘Env’, la cual a su vez está compuesta por dos subunidades, gp120 y gp41. La subunidad gp120 es la encargada de reconocer y unirse a la célula huésped mediante los receptores celulares. Una vez anclada en la célula, la subunidad gp41 sufre un cambio conformacional y se inserta en la membrana de la célula huésped, atrayéndola hacia el virus e induciendo la fusión entre ambas membranas. Esta fusión permite que el virus entre, infecte a la célula y se replique.
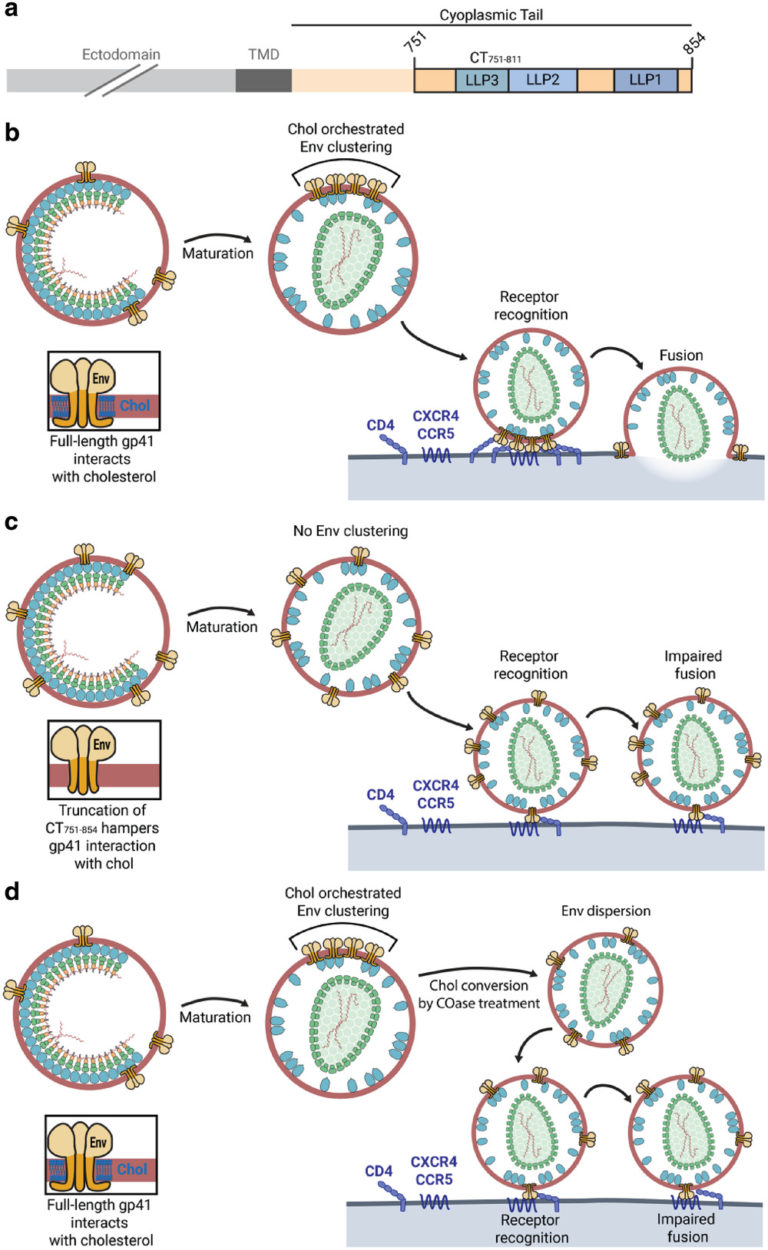
A diferencia de otros virus como el de la gripe o los diferentes coronavirus, el VIH posee muy pocas copias de proteínas ‘Env’. Para poder acceder eficientemente a la célula huésped, las proteínas ‘Env’ tienen que reorganizarse formando una agrupación o clúster. El trabajo demuestra que una región de la proteína ‘Env’ interacciona con el colesterol del virus, y que esta unión es lo que permite que ‘Env’ se reorganice en grupo y pueda infectar las células huésped de forma efectiva.
Con anterioridad a este estudio publicado por el grupo del Instituto Biofisika se conocía la composición exacta de la membrana viral y que el colesterol era un elemento importante para la estabilidad e infectividad del virus, ya que la eliminación o disminución del colesterol viral causa la pérdida de capacidad de entrar a la célula huésped. También se conocía que las proteínas ‘Env’ se reorganizaban en un solo clúster, y que además este proceso era necesario para que el virus fuera infectivo.
Sin embargo, se desconocía el papel específico del colesterol en la infectividad del virus y si estaba involucrado en la formación de clústers de ‘Env’, así como qué región de la proteína ‘Env’ era la encargada de interaccionar directamente con el colesterol. Este estudio responde a estas preguntas dilucidando el mecanismo molecular por el cual el colesterol viral y la región citoplasmática de ‘Env’ interaccionan, permitiendo que ‘Env’ forme los clústers indispensables para que el VIH sea infectivo.
El papel de los lípidos en la estructura y función de diversas proteínas es una temática muy desconocida. Esto se debe a la falta de herramientas para llevar a cabo estudios concluyentes y al hecho de que la unión de un lípido a una proteína puede ocurrir en tiempos muy cortos, del orden de milisegundos, lo cual hace que estudiar y esclarecer dichos procesos represente un desafío importante para la ciencia. En este contexto, otra de las aportaciones importantes del estudio es el desarrollo y empleo de herramientas químicas englobadas dentro de la química biológica, que permiten el estudio de procesos biológicos in vivo, así como que el estudio se ha realizado en partículas virales directamente.
Este descubrimiento podría tener efectos inmediatos en el desarrollo de fármacos que desestabilicen y bloqueen al virus, y así evitar que se propague la infección. Además, el conocimiento generado por este trabajo también tiene importantes implicaciones en el desarrollo de vacunas que bloqueen el virus antes de que se establezca la infección. ‘Env’ es la única proteína en la superficie del virus y por lo tanto la única proteína viral accesible y susceptible de generar anticuerpos que eviten la entrada del virus a la célula huésped, el primer paso de la infección. Sin embargo, hasta la fecha no se han conseguido diseñar inmunógenos capaces de generar anticuerpos neutralizantes que puedan ser usados en una vacuna, probablemente porque, entre otras cosas, no se ha conseguido imitar el inmunógeno tal y como se presenta en la infección real. Por lo tanto, el conocimiento de la estrecha relación entre ‘Env’ y colesterol generado en este trabajo podría ayudar a mejorar el diseño de inmunógenos usados para el desarrollo de vacunas.
“Además, la interacción de proteínas con colesterol también podría tener una gran relevancia en el SARS-CoV-2, el virus causante de la COVID-19. En el caso del SARS-CoV-2, parece que el colesterol en las células del paciente juega un papel importante a la hora de regular la infectividad del virus, pues si se altera el metabolismo normal del colesterol en un paciente se puede ver afectada la fuerza con la que el SARS-CoV-2 infecta a sus células. Con el abordaje y las herramientas moleculares utilizadas en el trabajo desarrollado en el Instituto Biofisika se podría estudiar a nivel molecular el papel específico del colesterol en la regulación de la infectividad del SARS-CoV-2, y así entender mejor las vías de entrada del virus y cómo bloquearlas”, comenta Lorizate.
Referencia:
Jon Ander Nieto‐Garai, Aroa Arboleya, Sara Otaegi, Jakub Chojnacki, Josefina Casas, Gemma Fabriàs, F‐Xabier Contreras, Hans‐Georg Kräusslich, y Maier Lorizate (2020) Cholesterol in the Viral Membrane is a Molecular Switch Governing HIV‐1 Env Clustering Advanced Science doi: 10.1002/advs.202003468
Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa
El artículo El colesterol de su membrana es lo que permite al VIH infectar las células se ha escrito en Cuaderno de Cultura Científica.
Entradas relacionadas:- ¿Sirve de algo la ‘pastilla del colesterol’?
- Cómo criopreservar células madre
- Cómo ver todas las células en tejido cerebral vivo

