Cuaderno de Cultura Científica

El Albert Einstein adulto nunca abrazó ninguna religión organizada. Nacido judío, abandonó las costumbres y tradiciones del judaísmo cuando tenía doce años, y nunca volvió a relacionarse con un culto establecido. Sin embargo, no sería cierto decir que Einstein no era religioso, si bien en un sentido muy concreto. Expresó a menudo agradecimiento y un profundo sobrecogimiento ante lo que él describió como “esa fuerza que está más allá de lo que podamos comprender”, la esencia según Einstein de cualquier religión.

Imagen del espacio profundo (agrupación galáctica SMACS 0723)  captada por el Telescopio Espacial James Webb en 2022. Fuente: NASA, ESA, CSA & STScI

La legislación del Imperio Alemán (el Segundo Reich) exigía que todo estudiante a partir de doce años tuviese una educación religiosa oficial, fuese esta la que fuese siempre que estuviese reconocida por el estado. Así, los padres judíos de Einstein, por lo demás nada religiosos, contrataron a un pariente lejano para educarle en su tradición. Con once años, el joven Albert abrazó el judaísmo con furia. Para sorpresa de sus padres (y quizás, disgusto) Einstein se convirtió en un judío practicante, incluso rehusando comer cerdo. Más tarde describiría esta fase como su “paraíso religioso”. Pero, la fase no duraría mucho.

A la edad de doce años, Einstein descubrió el mundo de la ciencia y las historias de la Torá que tanto había disfrutado ahora le sonaban como cuentos para niños. En un movimiento pendular, rechazó su anterior religiosidad y una visión del mundo que ahora percibía como correspondiente a un cuento de hadas. Durante el resto de su vida Einstein mantuvo esa misma opinión de la religión organizada, describiendo la creencia en un dios personal o la creencia en una vida después de la vida como muletas para supersticiosos o miedosos. No participó nunca en un ritual religioso tradicional: rehusó celebrar en un bar mitzvah (la celebración del reconocimiento como adulto desde el punto de vista de la ley judía) a los trece años, sus bodas fueron civiles, nunca acudió a un servicio religioso y eligió que su cuerpo fuese incinerado, algo expresamente contrario a la tradición judía.

Y sin embargo, Einstein se describía a sí mismo como religioso. Se cuenta la anécdota de que en una fiesta en Berlín en 1927 había un invitado que había estado haciendo comentarios sarcásticos acerca de la religión durante toda la velada. Al hombre, un crítico literario llamado Alfred Kerr, se le advirtió de que no hiciese esos comentarios delante de Einstein. Kerr fue a buscar a Einstein incapaz de creer que el gran hombre de ciencia fuese tan religioso. Einstein replicó, “Sí, puedes llamarlo así. Intenta penetrar en los secretos de la naturaleza con tus limitados medios y encontrarás que […] queda algo sutil, intangible e inexplicable. La veneración por esta fuerza que está más allá de lo que podemos comprender es mi religión. Hasta ese punto soy, de hecho, religioso”.

El sentimiento religioso cósmico

Einstein creía en algo que él llamaba “el sentimiento religioso cósmico”. Al estudiar el universo sentía que los humanos estamos intrínsecamente limitados a un conocimiento solo parcial de la naturaleza. Habría un nivel de la existencia que nunca podríamos comprender. Algo complejo, inexplicable y sutil. El sentimiento religioso cósmico se expresaba como respeto y amor por este misterio.

Como buen científico Einstein analizó esta creencia. En un artículo del 9 de noviembre de 1930 que escribió para New York Times Magazine titulado “Religión y ciencia” argumentaba que existían tres etapas en la evolución de la religión. Al comienzo, decía, la gente se enfrentaba al miedo básico ante los peligros del universo y esto llevó a la creencia de que debe haber algo poderoso cuyos caprichos marcan el destino humano. A continuación aparece la idea del dios antropomorfo que puede castigar y recompensar, lo que conduce a los conceptos de moralidad, así como a generar respuestas acerca de la vida después de la muerte. Más allá de esto, continuaba Einstein, está el sentimiento religioso cósmico, un sentimiento de la impotencia e inutilidad humanas ante la naturaleza y el “mundo del pensamiento”.

Escribió que el universo y su funcionamiento es lo que inspira este sentimiento. En este tipo de religiosidad, el practicante desea experimentar ser parte del universo en un sentido holístico del término, en contraposición a ser un individuo separado de él. Einstein citó desde los escritos de Schopenhauer hasta los Salmos de David, pasando por las escrituras budistas, como ejemplos de esta experiencia casi mística. Por último, insistió en que este sentimiento era tan universal, tan libre de dogmas, que ninguna religión en concreto lo podía abarcar y, por lo tanto, estaba intrínsecamente separado de la religión organizada. De hecho, el fin último de toda la ciencia y el arte era inspirar este sentimiento tan intenso, y fruto de él era la dedicación solitaria durante años a la ciencia de gente como Kepler o Newton. Claramente, la religión, si bien una definición muy específica de religión, era crucial en el pensamiento de Einstein.

No es de extrañar, pues, que Einstein siempre mantuviese que la ciencia y la religión se beneficiaban de su mutua asociación. En su opinión, lo mejor de la religión surgía directamente del impulso científico. Escribió: “Cuanto más avance la espiritualidad de la humanidad, más cierto me parece que el camino hacia la genuina religiosidad no pasa por el miedo a la vida, o por el miedo a la muerte, y la fe ciega, sino en esforzarse por alcanzar el conocimiento racional”. Era la búsqueda del conocimiento mismo lo que Einstein consideraba la base de la religión.

La visión habitual del público de la posición de Einstein con respecto a la religión parece indicar que esta está llena de aparentes contradicciones. Si bien Einstein siempre mantuvo este sentimiento religioso cósmico y, en este sentido, sus menciones a dios se referían a un dios próximo al de Spinoza [*], los líderes religiosos se afanaban por atraerse a Einstein, si no a su religión, si a un “marco conceptual” próximo. Así, es fácil (si uno es religioso) ver el desarrollo de la física del siglo XX como indiciario de la existencia de “lo misterioso” en lo que, de otra forma, habría sido un universo completamente determinista. Einstein negó este extremo con toda contundencia. Cuando en 1921 el Arzobispo de Canterbury le preguntó cómo afectaba la relatividad a la religión, contestó que no le afectaba. La relatividad, insistió, era totalmente científica y no tenía nada que ver con la religión.

Nota:

[*] Próximo, pero no igual. Einstein suele referirse al “orden” del universo como una de sus características más maravillosas; Spinoza afirma que el orden, cualquier orden, es una creación humana. Esta distinción hace al “dios o naturaleza” de Spinoza mucho más ilimitado que el “dios” de Einstein.

Para saber más:

Einstein y la belleza matemática
Ciencia, arte, religión
Kelvin, padre de la termodinámica: cuando la religión inspira a la ciencia
La neurociencia como religión

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

Una versión anterior de este artículo se publicó en Experientia Docet el 18 de julio de 2010.

El artículo Einstein y la religión se ha escrito en Cuaderno de Cultura Científica.

Según el informe Muerte súbita y cardioprotección de la Sociedad Española de Cardiología (SEC), cada año en España se dan en torno a 30.000 casos de muerte súbita fuera de centros sanitarios y 15.000 intentos de reanimación por parte de los servicios de emergencia. Estos fallecimientos repentinos e inesperados suelen estar provocados, en la gran mayoría de los casos, por alteraciones del ritmo cardíaco que llevan a una parada. Una actuación rápida y adecuada, en los primeros 8 minutos, resulta vital para poder salvar la vida al paciente con paro cardíaco y disminuir el riesgo de secuelas. Cada minuto que pasa sin ninguna intervención implica un 10 % menos de probabilidad de que la persona sobreviva.

Foto: Michel E / Unsplash

La reanimación cardiopulmonar (RCP) es una maniobra fundamental ante paros cardíacos y su realización adecuada duplica o incluso triplica las probabilidades de que el paciente pueda seguir viviendo. Sin embargo, solo un 30 % de los españoles sabe realizar una RCP. Los cardiólogos estiman que se podrían salvar entre 1.5000 y 3.000 vidas cada año si la población española contara con la formación necesaria para realizar esta maniobra. Según la ley, educar en la RCP debería ser obligatorio en Educación Primaria, pero la realidad es que la enseñanza de primeros auxilios en la escuela es minoritaria en nuestro país. Esto determina que, mientras que en los países nórdicos las probabilidades de supervivencia ante una parada cardíaca en la calle son del 30 %, en España estad se encuentran entre el 5 y el 10 %.

Las maniobras de reanimación cardiopulmonar han evolucionado radicalmente a lo largo de los siglos. Por ejemplo, antes del siglo XX, la técnica predominante se centraba solo en la ventilación asistida, ya fuera con un fuelle o boca a boca. Sin embargo, más adelante se observó que la supervivencia era mayor cuando se realizaban compresiones torácicas, lo que permitía que la sangre siguiera circulando. La RCP, tal como la conocemos en la actualidad, se implantó no hace mucho: en los años 60 del siglo pasado. Los médicos Kouwenhoven, Safar y Jude defendieron las insuflaciones boca a boca junto a las compresiones torácicas y esta técnica fue la que se expandió a lo largo del mundo.

La RCP sigue en constante evolución, conforme van surgiendo nuevas evidencias científicas que nos muestran qué criterios aportan una mayor supervivencia o aparecen nuevas tecnologías. Así, factores como la rapidez y el número de compresiones, la alternancia de compresiones con insuflaciones o el uso del desfibrilador son detalles que se han ido actualizando o incorporando con el tiempo.

De hecho, hace menos de 20 años se defendía que la población general debía realizar 15 compresiones torácicas por cada 2 insuflaciones seguidas. No obstante, investigaciones al respecto detectaron que era mucho más importante para la supervivencia las compresiones torácicas y esto llevó a defender que se hicieran 30 compresiones por cada 2 insuflaciones. Hace pocos años, esto volvió a cambiar. En la actualidad, se defiende que la población general sin formación en primeros auxilios debe realizar solo compresiones torácicas ante una parada cardíaca en adultos (entre 100 y 120 por minuto, más o menos al ritmo de la Macarena), porque las insuflaciones que realizan no suelen ser efectivas y, por ello, es mejor para la supervivencia que realicen exclusivamente compresiones. Eso sí, para bebés, se siguen recomendando las insuflaciones.

No es fácil recopilar pruebas científicas de calidad sobre maniobras de urgencia vital como la RCP. Esto lleva a que su mejora, aunque constante, sea lenta. Recientemente, varios estudios científicos han aportado nuevos datos que probablemente cambien la forma en la que se realiza esta maniobra entre el personal sanitario en un futuro próximo. Una RCP «refinada» mejora hasta un 50 % la supervivencia de los pacientes con parada cardíaca, atendidos fuera del hospital por los servicios de emergencia médica, en comparación con la RCP convencional. Esta novedosa maniobra se denomina RCP-ECA, que significa reanimación cardiopulmonar con elevación controlada automática de la cabeza y el tórax. 

Una de las desventajas de la RCP convencional, como explica el director médico de los Servicios de Emergencias Médicas del distrito de Dallas, Paul Pepe, es que esta no solo hace fluir la sangre hacia adelante en las arterias, sino que también provoca una presión hacia atrás en las venas. Esto implica una mayor presión intracraneal, que compromete el flujo sanguíneo en el cerebro. Para remediarlo, a la RCP convencional se añade el uso de un dispositivo que eleva de forma gradual tanto la cabeza como el tórax.

Además, también se usa un aparato, denominado dispositivo de umbral de impedancia, que se acopla a la vía aérea, en combinación con un sistema de compresión y descompresión del tórax. La función del artilugio es regular la presión del tórax durante las fases de descompresión de la RCP, al restringir de forma selectiva el flujo innecesario de aire al interior del tórax, se reduce la presión intracraneal y, con ello, mejora el flujo sanguíneo al cerebro.

En resumen, la RCP-ECA mejora el flujo sanguíneo hacia el cerebro, lo que disminuye el riesgo de daño neuronal con el paso del tiempo y aumenta de forma significativa la supervivencia. Aunque no es posible saber cuándo se extenderá su uso entre los equipos de emergencias de distintos países, los beneficios parecen claros en los ensayos clínicos con miles de pacientes. Otro ejemplo más en la constante evolución de la RCP.

Para saber más:

¿Puede un muerto regresar a la vida?

Sobre la autora: Esther Samper (Shora) es médica, doctora en Ingeniería Tisular Cardiovascular y divulgadora científica

El artículo RCP-ECA: Una nueva reanimación cardiopulmonar, para salvar más vidas se ha escrito en Cuaderno de Cultura Científica.

Michael Praetorius (1571-1621) fue el mayor académico musical de su época. Aparte de sus notables composiciones y mejoras en la práctica del bajo cifrado en el órgano, recopiló un registro enciclopédico de las prácticas musicales contemporáneas. Como musicólogo son de gran importancia sus discusiones sobre el uso de los instrumentos y las voces en los conjuntos, la afinación estándar de la época y la teoría modal, métrica y contrapuntística. Su obra Syntagma Musicum incluye en su segundo volumen un tratado de organología así como un suplemento de ilustraciones [1]. En la grabado XXI, Praetorius muestra un octeto de instrumentos de cuerdas para poder cubrir todas las voces musicales, de las más agudas a las más graves.

M. Praetorius, Syntagma musicum vol. II, figura XXI. Fuente

 

La sección de cuerda de las orquestas incluye desde el Renacimiento hasta nuestros días los conocidos cuatro instrumentos de la familia del violín (violín, viola, violonchelo y contrabajo). Es llamativo que, salvo el violín que siempre se construye siguiendo unos parámetros fijos y únicos, el resto de los instrumentos se han ido modificando múltiples veces a lo largo de la historia, y el propio tamaño de las violas, el grosor de los violonchelos o las dimensiones generales de los contrabajos no se han mantenido fijas ni tampoco bien definidas.

La nueva familia de violines Hutchins Fuente: Wikimedia Commons

El compositor Henry Brant sugirió en 1958 el diseño y construcción de una nueva y completa familia de instrumentos de violines escalados científicamente para poder cubrir de forma global y coherente todo el rango musical audible. Los investigadores Frederick Saunders y Carleen Maley Hutchins entraron de lleno en el problema y estudiaron su solución como científicos y lutieres. Después de casi ocho años de incansable trabajo, en 1965 Carleen Hutchins presentó su nuevo y completo octeto de violines. Cada miembro de la nueva familia se basa en el violín ordinario y todos comparten sus propiedades acústicas, con el objetivo de obtener sonido homogéneo en todos los rangos musicales. Todos los instrumentos de Hutchins incorporan un carácter tonal más rico y se basan en parte en las ideas presentadas por Michael Praetorius.

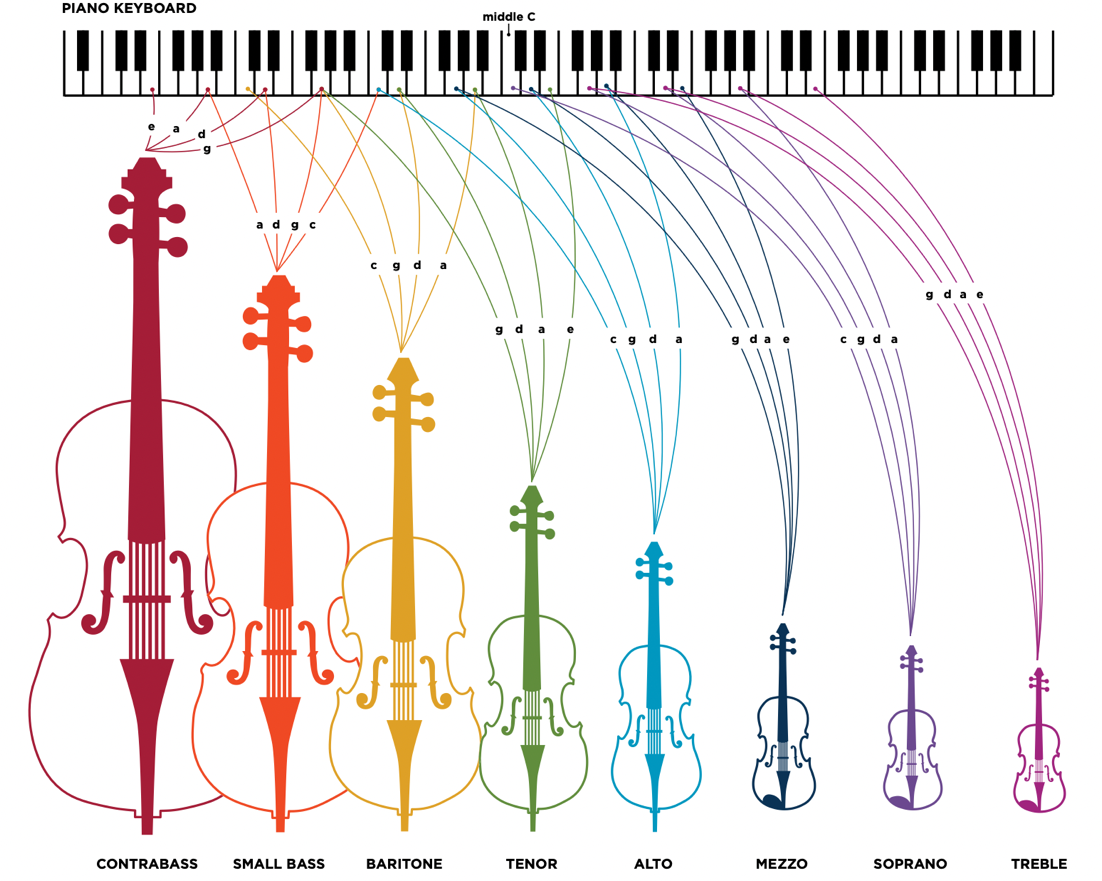La Nueva Familia de Violines creada por Carleen Maley Hutchins en 1965. Fuente

 

A diferencia de los cuatro instrumentos de cuerda estándar, la caja de resonancia de cada nuevo instrumento se construye de modo escalable dependiendo de su rango de frecuencias de funcionamiento. Así, la resonancia de aire y la principal del cuerpo de cada instrumento del octeto de violines están, respectivamente, en un tono cercano a las dos cuerdas centrales de cada violín, lo cual confiere a los nuevos instrumentos un sonido mucho más claro y equilibrado.

Análisis modal de la nueva generación

El Violín Mezzo de la nueva familia coincide con el violín ordinario creado por los clásicos lutieres de Cremona. Las 4 cuerdas de un violín se afinan a intervalos de quintas (frecuencias crecientes con factor aproximado 3/2). En el moderno temperamento igual, ello da lugar a que las cuerdas libres suenen a frecuencias Sol3=196.0 Hz; Re4=293.7 Hz; La4=440.0 Hz; Mi5=659.3 Hz (G D A E en terminología anglosajona).

Si observamos los modos de vibración medidos en el cuerpo del famoso violín “Leonora Jackson” de Antonio Stradivari (1714) encontramos que la primera resonancia de aire (A0) de este instrumento se encuentra en el rango 270-280 Hz, muy cerca de la cuerda central Re4=293.7 Hz. Asimismo, encontramos que la primera resonancia de madera (CBR) se encuentra en el rango 390-400 Hz, también cerca de la otra cuerda central La4=440 Hz.

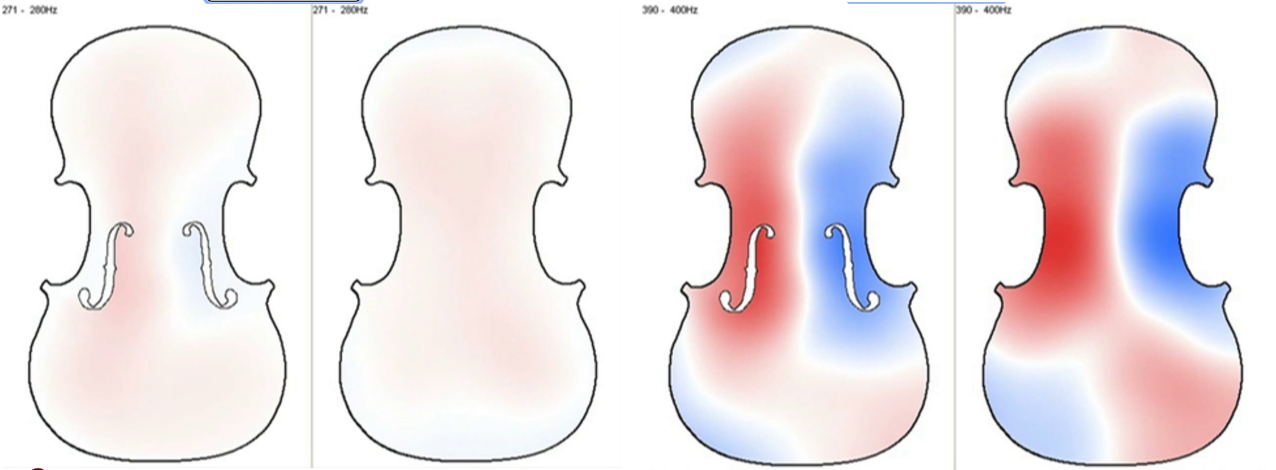Primeras resonancias y vibraciones asociadas de la caja del “Jackson” Stradivarius: A0 (270-280Hz) y CBR (390-400Hz). Fuente

Notemos que el diapasón de la nota La4 en la época barroca se afinaba en torno aproximado de 415 Hz (en lugar de los actuales 440-442 Hz de las orquestas modernas). Así pues, las dos cuerdas centrales de los violines históricos de Cremona se afinaban con un Re4=277.0 Hz y un La4=415.0 Hz, respectivamente. Esto indica que las resonancias del aire y madera medidas en el “Jackson” Strad 1714, se encuentran aún más cerca de las frecuencias vibratorias de las dos cuerdas libres centrales del violín.

Carleen Hutchins ajustó todas las cajas de resonancia de su octeto a las frecuencias de las cuerdas centrales y escaló todos los instrumentos de forma coherente y brillante. Aunque la tradición e historia musical clásica siempre ha evolucionado lentamente, la innovadora nueva familia de violines creada por Carleen Hutchins supuso un importante hito en lutería y acústica musical, e influyó a múltiples científicos, constructores de instrumentos, e importantes músicos. Como simple ejemplo histórico de estos hechos, podemos citar al director de orquesta Leopold Stokowski , el violonchelista Yo-Yo Ma o a la organización musical The Hutchins Consort, que desarrolla en este ámbito su importante actividad docente, investigadora y cultural.

Referencias

[1] Michael Praetorius (1620) Syntagma musicum vol. II. Suplemento ilustrado Theatrum Instrumentorum

[2] Quincy Whitney (2020) American luthier: the art and science of Carleen Hutchins. Acoustics Today, vol 16, n.1, pp. 10-19.

El artículo La nueva familia de violines de Carleen Maley Hutchins se ha escrito en Cuaderno de Cultura Científica.

Foto: Tim Marshall / Unsplash

El pasado 21 de septiembre se impartió la conferencia «Historia de una ola» en la Biblioteca Bidebarrieta dentro del ciclo Bidebarrieta Científica, en el marco de Bilbo Zientzia Plaza.

La física Maia García Vergniory y el surfista Kepa Acero explican en esta charla por qué unas olas se abren y otras se cierran, por qué algunas veces vienen en serie y otras no, o qué papel juegan las mareas, el viento y el fondo marino en las olas que surfeamos. De hecho, cada vez que alguien que practica surf mira las tablas de predicción está analizando fenómenos físicos, y en esta charla se demuestra que para tener una actitud científica no hace falta ser profesional de la ciencia.

Maia García Vergniory es investigadora principal en el Instituto Max Planck de Fisicoquímica de Sólidos en Dresde (Alemania). Maia ha sido elegida muy recientemente como APS Fellow de la American Physical Society por sus contribuciones al descubrimiento de la química cuántica topológica. Kepa Acero es surfista profesional y documentalista, conocido por documentar sus viajes en solitario en busca de las olas más aisladas del planeta.

Edición realizada por César Tomé López

El artículo Maia García Vergniory y Kepa Acero – Historia de una ola se ha escrito en Cuaderno de Cultura Científica.

Foto: Aarón Blanco Tejedor / Unsplash

Hay pocas cosas tan necesarias y al mismo tiempo tan indeseables como el dolor. Nos advierte y defiende de algo que nos perjudica o nos puede perjudicar. Hay dolores nociceptivos, debidos a estímulos dañinos; psicógenos, con gran componente emocional; e incluso neuropáticos, cuando el daño lo sufre el propio sistema nervioso. Hay dolores que solo pasan y dolores que se quedan, como el crónico, aquel que dura más de tres meses y puede vincularse a cuadros de ansiedad, depresión e incluso al suicidio.

Acabar con el dolor y aliviar al que lo sufre es un acto de humanidad encomendado a la ciencia y a los profesionales sanitarios, y los fármacos analgésicos disponibles actualmente ayudan al paciente a vivir con mejor calidad de vida. Incluyen antiinflamatorios no esteroideos como el ibuprofeno, opioides menores como la codeína y opioides mayores como la morfina, el fentanilo y la oxicodona.

En los últimos años, la prescripción de opioides ha crecido considerablemente debido a que ha disminuido el miedo a su uso. Sin embargo, a pesar de su eficacia, su empleo prolongado no está exento de problemas, por lo que la búsqueda de alternativas resulta de gran interés.

Limitaciones de los analgésicos actuales

El consumo crónico de opioides produce, entre otros problemas, la aparición de tolerancia –una necesidad de mayor dosis para lograr el efecto deseado– y cuadros de adicción. De modo que ciertos pacientes que comienzan a tomarlos pueden terminar abusando de ellos.

Y a pesar de los perjuicios que generan los opioides, no se ha encontrado nada mejor para el tratamiento del dolor moderado y severo. De hecho, tan malo es sobretratar como infratratar con ellos. La clave está en realizar un uso racional de los mismos ayudando al paciente a aliviar su malestar, pero vigilando los problemas derivados de su consumo crónico.

La OMS aboga por un tratamiento escalonado que consiste en añadir opioides menores o mayores solo cuando los antiinflamatorios no esteroideos, considerados más seguros, sean insuficientes.

No obstante, la utilización de estos últimos tampoco está exenta de efectos perniciosos, sobre todo cuando se consumen dosis altas y de forma crónica. Su empleo prolongado podría producir problemas gastrointestinales y renales.

¿Es posible separar los efectos terapéuticos de los adversos?

La mayoría de los medicamentos funcionan gracias a la interacción con macromoléculas presentes en nuestro organismo, a las que denominamos dianas farmacológicas. Fruto de esta interacción fármaco-diana, se altera la función de esas macromoléculas, lo que da lugar a eventos bioquímicos y fisiológicos conocidos como efectos farmacológicos. Algunos son de carácter terapéutico y otros, adversos.

Los antiinflamatorios no esteroideos y los opioides reducen el dolor a través de la interacción con dos dianas concretas, denominadas enzimas ciclooxigenasas y el receptor opioide µ, respectivamente. El problema es que dichas dianas participan también en numerosas funciones fisiológicas en el sistema gastrointestinal, los riñones o el cerebro. Así, al actuar sobre esos compuestos, los fármacos pueden producir también daños colaterales.

Esto nos lleva a la conclusión, un tanto pesimista, de que los efectos terapéuticos difícilmente podrán separarse de los adversos: el riesgo de daño renal, gastrointestinal, tolerancia, adicción e incluso depresión respiratoria, serán peajes a pagar por el uso de analgésicos. No obstante, prometedoras herramientas como los llamados moduladores alostéricos y agonistas sesgados –que explicaremos más adelante– o la combinación de varios fármacos abren la puerta a la esperanza.

¿Qué nuevos tratamientos se están investigando?

La adenosina es una sustancia muy interesante para quienes buscan nuevas armas contra el dolor. Producida por nuestro organismo, tiene propiedades analgésicas cuando actúa sobre la diana denominada receptor de adenosina 1 (A1). Por ello, en el caso del dolor neuropático –resistente a los opioides– se han probado fármacos agonistas (activadores) del receptor A1.

Estos compuestos alivian efectivamente el dolor pero, al actuar también sobre el A1 presente en el corazón, pueden reducir la frecuencia cardíaca. Ante este problema, los farmacólogos han recurrido a un modulador alostérico del receptor A1.

En este caso, los moduladores alostéricos son fármacos que se unen al receptor A1 en un punto diferente al que lo hace la propia adenosina. Pueden ser positivos y negativos en función de si colaboran o no con ella. Así, actuando de manera cooperativa junto a la adenosina presente en el tejido dañado, los moduladores alostéricos positivos potencian su acción contra el dolor.

Los agonistas sesgados son otras herramientas esperanzadoras ya que, al unirse a un receptor diana, pueden activar ciertas funciones de manera más eficiente que otras. Esta capacidad haría realidad el objetivo de producir solo efectos terapéuticos, sin los adversos.

Recientemente, se ha hallado un agonista sesgado del receptor A1 que activa preferentemente ciertas vías celulares, aliviando el dolor sin provocar depresión cardiorrespiratoria. También se han encontrado agonistas sesgados que al actuar sobre otra diana, denominada adrenoceptor α2A, producen analgesia sin el efecto sedante que limita a otros fármacos que actúan sobre dicha diana.

Y tendríamos, por último, la estrategia de asociar opioides y compuestos con efecto analgésico para reducir la dosis de los primeros y evitar así sus efectos perniciosos. Un ejemplo sería la combinación con el cannabis medicinal.

Aunque de manera prudente, podemos decir que avanzamos en el descubrimiento de nuevos tratamientos analgésicos eficaces que mejorarían el perfil de seguridad del arsenal existente. Sabemos que el camino es largo, pero el trabajo cooperativo, como el que realizan ciertos fármacos, nos llevará a nuestra meta.

Sobre las autoras: Guadalupe Rivero Calera y Aitziber Mendiguren Ordorica son profesoras agregadas del Departamento de Farmacología en la Facultad de Medicina y Enfermería de la Universidad del País Vasco / Euskal Herriko Unibertsitatea

Este artículo fue publicado originalmente en The Conversation. Artículo original.

El artículo ¿Es posible acabar con el dolor sin efectos adversos? se ha escrito en Cuaderno de Cultura Científica.

Podemos empezar con Wikipedia: el vendaje neuromuscular o kinesiotaping son unas cintas de algodón con un adhesivo acrílico, de diferentes y espectaculares colores (rojo, amarillo, azul, negro, beige, …), que se utilizan para tratar lesiones en atletas y en otros trastornos físicos. En los profesionales, se pueden colocar en la zona lumbar, hombros, rodillas, cuello o espalda.

Fuente: Wikimedia Commons

Fue un invento de Joseph Komp, de Bowling Green, en Kentucky, y la patente, con el título “Adhesive Tape Products”, está fechada el 11 de agosto de 1970. La técnica fue utilizada en los años 70 en el Japón por muchos especialistas en ortopedia así como en quiropráctica y acupuntura. Más adelante, se hizo popular entre atletas y olímpicos japoneses. Difundió su uso el quiropráctico japonés Kenzo Kase y llegó a muchos ciudadanos cuando, para las Olimpíadas de Pekín de 2008, se donó para su uso a atletas de 58 países.

Las vendas utilizadas son finas, elásticas y de algodón. Pueden estirarse hasta un 130%-140% de su longitud. Si la venda se aplica en un paciente con un estiramiento muscular excesivo, la venda también se alargará y creará una fuerza contraria para volver a la longitud original. Esta reacción ayudará al músculo a recuperar la situación original. Esta elasticidad permite movimientos musculares más amplios pues ayuda a la recuperación. Además, funcionan durante bastante tiempo y se puede demorar la aplicación de nuevas vendas.

Llevan las vendas un adhesivo acrílico que ayuda a la sujeción y que se evapora con el calor. Se secan rápido y el uso puede llegar hasta los cuatro días. Los beneficios que se ofrecen son facilitar el movimiento muscular, reducir la fatiga muscular, quitar agujetas, inhibir el dolor y recuperar por reducción de la hinchazón o edema y ayudar al flujo sanguíneo. Incluso se relaciona su eficacia con su color pues según cuál sea absorbe más o menos luz con aumento de la temperatura. Por ejemplo, para las lesiones musculares crónicas lo más adecuado son las cintas rojas, con mayor absorción de luz, más aumento de la temperatura y más calor para el músculo lesionado.

Pese a su extendido uso en atletas y profesionales del deporte, el kinesiotaping no ha logrado demostrar eficacia en su uso cuando se ha intentado confirmar en ensayos clínicos con una metodología aceptable en publicaciones científicas con el sistema habitual de revisión por otros científicos. Como afirma Lara Tardón en El Mundo “al contrario de lo que prometen, las kinesio tape ni mejoran la función muscular ni favorecen su recuperación, ni previenen lesiones ni tampoco las tratan. Los expertos lo tienen claro: no hay evidencia científica que demuestre ninguna de estas ventajas publicitarias”. Quizá tengan alguna eficacia pero, por ahora, no se ha conseguido demostrar en la práctica clínica y científica.

Un meta-análisis de 10 estudios elegidos por su metodología adecuada entre un total de 97, resulta que el alivio del dolor es muy bajo y ninguno de los artículos encuentra resultados de importancia clínica, según concluyen Sean Williams y sus colegas de la Universidad Tecnológica de Auckland, en Nueva Zelanda. Este vendaje puede tener un pequeño papel beneficioso en la mejora de la fuerza, el rango de movimiento en ciertos grupos de lesiones y en el error de detección de fuerza en comparación con otras cintas, pero se necesitan más estudios para confirmar estos hallazgos. La cantidad de noticias de casos y el apoyo más bien anecdótico debe garantizar una investigación experimental bien diseñada, particularmente relacionada con lesiones deportivas, para que se tenga seguridad de que es una técnica beneficiosa para los atletas.

El artículo del grupo de Rafael Muñoz López, del Hospital Universitario Reina Sofía de Córdoba, revisa la función y el uso de las vendas kinesiotaping. Después de analizar los estudios publicados hasta 2016 para resolver lesiones en el hombro, el codo, la zona dorsolumbar, cuello, pie y tobillo, y rodilla, los autores concluyen que el kinesiotaping es una técnica muy popular en los medios de comunicación y para los deportistas de élite con una gran inversión en márketing en su apoyo. Pero los estudios publicados no demuestran un beneficio claro derivado de su uso y se podría cuestionar su utilización.

Otro estudio que se puede mencionar es el firmado por Mark Thelen y sus colegas del Hospital Comunitario Winn del Ejército en Fort Douglas, Georgia, con 42 diagnosticados con tendinitis en el hombro y asignados a dos grupos, uno con el vendaje neuromuscular y el otro con vendaje simulado. En total, cada voluntario utilizó la venda en dos intervalos de tres días y se les entrevistó sobre el dolor en el hombro y los cambios en la discapacidad. Los resultados indican que nos hay disminución de dolor o de la sensación de discapacidad en los voluntarios.

En 2009, el grupo de Javier González Iglesias, del Centro de Fisioterapia Integral de Candas, en Asturias, publicó un estudio con 41 voluntarios, con 21 mujeres, que sufrían dolor en el cuello por latigazo cervical. Formaron dos grupos, uno de ellos con aplicación de la venda neuromuscular y, el segundo grupo, con el vendaje simulado. Se tomaron datos del dolor en una escala de 1 a 11, y de los movimientos del cuello, antes de iniciar la prueba, inmediatamente después de la aplicación de la venda y 24 horas más tarde.

Los voluntarios mostraron mejoras estadísticamente significativas inmediatamente después de la aplicación de la venda y en el seguimiento de 24 horas. Sin embargo, la disminución del dolor y el aumento del rango de movimiento cervical fueron pequeños y pueden no ser clínicamente significativos.

Sorpresa, el color del kinesiotaping no tiene efecto Fuente: Wikimedia Commons

Es interesante repasar algunos resultados de estudios relacionados con la distinta eficacia de los colores de las vendas en el alivio de lesiones musculares que antes he mencionado. Ashcan Çaglar y su equipo, de la Universidad Baskent de Ankara, en Turquía, lo han ensayado en 50 mujeres diagnosticadas con lesiones en el músculo trapecio en el hombro. Las pacientes tienen un edad media de 20.8 años. Utilizaron vendas de cinco colores: rojo, azul, negro, beige y blanco. Y se encuestó a las pacientes sobre cómo se sentían después de cada cinta con diferente color. La escala era de ningún calor, cálido, frío, fuerte, fresco, …

Por ejemplo, con la cinta roja el 30% no notó cambios o el 26% sintió calidez; con la cinta azul, el 32% apreció calidez y el 24% nada; con la venda negra, el 24% nada y el 22% calidez; para la cinta beige, el 26% calidez y el 20% nada; y para la venda blanca, el 34% calidez y el 20% nada. En conclusión, el color no cambia de manera significativa las percepciones de las pacientes. Quizá, como mucho, las percepciones diferentes de los colores de la venda provoque algún tipo de efecto placebo.

Resultados parecidos obtienen en su investigación sobre el color de la venda que han publicado Rocco Cavaleri y sus colegas de la Universidad de Sídney Occidental, en Australia. Participan 32 participantes sanos con 16 mujeres y edad media de 24 años. Se dividen, al azar, en cinco grupos: el primero es el control y no se le coloca venda de kinesiotaping en el muslo desde la rodilla a la cadera; los otros cuatro grupos llevan una venda beige puesta con tensión y sin tensión, y vendas rojo y azul con tensión.

Los resultados muestran que la venda no tiene un impacto beneficioso en la función de la pierna o en la fuerza de la rodilla. Y el color de la venda no influye en el rendimiento atlético de los voluntarios.

Para terminar, es interesante conocer la opinión sobre la utilización de kinesiotaping en los profesionales de la salud de Estados Unidos. Scott Cheatham y sus colegas, de la Universidad Estatal de California Dominguez Hills, redactaron una encuesta con 30 preguntas que enviaron, por correo electrónico, a 51000 profesionales de la Asociación Nacional de Entrenadores de Atletismo, la Academia de Fisioterapia Ortopédica y la Academia de Fisioterapia Deportiva. Respondieron 1083 encuestados.

La mayoría, hasta el 74%, utilizaban las vendas neuromusculares para los tratamientos posteriores a una lesión, y para controlar el dolor, hasta el 67%. El 77% consideraba que así mejoran la recepción de estímulos en la piel, y el 69% que promueve la circulación local. Sin embargo, el 40% cree que solo provocan un efecto placebo y, por ello, el 58% las usan con fines terapéuticos para aliviar dolencias. El tiempo de uso es de dos a tres días para el 60% de los profesionales aunque el 81% indica que el tiempo máximo está entre dos y cinco días.

Y, como veíamos, el 70% prefiere la venda negra y el 66% la de color beige.

Los autores concluyen que los profesionales utilizan las vendas como placebo en casi el 60% de los encuestados. Los profesionales también creen que proporciona numerosos efectos terapéuticos positivos para los usuarios, pero que se sabe poco sobre cómo se producen las mejoras. Los resultados contradictorios de los estudios pueden deberse a dos problemas principales: la fabricación y el tipo de la cinta y las variantes en los métodos de prueba y estudio.

Como apéndice curioso por los resultados, es interesante la revisión de Yu Qin y sus colegas, de la Universidad de Lanzhou, en China, sobre las publicaciones entre 2011 y 2020 que tratan de kinesiotaping. En total encuentran 677 artículos, con la mayoría publicados en Turquía, en la Universidad Hacettepe de Ankara y con la autora con más textos, Gul Baltaci, del Hospital Güven también en Ankara. El número publicaciones muestra una tendencia ascendente.

Referencias:

Çaglar, A.et al. 2016. Are the kinesio tape colors effective for patient perception? A randomized single blind trial. Journal of Exercise Therapy and Rehabilitation 3: 96-101.

Cavaleri, R. et al. 2018. The influence of kinesiology tape colour on performance and corticomotor activity in healthy adults: a randomized crossover controlled trial. BMC Sports Science, Medicine and Rehabilitation 10: 17.

Cheatham, S.W. et al. 2021. Kinesiology tape: A descriptive survey of healthcare professionals in the United States. International Journal of Sports Physical Therapy 16: 778-796.

González-Iglesias, J. et al. 2009. Short-term effects of cervical kinesio taping on pain and cervical range of motion in patients with acute whiplash injury: A randomized clinical trial. Journal of Orthopaedic & Sports Physical Therapy 39: 515-521.

Muñoz López, R. et al. 2016. Kinesiotaping. Evidencia actual. Revista de la Sociedad Andaluza de Traumatología y Ortopedia 33: 23-29.

Qin, T. et al. 2022. Research hotspots and trends of kinesio taping from 2011 to 2020: a bibliometric analysis. Environmental Science and Pollution Research DOI: 10.1007/s11356-022-22300-9

Tardón, L. 2018. Sin rastro científico que avale el “kinesiotaping”. El Mundo 7 agosto.

Thelen, M.D. et al. 2008. The clinical efficacy of kinesio tape for shoulder pain: A randomized, double-blinded, clinical trial. Journal of Orthopaedic & Sports Physical Therapy 38: 389-395.

Wikipedia. 2021. Vendaje neuromuscular. 14 agosto.

Wikipedia. 2022. Elastic therapeutic tape. 24 September.

Williams, S. et al. 2012. Kinesiotaping in treatment and prevention of sports injuries. Sports Medicine 42: 153-164.

Sobre el autor: Eduardo Angulo es doctor en biología, profesor de biología celular de la UPV/EHU retirado y divulgador científico. Ha publicado varios libros y es autor de La biología estupenda.

El artículo Desmitificando: “Kinesiotaping” o vendaje neuromuscular se ha escrito en Cuaderno de Cultura Científica.

Un tema con cierta popularidad dentro de la cultura matemática son los denominados “grandes números”. Normalmente, bajo la nomenclatura de “grandes números” se incluyen números más grandes de lo que es habitual utilizar en la vida cotidiana, en el día a día. La verdad es que es un concepto un poco ambiguo, pero tampoco hace falta que seamos muy estrictos con la definición para realizar un pequeño paseo sobre el tema.

La Enciclopedia Británica dice que hablamos de grandes números cuando son cantidades mayores que un millón, y que de manera normal suelen escribirse en forma de potencia. Un clásico, que además es fuente de muchos errores, es el billón, que en la notación de exponentes sería 1012, es decir, un 1 seguido de 12 ceros (1.000.000.000.000). Un millón de millones. La confusión relacionada con el billón está en el hecho de que en inglés (*) un “billón” son “mil millones”, es decir, 109 (1.000.000.000). Por este motivo, en ocasiones se dan noticias que son traducciones de noticias de países de habla inglesa y se utiliza, incorrectamente, el billón, cuando debería utilizarse el millardo, que es nuestra palabra para los mil millones.

Por ejemplo, en el libro Disparates y gazapos matemáticos, de Jose María Sorando, publicado por la editorial Catarata, se cita el siguiente ejemplo. En cierta ocasión en La Sexta Noticias se decía lo siguiente:

“[Madonna] Está considerada la artista más rica de la historia de la música. La reina del pop tiene una fortuna estimada entre 800 millones y un billón de euros. ¡Sí, con b!”.

La noticia quería transmitir la idea de que la artista tenía entre 800 y 1.000 millones de euros, pero la horquilla se les disparó al utilizar el término billón, que aparecía en la noticia en inglés, ya que expresaba que la artista tenía entre 800 y un millón de millones de euros.

El billete más grande que se haya emitido nunca ha sido del pengö húngaro. En 1946 el Banco Nacional de Hungría puso en circulación un billete de 100 trillones, es decir, 1020 = 100.000.000.000.000.000.000 de pengö húngaros. Véase la entrada Ceros, ceros, ceros

 

Aprovechando que hablamos de millardos (109) y billones (1012), que son dos números que todos conocemos, podemos realizar un pequeño experimento que nos permita reflexionar sobre hasta qué punto somos conscientes del valor de los grandes números. Este experimento lo leí hace años en el libro El universo y la taza de té, de la divulgadora científica K. C. Cole.

Para empezar, recordemos que en matemáticas se suelen representar los números en una línea, que puede ser abierta o cerrada. En este último caso, se coloca el número más pequeño que se quiere representar (por ejemplo, el cero) a la izquierda, mientras que el número más grande se representa a la derecha y el segmento entre ambos extremos (números) se divide de forma que se representen linealmente todos los números entre esos dos números extremos. Por ejemplo, si tomamos el segmento con extremos 0 y 10, como en la siguiente imagen, tendremos los números 1, 2, 3, 4, 5, 6, 7, 8 y 9 entre ellos, igualmente espaciados.

Hay que tener en cuenta que en la recta de los números no solo se representan los números naturales, sino todos los números reales entre 0 y 10, aunque esta cuestión no es algo importante para nuestro experimento de esta entrada.

Pero vayamos con el experimento. Tomamos una hoja de papel y la colocamos en horizontal. Esto es para que tengamos más longitud para pintar una línea horizontal y esto precisamente lo que hacemos a continuación, pintar un segmento que vaya de un extremo a otro de nuestra hoja. De manera que en el extremo izquierdo colocamos el cero (0) y en el extremo derecho el billón (1012), como aparece en la imagen.

El experimento consiste en que marquéis con un segmento vertical el lugar en el que estará representado, en la línea de los números, el millardo (109). La idea es que realicéis esta primera parte del experimento de forma intuitiva, sin pensar mucho en ello. Os animo a que antes de seguir leyendo realicéis esta primera parte, para poder reflexionar sobre el resultado.

Entonces, viene la segunda parte del experimento, que consiste en reflexionar con tranquilidad dónde estará situada la marca del millardo en la línea de los números. Para ello vamos a dividir nuestro segmento en diez partes iguales, cada una de las cuales se va a corresponder con la décima parte del billón que representa la recta, luego 100.000.000.000 (cien mil millones). Por lo tanto, las marcas entre cero (0) y un billón (1012), igualmente espaciadas, serán las posiciones de los números 100.000.000.000, 200.000.000.000, 300.000.000.000, …, 900.000.000.000, como se ve en la imagen.

Ahora, dividiremos la parte del segmento entre 0 y 100.000.000.000 (que es la primera marca de la izquierda después del cero), en diez partes iguales, cada una de las cuales se va a corresponder con la décima parte de 100.000.000.000 que representa ese trozo de segmento, luego 10.000.000.000 (diez mil millones). Por lo tanto, las marcas ahora entre cero (0) y cien mil millones (100.000.000.000), igualmente espaciadas, serán las posiciones de los números 10.000.000.000, 20.000.000.000, 30.000.000.000, …, 90.000.000.000.

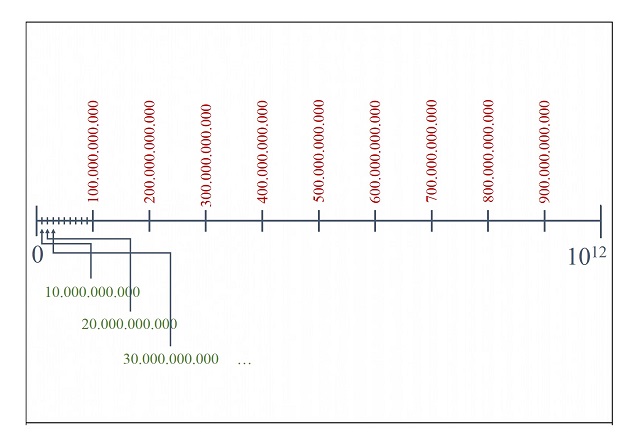
Pero nosotros estamos buscando representar el millardo (1.000.000.000), que es más pequeño aún que el número de la primera marca, que es 10.000.000.000. Por lo tanto, por último, tendríamos que dividir la parte del segmento entre 0 y 10.000.000.000 (que es esa primera marca de la izquierda después del cero, que acabamos de introducir), en diez partes iguales, cada una de las cuales se va a corresponder con la décima parte de 10.000.000.000 que representa ese trozo de segmento, luego 1.000.000.000 (mil millones). Ahora, como antes, pintaríamos las marcas entre cero (0) y diez mil millones (10.000.000.000), igualmente espaciadas, y la primera de ellas sería la que se corresponde con el número 1.000.000.000 (mil millones, el millardo), que es el que estábamos buscando representar. Aunque esta última parte no la hemos representado, ya que no tenemos espacio para las marcas, resulta evidente que el millardo, que sería la primera de esas marcas, está al lado del cero, pegadito al 0. Es decir, un millardo (mil millones) es prácticamente cero comparado con el billón (un millón de millones).

¿Dónde lo habíais colocado inicialmente? Es muy típico que, si no pensamos mucho en ello, lo coloquemos de la mitad del segmento inicial hacia la derecha, muy lejos de donde realmente está. Eso es porque pensamos más en el exponente, 9 frente a 12 (la cantidad de ceros) de su representación, que en el valor del número.

Otro billete muy grande fue el billete de 100 billones de dólares zimbabuenses, aunque, como se ve en la imagen, dice “One hundred trillion dollars”, es decir, cien trillones de dólares. De nuevo, está haciendo referencia a la expresión en inglés (*) del “trillón” que se corresponde con el número 1.000.000.000.000 que para nosotros no es más que un billón, un millón de millones

 

Volviendo a los grandes números, la verdad es que podemos sacar ejemplos de ellos, no solo en matemáticas, como haremos más adelante, sino en otros ámbitos de la vida y la cultura.

Por ejemplo, la cantidad de plaquetas de nuestro cuerpo es aproximadamente 1,8 billones, es decir, 1,8 x 1012 (resulta que el cuerpo humano tiene entre 4,5 y 6 litros de sangre, que hay 300.000 plaquetas por milímetro cúbico y que cada litro contiene 1.000.000, un millón, de milímetros cúbicos, luego de ahí nos sale que hay del orden de 1,8 billones de plaquetas en nuestro cuerpo). Pero podríamos seguir. La cantidad de células en el cuerpo humano es de 37 billones, es decir, 37 x 1012, la cantidad de configuraciones del cubo de Rubik es, aproximadamente, de 43 trillones, es decir, 43 x 1018 o el número de estrellas en el universo (observable) se estima que es alrededor de un cuatrillón, es decir, 1024.

Pero también podemos mirar a la literatura. Uno de los poemas más famosos del poeta francés Paul Fort (1872-1960) es Un corro alrededor del mundo (1913), que es un llamamiento a la amistad mundial y que dice así:

Si todas las muchachas del mundo quisieran darse la mano,
podrían hacer un corro todo alrededor del mar.
Si todos los muchachos del mundo quisieran ser marineros,
harían con sus barcas un hermoso puente sobre las olas.
Se podría hacer un corro alrededor del mundo,
si toda la gente del mundo quisiera darse la mano.

Quedémonos con esta última parte “si toda la gente del mundo quisiera darse la mano se podría hacer un corro que diese la vuelta al mundo”. Aunque la población mundial hoy en día es muy superior, en la época en la que se escribió este poema había unos dos mil millones de habitantes (2.000.000.000) y el perímetro de la Tierra es, alrededor del ecuador, de 40.075 kilómetros. Por lo tanto, si todas las personas de nuestro planeta, en aquel momento, se hubiesen dado la mano, y asumiendo que cada una de las personas representa un eslabón de 1 metro, que estirados sería aún más, tendríamos una cadena de personas de 2 mil millones de metros, luego que podría rodear casi 50 veces la Tierra.

Teniendo en cuenta que en la actualidad la población mundial es de 8 mil millones de personas, podríamos formar un corro que diese la vuelta a la Tierra, por el ecuador, 200 veces.

Imagen de la Tierra vista desde el espacio. Imagen de la National Oceanic and Atmospheric Administration, NOAA, de Estados Unidos y NASA.

 

Si miramos al mundo del arte también tenemos algunos ejemplos curiosos. Recientemente, he estado estudiando la obra de un artista abstracto eslovaco, Viktor Hulik (1949), por su relación con algunas cuestiones matemáticas, en concreto, obras como Variaciones con triángulos (2014) están creadas con sencillas estructuras cuadradas divididas en dos triángulos por la diagonal, lo que se conoce como la baldosa de Truchet (podéis leer sobre ella en las entradas del Cuaderno de Cultura Científica: Los embaldosados de Truchet y el puzle del diamante y El arte de la sencilla baldosa de Truchet).

Pero volviendo a esta obra de Viktor Hulik, está compuesta de 12 lienzos cuadrados, que en cada exposición coloca de forma aleatoria, formando una estructura rectangular 3 x 4. Por una parte, cada uno de los 12 lienzos es una estructura reticular cuadrada 8 x 8, formada por 64 baldosas de Truchet de alguno de los tres pares de colores siguientes, blanco y gris; blanco y negro; gris y negro. Por lo tanto, existen (4 + 4 + 4)64 = 1264 estructuras posibles (más de mil ciento sesenta y ocho undecillones) para esos lienzos.

Por otro lado, como en cada exposición el artista eslovaco coloca de forma distinta esos 12 lienzos formando una estructura 3 x 4, en cada exposición se ve, realmente, una obra distinta. La cuestión es que podemos calcular matemáticamente de cuántas formas distintas se pueden colocar los 12 lienzos de la obra de Viktor Hulik, en concreto, son (412) x (12!) = 8.036.313.307.545.600, más de 8 mil billones, de formas distintas de colocarlos. Si cada minuto se realizase una nueva disposición, y distinta a las anteriores, de los 12 lienzos de la obra Variaciones con triángulos, se tardarían 15 mil millones de años en mostrar todas las estructuras posibles de esa obra, lo que es más que la edad del universo, ya que según la cosmología la edad del universo, desde el Big Bang, sería de unos 13.787 millones de años.

El artista eslovaco Viktor Hulik (1949) junto a su obra Variaciones con triángulos (2014) en la exposición Viktor Hulík – Geometrica que tuvo lugar en el Museo Hranice, en 2019

 

Pero, si nos adentramos en los grandes números en matemáticas, el más famoso de todos es sin lugar a dudas, el googol. De hecho, en matemáticas es relativamente normal inventarnos nombres y notaciones para números grandes. Así lo hicieron los matemáticos estadounidenses Edward Kasner y James R. Newman en su libro Matemáticas e Imaginación (1940), que se inventaron el número “googol”, al que le dieron el valor de 10100 (un 1 seguido de 100 ceros), es decir, diez mil hexadecillones.

10.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000

Según se cuenta el nombre “googol” fue inventado por el sobrino de 9 años de Edward Kasner. En concreto, en el libro Matemáticas e Imaginación está escrito lo siguiente.

Palabras de sabiduría pronuncian los niños, por lo menos tan a menudo como los hombres de ciencia. El nombre “googol” fue inventado por un niño (sobrino del doctor Kasner, de nueve años de edad), a quien se le pidió que propusiera un nombre para un número muy grande, a saber: un 1 seguido de cien ceros. Estaba muy seguro de que este número no era infinito y, por lo tanto, igualmente en lo cierto de que debía tener un nombre. Al mismo tiempo que indicó la palabra “googol”, sugirió el nombre de otro número aún mayor: “googolplex”. El googolplex es mucho mayor que el googol, pero continúa siendo finito, como se apresuró a señalar el inventor de su nombre. Primero se sugirió que un googolplex sería un 1 seguido por tantos ceros que uno se cansase de escribirlos. Esto es una descripción de lo que sucedería si uno tratara realmente de escribir un googolplex, pero distintas personas se cansan en tiempos diferentes […].

A continuación, como la definición de googolplex como “un 1 seguido por tantos ceros que uno se cansase de escribirlos” no era muy rigurosa, ya que “pero distintas personas se cansan en tiempos diferentes”, entonces se definió el googolplex como 10 elevado a un googol:

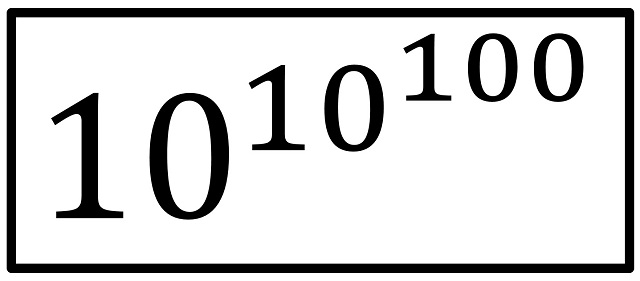
Es decir, un 1 seguido de un googol de ceros.

Pero, volviendo a la primera definición “un 1 seguido por tantos ceros que uno se cansase de escribirlos”, que ha sido sustituida por “un 1 seguido de un googol de ceros”, la verdad es que hemos pegado un salto cualitativo ya que no disponemos de tiempo para escribir un googol de ceros, ni siquiera aunque viviéramos tanto como la edad de nuestro universo. Supongamos que cada segundo escribimos tres ceros, que escribimos a ese ritmo de forma incansable, sin parar, toda la edad de nuestro universo, que son 13.787 millones de años, entonces escribiríamos tan solo

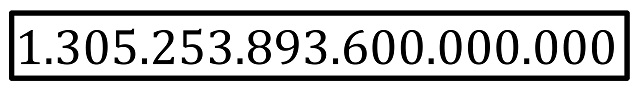
ceros. Y nos quedamos lejos del googol, ya que esa cantidad es del orden de 10 elevado a 18, es decir, un 1 seguido de 18 ceros, lejos de los 100 del googol.

Por otra parte, aunque parezca mentira estos números, el googol y el googolplex, han gozado de una cierta popularidad. Por ejemplo, el googol apareció en una de las tiras de humor de Snoopy, que vemos en la siguiente imagen. En ella puede verse a los personajes de Schroeder y Lucy juntos, entonces esta le pregunta a su amigo “Schroeder, ¿cuál crees que es la probabilidad de que me case algún día?” y su amigo le contesta “yo diría que una entre un googol”, y Lucy le pregunta qué es un googol y la respuesta de Schroeder en la viñeta es literalmente un uno seguido de 100 ceros, lo cual llena media viñeta, y Lucy se queda con cara de circunstancias).

Copyright Peanuts Worldwide LLC. Fair use

Mientras que el googolplex ha aparecido en series como Los Simpson, donde hay un cine que se llama Googolplex, o en la serie de dibujos Phineas y Ferb, donde hay un centro comercial con ese mismo nombre.

Centro comercial Googolplex en la serie Phineas y Ferb. Imagen tomada de Phineas and Ferb Wiki

 

Por otra parte, el nombre del buscador más famoso de internet Google, le debe su nombre a este número, al googol. La historia es la siguiente, según puede leerse en la página de David Koller, de la Universidad de Standford (California), donde se creó google.

En 1996, los estudiantes de doctorado de la Universidad de Stanford Larry Page and Sergey Brin inventaron un magnífico buscador que inicialmente bautizaron con el nombre de «BackRub», nombre que estaba relacionado con el proceso que realizaba el buscador, pero que no era muy atractivo, ni comercial. Y empezaron a buscar un nuevo nombre para el buscador, que fuera más apropiado. En una sesión de “lluvia de ideas” de Larry Page, junto con otros estudiantes de doctorado, entre ellos Sean Anderson, este propuso verbalmente el nombre de «googolplex» y Larry contestó que mejor «googol». Entonces, Sean se sentó en un ordenador a buscar si el dominio de internet de “googol” estaba libre, pero lo escribió mal, escribió “google.com”, en lugar de “googol.com” (en inglés ambas palabras se pronuncian de forma parecida, algo así como “gúgol”). Resultó que “google.com” estaba libre y a Larry Page le gustó el nombre y lo registró.

Logo de Google desde 2015

 

Pero eso de inventarnos números grandes no es algo moderno. Por ejemplo, en la Antigua India tenían diferentes palabras para números grandes. Por ejemplo, Asankhyeya, que significa literalmente «incontable» en sánscrito, es un número que equivale a 10140 (1 seguido de 140 ceros). Asankhyeya es una palabra que aparecía a menudo en los textos budistas y que venía a significar una cantidad infinita.

Aunque un número realmente gigante, volviendo a las matemáticas, es el número de Skewes, que es “diez elevado a diez elevado a diez elevado a 34”,

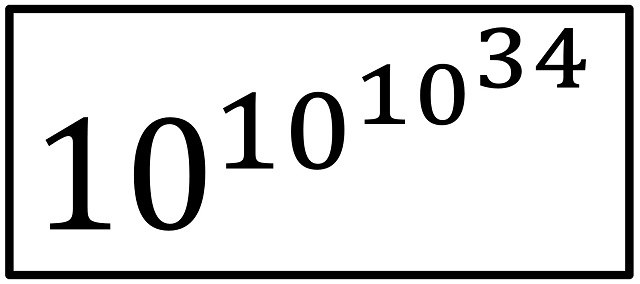
que durante un tiempo fue el número más grande que aparecía en una demostración matemática (en concreto, en un artículo del año 1933). Este número está relacionado con la distribución de los números primos, con la conocida Hipótesis de Riemann, pero ese es otro tema.

La verdad es que hemos pegado un salto muy grande. Volvamos un poco para atrás. Podríamos preguntarnos cuál es el número más grande que se puede formar con tres cifras, sin utilizar otros signos matemáticos. En un principio podríamos pensar que quizás fuese 999, pero resulta que no es así. El número más grande que se puede formar con tres cifras es

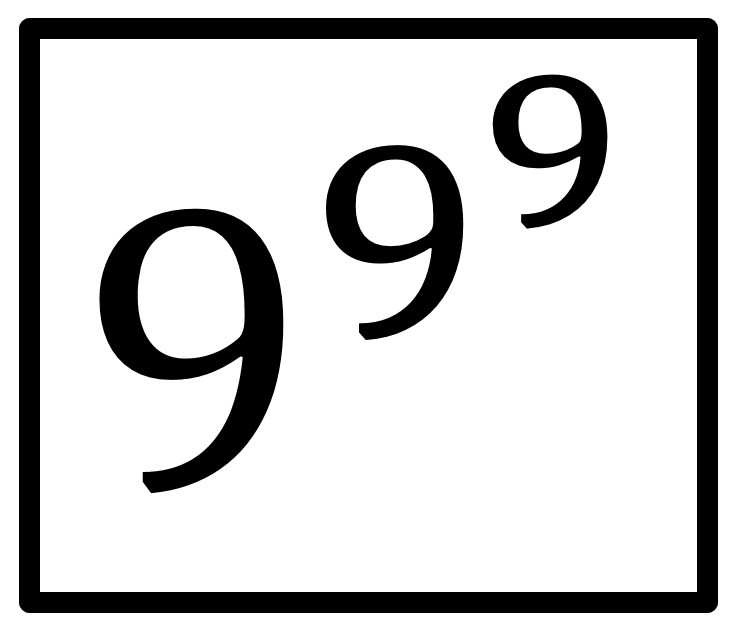
es decir, nueve elevado a nueve elevado a nueve. A este número le ocurre como a muchos otros grandes números, que a pesar de la sencillez con la que los expresamos, sin embargo, es difícil calcularlo y tener información sobre el mismo. Por ejemplo, ¿cómo de grande es este número (nueve elevado a nueve elevado a nueve)? Podríamos empezar por calcular 9 elevado a 9, que es 387.420.489, luego nuestro número es 9 elevado a este número, y esto no es sencillo de calcular. En 1906 se demostró que este, aparentemente sencillo número, tiene 369.693.100 dígitos (¡más de 369 millones de dígitos!).

Para hacernos una idea del orden de magnitud de este número (que es mayor que el googol, pero mucho más pequeño que el googolplex), imaginemos que lo queremos escribir, y lo vamos a hacer dedicando, de media, un segundo por cada cifra escrita y turnándonos varios amigos en la tarea para no parar de escribir en ningún momento. Tardaríamos entonces 11 años, 263 días, 20 horas, 31 minutos y 40 segundos en escribir el número “9 elevado a 9 elevado a 9”.

Pero, además, ¿cuánto espacio necesitaríamos para escribirlo? Si tomamos una hoja de papel, podemos escribir en una página 2.100 caracteres –30 líneas de 70 espacios cada línea-, entonces se precisarían 176.045 páginas de papel (la última solamente escrita hasta la tercera parte). Si, una vez escritas todas estas hojas de papel (que están escritas por una sola cara), queremos almacenarlas, ¿cuánto espacio nos ocuparán físicamente estos papeles sobre los que hemos escrito el número “9 elevado a 9 elevado a 9”? Cada hoja de papel tiene, más o menos, un grosor de 0,1 mm por hoja, luego 1000 hojas tienen un grosor de 100 mm, luego la cantidad de hojas escritas con el mencionado número ocuparán más de 18 metros de altura.

Las cuatro columnas de Montjuic (1919, reconstruidas en 2010), obra del arquitecto Puig i Cadafalch (1867-1956), tienen 20 metros de altura. Imagen de Canaan, en Wikimedia Commons

Volviendo a números grandes que aparecen en demostraciones matemáticas, como el número de Skewes (10 elevado a 10 elevado a 10 elevado a 34), en el libro Guinness de los Records de 1980 aparece el número de Graham como el “número más grande que aparece en una demostración matemática”, frase que escribió el divulgador Martin Gardner en su columna de Juegos Matemáticos de Scientific American en 1977. Pero su definición es lo suficientemente compleja para que lo dejemos para otra ocasión.

Bibliografía:

1.- K. C. Cole, El universo y la taza de té. Las matemáticas de la verdad y la belleza, Ediciones B, 1999.

2.- André Jouette, El secreto de los libros, Ma non tropo, 2000.

3.- Edward Kasner, James R. Newman, Matemáticas e imaginación, Salvat, 1986.

4.- Clifford A. Pickover, El prodigio de los números, Ma non troppo, 2002.

5.- Raúl Ibáñez, Las matemáticas como herramienta de creación artística, Catarata, 2023 (pendiente de publicación).

Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica

(*) Nota del editor:

En puridad el valor otorgado a los términos billón, trillón u otros depende de que en una comunidad de hablantes se empleen las escalas numéricas corta o larga. Esta asignación ha variado a lo largo de la historia y no es homogénea en el mundo. En general, en los países colonizados por Inglaterra se emplea la escala corta pero no es algo exacto. Así, es probable que un canadiense francófono use la escala larga, mientras que uno anglófono use la corta. Una persona británica, una ucraina o una brasileña usarán la corta, pero una portuguesa, una española o una argentina usarán la larga. Sobre todo esto véase: Long and short scales. Por simplificar, y por ser cierto en sentido estricto, matenemos el texto original de Raúl.

El artículo Un pequeño paseo por los grandes números se ha escrito en Cuaderno de Cultura Científica.

Marie Skłodowska Curie, una diminuta física polaca que vivió la mayor parte de su vida en París, es una de las científicas más famosas a nivel mundial; no solo fue una mujer pionera en un mundo dominado por los varones, también fue la primera persona en recibir dos premios Nobel. Einstein y Curie no tuvieron una relación especialmente estrecha, pero su fama simultánea aseguró que se encontrasen a menudo y mantuviesen una sólida amistad.

Einstein y curie en la época en la que se conocieron

Marie Curie ganó su primer premio Nobel, en física, en 1903, y el segundo, en química, en 1911. Trabajó teniendo a su marido, Pierre Curie (1859-1906), como colaborador en la analítica física, y a los químicos Gustave Bémont y André Devierne como colaboradores en la analítica química [1]. Curie ganó los premios Nobel por el descubrimiento de los elementos radioactivos polonio y radio, fundando a efectos prácticos la ciencia de la radioactividad. La pareja recibió su primer premio juntos, pero Pierre murió atropellado por un coche de caballos antes de que Curie ganase el segundo.

Einstein conoció a Curie no mucho después de que ella ganase su segundo premio Nobel. Ambos fueron invitados a la Primera Conferencia Solvay en Bruselas. Poco después de la conferencia, Curie escribió una recomendación profesional para el desenvuelto físico de 31 años. Dijo, “He admirado mucho los trabajos publicados por Monsieur Einstein en cuestiones concernientes a la física teórica moderna. […] en Bruselas, donde asistí a una conferencia en la que Monsieur Einstein participó, pude apreciar la claridad de su mente, la amplitud de su documentación y la profundidad de su conocimiento. Si se considera que Monsieur Einstein es aún muy joven, se tiene todo el derecho para depositar las mayores esperanzas en él y verle como uno de los teóricos importantes del futuro”. Einstein y Curie se hicieron amigos en la conferencia, llevando incluso a sus hijos de excursión juntos a un paso en los Alpes cerca de Engadine en 1913.

Imagen de la primera conferencia Solvay de 1911. Paul Langevin aparece de pie, primero por la derecha, al lado de Einstein. La foto corresponde a la época en la que se descubrió el affaire

Einstein fue una de las muchas figuras prominentes que acudieron en ayuda de Curie cuando fue atacada en la prensa por una aventura que tuvo con Paul Langevin, alumno de Pierre Curie, más joven que ella y casado. Aunque la historia ha demostrado que sí ocurrió, Curie siempre lo negó. Einstein creyó a Curie y afirmó que los rumores eran estupideces. “Ella no es lo suficientemente atractiva como para llegar a ser peligrosa para nadie”, declaró. Una afirmación muy interesante viniendo de un hombre que tendía a tener problemas con las mujeres (y que más de una vez sucumbió a esos asuntos “peligrosos”). Esta frase de Einstein nos habla también del germen y la calidad de la larga amistad intelectual entre Einstein y Curie. Curie era su igual, el que fuese una mujer era una anécdota irrelevante. [2]

Los dos físicos también coincidieron brevemente en política mundial. En 1922, Curie fue clave a la hora de convencer a Einstein para que se uniera a la recientemente constituida Comisión Internacional de Cooperación Intelectual, dependientemente de la Sociedad de Naciones. En esta comisión, aparte de Einstein y Curie, estaban, entre otros, Henri Bergson, Bela Bartók, Thomas Mann, Salvador de Madariaga y Paul Valéry. Curie escribió “Mi sensación es simplemente que la Sociedad de Naciones, aunque aún imperfecta, es una esperanza para el futuro”. Durante un tiempo Einstein estuvo de acuerdo, pero menos de un mes después de su incorporación, las posiciones políticas de Einstein se vieron alteradas por el asesinato del ministro alemán de exteriores, el judío Walther Rathenau. Consternado por estar representando a Alemania en la Comisión, Einstein escribió a Curie, “Me he dado cuenta de que un antisemitismo muy fuerte reina en el entorno que se supone represento en la Sociedad de Naciones y […] no puedo estar de acuerdo con este papel de representante o mediador. Pienso que lo comprenderás perfectamente”. Curie no lo comprendió. Intentó que cambiase de opinión, y finalmente Einstein volvió para otro período con la sociedad.

Tras años de exposición a la radiación debido a su trabajo, Marie Curie murió el 4 de julio de 1934. Un año después, Einstein escribió un elogioso homenaje para un acto en recuerdo a Curie el 23 de noviembre de 1935, en el Museo Roerich de Nueva York:

“Fue para mí una fortuna estar unido a Madame Curie durante veinte años de sublime y perfecta amistad. Llegué a admirar su grandeza humana sin límite. Su fuerza, su pureza de voluntad, su austeridad consigo misma, su objetividad, su juicio incorruptible, todas estas son virtudes que raramente se encuentran en un solo individuo.”

Notas:

[1] Ni Marie ni Pierre tenían formación suficiente en química como para realizar el procesado de los minerales originales. Dependieron para ello de químicos experimentados. Véase sobre esto: Gustave Bémont, el fantasma de la rue Vauquelin

[2] Poco después de la conferencia Solvay y con todo el revuelo mediático Einstein escribió a Curie:

«Muy estimada señora Curie:

No se ría de mí por escribirle sin tener nada sensato que decir. Pero estoy tan enfurecido por la manera tan vil en que el público se atreve actualmente a ocuparse de usted, que es absolutamente necesario que dé rienda suelta a este sentimiento. Sin embargo, estoy convencido de que usted desprecia sistemáticamente a esta chusma, tanto si le prodiga servilmente respeto como si intenta saciar su ansia de sensacionalismo.

Me veo obligado a decirle lo mucho que he llegado a admirar su intelecto, su empuje y su honestidad, y que me considero afortunado de haberla conocido personalmente en Bruselas. Cualquiera que no se encuentre entre estos reptiles se alegra, ahora como antes, de que tengamos entre nosotros a personajes como usted, y también a Langevin, personas reales con las que uno se siente privilegiado de estar en contacto. Si la chusma sigue ocupándose de usted, simplemente no lea esa bazofia, sino déjela para el reptil para el que ha sido fabricada.

Con los más cordiales saludos para usted, Langevin y Perrin, muy atentamente,

A. Einstein

P.D. He determinado la ley estadística del movimiento de la molécula diatómica en el campo de radiación de Planck mediante una ocurrencia cómica, naturalmente bajo la restricción de que el movimiento de la estructura sigue las leyes de la mecánica estándar. Sin embargo, mi esperanza de que esta ley sea válida en la realidad es muy pequeña».

– Albert Einstein, 23 de noviembre de 1911.

Fuente

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

Una versión anterior de este artículo se publicó en Experientia Docet el 19 de julio de 2009

El artículo Einstein y Marie Skłodowska Curie se ha escrito en Cuaderno de Cultura Científica.

A lo largo de todas estas entradas de Planeta B hemos remarcado la importancia de los meteoritos en el conocimiento de la geología de nuestro Sistema Solar, ya que nos abren la puerta a estudiar no solo la composición, sino también algunos procesos ocurridos a lo largo de la historia en aquellos cuerpos de los que proceden, y de los que en la mayoría de las ocasiones carecemos de muestras traídas directamente.

Pero no solo eso, los meteoritos nos pueden aportar una visión histórica sobre nuestro planeta -y el Sistema Solar en general- más prolongada que las rocas que hoy día podemos encontrar en la Tierra, ya que esas primeras rocas desaparecieron fruto de los impactos de los asteroides, la erosión y la tectónica de placas.

Una condrita carbonácea, un tipo de meteorito que en algunos casos puede contener un gran porcentaje de agua. Imagen cortesía de NASA / Eric James.

Dicho esto, si queremos conocer mejor como fueron esos ladrillos fundamentales que dieron lugar a nuestro planeta para intentar reconstruir con mayor detalle cómo pudo ser esa infancia de la Tierra, tenemos que recurrir, sin duda, al estudio de los asteroides y los meteoritos.

Y es que, aunque las últimas décadas nos han sido muy gratas en cuanto a descubrimientos, nos quedan todavía muchos interrogantes. Uno de estos, y que de algún modo sigue sujeto a gran debate científico, es ¿de dónde proviene el agua de nuestro planeta? ¿Formaba parte de la Tierra durante su formación o llegó después a partir de los impactos de cometas y asteroides?

Estudios recientes sugieren que alrededor del cinco por ciento de la masa de nuestro planeta podría provenir de las zonas más externas de nuestro Sistema Solar, un lugar dominado por gases y elementos volátiles -como el agua-, pero cuya proporción puede haber ido variando a lo largo del tiempo, especialmente tras el impacto que dio lugar a la formación la Luna.

Pero con estos estudios surgen nuevas dudas… ¿incorporó la Tierra estos elementos volátiles antes o después de su formación? Quizás está aquí el quid de la cuestión.

¿Proviene el agua del impacto de cuerpos ricos en hielo como los cometas, y que impactaron sobre nuestro planeta en etapas tardías? Imagen cortesía de ESA/Rosetta/NAVCAM

Para poder responder a estas preguntas, los científicos están intentando conocer con precisión las ratios isotópicas de los distintos elementos, ya que pequeñas variaciones en estas proporciones podrían significar que provienen de lugares diferentes o incluso que fueron incorporados a nuestro planeta en momentos diferentes, entre otros procesos.

Al intentar resolver el origen del agua en la Tierra tenemos que contar con el estudio de meteoritos que contengan agua, porque los isótopos del hidrógeno del agua podrían tener una de las claves, pero el agua no se encuentra distribuida de una manera homogénea dentro del meteorito.

¿Y qué tienen que ver los rayos X y los neutrones con el origen del agua? Un nuevo estudio publicado esta pasada semana nos abre una puerta a estudiar los meteoritos de una manera no invasiva antes de que sean usados para tomar muestras, ayudándonos a seleccionar los lugares más interesantes del meteorito combinando ambas técnicas.

Vídeo del interior del meteorito GRA 06100, recogido en la Antártida. Los colores azules muestran los compuestos con hidrógeno, como el agua. Los rojos muestran compuestos ricos en hierro. Vídeo cortesía de NIST.

El estudio con neutrones nos permite, dentro del meteorito, buscar las zonas con mayor contenido en agua y compuestos del hidrógeno, mientras que los rayos X nos permiten ver mejor compuestos con elementos de mayor peso atómico, como los metálicos. Estas dos técnicas combinadas permiten realizar un modelo tridimensional del interior del meteorito con las que los científicos podrían decidir que zonas son más adecuadas para el análisis para medir las ratios isotópicas del hidrógeno y así, quizás, conseguir mejores respuestas de cara al origen del agua.

Esta técnica, además, permitirá elaborar mapas composicionales que nos permitirán conocer, sin tener que cortar, la relación entre los distintos elementos que hay en el interior de los meteoritos, estudiar el alcance de la alteración física y química que estos han sufrido y su estructura sin necesidad de destruir la muestra para su estudio, preservándolas para estudios futuros.

Sin lugar a dudas, esta técnica no solo será útil para el estudio de los meteoritos, sino que podrá abrirse a otros campos de la geología e incluso, quien sabe, si a las muestras que seamos capaces de traer de Marte en la década de 2030.

Para saber más:

Métodos no destructivos para analizar muestras marcianas
Las últimas gotas de agua en el meteorito

Bibliografía:

Borg, L.E., Brennecka, G.A. and Kruijer, T.S. (2022) “The origin of volatile elements in the earth–moon system,” Proceedings of the National Academy of Sciences, 119(8). doi:: 10.1073/pnas.2115726119.

Treiman, A.H. et al. (2022) “Coordinated Neutron and x‐ray computed tomography of meteorites: Detection and distribution of hydrogen‐bearing materials,” Meteoritics & Planetary Science, 57(10), pp. 1820–1835. doi: 10.1111/maps.13904.

Sobre el autor: Nahúm Méndez Chazarra es geólogo planetario y divulgador científico.

El artículo Rayos X y neutrones para descubrir el origen del agua en la Tierra se ha escrito en Cuaderno de Cultura Científica.

Foto: Alex Bodini / Unsplash

Si le digo que la prolactina es la hormona de la que depende la producción de leche en los mamíferos, pensará, inmediatamente, que es una hormona femenina. Pero en biología, máxime en materia de sexo, a menudo las cosas no son lo que parecen. Sus funciones más importantes tienen que ver con la reproducción, pero cumple, además, papeles esenciales en otros procesos.

La pituitaria, o hipófisis, es el principal órgano endocrino que produce prolactina. Ese órgano, de muy pequeño tamaño, se encuentra en la base del encéfalo. La zona concreta que produce prolactina recibe señales del hipotálamo, una región encefálica que constituye, por así decir, la interfase entre el sistema nervioso y el sistema hormonal. Las señales procedentes del hipotálamo llegan a la hipófisis, mediante un servicio de mensajería química a través de su propio sistema de vasos y capilares sanguíneos. De esa forma, el control último de la liberación de la hormona corresponde al sistema nervioso. La arquitectura y organización de todo este dispositivo de control es, a la vez, compleja y elegante.

Un grupo importante de funciones en las que interviene la prolactina tiene que ver con el cuidado parental, esto es, con la atención y, sobre todo, la alimentación de las crías. En el caso de la producción de leche, esa función es clara. Durante el embarazo aumenta la concentración sanguínea de prolactina, las células de las glándulas mamarias empiezan a acumular reservas y, como consecuencia, las mamas se agrandan. Al final del embarazo, con el parto, desciende la concentración sanguínea de progesterona y estrógenos. Ese descenso, junto con las señales de succión en los pezones, hacen que las glándulas mamarias empiezan a producir leche. La oxitocina, otra hormona, provoca su eyección en respuesta a la succión por el bebé.

Pero no solo las hembras de mamífero se ven influidas por la prolactina. A los machos también nos afecta, y lo hace de manera que favorece las tendencias a cuidar de la prole. Los hombres, con la paternidad, experimentamos un descenso en la concentración sanguínea de testosterona y un aumento de la de prolactina. No producimos leche, claro está, pero nuestro comportamiento se modifica, reduciéndose la agresividad y adquiriendo una actitud “paternal” para con nuestras criaturas. No somos los únicos mamíferos en los que ocurren estas cosas. En general y hasta donde se ha investigado, se trata de respuestas fisiológicas propias de los machos que intervienen en el cuidado y atención de su prole.

Hay comportamientos aún más extremos que el masculino humano. El tití Callithrix jacchus y el tamarino Saguinus oedipus son primates, monos del Nuevo Mundo, y monógamos. No es muy habitual que los primates sean monógamos, pero estos lo son. Los machos de estas especies se ocupan de su progenie a fondo, hasta el punto de que, tras el parto, le dedican más tiempo de atención y cuidados que las madres. No hay ningún comportamiento semejante en el mundo mamífero. El fenómeno es tan relevante, que el cuidado de la cría hace que el padre pierda peso. Hasta tal punto es importante que, para poder estar preparados para la paternidad, estos monos ganan peso durante el embarazo de sus parejas. Desde que la mona se queda embarazada hasta que da a luz, el padre gana un 15% de peso, ganancia que más adelante se esfumará. Pues bien, la hormona que participa en este fenómeno es –ya lo habrá adivinado– la prolactina, la hormona que, entre otras funciones menos llamativas, interviene en el cuidado maternal de las crías y, dependiendo de las circunstancias, también del paternal.

Para saber más:

El enamoramiento como droga de abuso

Fuente: Ziegler, T. E., Prudom, S. L., Schultz-Darken, N. J., Kurian, A. V., Snowdon, Ch. T. (2006): Pregnancy weight gain: marmoset and tamarin dads show it too. Biol. Lett. 2: 181–183. doi: 10.1098/rsbl.2005.0426

 

Sobre el autor: Juan Ignacio Pérez (@Uhandrea) es catedrático de Fisiología y coordinador de la Cátedra de Cultura Científica de la UPV/EHU

El artículo La hormona de la maternidad y de la paternidad se ha escrito en Cuaderno de Cultura Científica.

Bilbao volvió a acoger el pasado 20 de mayo de 2022 “Las pruebas de la educación”, una jornada que abordará diversas cuestiones educativas con la evidencia científica existente. Esta quinta edición está organizado por la Cátedra de Cultura Científica de la UPV/EHU y la Fundación Promaestro con la colaboración del Consejo Escolar de Euskadi, y se celebró en el Bizkaia Aretoa – UPV/EHU de la capital vizcaína.

La jornada consta de cinco ponencias de media hora de duración en la que se tratan temas como la problemática relacionada con los juegos de azar en el ámbito escolar, el impacto de la inmigración en el rendimiento del alumnado o el debate sobre la jornada escolar continua o partida, entre otras cuestiones. La dirección del seminario corrió de nuevo a cargo de Marta Ferrero profesora de la Facultad de Formación del Profesorado y Educación de la Universidad Autónoma de Madrid.

El hecho de que un gran porcentaje de docentes de Educación Primaria sufran un rechazo por las Matemáticas condicionan su manera de abordarla. En esta conferencia Rocío Garrido-Martos, profesora de Didáctica de las Matemáticas en la Universidad Autónoma de Madrid (UAM), analiza algunas de las posibles razones de este rechazo y como condiciona la dimensión afectiva en el aprendizaje y enseñanza de estas ciencias.

 



 

Edición realizada por César Tomé López a partir de materiales suministrados por eitb.eus

El artículo Las pruebas de la educación: Rocío Garrido Martos – La dimensión afectiva y la didáctica de las matemáticas se ha escrito en Cuaderno de Cultura Científica.

Una supernova es una explosión estelar que se produce al final de la vida de algunas estrellas muy masivas. En este violento epílogo, una onda de choque expulsa el material de las capas exteriores de la estrella, lo que permite observar los diferentes elementos de los que estaba compuesta.

Un equipo internacional, en el que ha participado Tom Broadhurst, Investigador Ikerbasque de la Universidad del País Vasco (UPV/EHU) y asociado del Donostia International Physics Center (DIPC), ha obtenido tres imágenes, cada una en una frecuencia diferente, de una misma supernova en el universo distante, gracias al poder magnificador de una galaxia ubicada en primer plano.

El equipo de investigación desarrolló un modelo del campo gravitacional de la galaxia que sirvió de lente y así se pudo determinar que la luz de estas tres imágenes recorrió tres caminos diferentes, que difieren en distancia por unos pocos días (la distancia se mide en tiempo porque la velocidad de la luz es constante). Esto explica las tres frecuencias obtenidas en las imágenes, ya que a medida que el gas de la supernova se expande y se enfría existe una variación en la frecuencia emitida. A mayor temperatura, la luz emitida es más violeta (incluso ultravioleta), y a medida que la temperatura va disminuyendo, la luz emitida va tendiendo al rojo. Así, la imagen azul corresponde a una fotografía de la supernova unas pocas horas después de la explosión estelar, mientras que las imágenes verde y roja corresponden a 2 y 8 días tras la explosión respectivamente.

Esta información permitió determinar el radio de la estrella original, una supergigante roja con un radio equiparable a 500 veces el del Sol, y que explotó hace 11.500 millones de años, mucho antes de que existiera la Tierra, en la época en la que se considera que se formó nuestra Galaxia. Las imágenes de esta supernova, captadas con el Telescopio Espacial Hubble, están muy magnificadas por el campo gravitacional de una galaxia más cercana que actúa como lente, lo que nos permite ver mucho más lejos en distancia, y en el tiempo, que todas las supernovas locales en galaxias cercanas.

El estudio de las explosiones de estas estrellas supergigantes rojas encaja con la idea actual de cómo los núcleos de los elementos más pesados se habrían creado dentro de las estrellas y liberados al espacio durante las explosiones de supernovas. De esta manera los elementos forjados en el interior de las estrellas tras estas explosiones de supernova se convierten en la siguiente generación de gas y polvo a partir de los cuales se crean los sistemas solares y la vida tal y como la conocemos. Sin las supernovas el gas en las galaxias actuales solo incluiría hidrógeno, helio y algo de litio que se formaron en el Big Bang y no soportaría la vida compleja que requiere de otros elementos químicos más pesados.

Es importante destacar que esta supernova observada a través de una lente gravitacional demuestra que un evento ocurrido en el universo lejano se puede presenciar varias veces, por lo que, en principio, cuando se detecte una nueva supernova podríamos enfocar nuestros instrumentos con anticipación para ver en detalle la aparición de esa misma supernova.

Para saber más:

Vida y muerte de una estrella

Referencia:

W. Chen, P. L. Kelly, M. Oguri, T. J. Broadhurst, J. M. Diego, N. Emami, A. V. Filippenko, T. L. Treu, A. Zitrin (2022) Shock cooling of a red super-giant supernova at redshift 3, in lensed images Nature doi: 10.1038/s41586-022-05252-5

Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa

El artículo Las lentes gravitacionales permiten observar la aparición de una supernova varias veces se ha escrito en Cuaderno de Cultura Científica.

Ahora que cierta serie inspirada en el universo creado por J. R. R. Tolkien se ha convertido en un fenómeno de masas me he acordado de una curiosa anécdota que tuve junto a varias amigas y amigos geólogos hace unos años, cuando fuimos al cine a ver el estreno de “El Hobbit: La Batalla de los Cinco Ejércitos”. En la parte de la película que ALERTA SPOILER sucede en Dol Guldur, cuando Lady Galadriel se enfrenta a Sauron, ocurre un curioso efecto visual con la imagen del nigromante, que parece repetirse al cambiar la escala y de manera cíclica hasta ser expulsado a Mordor. En ese instante dijimos en mitad del cine, reconozco que igual con voz demasiado elevada, “¡Anda mira, Sauron fractal!” FIN DEL SPOILER.

La verdad es que no se trataba de un fractal en sentido estricto, pero nos dio pie a una interesante discusión sobre la relación entre la geometría fractal y la geología.

No voy a explicar lo que es un fractal, ya que es un concepto matemático que, ni de lejos, es mi especialidad, pero, de manera muy resumida, se caracterizan por dos propiedades: 1- se trata de morfologías muy complejas que no pueden explicarse con la geometría euclídea tradicional; y 2- estas morfologías se repiten al modificar la escala, es decir, mantienen la misma forma independientemente de si las observamos al microscopio o a tamaño kilométrico. Y estas morfologías fractales son muy comunes en la naturaleza, pudiendo encontrar muchos ejemplos en el ámbito geológico.

Muestra del mineral pirita, cuya composición química es FeS2, cristalizado en el sistema cristalino cúbico. La longitud de la arista es de 7cm.

Uno de los más evidentes lo observamos en la estructura cristalina de los minerales. Un mineral no aparece de la nada, sino que tiene un nacimiento, por así decirlo, que se produce cuando se unen varios átomos o moléculas con una composición química concreta. Si este embrión mineral tiene suficiente tiempo y espacio, va a ir agregando más elementos o moléculas químicas, lo que le permite crecer en tamaño. Pero este crecimiento lo hace siempre manteniendo la misma estructura cristalina, es decir, la misma morfología, por ejemplo, un cubo. De esta manera, nos podemos topar con cristales de un mismo mineral que sean cubitos de apenas unos milímetros de longitud de arista, o con cristales que puedan llegar a medir varios centímetros o metros de longitud, teniendo unos cubos de categoría. Vamos, que conservan la misma forma independientemente del tamaño final que alcance el cristal.

Río braided o trenzado de Islandia a vista de dron. Fotografía de Iurie Belegurschi / Iceland Photo Tours

Voy a pasarme ahora al mundo de la geomorfología. Seguro que os habéis dado cuenta de que no todos los ríos del mundo tienen la misma forma. Esta morfología depende del clima, el caudal de agua que transportan y las características geológicas del terreno que atraviesan. Pues hay un tipo de ríos donde la geometría fractal es más que evidente. Se trata de los ríos braided, que podríamos traducir como de tipo trenzado. Son unos ríos de grandes dimensiones cuya forma recuerda mucho a las ramas de los árboles o al sistema circulatorio, ya que tienen un canal principal y muchos canales secundarios que se van ramificando en canales cada vez más pequeños. Pues este patrón de distribución sigue una geometría fractal, ya que se repite a cualquier escala de observación que utilicemos. De tal manera que, si hacemos un zoom sobre uno de los canales secundarios, veremos cómo parten de él canales menores formados por otros canales cada vez más pequeños.

Fósil de la concha de un ammonites con sutura ammonítica.

Y no podía dejar pasar la oportunidad de hablar de fósiles, así que voy a terminar con un tercer ejemplo también bastante curioso. Los ammonites son un grupo de cefalópodos marinos ya extintos que formaban una concha carbonatada que iba creciendo con forma de espiral. Este crecimiento, debido a su vez al crecimiento del propio organismo, se producía por la adicción de una nueva cámara más grande que albergaba las partes blandas. La unión entre las cámaras se denomina sutura que, a modo de símil, representaría las costuras entre las cámaras. Pues hay un tipo de sutura conocida como ammonítica que tenía una morfología sinuosa formada por curvas superpuestas una sobre la otra, que recuerda mucho a las suturas craneales. De nuevo, resulta que este patrón de curvas superpuestas se repite a diferentes escalas, manteniendo una morfología fractal.

Aquí solo he usado tres ejemplos muy evidentes, pero existen decenas de procesos, estructuras y eventos geológicos que pueden cuantificarse y explicarse empleando la geometría fractal. Os invito a que los busquéis, porque son realmente curiosos. Y, por supuesto, esto no es más que una simple muestra de la estrecha relación que existe entre la Geología y las Matemáticas y de cómo se mantiene la armonía en la naturaleza.

Sobre la autora: Blanca María Martínez es doctora en geología, investigadora de la Sociedad de Ciencias Aranzadi y colaboradora externa del departamento de Geología de la Facultad de Ciencia y Tecnología de la UPV/EHU

El artículo Geometría fractal y geología, morfologías que se repiten al modificar la escala se ha escrito en Cuaderno de Cultura Científica.

Will Rogers (1879-1935) fue un actor cómico estadounidense a quien se atribuye la mordaz frase: «When the Okies left Oklahoma and moved to California, they raised the average intelligence level in both states» («Cuando los habitantes de Oklahoma se mudaron a California, aumentaron el nivel de inteligencia medio en ambos estados»).

Will Rogers. Fuente: Wikimedia Commons.

 

Por este motivo se conoce como “efecto Will Rogers” (o paradoja de los Okies) a una familia de situaciones contraintuitivas que vamos a explicar en esta anotación.

Una paradoja con medias aritméticas

Consideremos dos conjuntos de números enteros positivos A = {5, 6, 7, 8, 9} y B = {1, 2, 3, 4}. La media aritmética de A es (5 + 6 + 7 + 8 + 9) / 5 = 7 y la de B es (1 + 2 + 3 + 4) / 4 = 2,5. Si trasladamos el número 5 de A hacia B, obtenemos los conjuntos A’ = {6, 7, 8, 9} y B’ = {1, 2, 3, 4, 5}. La media de A’ es (6 + 7 + 8 + 9) / 4 = 7,5 y la de B’ es (1 + 2 + 3 + 4 + 5) / 5 = 3. ¡Ambas medias aritméticas han aumentado! ¿No es esto paradójico?

Aparentemente lo es. Pero fijaos que en el conjunto A se ha eliminado en número menor, que es mayor que todos los enteros positivos del conjunto B…

El efecto Will Rogers y la salud pública

El efecto Will Rogers salva vidas… Y lo hace sin necesidad de tratar a ningún paciente. En efecto, supongamos que, gracias a la investigación científica y técnica, se amplían los criterios o la capacidad para identificar una enfermedad. Por este motivo, un grupo de personas pasa de la lista de “individuos sanos” al registro de “individuos enfermos”. Como esas personas padecían ciertamente esa enfermedad, estaban más enfermas que una persona sana promedio. Al retirarlas de la lista de “individuos sanos” aumenta la esperanza de vida (o la salud general) de la lista de personas sanas.

Por otro lado, estas personas diagnosticadas gracias a esos avances en investigación están menos enfermas que los pacientes más graves de la lista de “individuos enfermos”. Y es así, porque están en una etapa temprana o su afección es leve. Hasta que los criterios de evaluación de esa enfermedad no cambiaron, no se consideraban como personas enfermas, y ahora lo son. Pero como están en mejores condiciones de salud que los “individuos enfermos” según el método anterior, la esperanza de vida de este último registro sube.

Lo sorprendente de este fenómeno es que nadie ha recibido ningún tratamiento, por lo tanto, ninguna persona ha mejorado su salud por haberle diagnosticado esta enfermedad. Sin embargo, esta reclasificación implica que las personas de ambas listas han aumentado su esperanza de vida.

En el artículo de Feinstein et al. explican precisamente el caso de un grupo de pacientes con cáncer de pulmón tratados por primera vez en 1977. En ese momento tenían unas tasas de supervivencia (a los seis meses) más altas para el grupo total y para los subgrupos en cada uno de los tres estadios principales (tumor, ganglios y metástasis) que un grupo tratado entre 1953 y 1964 en las mismas instituciones. ¿Qué había sucedido? Que el grupo más reciente se había sometido a nuevos procedimientos de diagnóstico por imágenes, con lo que el pronóstico mejoró. Además, se observaron metástasis que antes no se podían identificar, con lo que los nuevos datos procedentes de la mejora de la tecnología médica llevaron a estos pacientes a un cambio de etapa. Muchos de esos individuos que previamente habrían sido diagnosticados en una fase “buena” fueron entonces asignados a una fase “mala”. En el nuevo grupo al que habían sido asignados, su estado de salud era mejor que el de la mayoría de las personas. Así, la tasa de supervivencia aumentó en cada grupo sin cambios en cada paciente individual. Además, antes de utilizar esos nuevos métodos diagnósticos, los dos grupos tenían tasas de supervivencia similares.

En una situación como la descrita arriba, el mero hecho de reordenar no cambia nada ni para el conjunto de la población, ni para cada individuo. Sin una acción adicional, no hay ningún beneficio real para ningún paciente.

En el ámbito de la medicina, muchas personas son conscientes de posibles sesgos en la interpretación estadística de los datos y en la posibilidad de estar a merced del efecto Will Rogers. Existen numerosos artículos que tratan de este tema; algunos de ellos están relacionados con el cáncer de próstata, el cáncer de mama, el cáncer de estómago, la esclerosis múltiple y muchas otras dolencias.

Volviendo a la frase de Will Rogers

Parece que con esta frase Will Rogers se refería a la época de la Gran Depresión de 1929. Cuando algunos trabajadores Okies se fueron a California a buscar empleo, en Oklahoma aumentó el coeficiente intelectual debido a la emigración (aludiendo a la falta de oportunidades de estas personas para estudiar y formarse). Rogers era originario de Oklahoma y, orgulloso de sus orígenes, insinuaba de manera jocosa que cualquier habitante de Oklahoma era más inteligente que el californiano medio… ¡Probablemente este comentario no hizo demasiado gracia en el estado de California!

Referencias

• Alvan R. Feinstein, M.D., Daniel M. Sosin, M.D., and Carolyn K. Wells, M.P.H., The Will Rogers Phenomenon — Stage Migration and New Diagnostic Techniques as a Source of Misleading Statistics for Survival in Cancer, N Engl J Med 312 (1985) 1604-1608

• Will Rogers phenomenon, Wikipedia

Sobre la autora: Marta Macho Stadler es profesora de Topología en el Departamento de Matemáticas de la UPV/EHU, y colaboradora asidua en ZTFNews, el blog de la Facultad de Ciencia y Tecnología de esta universidad

El artículo El efecto Will Rogers se ha escrito en Cuaderno de Cultura Científica.

Arthur Eddington creyó en las teorías de Einstein desde el principio, y fueron sus datos tomados durante el eclipse solar de 1919 los que dieron el primer indicio experimental de que la teoría general de la relatividad podría ser correcta. La amplia cobertura informativa de los resultados de Eddington llevó a la teoría de la relatividad, y al propio Einstein, a unos niveles de fama sin precedentes.

En la imagen, tomada en Leiden en 1923, podemos ver de arriba abajo y de izquierda a derecha a Albert Einstein, Paul Ehrenfest, Willem de Sitter, Arthur Eddington y Hendrik Lorentz. Fuente: Wikimedia Commons

Arthur Eddington está considerado uno de los más importantes astrónomos ingleses del siglo XX. Se especializó en la interpretación de las observaciones de los movimientos de las estrellas en el Observatorio de Greenwich. En 1913, fue uno de los primeros científicos no alemanes en entrar en contacto con las primeras versiones de la teoría general de la relatividad, e inmediatamente se convirtió en un declarado partidario.

Cuando Einstein empezó a publicar sobre la teoría general de la relatividad, Eddington, como otros muchos científicos, estaba convencido de que era correcta; simplemente tenía tanto sentido que sentían que tenía que ser correcta. Pero eso no significaba que no quisiesen ver una prueba concreta, experimental. Dado que la teoría de la relatividad general se centra en la idea de que las masas gigantescas (estrellas, planetas, etc.) deforman el mismísimo espacio (estrictamente, el espaciotiempo), la única forma de comprobar la teoría era la observación astronómica. Los científicos querían medir si la luz de una estrella se desviaba al pasar cerca de una masa como la del Sol. El problema era que esa observación de la débil luz de una estrella no se podía hacer con el Sol brillando con toda su intensidad. Era necesario un eclipse.

Y así en 1912, 1914 y 1916, se enviaron expediciones a varias localizaciones alrededor del mundo para estudiar eclipses solares. Pero cada una de ellas no pudo aportar datos: en la primera llovió y las segundas fueron detenidas por motivos geopolíticos (la Primera Guerra Mundial había comenzado en 1914). Sin embargo, esto terminó siendo una suerte ya que, si bien hoy sabemos la teoría de Einstein era correcta, en esas fechas un cálculo clave era erróneo. En la primera publicación de la teoría en 1911, Einstein había calculado mal el valor de la curvatura de la luz debida a la gravedad; se había descuidado a la hora de incluir todos los efectos del espacio curvado. Si los datos de los eclipses hubiesen estado en desacuerdo con las predicciones de Einstein, como probablemente habría ocurrido, la teoría podría haber sido desechada por incorrecta.

En 1915 Einstein corrigió el modelo matemático de la teoría, proporcionando un valor revisado para el arco de la luz. Hubo un intento de medición en 1918 en los Estados Unidos pero los resultados no fueron concluyentes.

Durante todos estos intentos, Eddington simplemente aceptó la teoría general de la relatividad, sin necesitar más pruebas que su razón, pero el director del Observatorio de Greenwich y Astrónomo Real, Frank Watson Dyson, quería ver los datos de una prueba “concluyente”[1]. Así, Dyson ordenó dos expediciones para 1919. Eligió a Andrew Crommelin del Observatorio Real para liderar una a la ciudad de Sobral (Brasil) y a Eddington para la otra. La elección de Eddington tuvo toda una historia detrás.

En 1917, el gobierno británico comenzó una nueva tanda de reclutamiento y, aunque la Universidad de Cambridge había movido los hilos para que no tocasen a su profesor, la crianza cuáquera de Eddington le llevó a denunciar formalmente la guerra. Dyson intervino y, usando toda su influencia, convenció al Ejército Británico de que se olvidase del científico bocazas. A cambio de no ir a un campo de prisioneros, el compromiso que adquirieron Eddington y Dyson fue que Eddington “encabezaría una expedición que aseguraría la tradición británica de estar a la vanguardia de la física de manera que el brillo de Newton no se viese empañado”. De esta forma Eddington fue el encargado de dirigir la expedición a la isla portuguesa de Príncipe (actualmente parte de Santo Tomé y Príncipe) en el Golfo de Guinea en África.

La expedición de Eddington fue todo un éxito mediático

Tan pronto como supo del éxito de los científicos británicos, Einstein mandó una postal a su madre. Decía: “Querida madre, felices noticias hoy. H.A. Lorentz me ha telegrafiado diciendo que las expediciones británicas han demostrado de hecho la deflexión de la luz por el Sol”. Los científicos también saludaron con entusiasmo los resultados, y posiblemente gracias a un profundo deseo de superar las divisiones de la Gran Guerra, el resto del mundo se alegró de que unos británicos hubiesen confirmado las teorías de un alemán. Eddington fue el encargado de presentar los resultados ante una reunión conjunta de la Royal Society y la Royal Astronomical Society. Los periódicos estaban encantados con la noticia. [2]

El Times de Londres afirmaba en sus titulares del 17 de noviembre de 1919. “Revolución en la ciencia – Nueva teoría del universo – Las ideas de Newton derrocadas”. Y antes incluso de que las noticias se difundiesen por Europa, el New York Times en los Estados Unidos escribía una serie de seis artículos con titulares como: “Luces torcidas en los cielos”; “Los hombres de ciencia más o menos convulsionados: la teoría de Einstein triunfa”. Eddington también pasó al primer plano. Era requerido para que diese conferencias continuamente y, en ellas, hablaba a menudo de la relatividad.

En 1920, Eddington publicaría una obra de divulgación “Espacio, tiempo y gravitación”. En 1923, la magistral “Teoría matemática de la relatividad”. Hasta su muerte ya no publicaría ningún trabajo relevante más, dedicando sus últimos 20 años de vida, al igual que Einstein, a la búsqueda infructuosa de una teoría unificada. En 1946 aparecería póstumamente su “Teoría fundamental”. La diferencia principal entre Einstein y Eddington estuvo en que Einstein era consciente de que ninguno estaba teniendo éxito en su búsqueda de la teoría del campo unificado.

 

Notas:

[1] Todo este relato tiene unas profundas implicaciones filosóficas. Sobre la necesidad de una prueba concluyente véase: El experimento crucial que nunca existió

[2] ¿Una sola medición echa por tierra todo el marco físico newtoniano? ¿O son los medios de comunicación los que elevan a absoluto un hallazgo preliminar en su búsqueda del titular impactante? Véase Desviación de la luz y falsabilidad y, para más detalle técnico, Comprobaciones experimentales de la relatividad general (y 2)

Sobre el autor: César Tomé López es divulgador científico y editor de Mapping Ignorance

Una versión anterior de este artículo se publicó en Experientia Docet el 15 de noviembre de 2009.

El artículo Einstein y Arthur Eddington se ha escrito en Cuaderno de Cultura Científica.

Sossusvlei, Namibia. Foto: Parsing Eye / Unsplash

La crisis climática, por el progresivo aumento de las temperaturas del planeta Tierra, es un fenómeno global del que nadie está a salvo. Sin embargo, su impacto no es ni será igual para todos. Determinados países son especialmente vulnerables a las consecuencias del calentamiento global porque apenas tienen recursos para hacerles frente. Además, sus poblaciones cuentan con condiciones de vida ya de por sí muy precarias y sus economías dependen en gran medida del clima. Se calcula que la crisis climática ha destruido un 20 % del producto interior bruto de los países más vulnerables. Precisamente por ello, de entre todas las regiones, el África es la más vulnerable frente a los diferentes escenarios que se plantean ante un calentamiento por encima de los 1,5 ºC desde la época preindustrial.

A pesar de que África apenas ha contribuido con un 3 % en las emisiones globales de dióxido de carbono, en comparación con el 62 % de Europa y América del Norte desde la Revolución Industrial, es la zona del planeta que más está sufriendo las consecuencias del calentamiento global. Unos daños que irán a más con el progresivo aumento de las temperaturas a lo largo de los años.

Se estima que torno al 95 % de los cultivos del África subsahariana dependen del agua de lluvia y que el 41 % de la población vive en tierras secas, proclives a las sequías. Desde 1970-79 hasta 2010-2019 las sequías en esta región se han triplicado. Esto ha acentuado la pobreza (por las pérdidas de las cosechas y del ganado) y provocado inseguridad alimentaria, enfermedades y muertes por desnutrición entre las personas más vulnerables de múltiples países africanos.

En torno a 1,7 millones de personas mueren cada año en África por las razones anteriores y los casos de desnutrición han aumentado un 50 % desde 2012 según la Organización de Naciones Unidas (ONU). Además, los ciclones, las inundaciones y la aparición de vectores han provocado migraciones masivas, millones de muertos y potenciado la aparición de diversas enfermedades infecciosas: malaria, ébola, fiebre de Lassa, dengue, enfermedad de Lyme, virus del Nilo Occidental…

Justicia climática para África

Ante la catástrofe climática que acecha a África en el futuro próximo, más de 250 revistas científicas sanitarias, entre las que destacan The Lancet y The British Medical Journal, han publicado de forma simultánea un editorial en la que instan a los líderes mundiales a impartir justicia climática a dicho continente. Nunca antes tantas revistas científicas se habían organizado para lanzar un mensaje conjunto, con vistas a la Conferencia de las Naciones Unidas sobre el Cambio Climático (COP27). Este evento se está celebrando entre el 6 y el 18 de noviembre y será decisivo para que los dirigentes establezcan compromisos para mitigar el calentamiento global y establecer acciones para adaptarse y protegerse frente a este.

En el comunicado conjunto de las revistas sanitarias, los editores sostienen que dejar a los países a merced de los impactos medioambientales crea inestabilidad que tendrá, más temprano que tarde, graves consecuencias sobre todas las naciones: «La crisis climática es producto de la inacción global y conlleva un gran coste no solo a países africanos afectados de forma desproporcionada, sino también a todo el mundo. África está unida con otras regiones en primera línea para instar a las naciones ricas a dar, por fin, un paso adelante […]». 

El documento sostiene que las naciones en desarrollo no han recibido compensación por una crisis que no han provocado: «No es solo injusto, sino que también impulsa una espiral de desestabilización global, mientras los países destinan dinero a responder a los desastres, no pueden permitirse pagar una mayor resistencia o reducir la raíz del problema a través de las reducciones de las emisiones».

Los autores defienden la gran importancia mundial de cumplir con el objetivo, prometido en el Acuerdo de París de 2015, de destinar 100 mil millones de dólares cada año para financiar a los países en desarrollo frente a la crisis climática y evitar los riesgos sistémicos de dejarlos a su suerte. Esta financiación que, sostienen, debería ser en subvenciones y no en préstamos, se dirigiría a incrementar la resistencia de dichas naciones a los previsibles impactos del cambio climático y también como apoyo en los procesos de reducción de emisiones de gases invernadero.

Una combinación equilibrada entre la adaptación y la mitigación, en la que los sistemas sanitarios deben estar por delante, ya que las consecuencias de las crisis climáticas se manifiestan con frecuencia en problemas de salud agudos. «Financiar la adaptación será más costo-efectivo que centrarse en la ayuda de catástrofes».

El primer autor del comunicado, el profesor y decano de la Facultad de Medicina de África Oriental Lukoye Atwoli, declara que «Es la hora de que la comunidad global se dé cuenta de que la crisis climática, aunque afecte de forma desproporcionada al continente [africano], es una crisis global. Las acciones deben empezar ahora y hacerlo donde se está sufriendo más, en África. Fracasar en actuar hará que la crisis se convierta en el problema de todos muy pronto».

Para saber más:

Del cambio climático
Los ecosistemas acuáticos de África y el cambio climático
Lo prudente es hablar de emergencia climática

Sobre la autora: Esther Samper (Shora) es médica, doctora en Ingeniería Tisular Cardiovascular y divulgadora científica

El artículo Un llamamiento histórico para proteger África de la crisis climática se ha escrito en Cuaderno de Cultura Científica.

Sabemos muy bien cómo empujar a una criatura en el columpio del parque: podemos aumentar la amplitud de oscilación de la barquilla sincronizando nuestros empujones con la frecuencia natural de este péndulo. En física se puede fácilmente modelar esta dinámica mediante una sencilla ecuación diferencial y predecir cuál es la frecuencia de resonancia del columpio cargado. Dicho de otra manera: deducimos con exactitud a qué ritmo debemos empujar para que la oscilación del columpio se amplifique; y además sabemos que intentar empujar por encima o por debajo de la frecuencia de resonancia que hemos deducido es inútil, porque la oscilación del péndulo se atenuará. La caja de resonancia de un violín no es más que un columpio algo más complejo que el que acabamos de describir. Debido a sus características constructivas y mecánicas, la caja contiene decenas de frecuencias de resonancia en el rango de las vibraciones sonoras.

Foto: Roberto Delfanti / Unsplash

Sin una caja de resonancia en un violín, las vibraciones de sus cuerdas apenas son audibles. Así, la transmisión de las vibraciones de las cuerdas al cuerpo hace que tanto la caja como el volumen de aire de su interior empiecen a vibrar también. Debido a las frecuencias naturales de cada uno de los elementos del instrumento y a la unión de todos ellos en el violín, ciertas frecuencias y armónicos superiores de las ondas acústicas se amplifican o se atenúan en mayor o menor medida. De esta manera, se crea el carácter tonal individual de cada violín, que incluye el volumen y el timbre del sonido musical que este consigue.

La invención del violín moderno

La caja de resonancia de los violines fue mejorando a lo largo de los siglos. La lutería es tanto un arte como una ciencia, y todos los maestros artesanos constructores de instrumentos fueron desde sus inicios también científicos empíricos, capaces de aprender y avanzar en su área de conocimiento mediante continuos métodos experimentales de ciencia acústica, prueba y error.

El violín moderno fue construido en Europa a principios del siglo XVI. Entre las principales regiones europeas aspirantes al título de invención del violín están Füssen, en Algovia (hoy parte de Alemania), Sklenařice en la República Checa, Cracovia en Polonia, y, en Italia, Venecia, Brescia y Cremona. De todas ellas, fue Lombardía la cuna de los mejores lutieres, y más en concreto Brescia, con las violas encabezadas por Gasparo da Salò, y Cremona, con los violines representados por Andrea Amati. Este último es quien quizás pueda ser considerado el inventor del violín moderno, si debemos ceder semejante mérito a una única persona.

Árbol «genealógico» de la escuela de lutería de Cremona. Fuente Wikimedia Commons

 

Cómo medir el carácter tonal del violín

La acústica musical puede modelar el carácter tonal de un violín midiendo distintos parámetros importantes en la caja de resonancia. La forma más completa de caracterizar la calidad de un instrumento es medir la movilidad de su caja al recibir vibraciones de las cuerdas a través del puente.

La movilidad de la caja se denomina también admitancia mecánica (inverso de la impedancia mecánica) que se define como el cociente entre la velocidad que se produce y la fuerza que se aplica en un sistema mecánico. Para medir la respuesta en frecuencia de la movilidad de un violín, debemos ejercer sobre la caja una fuerza oscilante barriendo todas las frecuencias audibles, y medir las velocidades con las que responde dicha caja para cada una de estas frecuencias.

Con un computador se puede emitir un ruido blanco a través de una bobina que induce oscilaciones mecánicas a todas las frecuencias en el cuerpo del violín. A su vez, puede medirse con un acelerómetro la respuesta mecánica de la caja a todas estas frecuencias, y efectuar un cálculo de la transformada de Fourier y un gráfico en el dominio de la frecuencia de todo el mapa de resonancias del instrumento [1].

Método sencillo de medida del carácter tonal de un violín. Fuente: UPV/EHU, Dept Electricidad y Electrónica

 

Las resonancias del cuerpo de los violines pueden caracterizar la acústica de todo tipo de instrumentos, incluyendo piezas históricas de gran calidad musical fabricadas hace siglos por los grandes lutieres [2].

Ejemplo del espectro sonoro medido en un violín Fuente: Referencia [2]

 

Las medidas acústicas de la caja de un violín pueden distinguir varias resonancias de esencial importancia para el sonido que podemos extraer del instrumento. La cavidad del aire de la caja vibra a una frecuencia propia que podemos excitar fácilmente soplando por una de las aberturas acústicas en forma de f del violín y escuchar la nota que surge de la otra f. Otras resonancias de la caja debidas a la madera, espesores, curvas, geometría y construcción nos permiten completar el espectro sonoro del instrumento, así como su firma y carácter tonal.

Referencias:

[1] Victor Etxebarria and Iratxe Riera (2002) Measuring the frequency response of musical instruments with a PC-based system. Catgut Acoustical Society Journal, vol 4, n. 6, (Series II), pp. 26-30.

[2] F Leccese, G Salvadori, G Bernardini and P Bernardini (2018) The bowed string instruments: acoustic characterization of unique pieces from the Italian lutherie. IOP Conf. Series: Materials Science and Engineering vol. 364 pp: 012022

Sobre el autor: Victor Etxebarria Ecenarro está diplomado como lutier por el Conservatorio Juan Crisóstomo de Arriaga (Bilbao) y es Catedrático de Ingeniería de Sistemas y Automática en la Universidad del País Vasco (UPV/EHU)

El artículo La caja de resonancia del violín se ha escrito en Cuaderno de Cultura Científica.

¿Consideras que las moscas son criaturas “maravillosas”? ¿O que puedan tener un papel protagonista en la investigación contra enfermedades como el cáncer? ¿Alguna vez has llegado a reflexionar sobre la virginidad de estos insectos?

El investigador, doctor en Biología y profesor del departamento de Biología Celular de la Universidad de Sevilla Luis M. Escudero Cuadrado abordó estas cuestiones en su charla en Naukas Bilbao para responder que sí, que las tres son ciertas. ¿Por qué?

En primer lugar porque, aunque cueste trabajo creerlo, la mosca conocida como Drosophila melanogaster es muy parecida al ser humano. Tanto, que se utiliza para estudiar los procesos que llevan a la formación de nuestros órganos, hacer experimentos genéticos e intentar extraer conclusiones que resulten provechosas para la Humanidad. Para llevar a cabo estos experimentos los investigadores utilizan las moscas por varias razones: “Son pequeñas, manejables y tienen un ciclo de vida corto. En 10 días las moscas pasan del embrión a la larva y a la pupa; se produce la metamorfosis y tenemos nuevas moscas, y con una alta descendencia. Además, trabajar con ellas es barato”, explicó el científico.

Y es precisamente en este punto donde entra en juego la virtud de las hembras. Las moscas de este sexo tienen un órgano llamado espermateca que conserva un poco del esperma de cada uno de los machos con los que copula. Por eso, a la hora de garantizar que la información genética de las moscas no se vea alterada con el esperma de varios machos, es necesario que la hembra sea virgen e inducir la copulación en tubos de ensayo.

“Lo que hacemos es coger el tubo, dejar solo las pupas y esperar unas horas para que emerjan las nuevas moscas y tengamos así una guardería de vírgenes”, ilustró el investigador en lo que él mismo denominó “un curso completo de mamporrerismo de moscas en cuatro minutos”.

La finalidad de este “mamporrerismo” es encontrar genes que ayuden a descubrir aspectos que contribuyan a mejorar la vida del ser humano. ¿De qué manera? Luis M. Escudero se remontó a principios del siglo pasado, a los tiempos de Thomas H. Morgan, un genetista experto en investigación con moscas para responder a esta pregunta. Morgan quería resolver el enigma de la transmisión de la herencia genética entre generaciones cuando comenzó a cruzar una mosca con ojos blancos con otras con ojos rojos y se dio cuenta de que la información genética se hallaba en los cromosomas. Un hallazgo que le valió el Nobel de Medicina y Fisiología en 1933.

Morgan denominó white (blanco en inglés) a ese gen que daba la coloración blanca a los ojos de estos insectos, e inauguró la tradición de poner nombre a sus genes, hasta el punto de que hoy en día hay cientos de ellos. Por ejemplo, el gen tinman, que significa “hombre de hojalata”, es el que hace que se forme el corazón de forma correcta. Este gen tiene muchas similitudes con los genes humanos que participan en el proceso de formación del corazón.

Esta introducción permitió al investigador andaluz afirmar que la Drosophila es “maravillosa” ya que “las moscas han servido para investigar un montón de cosas que nos afectan, y para elaborar modelos de Alzheimer, Parkinson y cáncer”. ¿Cómo?

En concreto, el biólogo mencionó el ejemplo de un paciente con cáncer de colon a quien los tratamientos de cirugía, radioterapia y quimioterapia no le sirvieron para controlar la enfermedad e incluso comenzó a sufrir metástasis. Los investigadores identificaron los genes que estaban alterados en los tumores del paciente y crearon una serie de moscas con hasta ocho mutaciones diferentes que producían tumores muy parecidos a los suyos. Para intentar combatir estos tumores probaron en los insectos infinidad de combinaciones de compuestos hasta que dieron con una que conseguía que las moscas sobrevivieran. El resultado fue que después de 27 semanas de tratamiento el tamaño de las lesiones del paciente se redujo un 45%. Lamentablemente, el tratamiento se tuvo que suspender debido a un problema de efectos secundarios, pero abrió la puerta a nuevas investigaciones similares a las que se han desarrollado durante los últimos años.

Investigaciones como la que arrancó en La India hace 50 años con el descubrimiento de un gen, denominado wingless, que posibilita el crecimiento de las alas de una mosca han hecho que se avance muchísimo en la investigación biomédica. En aquella época la tasa de supervivencia en casos de cáncer de colon no superaba el 50%. “Ahora sabemos que los genes de esa familia están mutados en su gran mayoría de los tumores de colon”, explicó Escudero.

Los estudios de este tipo de genes en moscas, ratones y humanos han llevado a que hoy en día tengamos una tasa de supervivencia superior al 90% en este tipo de cáncer. El investigador concluyó su charla con un alegato optimista. “Trabajos como el que os acabo de comentar van a seguir aumentando esta estadística de cara a futuro. Seguro que sí”.

 



Si no ve correctamente el vídeo use este enlace.

Para saber más:

La inevitable ciencia de los bichos raros

Crónica de Roberto de la Calle / GUK

El artículo Naukas Bilbao 2022: La maravillosa labor investigadora de las moscas se ha escrito en Cuaderno de Cultura Científica.

La psilocibina es un alcaloide que una vez ingerido en el cuerpo se convierte en psilocina, un compuesto alucinógeno responsable del efecto psicoactivo de ciertos hongos comestibles. La psilocibina se encuentra en fases avanzadas de ensayos clínicos dirigidos al tratamiento de diferentes patologías psiquiátricas, tales como la depresión o las adicciones. Investigadores del grupo de neuropsicofarmacología de la UPV/EHU han estudiado en profundidad el mecanismo de acción de la psilocibina en ratones.

Psilocybe semilanceata. Fuente: Wikimedia Commons

La psilocibina se ha convertido en un fármaco potencialmente útil para varias enfermedades neuropsiquiátricas, presentando un inicio rápido de la actividad terapéutica. Sin embargo, los mecanismos responsables de tales efectos siguen siendo poco conocidos. El trabajo del grupo es relevante para comprender tanto el mecanismo de acción subyacente a los efectos terapéuticos como los potenciales efectos secundarios no deseados de esa sustancia psicodélica.

La psilocibina, naturalmente presente en algunas especies de hongos alucinógenos (hongos del género ‘Psilocybe’, entre otros), fue estudiada durante la década de los 60 para el tratamiento de diversos trastornos mentales, pero su uso y distribución quedaron prohibidos a partir de 1972. No obstante, en los últimos años, la comunidad científica ha retomado las investigaciones relacionadas con esa y otras sustancias de características similares, como el MDMA o el LSD.

Los ensayos clínicos desarrollados tanto en Europa como en América están dando resultados prometedores. “Esos estudios han sido el desencadenante para la descriminalización de la psilocibina y otros alucinógenos con potencial terapéutico en los Estados Unidos, lo que supone un avance para una futura aprobación para su uso clínico por las diferentes agencias reguladoras, principalmente la Food & Drug Administration (FDA) y la European Medicines Agency (EMA)”, explica Ines Erkizia, investigadora predoctoral del grupo y primera autora del artículo.

Los efectos agudos de la psilocibina y de su metabolito activo, psilocina, han sido ampliamente descritos tanto en entornos clínicos como por parte de usuarios en ambientes recreativos. Estos incluyen cambios en la percepción, como alucinaciones auditivas o visuales, y experiencias místicas o espirituales. Entre los efectos a largo plazo, los usuarios perciben cambios positivos en el humor y el estado de ánimo, lo cual podría suponer una mejora en la sintomatología de ciertas enfermedades psiquátricas. Los mecanismos que subyacen a esos efectos no son del todo conocidos, pero se han relacionado con incrementos de la plasticidad neuronal que parecen conllevar alteraciones en la conectividad de la corteza cerebral.

“Hemos confirmado un perfil farmacológico similar de psilocina en humanos y roedores -comenta la investigadora-. Además, se realizó un estudio farmacológico exhaustivo para identificar las dosis óptimas a utilizar en futuros estudios científicos de investigación básica y clínica. Nuestros hallazgos aportan datos valiosos sobre la implicación del sistema serotonérgico en los efectos de la psilocibina”, recalca Ines Erkizia.

Los resultados de esta investigación pueden proporcionar una nueva perspectiva sobre las dianas terapéuticas del fármaco para futuros estudios clínicos.

Para saber más:

Consumo de cannabis y desarrollo de esquizofrenia
Del metabolismo (y II)

Referencia:

I. Erkizia-Santamaría, R. Alles-Pascual, I. Horrillo, J.J. Meana, J.E. Ortega (2022) Serotonin 5-HT2A, 5-HT2C and 5-HT1A receptor involvement in the acute effects of psilocybin in mice. In vitro pharmacological profile and modulation of thermoregulation and head-twitch response Biomedicine & Pharmacotherapy doi: 10.1016/j.biopha.2022.113612

Edición realizada por César Tomé López a partir de materiales suministrados por UPV/EHU Komunikazioa

El artículo Los usos terapéuticos de la psilocibina de los hongos alucinógenos se ha escrito en Cuaderno de Cultura Científica.

Saltó a la fama gracias a The Doors y su sonido conquistó la música de finales de los 60 y principios de los 70. Se podía oír en todo tipo de música funk, rock y pop. Fue fundamental para el desarrollo del jazz-rock y de artistas como Miles Davis, Joe Zawinul, Chick Corea y Herbie Hancock. El piano Rhodes es ya un símbolo de toda una época. Lo que quizás no sabías es que en sus entrañas se encuentra la magia acústica del diapasón, y en sus orígenes, el horror de la guerra y bombarderos reciclados. Hoy te cuento su historia.

Viajemos hasta 1942. Europa se desangra bajo el peso de la Segunda Guerra Mundial, y han pasado pocos meses desde que Estados Unidos decidió enviar a sus soldados a la contienda. Entre las filas de estos recién llegados se encuentra un curioso personaje. Harold Rhodes ha sido reclutado para entrenarse como piloto de las fuerzas aéreas del ejército estadounidense1. Aunque todos le llaman oficial, él se define a sí mismo como profesor de piano —lo seguiría haciendo durante el resto de su vida—. Por eso, entre vuelo y vuelo, se dedica a dar clases de música a sus compañeros. Pronto, estas lecciones se vuelven tan populares, que el personal médico del ejército solicita su ayuda y Harold no se lo tiene que pensar dos veces. Equipado con su mejor arma, decide que su misión en medio del horror de la guerra será traer rehabilitación y consuelo a los soldados heridos, a través de la música.

Sin embargo, su tarea no era nada fácil. Para empezar, porque conseguir un piano para hacer musicoterapia de vanguardia no era precisamente una prioridad médica en medio de la Segunda Guerra Mundial —por lo que sea—. Pero además, muchos de los soldados que llegaban a sus manos se encontraban postrados en sus camas, sin posibilidad de moverse. Rhodes se vio forzado a inventar una nueva manera de impartir sus clases. En tiempos más felices, antes de la guerra, había puesto mucho empeño en enseñar a sus alumnos la mecánica de su instrumento, convencido de que entender el lenguaje de la música y cómo se produce el sonido era clave en su formación. Ahora, todo ese bagaje le ayudaría en su nuevo reto.

Rhodes se dispuso a crear un nuevo instrumento, un teclado portable y ligero, que los soldados pudieran tocar desde sus camillas, o sobre su regazo. Y ¿de dónde podía sacar el material necesario para construirlo? ¡De la propia guerra! Haciendo uso de su ingenio, decidió recurrir a una fuente insospechada de piezas de metal: aviones B-17 averiados. Las alas de estos bombarderos tenían unos tubos de aluminio que se podían cortar para crear láminas vibrantes de diferentes tonos. El “Xylette” —como llamó a su instrumento— tenía 29 teclas y era parecido a un xilófono, solo que con teclas. Una especie de piano de juguete. Y a pesar de ser bastante rudimentario, a los soldados les encantó. De hecho, el instrumento tuvo tanto éxito que Rhodes fue puesto a cargo del programa de rehabilitación de instrucción musical en todos los hospitales de la fuerza aérea. Se estima que el Xylette fue utilizado en hospitales de la Fuerza Aérea por miles de soldados.

El prepiano Rhodes (1950) es uno de los más antiguos, un modelo muy anterior al famoso piano eléctrico Fender Rhodes (1965). Fuente: Wikimedia Commons

 

Después de la guerra, Rhodes siguió trabajando en su idea. Como buen profesor de piano, su objetivo era llevar su nuevo teclado a las aulas, para seguir enseñando música. Así que se le ocurrió amplificar su sonido electrónicamente y adaptarlo para estudiantes. El “Pre-Piano” contaba incluso con un asiento adjunto, como una especie de pupitre sonoro. Una década más tarde, Rhodes se asoció con Leo Fender para desarrollar y fabricar el piano Fender Rhodes que hoy conocemos. El primer modelo fue lanzado en 1959 y contaba solo con el registro más grave. Fue el modelo que popularizó The Doors. Raymond Manzarek, el teclista, lo utilizaba en sustitución del tradicional bajo eléctrico. Poco más tarde, salió al mercado el primer teclado completo de 73 notas: el Fender Rhodes Mk1.

¿Pero cómo funciona exactamente este piano eléctrico? Bien, el mecanismo no es muy diferente al de un piano real, solo que, en lugar de cuerdas, tiene unas piezas de metal que vibran a distinta frecuencia. Cuando el martillo las golpea, su vibración es capturada por un transductor que convierte su energía acústica en una señal eléctrica, como sucede en una guitarra eléctrica.

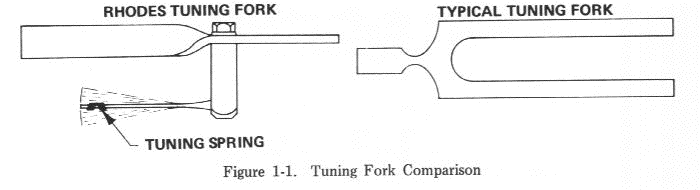
Pues bien, esas piezas de metal que sustituyen a las cuerdas son diapasones. ¡Sí, diapasones! Bueno, quizás un tipo de diapasón un tanto más asimétrico que el que solemos imaginar, pero instrumentos perfectamente equivalentes desde un punto de vista físico. En este caso, las patas de las varillas tienen distinta forma, masa y tamaño, pero son iguales en el tono. Y al igual que los diapasones, su sonido tiene propiedades especialmente interesantes para los músicos.

Piano Rhodes sin la tapa de forma que las piezas de metal (diapasones) quedan visibles. Fuente: Wikimedia Commons

De hecho, el piano de Rhodes resultó revolucionario en su época. Por primera vez en la historia, los teclistas podían llevar su propio piano portátil de viaje. Bueno, todo lo “portátil” que puede ser un piano, entiéndase. Nadie les libraba de cargarlo en una camioneta cada noche. Pero gracias a las propiedades del diapasón, el Rhodes apenas se desafinaba. Y como alternativa era mucho mejor, que el piano destartalado de turno que pudieran encontrarse en los clubes donde tocaban.

Pronto este instrumento conquistó el mundo del rock y de la música. A mí me cuesta oír su sonido sin que me venga a la cabeza de inmediato The Doors. Pero muchos otros artistas recurrieron a este piano electrónico, desde Herbie Hancock a los Beatles o Michael Jackson. No está nada mal para un piano de juguete fabricado con aviones reciclados.

Referencia:

1Elaine Woo, 2001. “Harold B. Rhodes; Inventor of Electric Piano”. Los Angeles Times. Consultado el 1 de noviembre de 2022.

Sobre la autora: Almudena M. Castro es pianista, licenciada en bellas artes, graduada en física y divulgadora científica

El artículo El piano que surgió de los restos de la guerra se ha escrito en Cuaderno de Cultura Científica.